将未知转化为已知，初悟运算的一致性

如何进行教学才能帮助学生感悟小数乘法运算的一致性呢？笔者团队开展了小数乘法单元教学，本节课是这个单元的第二课时。在前面的学习中，学生能够借助数位顺序表，感受并理解0.1×0.1及0.01×0.1的意义，明确小数乘法运算可能产生新的计数单位。在本节课中，首先，在回顾如何计算0.1×0.1的基础上，引发学生提出新的探索素材；其次，探索如何计算0.3×0.2，随后沟通不同方法之间的联系，进一步体会小数乘小数的意义，感受计算就是计数单位的累加，从而感悟计数单位和计数单位个数的作用。

一、在回顾如何计算0.1×0.1的基础上，引发新的探索素材

1.借助面积模型，回顾0.1×0.1=0.01。

师：上节课我们研究了0.1×0.1=0.01， 0.1×0.1是怎么得出0.01的？谁来说说自己的想法？

师：过程说得非常清楚，那我们一起通过看图回顾一下这个过程（如图1）。

在这一活动中，学生能够借助正方形面积模型进行说理，得到0.1×0.1=0.01。不仅初步建立了小数乘小数的意义，更突出了0.1×0.1这一计数单位的运算及其产生了新的计数单位，为后续的学习奠定了基础。

2.鼓励自主学习，得出新的探索素材。

教师启发学生思考：在研究了0.1×0.1=0.01之后，还能计算哪些小数乘小数的算式？学生得出要继续研究的小数乘小数的新算式，并将自己写出的算式贴在黑板上（图略）。

在此基础上，教师带领学生按照小数位数把黑板上的算式进行分类：一位小数乘一位小数、一位小数乘两位小数、两位小数乘两位小数，其余的算式分到其他类中。在讨论中，学生确定了先从位数最少的“一位小数乘一位小数”开始研究，选择了0.3×0.2作为研究的起点。

【设计意图】通过直观的面积模型，借助小数的意义和小数乘法帮助学生回顾0.1×0.1 的算理与算法。在教师的引领下，学生自由写算式，并将算式进行分类，确定了本节课的研究起点，这一过程为加深对小数乘法运算意义的理解奠定了基础。

二、探究如何计算0.3×0.2，将未知转化为已知

教师鼓励学生借助学习单自主探索计算0.3×0.2，在画一画、写一写的探究过程中，让学生把思考过程表达清楚。在学生独立思考后，教师利用实物投影展示学生的多种思考方法。

随后，学生进行小组合作学习，解读多种方法背后的算理，从而引发新的思考，并在全班共同理解各种方法。

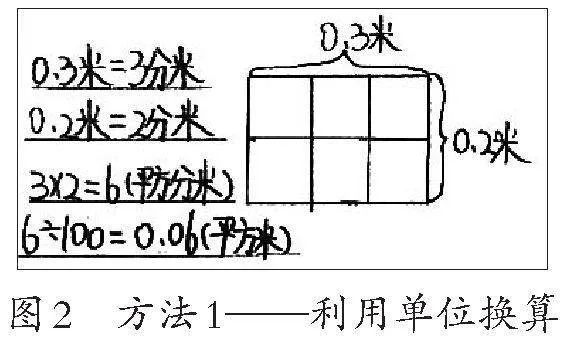
方法1：利用单位换算（如图2）。把0.3看成0.3米，把0.2看成0.2米。将0.3米换算成3分米，0.2米换算成2分米，长方形的面积就是3×2=6（平方分米）。因为平方分米和平方米之间的进率是100，所以6÷100=0.06（平方米），即6平方分米=0.06平方米。

方法2：利用积的变化规律（如图3）。先把0.3看成0.3×10=3，再把0.2看成0.2×10=2，3×2=6，因为0.3和0.2都扩大到原来的10倍，所以0.3×0.2的结果扩大到原来的10×10，也就是100倍，所以需要把6缩小到它的百分之一，也就是除以100得到最后的结果是0.06。

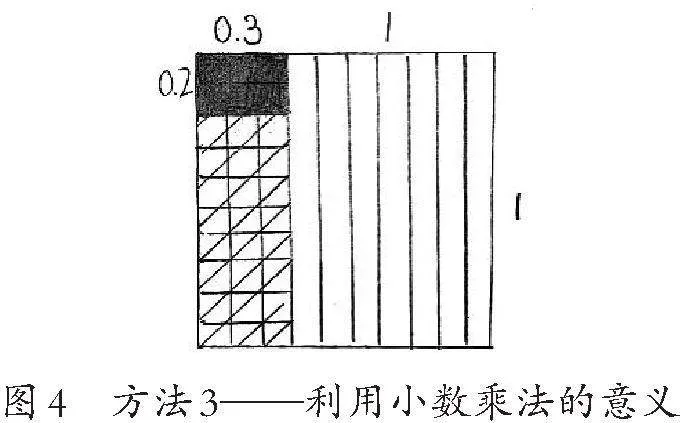
方法3：利用对小数乘法意义的理解（如图4）。把1平均分成10份，取其中的3份，也就是0.3。因为0.3还要再乘0.2，也就是把0.3再平均分成10份，取其中的2份，就是0.06。

师：你能从图中找出0.2、0.3与0.06吗？

学生继续观察面积模型图，从图中找出表示0.2、0.3、0.06的部分。

生1：把1平均分成10份，其中的3份也就是这3条是0.3。再把这3条平均分成10份，取其中的2份，就是0.3×0.2。

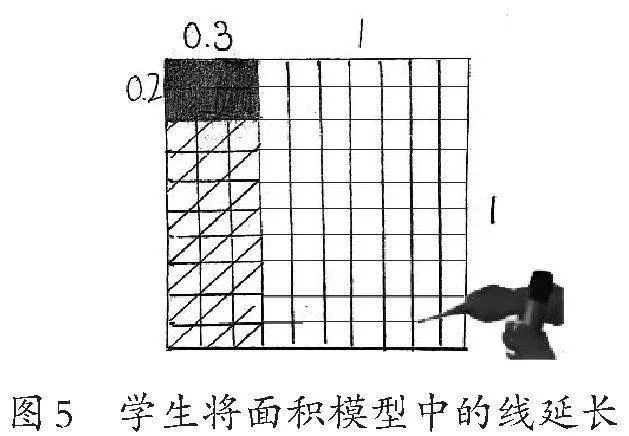
师：怎样能更加清楚、直观地从图中看出整体与部分之间的关系呢？

生2：我们应该把线延长，这样会看得更加清楚。

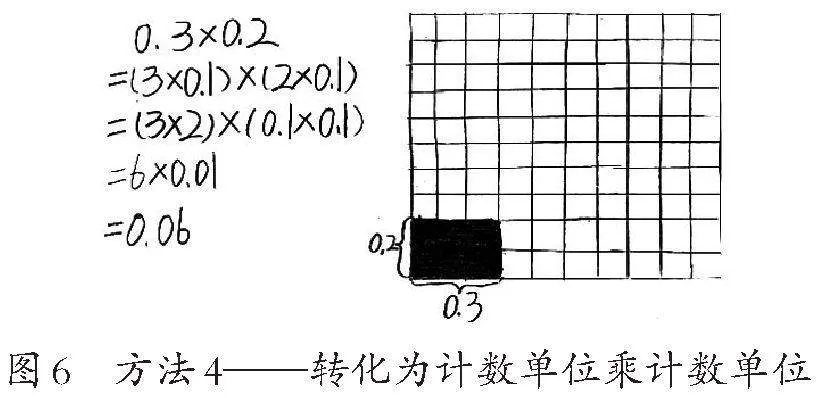
方法4：转化为计数单位乘计数单位（如图6）。把0.3看成3×0.1，把0.2看成2×0.1，再算（3×2）×（0.1×0.1），也就是6×0.01，可得结果是0.06。

这种方法激发了学生的思考意识，他们积极参与到方法解读的过程中来。

生1：0.3和0.2的计数单位都是0.1，所以可以把0.3拆成3个0.1，0.2拆成2个0.1。

生2：用计数单位的个数乘计数单位的个数，再乘“计数单位×计数单位”，就得到6个新的计数单位0.01。

师：这正是我们上节课研究过的，0.1×0.1会得到新的计数单位0.01。

【设计意图】教师给予学生充足的时间和空间，学生在经历自主计算、探究交流、表达想法的过程中，感悟将未知转化为已知，发展运算能力和推理意识。同时，鼓励学生解读不同算法，这有利于学生更加深入地理解算理，初步体会方法之间的联系。

三、沟通不同方法之间的联系，感悟一致性

教师鼓励学生进一步寻找这些方法之间的联系。

师：大家从不同角度思考，用不同的方法，都计算出了0.3×0.2=0.06。请大家再想一想，这些方法有没有相同的地方呢？

学生认真思考后，开始了交流。

生1：我发现这些方法中都有6，都除以了100。

生2：从正方形图上可以看出来平均分成了100份，我理解的是除以100，但是最后一个是乘0.01，没有除以100啊。

师：敢于提出疑问，真好！谁能回答这个问题？

生3：0.01是百分之一，而除以100就是把1个整体平均分成100份，其中的1份是百分之一，也就是0.01。我认为“÷100”和“×0.01”样子不一样，但表达的意思是一样的。

师：说得真清楚，看似不同的方法中还真有相同的地方呢，都有“6”，都有“÷100”，也可以说都有“×0.01”。继续深入思考，大家还有什么问题吗？

生4：怎么都有“6”？怎么都有“÷100”或“×0.01”？

师：问得好！请大家静静地观察、思考。（停下来，给学生思考的时间和空间）谁来说说自己的想法？

生5：我发现了，无论什么方法，都是在解决“0.3×0.2”，都是3个单位乘2个单位，也就是3个2或者2个3，所有的方法都有6个最后的单位，也就是6个0.01，所以都有6÷100或6×0.01。

通过寻找不同方法的相同点，学生体会背后相同的算理，感悟运算的一致性。在此基础上，教师鼓励学生再选一道题进行计算。

学生选择了0.9×0.3，独立思考后开展全班交流，大多数学生利用积的变化规律、转化为计数单位乘计数单位进行计算并说理，在交流方法中继续沟通方法之间的联系。

最后，教师鼓励学生利用今天学习的方法，自主挑选黑板上的算式继续推理计算，将其作为课后作业。

【设计意图】在呈现0.3×0.2多种计算方法的基础上启发学生比较，发现不同方法的相同之处，体会“6”和“÷100”（或“×0.01”）的意思，感悟运算的一致性。通过相似题目的运算及分享，再次感悟算法背后算理的一致性。

本节课在研究0.1×0.1的基础上，从学生自主写算式、挑选研究素材入手，为学生的研究提供了路径。在自主研究0.3×0.2的过程中，教师给学生足够的时间和开放的空间，鼓励学生自己解决问题，在对比建立联系中感受不同方法之间的联系。

值得一提的是，在探索0.3×0.2的过程中，学生对乘法运算产生了浓厚的兴趣，愿意进一步研究是否所有的小数乘法运算问题都可以解决。可以说，学生的这种探索欲、不断思考下去的力量，正是我们所期望达成的学习愿景！