凸显计数单位，感悟运算的一致性

“乘法回头看”是在六年级总复习阶段开展乘法运算一致性教学的一次尝试。本节课从意义、算理和算法角度进行乘法运算的整体回头看。

一是运算意义角度。现行教学中，对于整数乘整数，从相同加数的和或倍的角度理解其意义；到了小数乘小数，并没有经历意义的学习，直接进入算理、算法的探究；对于分数乘分数，则在相同加数的和的基础上，从一个数的几分之几的角度进行理解。因此，有必要对意义进行回顾，让学生认识到无论整数乘法、小数乘法还是分数乘法，都可以从“相同加数的和”或“一个数的多少倍”理解其意义。

二是算理和算法角度。对于小数乘法和分数乘法，是从不同的角度进行算法探究的（对于小数乘法，将其转化成整数乘法，进而总结出算法；对于分数乘法，则基于意义通过画图实现算法的探究），但都可以看成“计数单位与计数单位相乘得到新的计数单位，计数单位的个数与计数单位的个数相乘得到新计数单位的个数”。

通过“回头看”，帮助学生感悟乘法运算的一致性，体会知识之间的联系。

一、预学反馈，理解乘法意义的一致性

在课前，教师布置了“以20×30、0.2×0.3、

在建立三类乘法意义之间的联系时，有的学生从不同的角度分别阐述整数、小数、分数乘法的意义（如图1）；有的学生则尝试从“几个几”或“几倍”的角度阐述三类乘法的意义（如图2）。

在寻找三类乘法算理、算法之间的联系时，多数学生能够借助直观图讲述乘法的算理，部分学生意识到三类乘法“都在算2×3”（如图3），并且在寻找的过程中，有的学生对算法与算理之间的联系表现出了一定的好奇。

同时，在学生的自主梳理中也存在一些值得关注的问题，如学生的表现水平不一、对算理和算法的一致性还需进一步探讨、对算法与算理之间的联系表现出一定的好奇等，这些问题的解决有助于学生感悟乘法运算的一致性。

在学生自主梳理的基础上，课始，教师组织学生针对三类乘法的意义进行小组讨论，互相启发，在组内达成初步共识后，进行全班交流。

师：这三类乘法在意义上有怎样的联系呢？谁来说说自己的想法？

师：从倍的角度理解这三类乘法的意义，大家可以接受吗？

生：可以接受，倍可以是整数倍，也可以是小数倍，如谁是谁的1.5倍。

生：我认为也可以是分数倍。

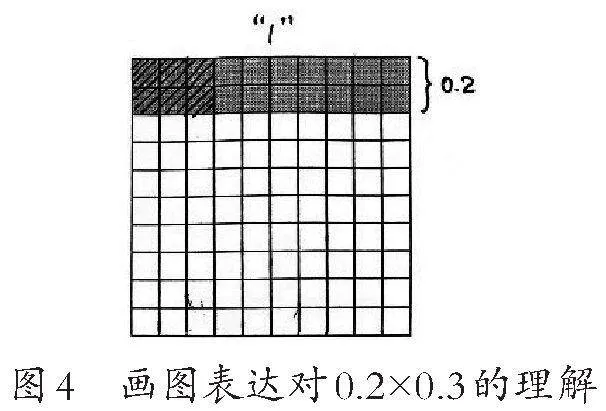
生：0.3个0.2就是在这个“1”中，先取它的0.2，也就是把这个正方形平均分成10份，取其中的2份；然后在这个0.2中再取它的0.3，也就是把0.2再平均分成10份，取其中的3份（如图4）。

生：我觉得你这样解释不是在说0.3个0.2，而是在说0.2的0.3是多少。应该先找到0.2，0.3个0.2是不够1个0.2的，把0.2平均分成10份，取其中的3份，就是0.3个0.2了。

其他学生点头表示赞同。

师：看来，小数乘法的意义可以理解成相同加数的和，也可以理解为一个数的多少倍。

【设计意图】以三个例子为媒介，回顾它们的意义，发现三类乘法在意义上的共同之处。其中整数乘法的意义最易理解，是理解其他乘法运算意义的基础；对于小数乘法的意义，需要将其转化成分数，借助分数的意义理解。在现行教学中，小数乘法的意义学生并没有讨论过，因此这个环节的关键是理解“0.3个0.2”是什么意思，鼓励学生借助画图，通过分数的意义加以理解。

二、交流提升，理解算理、算法的一致性

理解算理、算法的一致性是本节课的核心内容，法离不开理，理支撑着法，二者密不可分。在组内交流的基础上进行全班反馈，共同探讨这三类乘法在算理、算法上的联系。

1.阐述算法背后的算理。

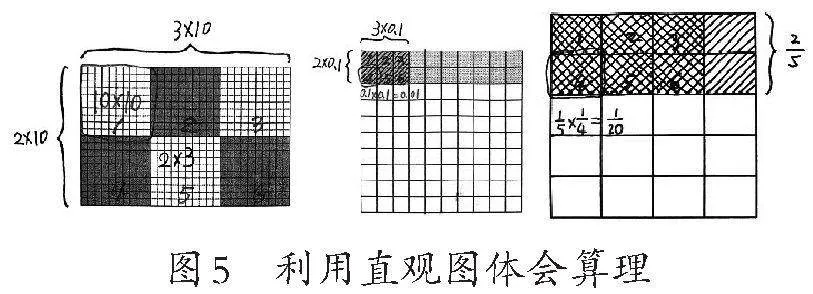
在回顾算法后，学生借助直观图讲述三类乘法算法背后的算理（如图5）。通过在直观图上进行圈画，发现三类乘法都是在计算6个格子有多大，区别在于格子的大小是不同的。在讨论中全班逐步达成共识，为理解算理的一致性做好铺垫。

生：20表示2个十，30表示3个十，2乘3算的是共有6个大方格，每个大方格都是10乘10共100个小方格，也就是6乘100，结果就是600。

生：把大正方形看作“1”，平均分成10行，每行是0.1，2个0.1就是0.2；再平均分成10列，取其中的3列，0.2×0.3计算的就是这6个格子的大小，每个格子都是0.1×0.1=0.01，所以结果是0.06。

2.感悟计数单位的作用。

师：如果用算式把整数乘法的算理记录下来，应该怎么做呢？

教师边引导讨论边在黑板上板书：（2×10）×（3×10）=（2×3）×（10×10）=6×100。

学生板演（如图6）：

师：好好观察这三个横式，想一想，它们的第一步都是怎么得到的呢？

生：把每个数都写成了“几×计数单位”的形式。

师：是的，我们所学的整数、小数和分数都离不开计数单位。从第一步得到第二步，是什么在支撑着我们这样做？

生：是乘法的交换律和结合律。

师：谁来解释一下整数乘法的算式？

生：20表示2个十，30表示3个十，我们之所以在2×3的结果，也就是6的后面添上2个0，是因为10×10会得到新的计数单位——百。

随着学生的回答，教师运用板书帮助他们理解，如图7。

师：谁能也像这样，连一连线来说一说小数乘法和分数乘法计算的道理？

学生板演（图略）。通过连线，学生将竖式与横式建立联系，即建立算法与算理之间的关联，感悟法是理之显，理是法之源。

师：你们发现三类乘法之间的共同点了吗？

同伴进行交流，然后全班反馈。

生：我发现无论整数乘法、小数乘法还是分数乘法，都在计算计数单位乘计数单位得到的新计数单位是多少，以及个数乘个数得到的新计数单位的个数是几。

师：原来看似不同的乘法，其背后蕴含的道理是一致的，都要先确定计数单位×计数单位得到的新计数单位是多少，再通过个数×个数得到新计数单位的个数。

【设计意图】这个环节重点解决两个问题：（1）以横式表达算理，通过纵向对比，发现乘法算理的一致性；（2）横向观察，进一步理解“法蕴含理，理支撑法”，以及运算律的重要作用。

三、拓展延伸，在理解的基础上展开联想

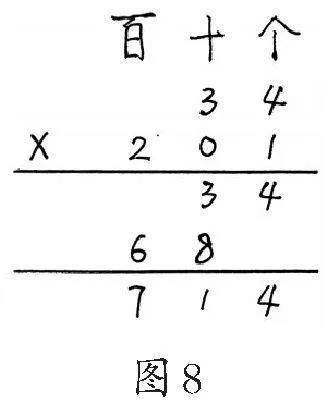
教师呈现一个整数乘法典型的竖式错例（如图8），借助计数单位帮助学生辨析错因并加以改正。

在此基础上，教师提供香港一本教材中的小数乘法竖式（如图9），请学生讲述这样写竖式的道理，将竖式补充完整，并寻找这个竖式与我们熟悉的竖式之间的相同点与不同点。

生：我们的竖式是先算数量，然后把数量加起来，最后看计数单位是多少。而这个竖式是先看计数单位，最后把数量加起来，做到了数位对齐。无论怎么算，都要注意结果的计数单位是多少，有多少个计数单位。

在此基础上，教师鼓励学生畅谈收获，展开联想。

师：这节课我们一起回顾了曾经学过的三类乘法，你有哪些收获？

生：我知道了所有乘法的结果都是有联系的。

生：通过这节课，我真正理解了为什么要这样算，而不是单单算出来。

生：我知道了计数单位乘计数单位会得到新的计数单位。

生：我知道了我们的竖式为什么要这样写。

师：通过这节课的学习，你是否联想到一些新的问题？

生：整数乘法、小数乘法和分数乘法都是在算新计数单位是多少，以及有多少个新计数单位，我提出的新问题是：除法是不是也是这样的呢？

生：我们以后可能还会学习其他数的乘法，是不是也离不开计数单位和计数单位的个数呢？

【设计意图】通过表述这个“不同以往”的竖式的算理，再次巩固对算理、算法一致性的理解，并将这个竖式与现行教材中的竖式进行对比，发现现行教材中的竖式“先按整数算出积，再来确定小数点的位置”的算法背后，蕴含着“先计算新计数单位的个数，再用个数乘新计数单位”的道理。在学生总结这节课的收获之后，提出“是否联想到一些新的问题”的数学思考，目的是帮助学生打开思路，从整数乘法、小数乘法、分数乘法这三类乘法的圈子里跳出来，将思考迁移到全新领域中。