“做”中识形，“思”中解义，“画”中悟法

“平行四边形的特征”是“图形与几何”领域的内容，“图形与几何”在小学阶段包括“图形的认识与测量”和“图形的位置与运动”两个主题。2022年版课标将认识和测量放在一起，其实表明了两者之间密切的关系，它们共同承载着发展学生的空间观念、几何直观、量感、抽象能力和推理能力的作用。图形的认识聚焦的是图形的特征，认识图形的特征大致可以从图形的要素特征、测量特征和关系特征三方面展开。

史宁中教授指出图形（平面图形和立体图形）都是从生活实物中抽象出来的，马云鹏教授指出图形认识的本质是抽象。图形抽象的第一步是描绘物体的外部形象，其核心是把三维空间的物体用线条描绘在二维平面上；第二步是图形表达的符号化和论证过程的形式化。在小学具体教学中可以把两位教授的语言转化为两次思维飞跃，即从实物抽象出几何图形，再由几何图形抽象出概念。

基于以上分析，我对“平行四边形的特征”一课进行了设计。本文以课前调研和“做”“思”“画”为主线，聚焦学生核心素养发展，阐述我的设计思考。

一、课前调研，有的放矢

学生在一年级时已经初步认识了平行四边形，在众多几何图形中能够辨认出平行四边形，三年级通过观察和操作进一步认识了长方形、正方形的特征，有了一些研究图形特征的经验，本节课通过观察操作进一步认识平行四边形的特征，为后续学习平行四边形的面积、初中学习平行四边形的判定定理和性质定理奠定基础。

为了有针对性地进行设计，课前对学生进行了学情调研。

调研题目：

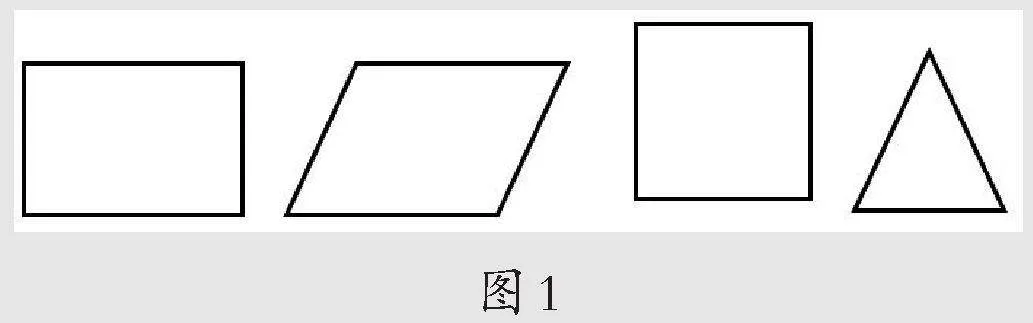
1.下面的图形（如图1）中哪个是平行四边形？

2.请你在方格纸上画一个平行四边形。

3.请你在白纸上画一个平行四边形。

第1题是辨认图形，调研结果显示正确率为100%，说明学生能够正确辨认平行四边形。第2题和第3题是从不同层次画图形，正确率分别为90%和60%，从学生绘制平行四边形的笔迹上看，有擦擦改改的痕迹，说明学生可以通过不断调整，使图形逐渐趋近于头脑中对平行四边形的直观印象。

课前调研结果显示，学生能够正确辨认平行四边形。于是，本课选择开门见山，导入新课。从实物中抽象出几何图形，完成学生思维的第一次飞跃。（如图2）

二、充分“放手”，“做”中识形

既然学生对于平行四边形的认知并非一张白纸，那么本课就改变研究方式，将平行四边形的特征的探究空间和时间交给学生。

教学片段一：

师：你用手里的学具做出平行四边形了吗？你是怎样做的？有什么发现？

生1：我用钉子板和橡皮筋围成了平行四边形，上面围4个钉子，下面往左倾斜一些也围4个钉子，围成的就是平行四边形。（同学们全部认可围成的图形是平行四边形）

师：通过围，你认为平行四边形有什么特征？

生1：平行四边形对边是相等的，你看上下这组对边都围了4个钉子，左右这组对边都围了3个钉子，只有保证上下和左右相对的钉子数是一样的，才能围出平行四边形的样子，所以我想平行四边形的对边是相等的。

生2：我还发现平行四边形的对边是平行的，因为钉子板上的钉子每一行都是平行的，所以我们围的时候平行四边形的对边也是互相平行的。

同样的，学生利用方格纸、可拼插的小棒等都制作出了不同的平行四边形实物，在制作的过程中学生就将头脑中对平行四边形特征的表象慢慢升华成对特征的理解。

教学片段二：

学生用小棒拼平行四边形没有成功。

师：为什么你们组没有拼出平行四边形？

生1：因为我们组的小棒是2根红的，1根黄的，1根蓝的，没法拼成平行四边形，拼平行四边形需要两组长度相等的小棒。

师：那你们需要1根什么小棒？

生1：我们需要1根黄的，或者1根蓝色的。

教师提供1根黄色小棒，学生用2根红色和2根黄色的小棒进行拼插，在拼插的过程中学生把2根黄色连在了一起，多次拆开调整依然没有拼出平行四边形。

师：需要帮助吗？

生1：需要。

师：谁来帮帮他？

生2：你把2根黄色的连在一起了，它们需要放在对面，不能连在一起。

生1进行调整，拼出了平行四边形。

师：回顾刚才的研究过程，你们组为什么没有拼出平行四边形？

生1：因为我们没有两组相同长度的小棒。

师：看来拼平行四边形需要两组长度相等的小棒，也就是说平行四边形有两组长度相等的边。可是为什么给了你两组长度相等的小棒还是没有拼出平行四边形呢？

生1：平行四边形不仅有两组长度相等的边，相等的边还要是相对的，不能相邻。

师：说得真好，你看我们错着错着就对了，我们对平行四边形的特征理解得更透彻了，平行四边形的两组对边分别相等。

【思考】小学的几何不是论证几何，更多的是属于直观几何、操作几何，学生获得几何知识并形成空间观念，更多的是依靠他们的动手操作，即在做中学。

以往授课教师给出了圆形纸片等现成的研究材料，让学生通过折一折、量一量等研究平行四边形的特征，此次授课我把现成的研究材料换成了钉子板、可拼插的小棒、网格纸和白纸，让学生利用已有知识和经验动手制作平行四边形学具。这一设计并不是单纯追求一个“变”，而是建立在调研和理解教材的基础上，这样的设计让学生换了一种方式来获取知识，学生在“做”中感悟、在“做”中思考，在调整学具的过程中为平行四边形“画像”，把课堂真正还给学生，促进学生发展。

四样研究材料可以从不同角度和层次帮助学生认识平行四边形的特征。事实证明，学生根据已有知识和经验能够制作出平行四边形。学生在选取材料拼插和绘制的过程中就会有发现，在调整中必然有思考，在议论中就会有提升，在“做”中完成平行四边形的“画像”。

三、对话想象，“思”中解义

教学片段三：

师：用你自己的话说一说，什么样的图形是平行四边形呢？

生1：两组对边分别平行、两组对边分别相等、对角相等的四边形就是平行四边形。

师：你们都同意吗？（学生全部同意）请同学们翻开书看看书中是怎样说的。

生2：两组对边分别平行的四边形就是平行四边形。

师：为什么书中只用到平行四边形的一个特征就下定义了呢？请你想象一下，这样行不行？换句话说，两组对边分别平行的四边形是不是平行四边形？

生：（举出反例）长方形、正方形两组对边分别平行，它们不是平行四边形。

师：同学们用找反例的方式进行研究，非常好！那么长方形、正方形是不是平行四边形呢？

课堂顺着学生的疑问，先进行长方形、正方形是不是平行四边形的探究，探究后学生肯定：长方形、正方形是特殊的平行四边形。

生2：我想，两组对边分别平行，那个平行的两条边夹的那两条线段就相等，两组平行线互相夹的都相等，所以两组对边分别平行了，对边就一定相等，对角也就相等了。所以下定义时只要说一条就行了。

生3：我同意生2的，我补充，因为两组对边分别平行了，如果对边不相等，那个边就裂开了，肯定就不平行，也就是说两组对边分别平行，对边就一定会相等。对角也就一定相等。

生4：我没有找到反例，于是我就思考，两组对边分别平行好像就保证了两组对边分别相等、对角也相等。所以好像用一个特征能够定义平行四边形。

此时教师拿出两组平行线利用方格纸进行演示，让学生直观感受两组对边分别平行了，所夹的对边就是相等的，对角也相等。

【思考】学生在充分地动手操作和沟通交流后，总结出了平行四边形的特征——两组对边分别平行、两组对边分别相等、对角相等。至此学生完成了从图形中抽象出特征的过程。从特征到概念是学生理解起来非常困难的地方。

查阅了多个版本的教材，大多数没有对平行四边形下定义。我是否可以选择对概念避而不谈呢？避而不谈就不能让学生体会到概念的概括和简洁的特点，何况学生初中会继续学习平行四边形的判定定理，这些定理都只用到了平行四边形中的一个或一组特征，放眼学生的未来，概念一定要研究。

从图形中抽象出概念，这是学生思维的第二次飞跃。无疑概念的教学需要学生有十足的想象力，这对小学生来说是一个挑战。教师在此给了学生充分的想象空间，学生在想象的过程中不仅完成了对于概念的认知，更能够培养学生的空间观念，想象是“图形与几何”领域培养学生空间观念的重要手段。

四、动手实践，“画”中悟法

教学片段四：

师：图4中的AB、BC分别是平行四边形相邻的两条边，请你接着把这个平行四边形画完整。

师：你是怎样画的呢？

生1：我利用两组对边分别平行的特征画出了平行四边形。

师：他利用定义画出了平行四边形。

生2：我先画出BC的平行线，再量出与BC相等的长度6厘米，得到平行四边形的顶点D，然后连接点C和点D就画出了平行四边形。

师：这位同学运用了一组对边平行且相等画出了平行四边形。

生3：我分别量出BC的长度和AB的长度，然后画出AD与BC相等，CD与AB相等，这样就画出了平行四边形。

师：这位同学利用两组对边分别相等画出平行四边形，这样画理论上没有问题，但在操作中会不会出现问题呢？

生4：这样画，如果AD斜了一些不与BC平行了，那么CD的长度就不等于AB了，就不是平行四边形了。

师：同学们想象一下，是这样吗？我们需要找到那个点D，正好让AD等于BC的长，CD还要等于AB的长，你们能想象怎样找到那个点吗？

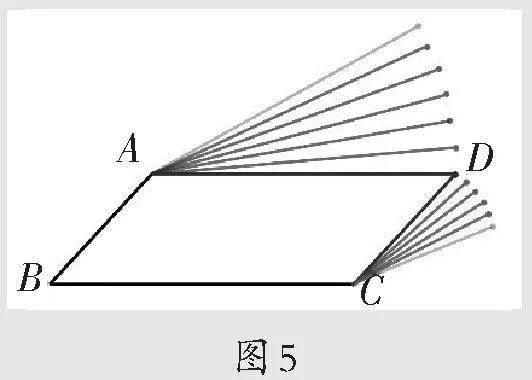
在学生充分想象后，教师借助动画让学生感受找点的过程，在这一过程中，想象能够帮助学生更深刻地理解特征，同时让学生对尺规作图有一个初步的感悟，明白尺规作图背后的道理。（如图5）

【思考】学以致用是解决问题的永恒话题。本课的最后，我让学生利用平行四边形的特征完成补画平行四边形的任务。教师没有教给学生怎样画平行四边形，而是让学生主动运用平行四边形的特征进行绘制，学生画平行四边形的过程不仅仅是对于特征的深化理解过程，实际上学生也对特征进行再加工的过程。

学生的画法依据“两组对边分别平行”“一组对边平行且相等”“两组对边分别相等”，这些正是平行四边形的定义和判断定理，此时学生的感悟可以帮助学生未来更好地理解知识，教师的放手成就了学生更多元的发展。

总之，本堂课教师改善了研究方式，能放手时就充分地放手，学生在“做”中完成了对图形的初步画像，在思考、交流中明晰了概念，在“画”中深化了对图形特征的理解，所有的任务最终成就的是学生思维的深度发展，学生的核心素养得到提升。