这样算真简便吗

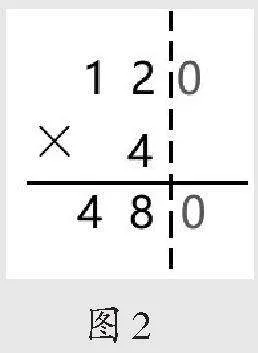
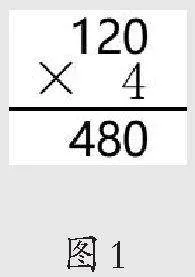
最近听了三节“乘数末尾有0的三位数乘一位数的笔算”，在尝试计算、阐述算理环节，对于4×120，学生出现了三种算法：12×4=48，120×4=480；（记为方法1）竖式计算；（如图1，记为方法2）20×4=80，100×4=400，400+80=480。（记为方法3）在交流算理之后，三位教师不约而同地问：“还有别的竖式计算方法吗？”学生没有回答，然后教师边示范边说明图2所示的方法。（记为方法4）为了区分和突出0，还用红颜色的粉笔做了强调。随后让学生进行方法对比，看哪种最简便。学生很“明智”地选择了方法4！课间和学生交流时，有学生说出了内心的想法：方法1是最简便的，它其实与计算30×2的思路是一样的，不用列竖式，甚至能口算，方法4是最麻烦的，要列竖式，还要画虚线，甚至要用红笔把0描出来。

大部分教师都默认方法4是解决这类计算题的简便算法，事实上这种方法只是“竖式的简便写法”或“简便算法的竖式写法”。

那么，该如何调整呢？首先，应规范名称，以免误导。其次，比较的聚焦点一是几种方法在算理上的一致性，二是两种竖式计算方法的差异，突出图2所示的竖式的简便之处。大致的环节可以这样设计：

1.在学生交流了方法1到方法3后，可以先让学生说说方法2对应的具体计算步骤，再让学生比较方法2和方法3，他们发现两种算法的算理和过程是相似的，只是形式上有差异。

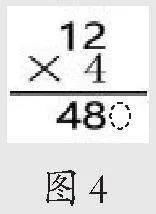
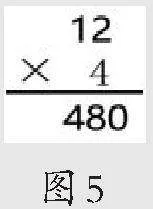
2.让学生用竖式展现方法1对应的过程。学生可能会得出以下几种竖式。（如图3～图5）教师引导学生发现这几种竖式在算理和算法上是一致的，只是表达形式上有差异。

3.让学生比较两种竖式（如图1和图3）的差异。学生发现图3所示的是转化成两位数乘一位数，图1所示的是三位数乘一位数，图3所示的竖式计算步骤要少一些。

如此调整，主要是引导学生剖析几种算法算理的一致性，帮助学生深度建构算法、理解算理。