从结果的不同到意义的一致性

[案例描述：]

最近，在开展四年级数学教研活动中，教研员说了四年级上册教辅材料上的一道连除计算题：“708÷3÷6=？”这有什么难度吗？我不以为然，快速算出了708÷3÷6=236÷6=39……2。没有想到，除了我说的答案，别的老师还说出了另外两种结果：708÷3÷6=39……1；708÷3÷6=39……6。由于苏教版教材四年级上册第四单元才系统地学习脱式计算，教辅材料的编写者根据教学的进度，对于此题只要求学生直接写得数。但学生的计算结果和我们老师一样出现了三种情况。对于哪一种是合理的，老师们给出了不同的看法。部分老师认为：708÷3÷6=236÷6=39……2是按照教材上给出的运算顺序进行计算的，结果肯定是正确的，而708÷3÷6=708÷18=39……6和708÷3÷6=118÷3=39……1这两种算法，由于改变了运算顺序，结果肯定是错误的。

[案例分析：]

1.寻找支撑学生不同计算方法的依据。

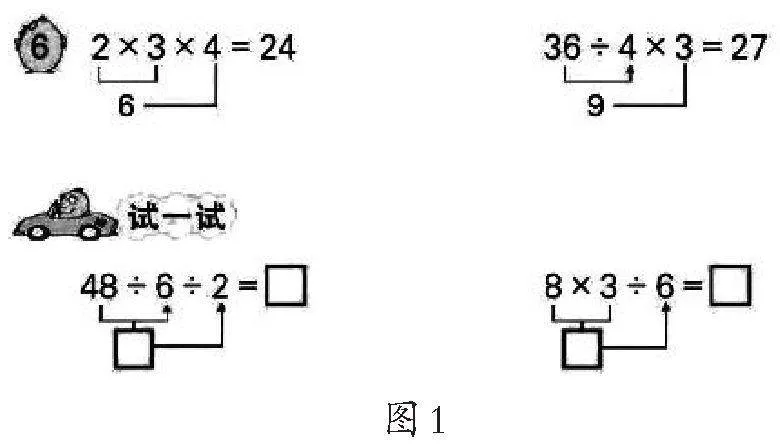
茫然之余，我选择从“根”上去解决。连除计算题是在二年级上册第六单元例6下面的“试一试”中首次出现的。（如图1）从图示中可以看出，编者的意图是让学生体会“同级运算”按照从左到右的运算顺序来计算。但这并不能帮助学生理解程序，相反，经验告诉他们：连加、连减、连乘和连除运算是可以改变运算顺序的，这种经验会迁移过来，而且经过多次做题，验证了这样运算是对的！

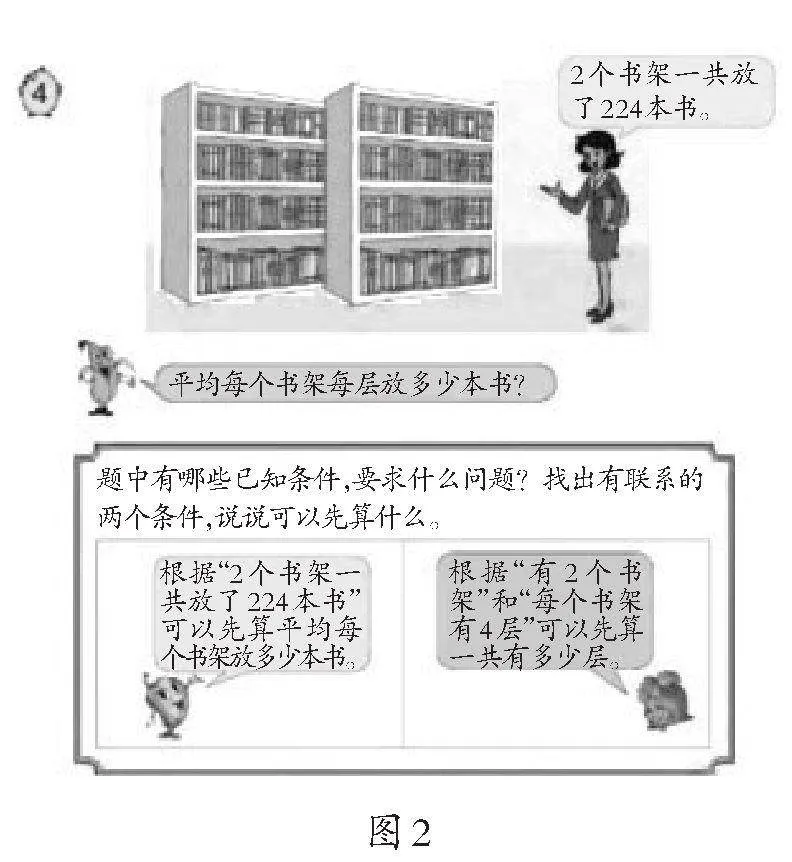
关于这一块的内容，苏教版教材原来安排在三年级下册第一单元，但不让学生列综合算式。改版后的教材把这一内容安排在四年级上册第二单元，为了帮助学生理解每一步计算的意义，明确运算顺序规定的合理性，教材例题提供了这样的生活情境图。（如图2）教材没有要求直接列综合算式，而是先让学生结合情境图理解两种分步列式的思路，计算出结果后，再根据分步算式列出综合算式。教材中给出的第一种方法是：先算平均每个书架放多少本书，列式为224÷2=112（本），再算每一层书架有多少本书，112÷4=28（本）。第二种方法是：先算2个书架一共有多少层，2×4=8（层），再算一层有多少本，224÷8=28（本）。这样，当把分步算式列成综合算式时，就出现了这三种情况：“224÷2÷4”“224÷（2×4）”“224÷4÷2”。前面两种很好理解，第三种，224先除以4，学生是怎么想的呢？根据以前的课堂经验，不少学生是说不出其中的道理的，少数学生会给出这样的想法：把两个书柜“背靠背”粘在一起，看成一个大书柜，大书柜正、反面都有4K7cm+KGr0tWKGTustQQKmWn8ZkZ1G4vYmSOQgy8rP88=层共“4大层”，这样就可以先求出“1大层”有多少本书，列式是224÷4，然后除以2，算出“1小层”有多少本。看来，学生能想到用第三种方法计算，并不是运算顺序搞错了，而是依据了生活中平均分的经验。另外学生在做连乘、连加、连减这样的“同级”计算题时，不按顺序计算，结果都是一样的。因此，学生就会类推出“同级”的连除题也不用分前后运算顺序。但是，学生在此之前接触到的连除算式都是能整除的，而算式“708÷3÷6”无论先除哪一步，第一步能整除，第二步商后面就出现了余数，而学生在二年级正好学过“有余数的除法”，对计算结果出现余数也不会怀疑。

研讨时，面对上面的问题，部分教师仅关注运算的结果，而对每一步运算的意义、学生的思维过程却不愿做理性的分析。2022年版课标关于数的运算，也提出了新的要求。笔者想据此问题，依照2022年版课标要求，来分析整数除法运算与分数之间的关系，寻找三种方法在运算过程上的相通性。

2.关联不同算法本质上的一致性。

2022年版课标指出：要让学生学会用整体的、联系的、发展的眼光看问题，形成科学的思维习惯，发展核心素养。同时在“数与运算”部分，2022年版课标指出：在解决简单实际问题的过程中，理解四则运算的意义。引导学生了解运算的一致性，体会等式的传递性，形成初步的代数思维和推理意识。如何借助该题，帮助学生体会“运算的一致性”，体会等式的传递性和推理意识，是值得我们思考的。

针对上面的连除算式，三种不同运算过程意义上的一致性和相通性，我们可以从以下几方面来寻找。

（1）根据除法与乘法之间的关系来寻找。

（2）利用“数形结合”“以形解数”来寻找。

为了便于学生理解同一算式不同计算结果，其背后的相通性和相同性，我们也可以利用如下“数形结合”的方式来分析。如把一个大长方形看作被除数，以□÷2÷4为例，把上述三种运算方法利用图形进行演示（图略）。从图中可以清楚地看出，三种方法的运算意义是相通的，仅仅是外在表现形式和程序上不同，我们可以说是“殊途同归”。

（3）从具体的生活情境中来寻找。

（4）从有余数除法的特征和商不变性质来寻找。

[教学思考：]

基于2022年版课标倡导的单元整体结构化教学的要求，笔者认为，在教学“有余数除法”时，要适当丰富学生对“余数”概念的认知，要有“瞻前顾后”的整体教学的意识。“顾后”就是要考虑这一课的教学要为后面哪些相关教学内容服务。如，商不变性质、小数商以及除法与分数之间的关系等。教学时，若教师能适度地拓展和完善学生对商以及商和余数之间的关系的认知，就能为后面学习商是小数的除法奠定基础。

如在例题教学之后，教师可以出示这样的问题：10块巧克力平均分给3个男生，13块巧克力平均分给4个女生，每个男生和女生各能分得几块？学生列出算式：10÷3=3（块）……1（块）、13÷4=3（块）……1（块）。然后教师问学生：“分完了吗？如果继续平均分下去会怎样？”学生会说：“把剩下的1块巧克力再平均分，每人还能分得‘一点’巧克力。”教师接着引导学生说出这“一点”和之前分得的3块合起来就是3块多一点，这个“多一点”不能用我们学过的1、2、3……来表示，以后会学习。这时的商与之前我们认识的商不一样，可以称“临时”“暂时”“不完全”的“商”。两个算式的结果不能说是“3”，而是“3……1”。最后提出问题：“两题中余下的1块巧克力都再继续平均分，每个小朋友得到的这‘一点’巧克力，是一样多的吗？为什么？”通过实物演示和思考，发现每人多出来的这“一点”巧克力不一样大的原因是什么，从而体会余数的相对性。

这样，适时地丰富学生对“余数”的认知，使他们感知到余数与除数相互依存、协同互变的关系，有了结构化认知思维。这样，学生在“灵动”地理解“余数”的同时，为后续学习攒足了“后劲”。