多元表征“分数基本性质”

在北师大版教材五年级上册，“分数基本性质”是在理解了分数意义和学习了分数与除法的关系的基础上安排的学习内容，重点引导学生从“面积模型”的角度表征和理解分数基本性质。这引发了我的思考：面积模型是不是唯一的表征方式？能否多元表征分数基本性质，让学生的思维向更深处漫溯？

为了最大限度发挥学生的主体性，引发学生的思考，我预留10分钟的时间以鼓励学生独立思考并完成任务。在思考与交流中，形成了如下五种表征和理解分数基本性质的方式。

一、从“分数意义”理解分数基本性质

从分的数意义理解分数是数学的本质导向，这一点非常好。但由于文字表征略显抽象，部分学生似乎并不是特别清楚。

二、从“商不变的规律”理解分数基本性质

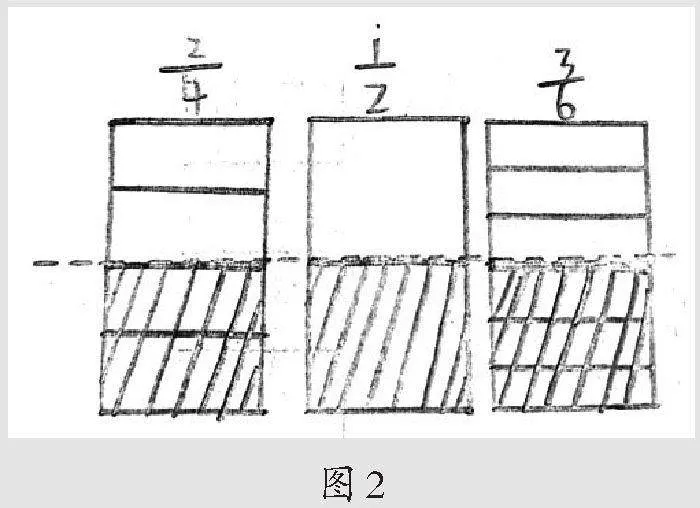
三、从“面积大小”理解分数基本性质

利用“面积模型”表征分数的基本性质是学生容易想到和理解的方法。教学中也有学生画出了水杯图、圆形、正方形等图形来表示1杯水，最终发现三个分数的相等关系。

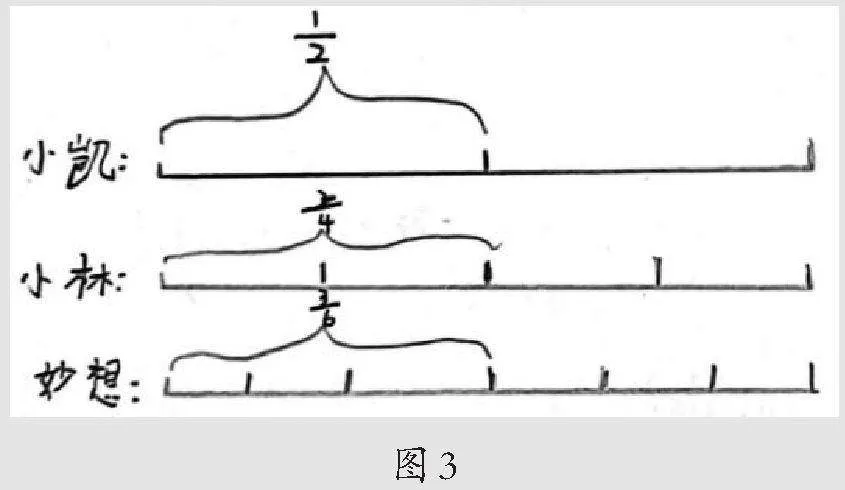
四、从“线段长度”理解分数基本性质

相比于“面积模型”，“线段模型”的产生让我眼前一亮，这是学生抽象思维的一次提升，更是几何直观表征“分数基本性质”的完美升级。

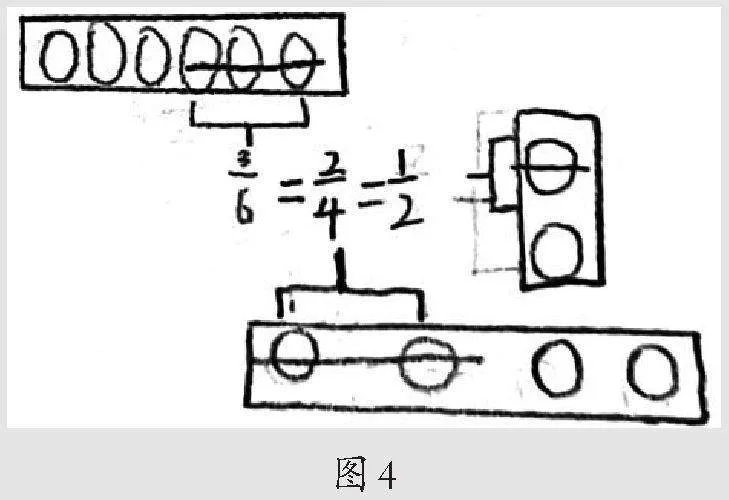
五、从“数量多少”理解分数基本性质

相较于“面积模型”中的同一个长方形、“线段模型”中同样长度的线段而言，图4中的做法以“多个○”表示一个整体，这样的表征方式显得抽象一些，但对于五年级学生来讲，分数的再认识其实就是对“整体”的再认识。须知，“一个整体”不仅是1个图形或1条线段，也可以是多个图形构成的。从这个角度看，这个学生的思维已经上升到了相对较高的境界。

通过如上深入的思考和交流，学生对三个分数之间相等关系的理解就更加清晰了。基于此，分子和分子、分母和分母之间的关系迎刃而解，很快就推演出了“分数基本性质”，取得了很好的学习效果。这样的课堂既达成了学习目标，又引领学生的思维向纵深处发展，可谓一节有效的数学课。当然，这节课更体现了数学在培养人理性思维方面不可替代的价值。