在结构化的题组中梳理提升

“三位数乘两位数”是人教版教材四年级上册的教学内容。这一单元是“数与代数”领域中的重要学习内容之一。对于不仅有计算还有解决问题的单元，如何上好复习课是很值得研究的。对于这个单元的复习课，我们着重设计了结构化的题组，以便让学生在练后自主梳理、在运用中自主感悟。

一、回顾知识，确定复习顺序

（一）直接揭题，回忆知识。

投影展示教材上本单元知识点，引发学生回顾单元知识，教师板书知识点关键词：竖式、积的变化规律、数量关系（“单价×数量＝总价”“速度×时间＝路程”）。

（二）根据单元知识，自主分块。

提出问题：这么多知识，可以分成几部分呢？

学生通过讨论发现这个单元的内容可以分为两部分：一部分是计算，包括竖式和积的变化规律；另一部分是两个基本的数量关系，也可以说是应用。

（三）自主确定复习顺序。

我们怎么进行复习呢？由学生定先复习计算还是复习应用。如学生选择先复习基本数量关系，那就交换下面专项复习的两个环节，先复习第二块内容——基本数量关系。

评析：先回放教材上的主要内容，让学生在观察中对单元知识点进行回顾，接着引发学生对单元知识点分成计算和基本的数量关系两个部分，借此引发学生自主地选择复习顺序。这样的灵活调控会使学生感受自己是学习的主人，从而为以下复习做好积极的心理准备，也使复习过程显得更加自然、流畅。

二、分块复习，经历练中梳理

（一）复习计算。

1.列竖式计算。

198×45= 198×90=

960×25= 480×50=

2.反馈评讲，复习计算方法及注意点。

师：看看这位同学做的，都对吗？（投影展示学生正确的计算过程，图略）第一个算式你是怎么计算的？

生：先用第二个因数的个位“5”去乘第一个因数，再用第二个因数的十位“4”去乘第一个因数，最后把它们的积加起来。

师：做这样的乘法时要注意什么？

生：要注意对位、进位。

师：后面的三个竖式有什么共同的地方？

生：因数的末尾有“0”。

师：因数末尾有“0”又该怎么计算？

生：因数末尾的“0”先不看，算完了在积的末尾添上相同数量的“0”。

师：这样计算，它们分别可以转化成怎样的乘法？

生：三位数乘一位数，两位数乘两位数，两位数乘一位数。

师：再来看第三个竖式“960×25=24000”，最后一个“0”是从哪里来的？为什么可以这样算？

生1：是“960”末尾的“0”不看，最后添回去的。

生2：960可以看成96个十，96个十乘25等于2400个十。

师：那我们来看看这位同学做的，你有什么想说的。（投影展示学生错误的计算，如图1）

生1：“960×25”错在最后忘记添“0”了。

生2：“198×45”错在十位上的“4”乘“198”时进位错了，应该是792个十。

师：他是从竖式中发现了错误，你还可以用其他方法检验吗？

生：把198估成200，200×45=9000，估大了都没有这么大，所以错了。

师：用竖式计算的时候有什么要提醒大家的？

生：要注意进位、对位，因数末尾有“0”的计算最后不要忘记把“0”添回去。

3.沟通三位数乘两位数与两位数乘两位数及多位数乘法的联系。

继续出示如下的三个竖式，（如图2）说一说比较后有什么发现。

比较三位数乘两位数和两位数乘两位数，发现都是先用第二个因数的个位去乘。用个位上的数去乘，积的末尾与个位对齐，用百位上的数去乘，积的末尾跟百位对齐。这时教师继续追问：如果是三位数乘三位数、四位数乘四位数呢？学生总结得出用哪一位上的数去乘，积的末尾就跟那一位对齐。接着追问：为什么这样对位呢？学生回答后师生共同总结出：乘法竖式就是记录几个一、几个十、几个百、几个千……的过程。

评析：三位数乘两位数是整数乘法的最后阶段，复习时需要沟通三位数乘两位数与两位数乘两位数及多位数乘多位数的联系，使学生感受到竖式其实就是记录几个一、几个十、几个百、几个千……的过程，它们只是计数单位叠加的一种形式。学生通过复习感受数的意义与计算原理的一致性。

4.复习积的变化规律。

（1）呈现刚才的四个算式及结果。

198×45=8910 960×25=24000

198×90=17820 480×50=24000

师：仔细观察上面四个算式的因数和积，你有什么发现？

生：第一个算式与第二个算式比较，第一个因数不变，第二个因数乘2，积也乘2；第三个算式和第四个算式比较，第一个因数除以2，第二个因数乘2，积不变。（课件呈现图3）

师：这就是我们学习的积的变化规律，请同学们回忆一下，什么是积的变化规律？

（2）根据第四个算式480×50=24000，应用积的变化规律快速地写出下面几个算式的结果。

120×50=（ ） （ ）×50=48000

160×150=（ ） 480×（ ）=12000

评析：本环节设计了以上四个典型的算式，这为复习积的变化规律埋下伏笔，学生通过计算和观察发现积的变化规律，边算边理，环环相扣，学生在不知不觉中就进入下一个环节。

（3）出示学习材料：比较下面四个算式积的大小。

①242×38= ②240×38=

③240×40= ④238×42=

教师呈现以上四个算式，请学生比较积的大小，学生通过观察比较，只会看出前三个算式中第二个最小，其他的不会比较。教师引导学生通过列竖式计算来比较（如有计算错误的，再次提醒学生计算时要注意的地方）。学生通过列竖式计算发现按积从大到小排列是④③①②。

师：（拿掉第二个算式）观察这三个算式的因数，你有什么发现？

生1：两个因数的和都是280。

生2：两个因数的差不一样。

生3：两个因数越接近，积越大。

师：这让你想到了什么知识？

生：三年级学习长方形周长和面积的时候，同样的周长，长和宽越接近，面积越大。

评析：教师带着学生一起回忆三年级学习的知识：当长方形的周长一定时，长和宽越接近，面积越大；当长和宽相等也就是变成正方形时，面积最大。学生通过这个方法快速得到了三个算式积的大小顺序，与他们计算的结果是一致的。

（二）复习基本数量关系。

1.根据线段图编题。

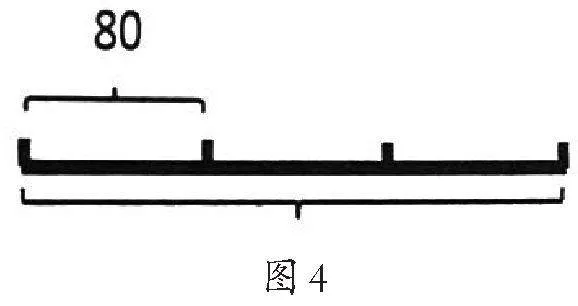
出示要求：猜一猜，这幅线段图（如图4）解决的是什么问题？根据线段图编出两道不同的应用题。

2.反馈各种情况，复习基本数量关系。

（1）投影呈现学生作品。（如图5）

（2）判断正误并说说根据什么数量关系。

板书：单价×数量=总价，速度×时间=路程，每份数×份数=总数。

3.沟通数量之间的关系。

师：这些问题都可以用80×3=240解决，但是表示的意义不一样，它们之间有什么联系呢？

生：单价、速度相当于我们以前学习的每份数，在线段图里都是1段；数量、时间相当于份数，在线段图里表示有3段；总价、路程相当于总数，在线段图里就是总共的长度。

师：如果把“？”放在每份数里或者份数里，你能把这位同学的两道题改一改吗？它们分别用到了哪些数量关系？

引导得出：总价÷数量=单价、总价÷单价=数量、路程÷时间=速度、路程÷速度=时间。继续引导学生寻找以上这些数量之间的关系，并作如下小结：不管是单价、数量、总价，还是速度、时间、路程，它们都似以前学习的每份数、份数、总数之间的关系，表示的都是几个几。

评析：学习计算主要是为了解决相关的实际问题。引导学生把学过的计算应用于相关的实际问题，这样不仅有助于他们感受学习计算的价值，而且有助于他们培养分析和解决问题的能力。结合四年级学生的认识水平，本环节特意选取线段图作为发现数量关系本质的重要工具，从线段图出发自由编题，引出两个数量关系的复习，借助线段图联系旧知，发现这几个数量关系的本质是每份数、份数、总数之间的关系，将数量关系进行结构化的联系，使学生对关系的理解直达根部。

三、联系实际，达到用中提升

（一）在练习中自主感悟。

出示如下两道应用题，学生独立完成。

1.疫情期间，买4个测温器需要584元，白水洋小学要买24个这样的测温器需要多少元？

2.王华骑自行车从家到图书馆，速度是208米/分，24分钟到达。回来时乘小轿车，用了6分钟，小轿车每分钟行驶多少米？

（二）在评价中沟通提升。（如图6）

生：第1题的解法①是用基本的数量关系来解决，先用总价÷数量=单价，再用单价×数量=总价。

第1题的解法②，学生发现如下：

生：用倍比关系，因为买的数量24是4的6倍，因此需要的钱数也是584的6倍。

生：买的测温器价格不变，一个因数乘6，积也乘6，所以只要用584乘6就行了。

生：用积的变化规律来说明，第1题是一个因数（单价）不变，另一个因数（数量）乘6，积（总价）也乘6。

对第2题的两种解法做类似的分析，略。

师：做了这两道题，你有什么收获？

生：解决问题时，我们可以应用基本的数量关系、倍比关系，还可以用积的变化规律来思考。

评析：思维的发散也是数学学习的重要目标之一。本环节结合复习内容精心设计了一题多解的练习题，把今天复习的知识都运用进去了，如列竖式计算、积的变化规律、基本的数量关系等。这使学生在练中再次巩固所学知识，体会问题解决策略的多样性，并学会根据实际情况，灵活地选择解题策略。