发挥作业多维价值撬动课堂教与学方式变革

【课前思考】

“长方体和正方体的表面积”是在学生学习了长方形和正方形的面积和长方体、正方体的认识的基础上教学的。在学习此内容的过程中，教师和学生却常常与错题打交道，不少错题还具有顽固性、隐蔽性、普遍性、反复性，成为学生学习路上的拦路虎。通过课前调研及教师访谈，发现学生的易错点如下。

1.有效信息提取能力不足，由于思维定式而套公式（如图1）。

2.缺乏对生活中数学现象“解读”的能力，找不准要算的面（如图2、图3）。

3.厘不清“面”和“体”的关系，实际应用中经常把面上的长与宽与面的位置关系弄混淆（如图4）。

该如何攻破学生思维的“关键痛处”，揭开本课教学的本质内涵，打通知识的联系，生成多维度的思维模型，培育学生的数学素养呢？结合广东省基础教育学科教研基地项目（江门）开展的小学数学“情智型”作业研究，我们团队进行了探索和实践。

本课以迁移理论为依据，从剖析错题入手，打破传统教学模式，将优化作业设计与课堂教学有机整合，设计符合学生的最近发展区、开发学生高阶思维的“情智型”作业，并以“课前启航”作业→“课中导航”作业→“课后续航”作业为主线贯穿全课教学，努力撬动课堂教与学方式的变革，助力教学提质增效。

全课设计了三个层次的“情智型”作业，帮助学生经历“操作感知—抽象概念—构建意义—应用深化”的全过程，帮助学生将点状知识结构化，让碎片化的学习过程变得结构有序。这种教学模式注重让学生通过自主学习主动获取学习经验、构建新的知识脉络、形成新的策略方法，从而指向高阶思维的发展。

【教学过程】

一、情智型“课前启航”作业，点燃学习内驱力

1.汇报“课前启航”作业，找准新知链接点。

课前，通过启航作业，学生独立探究了核心问题：“制作小金山箱，至少需要多大面积的材料？”上课伊始，再次播放金山伯奋发图强、衣锦还乡的视频，介绍金山伯、金山箱的历史由来。感受历史文化的同时引出制作小金山箱纪念品，计算其用料的面积。

师：课前，大家通过启航作业，扫码了解了金山伯、金山箱的故事。现在，跟随镜头再来回顾一下吧！

播放金山伯、金山箱的故事视频，如图5。

师：如此看来，金山箱有重要的纪念意义。老师也布置了两人合作用小棒、卡纸制作一个长方体的金山箱，并计算至少需要多少平方厘米的卡纸，我们一起看看大家是怎么制作的。

出示学生制作过程的图片，图略。

【教学思考】借助“课前启航”作业，抛出让学生设计小金山箱纪念品的大情境和大问题，不仅引发学生求表面积的需求，又孕育家乡情怀，有效落实核心素养。

2.交流金山箱用料，突破新知落脚点。

师：想一想，大家手上的金山箱有几个面？制作它至少需要多少平方厘米的卡纸呢？把你们的想法在小组内交流和分享。

小组分享交流“课前启航”的作业成果，作业单如图6。

师：哪个小组上来说说你们的想法？老师为你们准备好每个面都可以取下来的长方体，交流时可以边说边摆。

组1：我们的计算方法是“长×宽×2+长×高×2+宽×高×2”。

师：你们的方法是经过调整得到的，能和大家分享一下你们思考的过程吗？

组1：原来我们是1个面1个面相加的，经过小组讨论后进行了优化。

师：想一想，他们的计算方法是把长方体的6个面分成了几组？

生：分成了三组。

师：请大家利用平板电脑拖动对应的面，再详细讲讲这种方法。

学生利用平板电脑动手操作并交流，明白了为何要分成三组。

师：除了这种方法，还有其他想法吗？

组2：我们计算的方法是“（长×宽+长×高+宽×高）×2”。

师：能看懂他们的方法吗？谁来说一说？

生：他们是把一个长方体分成了两组，一组是它的上面、前面和左面，另一组是它的下面、后面和右面，所以可以先算3个面的面积之和，再乘2。

师：我们再来看看这两种方法，它们共同的地方是什么呢？

生：都是在求这个长方体6个面的面积之和。

师：是的，无论是逐一算，还是分组算，都是求这6个面的面积之和。数学上长方体6个面的面积之和称为长方体的表面积。

师：长方体有表面积，正方体也有吗？什么是正方体的表面积？

生：正方体6个面的面积之和就是正方体的表面积。

师：正方体的表面积又该怎么计算呢？

生：正方体的表面积等于“棱长×棱长×6”。

师：如果这个正方体的棱长是2分米，它的表面积是多少？

生：2×2×6=24（平方分米）。

师：请大家仔细观察，长方体和正方体表面积的计算方法有什么联系？

生1：都是求6个面的面积之和。

生2：计算长方体表面积的计算方法同样适用于正方体的表面积。

生3：当长方体的长、宽、高都相等时，就变成了正方体。

【教学思考】这一过程体现了情智型“课前启航”作业自然生成与知识建构的过程。在汇报交流时，鼓励学生探索计算方法，在多种方法中体验解决问题策略的多样性，理解长方体和正方体表面的大小就是它6个面的面积和。同时，注重资源整合，充分发挥白板、多媒体等信息技术的优势，借助几何直观、数形结合，突破本节课的重点和难点。

二、情智型“课中导航”作业，撬动思维进阶力

1.情境开放，融入生活，提升知识关联。

教师出示情智型“课中导航”作业（如图7），在解读问题中提出任务。

师：想一想，这次装修场馆包括哪些项目？

生：粉刷体验馆内部。

生：还要购买展示柜。

师：怎么用好这笔钱呢？请小组合作完成任务。需要提醒大家的是，在探究的过程中，大家有任何疑问，都可以借助平板电脑中的全景图进行观察。

学生分组研讨，教师巡视并指导。

2.深度探究，多维体验，促进素养生成。

师：哪一组来谈一谈你们的想法？

组1：按照问题的设定，我们计划粉刷5个面的墙壁，购买1个展示柜。

师：对他们的计划，有什么问题吗？

生：长方体不是有6个面吗？怎么就粉刷5个面呢？

生：地面不用粉刷。

师：请给大家展示一下你们组的计算方法。

组1：体验馆内部粉刷需要的费用为：[（10×6×2+6×8×2+10×8）-16]×100=28000（元）；购买玻璃做成的展示柜的费用为：（0.8×1+1×2+0.8×2）×2×200=1760（元），一共的费用为：28000+1760=29760（元）。

师：大家还有别的想法吗？

组2：我们小组是粉刷了4个面，买了5个展示柜。

生：你们怎么粉刷了4个面呢？

组2：地面和天花板都可以不粉刷。

师：来，展示一下你们的算法。

组2：体验馆内部粉刷需要的费用为：[（10×6×2+6×8×2）-16]×100=20000（元）；购买玻璃做成的展示柜的费用为：（0.8×1+1×2+0.8×2）×2×200×5=8800（元），一共的费用为：20000+8800=28800（元）。

师：在粉刷墙壁时，大家根据实际需要，有时候可以粉刷5个面，有时候也可以粉刷4个面。在这个学习的过程中，你有什么收获？

生1：我学会了计算长方体和正方体表面积的计算方法。

生2：我懂得了长方体和正方体表面积都是6个面的面积之和。

生3：我学会了在粉刷墙壁时，可以粉刷4个面，也可以粉刷5个面，要根据实际情况灵活运用。

师：在我们的生活中，有不少这样的例子，如制造烟囱、金鱼缸等（呈现相关图示，图略），解决至少需要多大面积的材料时，其实就是求烟囱的4个面的面积和、金鱼缸的5个面的面积和等。

师：接下来，让我们启动“课后续航”作业，在原来设计方案的基础上，继续为体验馆添加不同类型的玻璃展示柜和配备其他物品，并做好第二次装修资金的预算。

【教学思考】“课中导航”作业从能力素养导向出发，培养学生的高阶思维。通过创设一个生活中的大情境，鼓励学生设计装修方案并计算装修成本，深度理解求表面积不一定要“面面俱到”，而是要根据实际情况来判断，这使学生在认知上有一个质的飞跃，真正实现用数学解决生活问题。

三、情智型“课后续航”作业，提升学生学习力

1.开放式的探究题——提升思维。

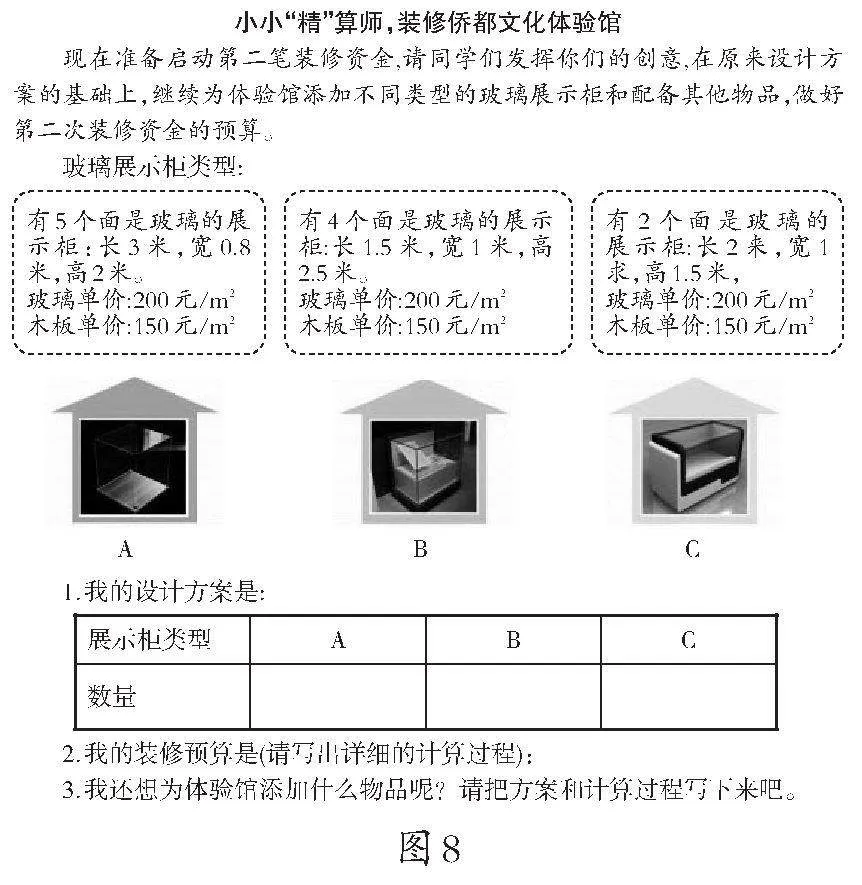
在探究第二笔装修资金预算的过程中，学生不仅要考虑不同类型的玻璃展示柜，还要考虑怎样装饰以及把体验馆设计得更好等。让学生会根据实际情况，灵活运用所学知识解决生活中的实际问题，培养学生的推理意识、模型意识。同时，本题（如图8）以开放式的探究形式呈现，让数学作业“有趣”“有情”“有思”“有用”。

2.“错”中生慧学习吧（纠错微课）——巩固基础。

为了满足不同层次学生的不同发展需求，引导学生自主学习，专攻薄弱环节，打通“痛点”，达到“知其然也知其所以然”的高境界，请学生扫码观看“错”中生慧学习吧（纠错微课）——《计算表面积并不一定要“面面俱到”》（如图9），从三个层次展开：启思维，解疑惑→巧运用，速掌握→素养成，玩学乐，提升学生的学习力。