“四边形的再认识”

本节课的教学目标定位是：通过分类、比较和归纳等方式，从多维度感悟四边形的特征，明确特征要素是边的位置关系；理解并掌握平行四边形和梯形的基本特征，梳理四边形之间的关系。

环节一：明确平行四边形和梯形的基本要素是边的位置关系

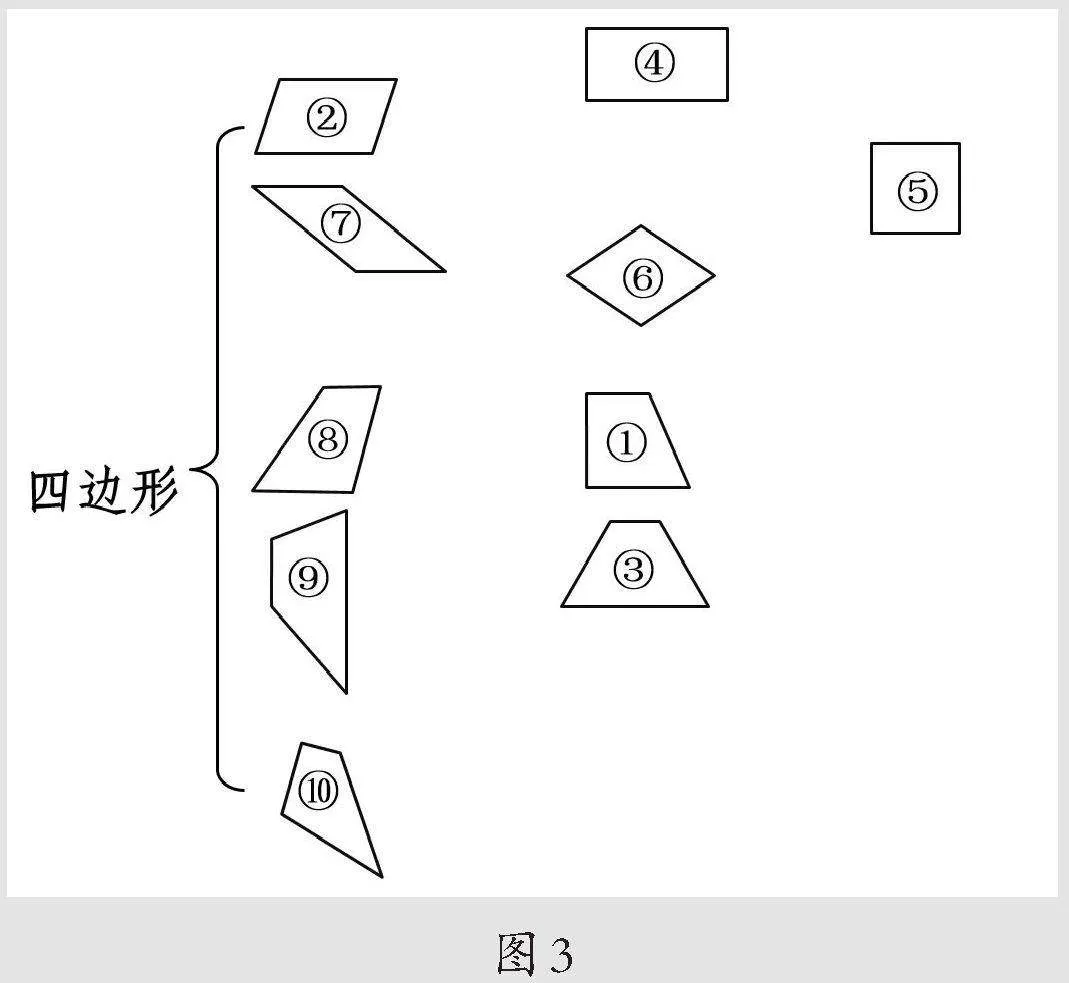
1.布置任务：这些四边形（如图1）中，哪些是平行四边形和梯形？

2.学生自主尝试，认为②⑥⑦是平行四边形，①③⑧是梯形，其他的存在争议。

3.交流反馈。

师：能说说你心目中的平行四边形和梯形是什么样子吗？

生：平行四边形是平的，梯形是像梯子一样斜斜的。（提取要素：角度）

生：平行四边形是对边平行的，梯形有两条边会相交。（提取要素：平行）

生：平行四边形的上边和下边长度一样，左边和右边长度一样，梯形的不一样。（提取要素：长度）

【设计意图】这组材料有效地激活了学生已有的知识和经验，据此引发学生思辨。学生对平行四边形和梯形已经积累了一定的表象，但对其特征的认识尚处于零散、非理性的直觉判断阶段。学生能从这些图形中找到常规的平行四边形和梯形，但是对长方形、正方形和位置倾斜的非常规图形存在疑虑。

4.确定研究平行四边形和梯形的特征要素是平行。

师：你们说到了角度、长度和平行这几个要素，那么，平行四边形和梯形到底是根据什么要素判断的呢？

生：我觉得是平行，因为平行四边形和梯形中各种角都有。

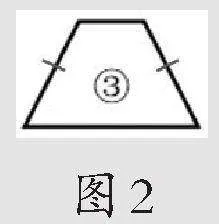
生：我也觉得是平行，因为梯形对边的长度有可能相等，也有可能不相等，图形③中有一组对边就是相等的。（学生边说边指出相等的边，如图2所示）

生：平行四边形的名字中带着“平行”呢，我们刚学过，应该是平行。

师小结：是的，平行是判断平行四边形或梯形的特征要素。

出示任务：找一找这些四边形中的平行线，再尝试分类。

师：现在有需要调整的吗？还有哪些也是平行四边形或梯形呢？

生：图形④⑤虽然有自己的名字，但它们也是平行四边形，因为它们都是两组对边分别平行的图形。图形⑨是梯形，因为它只有左、右这组对边平行。

学生调整分类结果，认为②④⑤⑥⑦是平行四边形，①③⑧⑨是梯形，⑩是一般四边形。

师：你们认为图形⑩既不是平行四边形也不是梯形，为什么？

生：图形⑩两组对边都不平行。

师小结：图形⑩既不是平行四边形也不是梯形，像这样的图形叫一般四边形。

【设计意图】这个环节中，学生通过图形分类的操作活动，明确判断平行四边形和梯形的特征要素是平行，并依据图形中平行线的组数进行分类探讨，排除长度、角度等次要要素，建立概念。

环节二：以长度和角度为要素，梳理四边形之间的关系

师：刚才我们根据对边是否平行把四边形分成了三类——平行四边形、梯形和一般四边形，那么，长度和角度又有什么作用呢？

1.布置任务：给你们分好类的四边形排排队，考虑长度和角度因素，把最特殊的放在后面。

2.学生自主尝试，教师整体呈现学生作品，如图3所示。

3.交流反馈。

师：你们都赞同吗？请说明理由。

生：我觉得长方形、菱形、正方形都有平行四边形的特点，而且特殊，直角梯形和等腰梯形是特殊的梯形。

师追问：它们特殊在哪里？

生：菱形的边长度都相等，长方形的邻边垂直，正方形的四条边互相垂直且相等。

生：等腰梯形两条腰的长度相等，直角梯形有两条邻边垂直。

师追问：平行四边形中，哪个图形最特殊？

生：正方形。

师追问：为什么这么认为？

生：正方形不仅满足对边平行和相等，而且满足邻边垂直和相等，所以正方形不仅是特殊的平行四边形，还是特殊的长方形和特殊的菱形。

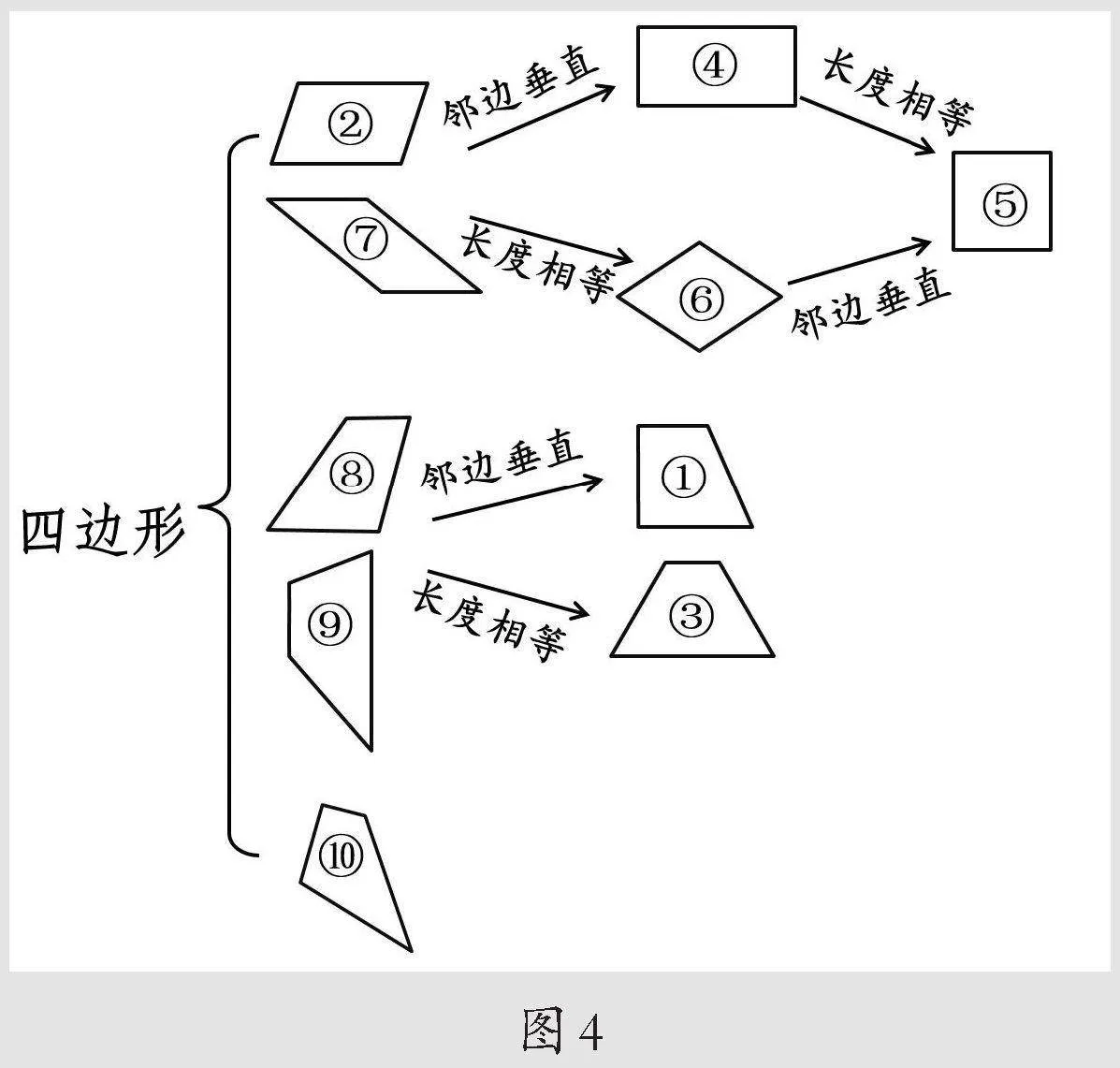
师生共同将四边形分类，如图4所示。

4.小结。

师：刚才我们根据对边是否平行将四边形分成了平行四边形、梯形和一般四边形，又根据角度和长度找到了特殊的平行四边形和特殊的梯形。平行是两条对边的位置关系，角度是两条邻边的位置关系，长度是边的长短，它们都在研究边。

【设计意图】本环节中，学生从一般到特殊给四边形排队，意在从边的长度和角度进一步探讨图形的特殊性，初步体验平行是图形分类的特征要素，长度和角度是一般和特殊的区分要素，并进一步提炼概括图形的特征要素是边。

环节三：直观表征，进一步明晰概念的内涵和外延

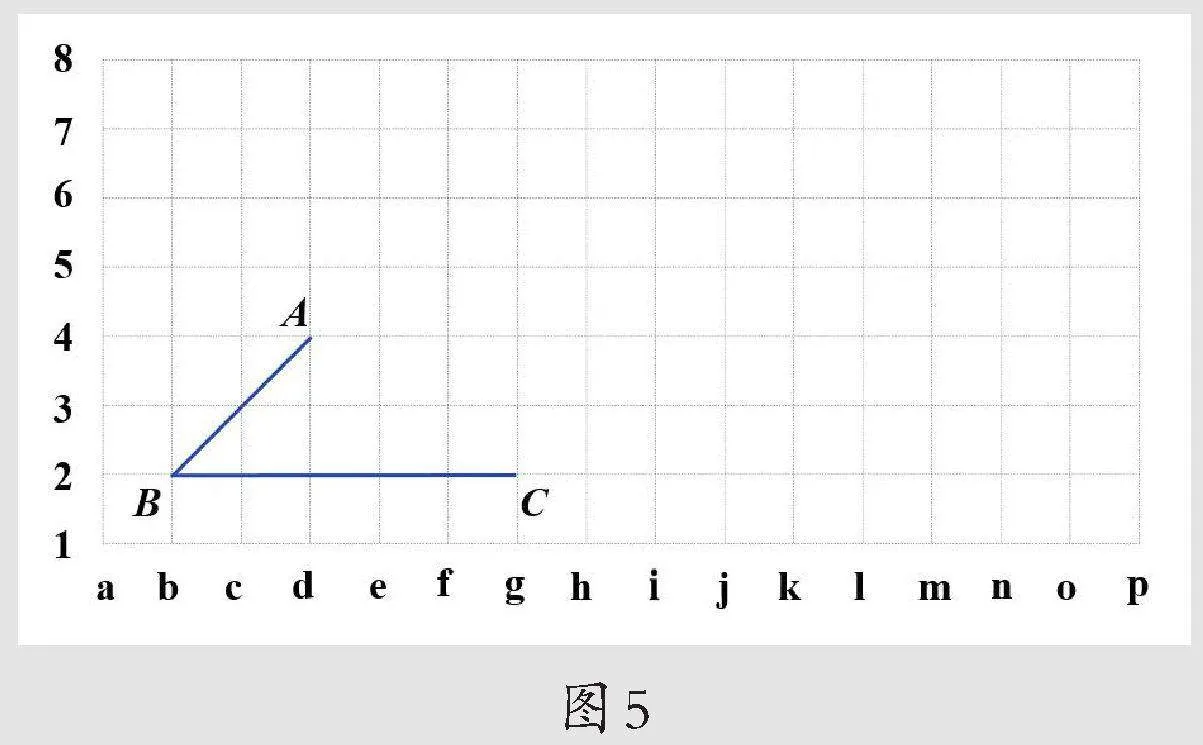
1.布置任务：如图5，找点D，与点A、B、C围成平行四边形；找点E，与点A、B、C围成梯形。

2.学生自主尝试。

3.教师整体呈现学生作业，学生交流和反馈。

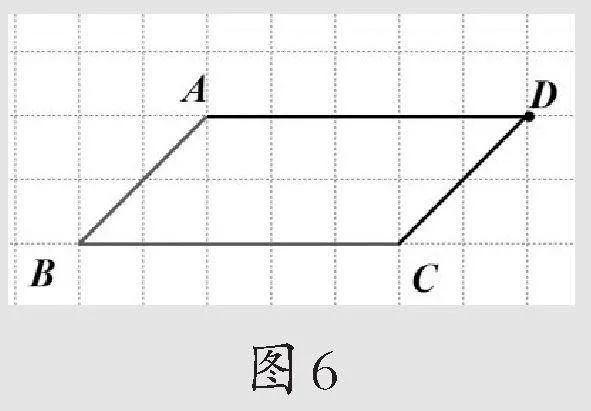
师：点D只能在这里（如图6所示）吗？请说说理由。

生：点D只有在这里才符合两组对边分别平行的要求。

生：平行四边形的两组对边长度相等，下边是5格，上边也是5格。

师小结：通过两组平行线的交点我们找到了点D，点D是唯一的。

师：你们找到多少个满足条件的点E？

学生报点的位置，课件同步呈现，如图7所示。

师：为什么这两条射线上的点都可以，但是这个点（指点D）除外？

生：梯形只能有一组对边平行，这个点会导致出现两组对边平行，围成的是平行四边形。

师：如果随意找一个点F，与点A、B、C围成一般四边形，可以在哪里找？

生：点F要在这个面上，但是不能在射线BA、BC、AD、CD上。

【设计意图】利用概念的内涵，寻找四边形的第四个顶点，学生发现只有一个点满足围成平行四边形，但是有无数个点满足围成梯形，从而对梯形有了更深刻的认识。