基于欧拉双流体模型的微小井眼环空岩屑运移数值模拟研究

张鑫鑫 ，毛纯芝 ，信伟卫，张绍和 ，吴冬宇 ，贺勇

(1. 中南大学 有色金属成矿预测与地质环境监测教育部重点实验室，湖南 长沙，410083；2. 中南大学 地球科学与信息物理学院，湖南 长沙，410083；3. 江西有色地质矿产勘查开发院，江西 南昌，330001)

近年来，油气勘探开发工作的重心逐渐向老油田、边际油气藏和非常规油气藏等对钻采技术要求更高的油气藏能源转移[1-3]，同时，绿色勘探理念的推广也给钻探新工艺新方法提出了新要求。微小井眼钻井技术具有费用低、污染低、对储层伤害小的优点[4]，国内外研究人员相继开展了对该技术的研究[5]。相较于常规井眼和小井眼，微小井眼最大直径仅88.9 mm[6]，且需结合连续油管滑动推进进行钻进工作[7]。微小井眼钻井技术具有井眼直径小、环空间隙小且连续油管在井中无法旋转的特点，导致钻井在水平井段及大斜度井段钻进困难。一方面，微小井眼在钻进过程中钻压施加困难，钻杆易发生屈曲现象，导致钻速低、摩阻高，容易发生如卡钻、埋钻等井下事故[8]；另一方面，水平井段的岩屑颗粒受到重力作用，容易在环空底部形成岩屑床，而钻柱无法旋转，增大了岩屑的携带难度[8-9]。为保持良好的井眼清洁效果，有必要针对微小井眼钻井水平井段及大斜度井段岩屑运移规律开展研究。目前，岩屑运移规律研究主要有经验模型、理论模型和计算流体动力学(CFD)模型[10-12]。近年来，诸多学者对岩屑运移进行了研究，如：胡金帅等[13]基于CFD 和离散元耦合(DEM)模型模拟和分析了不同工况下岩屑颗粒在固液两相流状态中的流动规律；朱娜等[14]通过建立2层动态岩屑床运移模型模拟了大位移井复杂工况下的岩屑运移规律；孙晓峰等[15]利用漂移流动模型建立了环空固液两相流动模型，进而对岩屑床高度进行了瞬态模拟，并通过CFD 数值模拟探究了钻杆轴向运动对水平井段岩屑运移的影响机制[16]；宋先知等[17]通过数值模拟建立了混合相漂移模型，研究了连续油管岩屑运移规律；汪皖等[18]提出了连续油管旋转管柱钻进系统，运用数值模拟方法研究了钻杆旋转对岩屑运移的影响。尽管人们对常规井眼及连续油管钻进过程中的岩屑运移规律进行了总结与归纳，但针对微小井眼环空岩屑运移机制及各参数影响规律的研究仍较少。为此，本文作者在分析岩屑运移机理及运移模式的基础上，通过CFD 数值模拟建立微小井眼环空流域内岩屑固液两相流模型，研究不同岩屑特征、工作参数、井筒环境和钻杆振荡对岩屑运移规律和运移模式的影响机制，以便为微小井眼技术水平井段及斜井段岩屑颗粒运移研究提供理论参考。

1 岩屑运移模式

在实际钻进工作中，岩屑颗粒受力极其复杂，为方便建立模型，对岩屑受力情况进行适当简化。环空内的岩屑颗粒在垂直方向上主要受到重力作用，在运移方向上主要受到流体的拖曳力和压力梯度力作用，在沉降方向上主要受力为岩屑床的支撑力、举升力。在各力的综合作用下，岩屑颗粒在环空井筒内主要有悬浮层、移动床、固定床共3种运移形状态，而根据工作参数的不同，可能出现如图1所示的5种运移模式[19]。

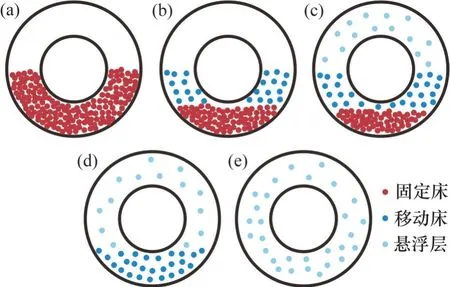
图1 岩屑运移模式示意图Fig. 1 Schematic diagrams of cuttings transport pattern

2 数值模拟研究

2.1 模型方程的建立

2.1.1 控制方程

本研究所有模拟案例都采用欧拉-欧拉双流体模型进行模拟计算。基于颗粒动力学理论[20]将液相与固相均视为连续相，液相和固相的连续性方程可表示为

其中：αq为q 相的体积分数；ρq为q 相密度，kg/m3；vq为q相速度，m/s。

液相和固相的动量平衡方程可以表示为

其中：g为重力加速度，m/s2；vp为第二相p 的速度，m/s；Kpq为相间动量交换系数；Fq为q相所受到的外部作用力，N；Flift，q为q 相升力，N；Fwl，q为q 相壁面滑移力，N；Fvm，q为q 相虚拟质量力，N；Ftd，q为q相湍流耗散力，N；τq为q相应力应变张量。

2.1.2 颗粒温度模型

由于颗粒温度与颗粒随机运动的动能成比例关系，因此，基于动能理论可得到如下固相输运方程[20]：

式中：αs为固相体积分数；ρs为固相密度，kg/m3；vs为固相速度，m/s；θs为颗粒温度，℃；ps为固体压力，Pa；I为单位张量；τs为固相的应力应变张量；kθs为扩散系数；γθs为碰撞耗散能量，kg/(m·s-3)；χls为液相与固相间的能量交换量，kg/(m·s-3)。

2.1.3 曳力模型

本研究中，采用GIDASPOW 模型[21]确定固液两相间动量交换系数Ksl，其表达形式如下：

式中：CD为曳力系数；αl为液相体积分数；ρl为液相密度，kg/m3；vl为液相速度，m/s；μl为液相剪切黏度，Pa·s；ds为固相粒径，mm；Res为相对雷诺数。

2.1.4 升力模型

采用SAFFMAN-MEI 模型[22-23]模拟升力Flift，其形式可表示为：

式中：Cl为升力系数；Rep为颗粒雷诺数；Reω为涡度雷诺数；β=0.5(Reω/Rep)。

2.2 CFD模型建立及求解

参考国内外生产案例及相关研究应用的井眼和钻杆直径[24]，确定模拟所用的流体域几何模型整体为一中空的圆柱体，e为偏心度，模型外径为70 mm，内径为38 mm，轴向延伸长度为3 m，属于微小井眼。为保证计算结果精度，本研究采用六面体网格进行流体域网格划分，网格具体参数见表1，几何模型及网格示意图见图2。

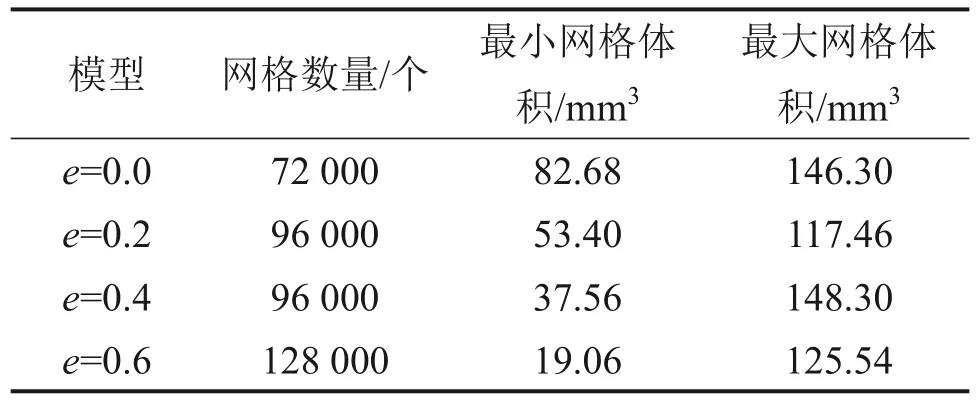
表1 网格参数Table 1 Parameters list of grid

图2 几何模型和网格示意图Fig. 2 Schematic diagram of geometric model and mesh

基于欧拉-欧拉模型研究固液两相流，钻杆振荡模型采取瞬态计算，利用动网格技术模拟钻杆在轴向方向的振动特征，其余操作参数模型均采取稳态计算。选用Standardk-ε湍流模型，固相颗粒假设为球形，密度为2 600 kg/m3；循环介质选择清水，密度为998.2 kg/m3，黏度为1.003×10-3kg/(m·s)。颗粒与液相均按照设定的速度从入口进入流场，出口设置为自由流出边界，液相与壁面间无滑移，固相与壁面间镜面系数设定为0.1，采用一阶迎风格式和SIMPLE压力速度耦合算法进行模型离散和求解。

2.3 模拟方案设计

本研究需探究微小井眼钻井技术中影响岩屑运移的7 个因素，包括环空流体速度、岩屑直径、机械钻速(ROP)、钻杆偏心度、井斜角、钻杆振荡频率及幅度。探究某一因素对岩屑运移规律影响时，其余参数保持不变，每一试验组单独设计4～7组模拟试验，具体模拟参数范围见表2。

3 数值模型验证试验

为验证数值模拟的可靠度，本研究利用一套微小井眼岩屑运移试验装置进行水平井段试验，装置外径为70 mm，内径为38 mm，主要分为动力系统、加砂系统、模拟井筒系统、高速摄像系统、岩屑过滤及收集系统、倾角调节系统、数据采集系统、控制系统共8 个部分，装置示意图如图3所示。

图3 试验装置示意图Fig. 3 Schematic diagram of the experimental device

试验采用水作为循环介质，密度为998.2 kg/m3，黏度为1.003×10-3kg/(m·s)；试验用砂选择直径为2 mm 的氧化锆陶粒(ZrO2)，密度为2 622 kg/m3。试验设置0.6、0.8、1.0 m/s 共3 组环空流速进行研究，加砂速度为0.012 kg/s，井斜角设定为90°，由此得到不同环空流速下岩屑床高度及环空单位长度压降，将得到的试验压降与数值模拟压降进行比较，对比结果如图4所示。由图4可知：数值模拟压降与试验压降较吻合，最大相对误差仅为8.91%，验证了数值模拟计算结果的可靠性与准确性。

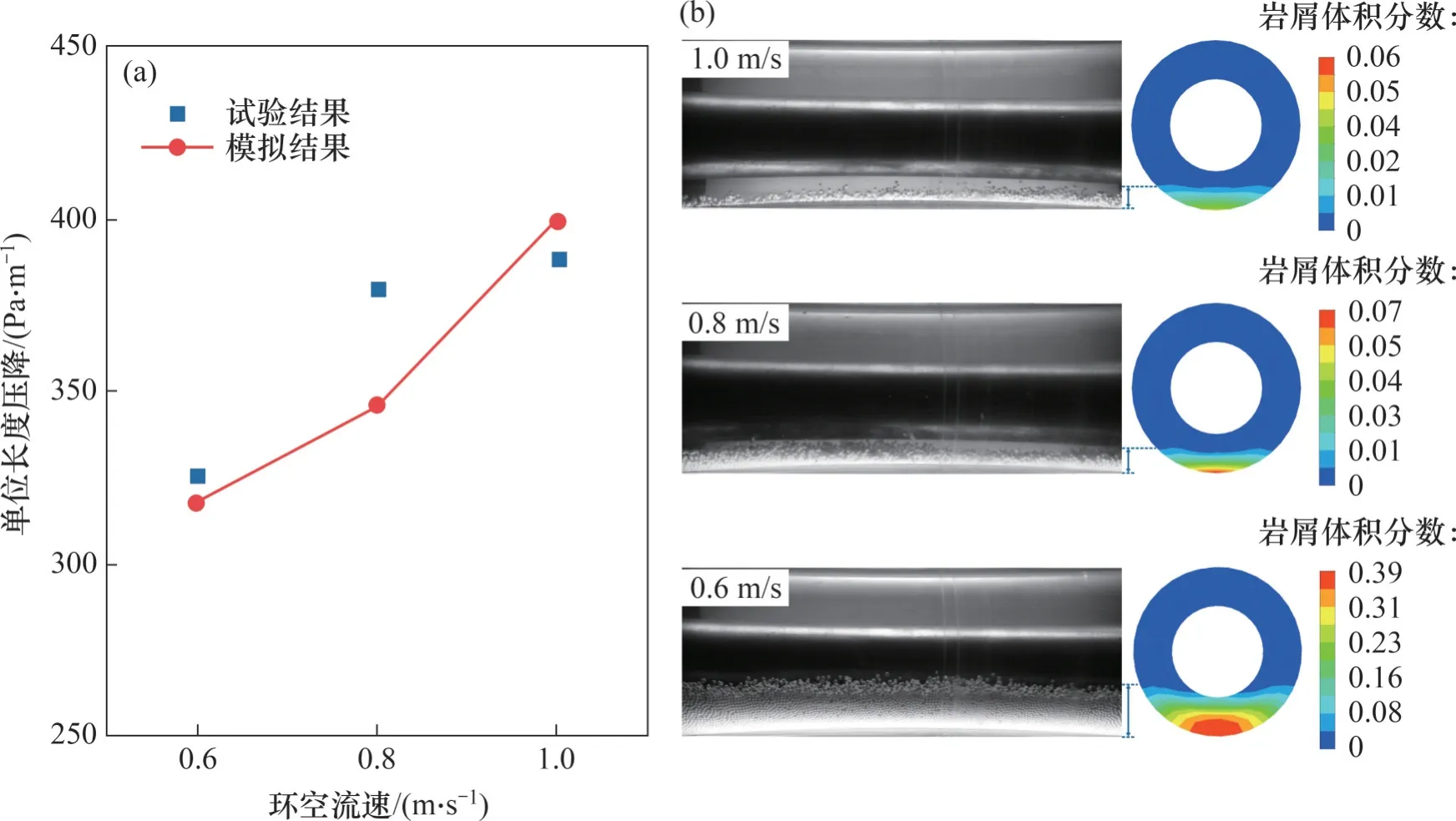
图4 不同环空流速下数值模拟与试验结果比对Fig. 4 Comparison of numerical simulation and experimental results at different velocities of liquid in annular space

4 数值模拟结果分析

4.1 环空流速对岩屑运移的影响

不同环空流速下岩屑体积分数分布如图5 所示。从图5可见：随着环空内液相初始速度逐渐增加，岩屑平均体积分数逐步降低，且环空截面岩屑体积分数呈现相同下降趋势；在其他参数不变时，流速增加可以显著提升钻井液携岩效率，其原因是流体增速可引起流体与颗粒间相互作用力增加，即在运移方向上，流体的拖曳力会随环空流速增大而增大，使得颗粒运移速度增大，井眼净化效果提高。

图5 不同环空流速下岩屑体积分数分布Fig. 5 Distribution of cuttings volume fraction at different velocities of liquid in annular space

4.2 岩屑直径对岩屑运移的影响

不同岩屑直径下岩屑体积分数和岩屑截面速度分布如图6所示。从图6可见：随着颗粒直径从0.5 mm 增大到2.5 mm，岩屑平均体积分数、岩屑入口附近及出口附近的速度均呈现先增大后减小的趋势，而与出口附近岩屑速度相比，入口附近速度分布更均匀；粒径为0.5 m的颗粒主要以悬浮状态运移，速度分布较均匀，运移效率高；当粒径为1.0 mm 时，颗粒较难上升至悬浮层，致使底部移动床堆积，但流道短暂变窄会导致两侧颗粒速度有所上升，此后，由于运输大直径颗粒需要的能量更高，岩屑运移速度会随着粒径增大逐渐下降，同时，粒径越大，单个岩屑所受重力越大，越易沉降至环空底部，因而，当粒径由0.5 mm 增至1.5 mm 时，岩屑体积分数逐渐达到最大值；而在岩屑初始体积分数不变的情况下，粒径增大也会导致进入环空的岩屑数量减少，这在一定程度上可以降低因相邻颗粒和颗粒壁面间碰撞带来的能量损失。从图6(a)可见：当粒径由1.5 mm 增至2.5 mm时，岩屑颗粒数量减少带来的有益效果占据主导地位，岩屑平均体积分数呈下降趋势。

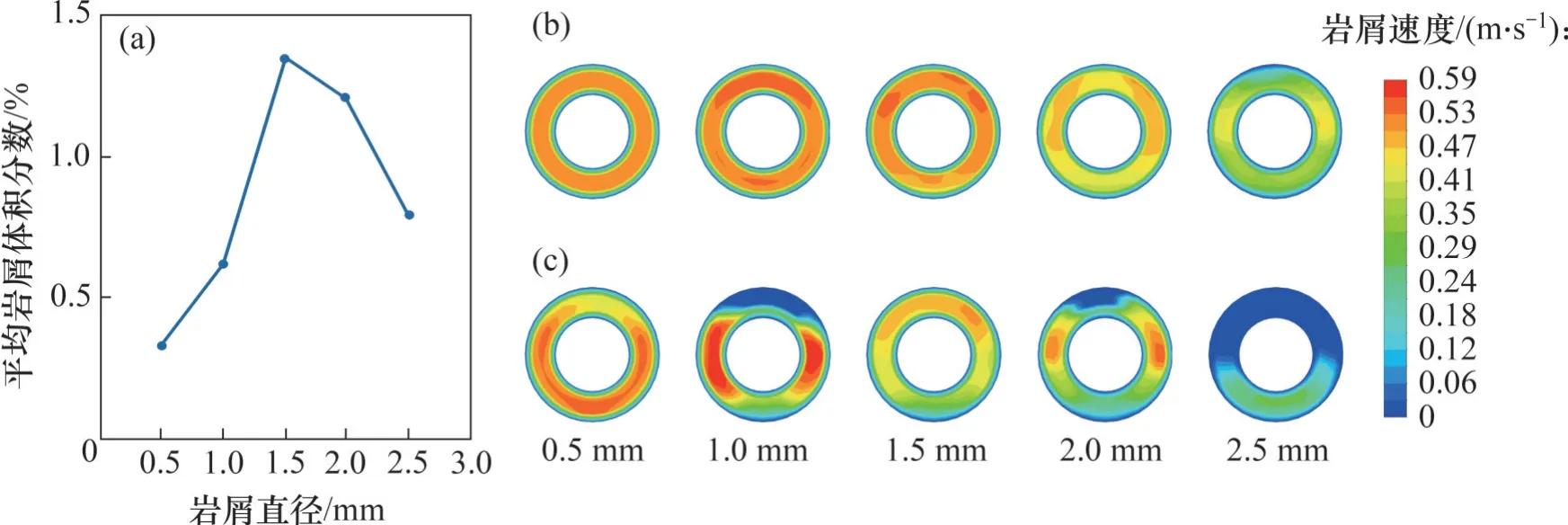
图6 不同岩屑直径下岩屑体积分数和岩屑截面速度分布Fig. 6 Distribution of cuttings volume fraction and cuttings cross-sectional velocity for different cutting diameters

4.3 机械钻速对岩屑运移的影响

机械钻速(ROP)表示单位时间内的钻进尺度。不同机械钻速下单位长度压降和截面岩屑体积分数、岩屑速度分布如图7所示。从图7可见：管内压降、岩屑体积分数、岩屑速度均会随着ROP 的增加逐渐增大；在岩屑初始体积分数不变的情况下，随着钻速增加，岩屑进入环空的初始速度逐渐增大，管道内颗粒运移速度也增大，但在单位时间内进入的岩屑颗粒数量增加，使颗粒间碰撞所损失的能量增加，导致单位长度压降升高，也使得管内沉积的岩屑体积分数逐渐增加。可以认为，适当地提高钻速会提高钻井液携岩效率，但钻速过高会使得岩屑堆积过快，减小岩屑运移速度，不利于岩屑顺利运移出环空。从图7 还可见：当机械钻速增加到10 m/h时，与机械钻速8 m/h相比，管内压降与岩屑体积分数急剧升高的同时，环空底部岩屑床运移速度明显降低，岩屑运移模式从移动床向固定床转变，此时，可以通过提高环空流速来增大井眼净化效率。

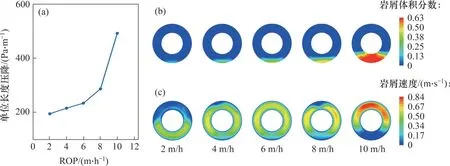
图7 不同机械钻速下压降和截面岩屑体积分数、岩屑速度分布Fig. 7 Distribution of pressure drop,cross-sectional cuttings volume fraction and cuttings velocity at different ROP

4.4 钻杆偏心对岩屑运移的影响

在水平段钻进过程中，由于重力作用的影响，钻杆倾向于靠近下井壁，使得钻杆下部环空间隙变窄，造成钻杆偏心现象。不同偏心度下岩屑体积分数和截面岩屑速度分布如图8所示。从图8可见：与同心钻杆相比，在偏心状态下，岩屑总体积分数显著上升，入口及出口附近的岩屑速度均随偏心度增加而降低，且在偏心工况下，颗粒易在宽间隙处形成高速流动区；当钻杆偏心度为0.2时，在钻杆前半部分，岩屑主要以移动床加悬浮状态运移，而随着运移距离增加，岩屑在钻杆后半部分急剧堆积，岩屑体积分数最高可达到63%，岩屑主要以固定床加移动床模式移动；随着钻杆偏心度增加到0.6，岩屑仅在距入口0～0.4 m 范围内以移动床加悬浮状态运移，这说明岩屑在环空内运移难度随偏心度增加逐渐增大。

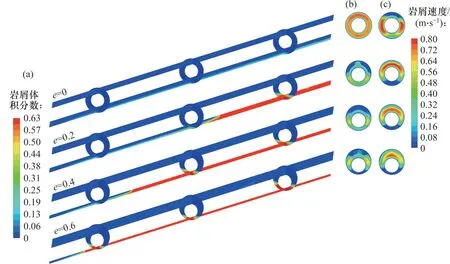
图8 不同偏心度下岩屑体积分数和截面岩屑速度分布Fig. 8 Distribution of cuttings volume fraction and cross-sectional cuttings velocity under different eccentricities

4.5 井斜角对岩屑运移的影响

在实际的水平井钻进工作中，钻进轨迹需经过倾斜井段后再到水平井段，因而，有必要考虑井斜角对岩屑运移的影响。为量化表征岩屑运移效率，特引入岩屑输送比，其定义为环空内岩屑平均速度与钻井液平均流动速度之比。不同井斜角下岩屑体积分数、压降和岩屑输送比分布如图9所示。从图9可见：随着井斜角增加，平均岩屑体积分数总体呈现先增加后减小的趋势，与水平及垂直井段相比，倾斜井段的岩屑体积分数明显更高，且在井斜角为60°时平均岩屑体积分数达到最大值(见图9(a))；而由于水压力影响，压降则随井斜角增大逐渐下降(图9(c))；随着井斜角增加至60°，岩屑运移形式逐渐从悬浮变为滚动，且颗粒倾向于向管道底部沉积，致使环空前半部分出现高体积分数区域(图9(b))。图9(d)显示了岩屑输送比(即环空内岩屑平均速度与液相平均速度之比)随井斜角的变化趋势，可见在高井斜角阶段，随着井斜角增加，岩屑受重力分量带来的运移阻力逐渐降低，岩屑运移效率呈升高趋势。此外，井斜角为30°与井斜角为60°时相比，岩屑输送比略低，但考虑岩屑体积分数，可以认为井斜角为60°时携岩效率最低。

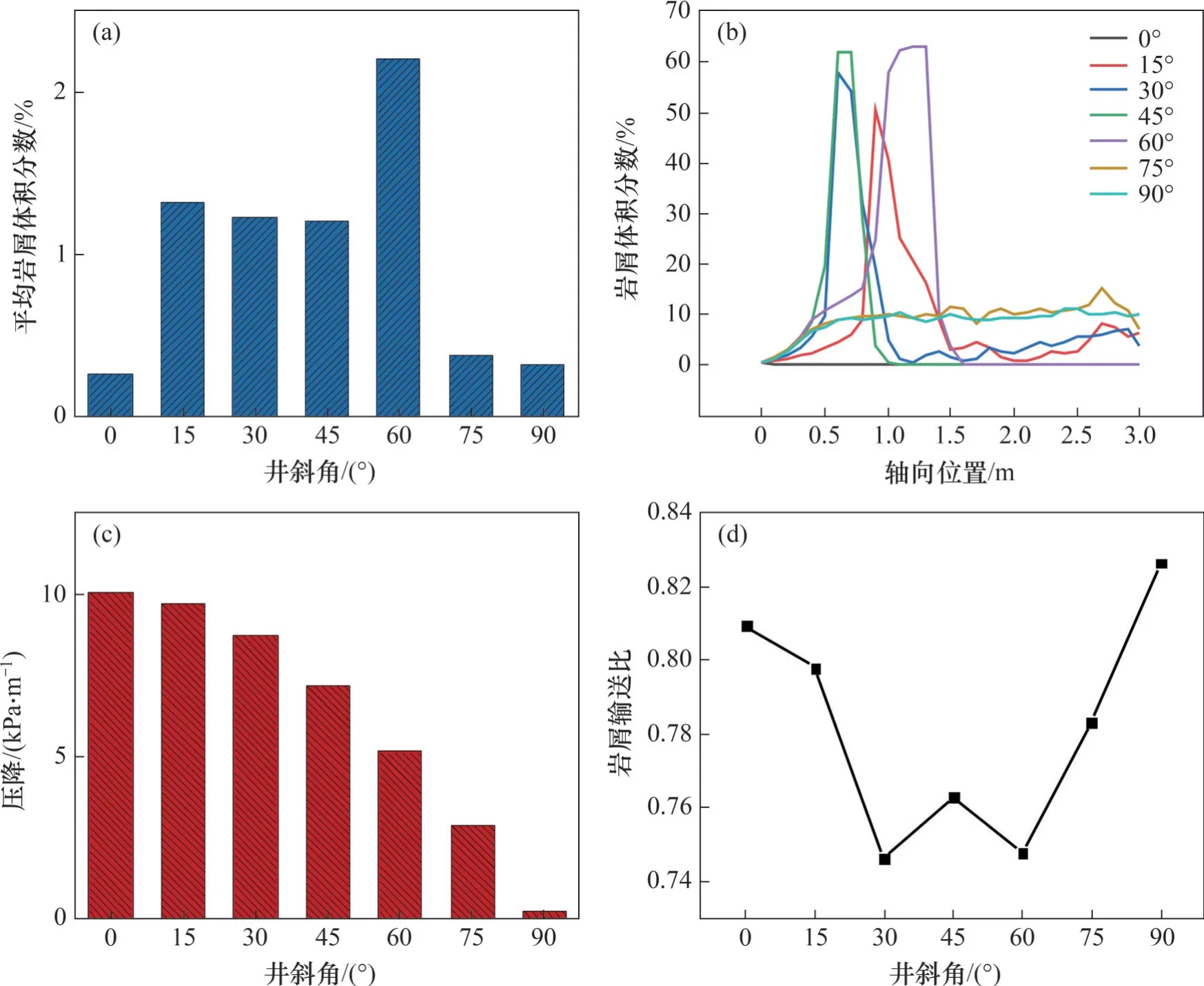
图9 不同井斜角下岩屑体积分数、压降和岩屑输送比分布Fig. 9 Distribution of cuttings volume fraction, pressure drop and cuttings migration ratio at different inclination angles

4.6 钻杆振荡对岩屑运移的影响

本研究主要探究不同振荡幅度及振荡频率下岩屑体积分数和岩屑速度的变化。所采用钻井工况参数为：水平井，无偏心，岩屑初始速度为1 m/s，参考国内外现有振动减阻工具参数，选取钻柱振荡频率范围为5～20 Hz，振幅范围为3～12 mm[25-27]。

不同振荡频率下岩屑速度和岩屑体积分数分布如图10 所示。图10(a)反映了振荡幅度为9 mm时，不同振荡频率下平均岩屑体积分数的变化，可见相比于无振荡工况，钻杆振荡可有效减少环空内平均岩屑体积分数，且随频率增加，岩屑体积分数逐步降低。从图10(b)和(c)可见：当钻柱振荡频率为15 Hz时，岩屑在环空顶部悬浮运移速度及环空底部运移速度均达到最大值，岩屑以移动床和悬浮状态运移至出口，在单位时间内，其携岩数量比其他频率下岩屑的固定床、移动床和悬浮运移模式的多。但钻柱振荡频率为15 Hz时的岩屑体积分数比20 Hz时的略高。经分析认为，钻杆振荡频率越高，对钻杆附近岩屑床的扰动作用越明显，而这种扰动有利于岩屑的二次悬浮，致使部分岩屑能以一定的速度运移出环空，达到降低环空底部固定床高度的效果。

不同振荡幅度下岩屑体积分数和岩屑速度分布见图11。从图11可知：当振荡频率为15 Hz时，随着振幅增加，环空岩屑体积分数特别是钻杆附近区域的岩屑体积分数整体均呈现下降趋势；随着振幅增加至9 mm，环空上部高流速区域的面积逐渐增加，且岩屑速度也达到最大值，这说明振幅为9 mm有助于将颗粒携带至更远的距离。与岩屑运移规律随振荡频率变化规律类似，虽然振幅为 9 mm 的岩屑速度比振幅为12 mm 时的岩屑速度略高，但当振荡幅度为12 mm 时，钻杆的运动对岩屑床的扰动越明显，会在一定程度上降低环空底部的岩屑体积分数，导致岩屑沉降体积分数更低。

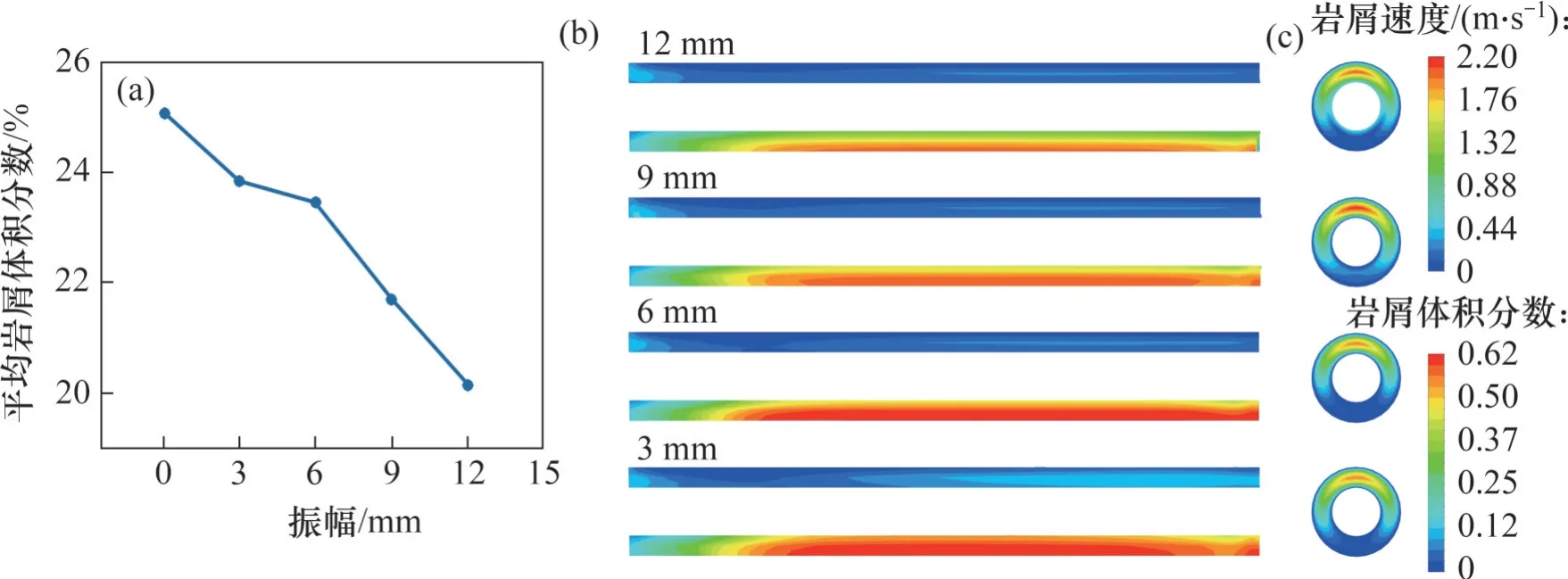
图11 不同振荡幅度下岩屑体积分数和岩屑速度分布Fig. 11 Distribution of cuttings volume fraction and cuttings velocity under different oscillation amplitudes

经综合分析认为，与无振荡工况相比，钻杆的振荡对提高岩屑运移效率有较好的效果，且随着频率及振幅增加，环空内岩屑体积分数均逐渐降低。在岩屑速度和运移模式下，在振荡幅度为15 Hz、振幅为9 mm 的工况下携岩效率最高，在该工况下，岩屑速度达到最大值，并且岩屑以移动床和悬浮模式运移，无固定床存在，致使单位时间携岩数量最高。

5 结论

1) 环空流速增加可以增加对岩屑颗粒的拖曳力，加大岩屑运移速度，降低岩屑体积分数，进而提高携岩效率。

2) 岩屑直径对岩屑运移的影响主要由单个颗粒所受重力以及颗粒碰撞损失控制。在微小井眼运移环境下，当颗粒直径为1.5 mm 时，岩屑体积分数达到最大值。

3) 增加机械钻速不仅能提高岩屑初始速度，而且会使进入环空的颗粒数量增加，导致环空空间内岩屑体积分数升高，故在提高机械钻速的同时，应增加钻井液循环速度。

4) 在偏心状态下，岩屑主要以固定床模式运移，岩屑运移效率明显降低，且随着偏心度增加，岩屑运移过程愈加受阻。

5) 在岩屑运移过程中，井斜角对钻井液携岩效率影响显著。垂直及水平段岩屑运移效率均比倾斜段的高，而在倾斜段中，井斜角为60°时环空内平均岩屑体积分数达到最高值，岩屑运移难度最大。

6) 钻杆振荡可显著提高岩屑运移效率，随振荡频率及振荡幅度增加，平均岩屑体积分数均呈下降趋势，且在流速为1 m/s、振荡幅度为15 Hz、振幅为9 mm的工况下，岩屑运移速率最大。