计及高阶方程分段线性化的港口电-氢综合能源系统优化调度

李立钦，石庆鑫，王月汉，刘文霞，倪建富，何春晖

（1.华北电力大学 电气与电子工程学院，北京 102206；2.国网北京市电力公司朝阳供电公司，北京 100020；3.国电南瑞科技股份有限公司，江苏 南京 211106；4.国富氢能技术装备股份有限公司，江苏 苏州 215637）

0 引言

海洋运输是国际物流中最主要的运输方式，我国进出口货运总量的约90 % 都是通过海上运输的［1］，港口作为连接陆地运输和海洋运输的纽带，每天都会消耗大量的电能和化石能源。例如，宁波—舟山港作为货物总吞吐量世界第一大港口，在2020年全年消耗684 GW·h 的电能和超过80 000 t 的燃油［2］。港口巨大的能源消耗带来了一系列环境问题，如何建立节能与环境友好型港口成为学术界与工业界重要的研究课题［3］。

大多港口地区具有丰富的风力资源和太阳能资源，针对其不确定性和波动性大的特点，国内外学者提出了基于电制气（power to gas，P2G）技术的综合能源系统，以提高新能源消纳率。P2G 技术通过使用电能制取氢气或天然气消纳可再生能源，实现大规模电网的调峰功能［4］。近年来，随着电解水制氢技术成本的逐渐降低，氢动力起重机、氢动力卡车等用氢设备快速发展，在港口地区有广泛的应用前景［3-4］。相较于电转天然气技术，电转氢的化学反应更容易实现，因此，电-氢综合能源系统成为港口地区提高可再生能源利用率的手段之一［5-9］。

目前，国内外学者针对综合能源系统的建模及优化调度已经开展了相关研究。文献［10-12］针对需求响应、风电不确定性等问题，提出一种园区级天然气-电力综合能源系统的日前调度模型，但该模型未考虑P2G和气体存储过程，因此，当可再生能源发电超过负荷需求时，该模型并不适用于港口电-氢综合能源系统。文献［13］针对“双碳”目标下构建清洁低碳安全高效的新型电力系统的要求，从氢储能和风光不确定性2 个角度，构建计及风光不确定性的电-热-氢综合能源系统分布鲁棒优化模型，虽然极大地降低了风光不确定性给系统带来的风险，但对能量转换元件（电解槽）和能量储存元件（储氢罐）的建模过于简化，因此，调度策略无法准确表征港-船多能源融合系统的运行状况。文献［14］针对目前港口地区新能源消纳率低的问题，综合考虑海上风电-氢能系统的多种运行模式，提出引入大容量制储氢设备的系统配置方案，虽然极大地降低了系统碳排放，但仅考虑储氢罐内氢气质量的变化，而没有考虑储氢罐内的温度-压强特性，因此，无法合理约束储氢罐的运行范围。文献［15］为消除负荷不确定性给系统经济运行和主网联络线计划值跟踪带来的不利影响，提出一种包含对负荷反馈修正的电-热-氢综合能源系统多层协调优化策略，对储氢设备的建模考虑了氢气在高压状态下的物理特性方程，但在求解时所采用的麻雀搜索算法不仅易陷入局部最优解，而且求解效率过低。文献［16］针对负荷与新能源出力预测误差大小不同的特点，提出考虑电-气-热-氢需求响应与阶梯式碳排放费用机制的多时间尺度低碳运行优化策略，通过在日前、日内和实时3个时间尺度下协同优化调度有效提升系统的运行优化管理水平，但在求解过程中存在的大量冗余数据降低了系统的求解效率。

综上所述，现有文献大多以源荷不确定性及多时间尺度协同优化调度为切入点，开展对综合能源系统的研究，但较少关注不同运行工况下建模的精确性，具体存在以下两方面问题：对高压储氢罐的建模过于简化，同时较少关注氢气在高压状态下的物理特性；实际工程对系统的求解效率要求很高，需要在保证系统建模精确性的前提下有效缩短求解时间。

针对以上问题，本文提出考虑电解槽和储氢系统精细化建模的港-船综合能源系统日前调度策略，主要创新点为：基于范式修正系数，建立储氢罐内氢气在高压状态下的物理特性方程，准确刻画氢气的物理状态，保证系统安全稳定运行；考虑到在单时间步长内系统求解时间不宜过长，本文在一定误差允许范围内对氢气物理特性方程这一强非线性约束进行分段线性化处理，极大地提高了模型的求解效率。

1 电-氢综合能源系统建模

考虑到园区输气管道距离较短，本文将港口电-氢综合能源系统建模为包含风能、太阳能及氢气制取和储存单元在内的能源集线器模型［14-15］，如图1所示。

图1 港口电-氢综合能源系统框架Fig.1 Framework of electricity-hydrogen integrated port energy system

该系统虽然接入了上级电力系统，但主要由包括风电机组和光伏发电板在内的新能源供应。负荷包括电负荷与氢负荷。当新能源发电不能满足电负荷需求时，港口地区将会从上级电力系统购电；类似地，当该系统制取的氢气不能满足港口氢负荷需求时，港口地区将会从外部购取氢气。该系统主要包括以下部分。

1）发电部分。该部分包括大规模风电机组和光伏发电系统。本文假设港口地区风电出力和光伏出力被充分利用，即无弃风弃光现象。

2）能源转换部分（电解槽）。相较于氢站中恒功率运行的电解槽，该系统中的电解槽功耗可以随着新能源出力和负荷需求的波动而变化。

3）储氢部分。目前最成熟、最经济的储氢方法是将制取的氢气经过压缩机压缩后注入高压储氢罐中进行存储［17］。

4）氢负荷部分。该系统中的氢负荷包括氢动力卡车、起重机以及船舶［18］。

5）电负荷部分。该系统中的电负荷包括灯光系统和空调系统在内的常规港口负荷、氢气压缩机以及停泊船只电负荷［7］。

1.1 风电机组与光伏发电系统模型

风电机组通过叶轮和同步发电机将风能转化为电能，其出力取决于实时风速与风机出力特性曲线，计算公式［19］为：

式中：P为t时刻风机实际输出功率；P为风机额定输出功率；vw，t为t时刻叶轮所处高度区间的风速；vci为风机切入风速；vr为风机额定风速；vco为风机切出风速。本文假设风机是不可调度的电源，始终在最大功率点运行。

对于光伏发电系统，假设光伏逆变器的控制策略可保障光伏组件在最大功率点运行，功率输出与正常范围内的太阳辐照度成正比。在额定功率范围内，一个光伏组件的输出功率与光伏板法向入射辐照度成正比［20］。光伏发电系统的输出功率P计算公式为：

1.2 电负荷

港口地区需要消耗大量的电能用于照明、空调、起重机、停泊船供电等。电力负荷由两部分组成，即：

式中：P为t时刻港口基础设施总负荷；P为t时刻船舶功率总需求。一般而言，P包括照明、监控和空调设备负荷，可以根据港口日常活动进行估计，P可根据船舶使用岸电的行为进行估计，因此，在船舶靠泊时间表与港口生产行为已知的情况下可以相对精准地预测电力负荷曲线。

1.3 电解槽

1.3.1 碱性水电解槽的产氢出力特性

电解槽是一种通过电解反应消耗电能产生氢气的装置。制氢电解槽分为碱性水电解槽、聚合物电解质膜电解槽和固体氧化物电解槽3 种类型。其中，碱性水电解槽技术简单、成熟，易于操作，因此更适用于大规模产氢［21］。

大型电解系统由一组电解槽阵列组成，反应生成的氢气被储存在高压储气罐中备用，而生成的氧气则由另一个储气罐收集。以碱性水电解槽为例，其运行原理如图2 所示，电解槽的控制系统包括电流控制器、温度控制器、气体压力控制器和液位控制器。碱性水电解槽中的总产氢速率GHt与提供给反应堆的直流电流呈线性关系［22-23］，可表示为：

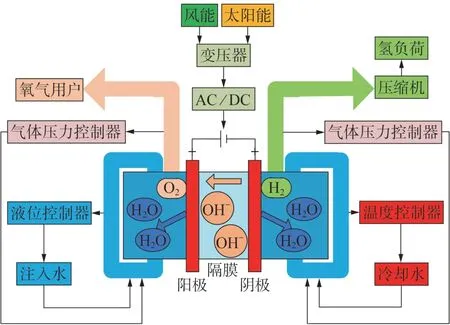
图2 碱性水电解槽的结构和控制模块Fig.2 Structure and control blocks of alkaline water electrolyzer

式中：ηF为法拉第效率，是实际产氢量与理论产氢量之比，与电解温度密切相关；Nce为电解槽阵列中的电解槽数量；Ice，t为t时刻流过电解槽单元的电流；ze为反应中转移电子的摩尔数，氢气的ze为2；F为法拉第常数。在港-船综合能源系统中，式（4）应表示为产氢率与电能消耗之间的相关性。交流／直流变换器可以保持一个恒定的终端电压Vce，同时调节电解槽流过的电流Ice，电解槽经济耗电量PEY计算公式［21］为：

因此，总产氢速率可以用电能消耗来衡量，即：

式中：AEY为电解槽的产氢系数，如式（7）所示，单位为kg／（kW·h）；P为t时刻电解槽的耗电量。

以额定功率为1 kW、效率为74 % 的电解槽为例，该电解槽每小时可产生0.018 7 kg（9.37 mol）氢气［8］。上述分析表明，电解槽的总产氢速率与耗电量成正比。系数AEY只适用于特定的电解液温度。在不同的温度条件下，法拉第效率可以用经验公式进行估计，即：

式中：a1—a7为经验系数；Te为电解液温度；Temax、Temin分别为电解液的最高运行温度和最低运行温度；ρI为电解槽电流密度。在正常范围内，电解液温度越高，则法拉第效率越高。实际运行中，温控装置可以将电解液温度维持在70～90 ℃［21］。

1.3.2 碱性水电解槽的运行约束

电解槽的控制模块如图2 所示，包括压力控制器、液位控制器和温度控制器［24］。一般情况下，港-船综合能源系统调度的时间间隔在0.5 h 内，应考虑爬坡约束。由于碱性水电解槽的动态过程较慢，其功率爬坡和滑坡限制［25］为：

式中：U为二元变量，其值为1，表示电解槽处于运行状态，为0 表示电解槽处于停机状态；P为电解槽最大功率；RU、RD分别为功率爬坡上限和功率滑坡上限；M为一个充分大的正数。

1.4 氢气压缩机和储氢罐

氢气在高压下储存在储氢罐中。氢气压缩机从电解槽中吸收低压氢气，并将高压氢气注入储氢罐中备用。

1.4.1 氢气压缩机

氢气压缩机的功耗与压缩比有关，压缩比由储氢罐内气体的目标压力决定。根据经验方程，氢气压缩机的功率消耗P为：

式中：CH为氢气比热容常数；Tin为注入压缩机的氢气温度；KH为氢气的等熵指数，(KH-1)/KH等于0.286［17］；ηCM为氢气压缩机的运行效率；F为t时刻压缩机的输出气体压力；Fin为压缩机的输入气体压力；F、F分别为气体压力的上、下限。式（12）中G、F为决策变量。为简化求解，根据氢气压缩机的工作压力范围，将式（12）近似转换为式（14）。

1.4.2 储氢罐

储氢罐的热传导模型是港口综合能源系统建模的难点。在给定最大承受压强的条件下，需要通过计算储氢罐的气体温度范围判定其储氢质量。然而，在较高的气压下，气体温度、压强与物质的量的关系呈现高阶非线性，且无法在某个运行点附近进行线性化处理，因而求解计算量大。

本文通过一阶热传导模型估算储氢罐内氢气稳态温度值，进而将罐体热传导模型进行化简后代入整个模型中。

当储氢罐内氢气压强高于8 MPa 时，氢气的温度-压强特性可用范式方程刻画［28-29］，即：

当储氢罐内氢气压强低于8 MPa 时，储氢罐内氢气的物理特性方程为：

由式（15）可知，在稳态条件下，储氢罐内氢气压强取决于氢气的温度与物质的量。本文所建立的优化调度模型时间尺度为0.5 h，根据储氢罐的热传导模型可知，当进气速率根据调度决策突然变化时，储氢罐内氢气的温度在1～2 min达到稳态值，因此在优化调度模型中不必考虑氢气质量变化时的动态过程，而只需要计算储氢罐内部氢气稳态温度，其计算公式（详细推导过程见附录A）为：

式中：RSTK为储氢罐罐壁的热阻；G为t时刻进气速率，其计算公式如式（18）所示；θin为储氢罐入口处氢气的温度；θf为储氢罐外部环境的温度。

储氢罐的运行约束［26］为：

式中：G为t时刻从港口地区外部购买的氢气；G、G分别为t时刻充、排氢速率；G、G分别为最大充、排氢速率；γTK为储氢罐泄漏率；S为t时刻氢气存储量；ηdis为考虑气体耗散的储氢罐储存效率；F为t时刻储氢罐入口处压力。式（18）表示购买的氢气和电解产生的氢气都通过氢气压缩机进入储氢罐；式（19）、（20）分别表示气体充、放速率约束；式（21）反映储氢罐内氢气量的变化量；由于氢气压缩机输出的氢气直接进入储氢罐中，2 台设备的气体可联通，式（22）表示氢气压缩机的输出压力等于储氢罐入口处压力。

1.5 氢负荷

氢气既可以供应牵引载荷，如氢动力起重机或卡车，也可以供给氢动力船舶［7］。氢气从储氢罐注入用氢负荷，注氢时间计划可以由港口运营商预测，因此G计算公式为：

式中：N为氢负荷总数；D为t时刻第j个接入 储 氢罐内的氢负荷。

1.6 经济调度策略

港-船综合能源系统的日前调度目标函数为系统的运行成本最小化，即：

式中：WT为系统经济调度的时间集合；Δt为经济调度的时间步长，本文中，港-船综合能源系统日前调度的时间步长为0.5 h；、分别为t时刻从市场购电和购氢的单位费用；为t时刻的购电功率。

为简化系统模型，本文松弛了港口地区氢气管道传输容量约束，因此，不需要考虑电网中的电压降和氢气管网中的气体压力损失，将港-船综合能源系统简化为一个基于能量集线器的系统。此外，本文将系统中可能存在的多个电解槽和储氢罐等效为1 个容量更大的电解槽和储氢罐。因此，综合能源系统的供电包括风电机组出力、太阳能机组出力以及从外部系统购买的电能，耗电包括电解槽耗电、压缩机耗电以及电负荷。电力平衡方程为：

2 电-氢系统模型的分段线性化

在电-氢综合能源系统中，储氢罐内氢气在高压状态下的物理特性方程这一高阶非线性模型严重影响了电-氢系统模型的求解效率，这是因为：传统的分段线性化方法大多针对2 个变量的耦合关系式，而该方程为压强、物质的量、温度3 个变量耦合的方程，增加了变换的难度；该方程中氢气物质的量最高为三次方，这增加了分段线性化的计算量，影响了求解效率。针对上述问题，本文提出高阶非线性约束的分段线性化方法。

2.1 改进思路

式（15）为多变量耦合的高阶非线性方程，无法直接采用传统的分段线性化方法进行处理。本文通过变量转换的方法将原方程转化为2 个变量之间的高阶方程。由于直接对所得方程进行分段线性化时的求导计算量过大，因此，本文对该方程进行多项式拟合后再对拟合结果进行分段线性化处理。

2.2 储氢罐内氢气物理特性的改进

将式（17）和式（21）代入式（15）中，可得：

式中：f(⋅)为函数关系式。

再对得到的关系式进行二次曲线拟合，可得：

式中：A、B、C为储氢罐内氢气压强参数。由于储氢罐内氢气质量受上一时刻储氢量这一状态变量的影响，因此，在不同时刻所得到的压强-进氢速率关系式有所差异，储氢罐内氢气压强参数A、B、C在该调度模型中为状态变量。

可利用式（28）—（30）进行分段线性化处理。

3 仿真验证

本章对所提电-氢综合能源系统优化调度模型进行算例分析。在一台配备英特尔酷睿i7 处理器（2.80 GHz）和16 GB RAM 的个人电脑上进行仿真，代码通过基于MATLAB 的IBM ILOG Gurobi Optimizer version 10.0.0 实现。整个优化调度模型为混合整数规划问题，可以直接利用Gurobi 求解器进行求解。

3.1 系统描述

港口电-氢综合能源系统框架图如图1 所示。港-船综合能源系统的部件参数如附录C表C1所示。一天中风电机组出力和太阳能机组出力如附录C 图C1 所示。图3 为一天中电负荷和氢负荷的预测结果。一天中不同时间的分时电价曲线如附录C 图C2 所示。本文中购氢价格在一天中保持不变。考虑到风电机组和太阳能机组出力的不确定性，本文以0.5 h 为一个时间步长，求解使日内累计成本最小的调度决策。

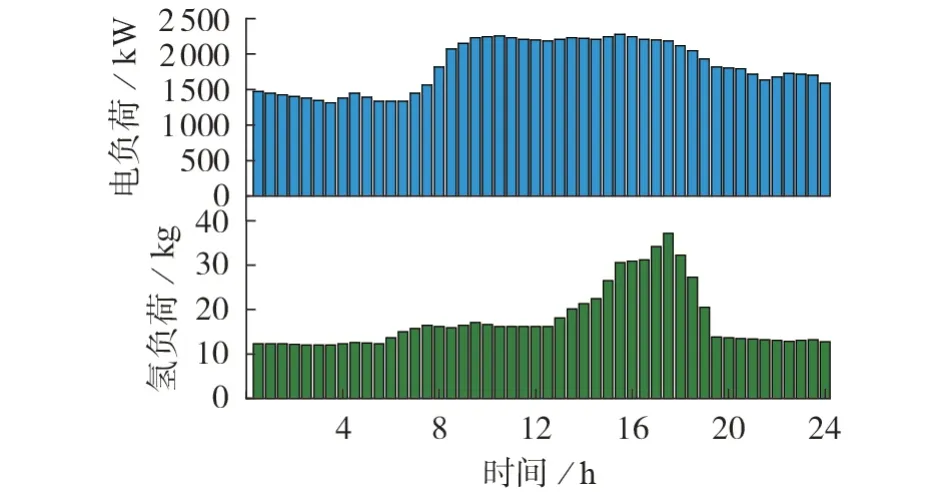
图3 一天中电负荷和氢负荷的预测结果Fig.3 Forecasting results of electriticy and hydrogen load in one day

3.2 仿真结果

基于本文最优调度方法求解综合能源系统的调度计划。电能、氢能调度方案分别如图4（a）、（b）所示，图中纵轴正值部分表示能量输出，负值部分表示能量需求。储氢罐荷电状态、储氢罐内氢气的物理特性分别如图5（a）、（b）所示。电-氢综合能源系统单时间步长成本以及累计成本如附录C图C3所示。

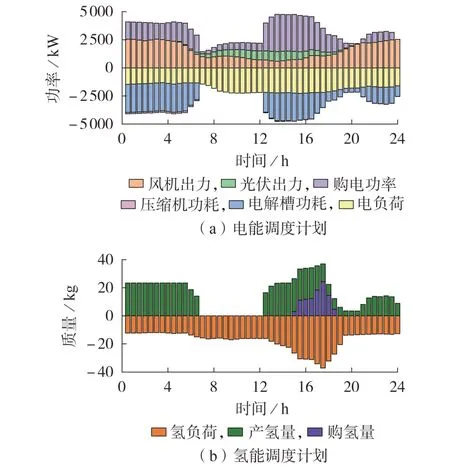
图4 综合能源系统调度计划Fig.4 Scheduling plan of integrated energy system

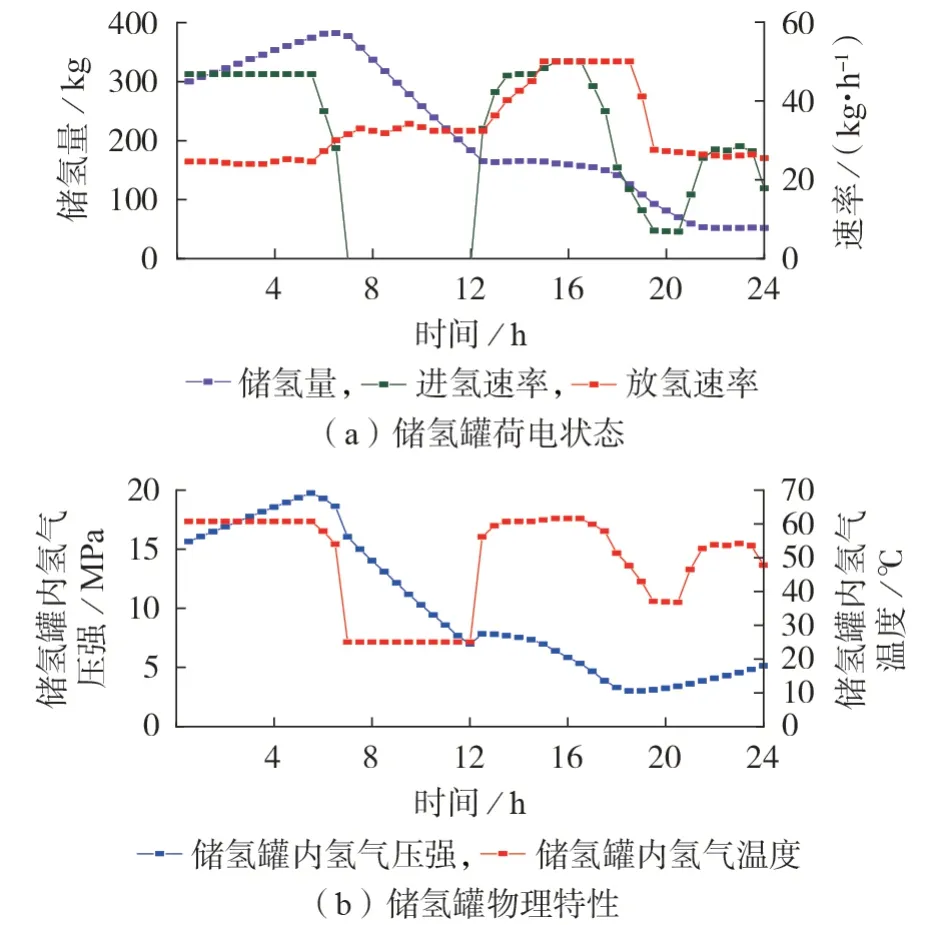
图5 储氢罐运行状态Fig.5 Operating state of hydrogen storage tank

图4 中，夜间风电机组出力大于电负荷需求，因此剩余电力被用于产生氢气来供应氢负荷。在第一个电价低谷期（0 — 6 h），决策者为降低该系统日内累计成本，选择从上级电力系统购电来增加电解槽的产氢量；在第二个电价低谷期（11 — 17 h），新能源机组出力不能满足电负荷需求，决策者选择通过购电来满足负荷需求。此外，由于购氢价格昂贵，港-船综合能源系统增加购电量并将其通入电解槽产生氢气以供应氢负荷，而不是直接购买氢气。然而，在15 h 时，储氢罐内氢气储存量过低，压强达到下限，为满足用氢设备的后续需求，决策者开始从系统外部购买氢气，重新启动电解槽来供应氢负荷，此时系统的运行成本开始大幅增加。

图5 中，在对储氢罐内氢气压强施加上、下限约束后，储氢罐内氢气质量和温度都得到了有效控制，这使储氢罐工作在安全稳定运行范围之内。

为说明P2G 设备对系统新能源消纳能力、削峰填谷能力以及运行费用的影响，本文设置以下3 个场景进行对比分析：场景1，不考虑P2G 设备，电负荷由风电机组、太阳能机组供电，电、氢负荷缺额部分从外部电力系统购买；场景2，不考虑P2G 设备，系统中加入蓄电池组，可以将新能源出力剩余部分储存在蓄电池组中，电、氢负荷缺额部分从外部电力系统购买；场景3，考虑P2G 设备，新能源机组出力剩余部分通过电解水制氢系统进行储存，以供应氢负荷，电、氢负荷缺额部分从外部电力系统购买。

不同场景下系统的各项成本及总成本如表1 所示。由表可知：相较于场景3，场景1 不考虑储能设备，弃风弃光成本大幅增加，场景2 考虑蓄电池组，虽然在一定程度上降低了弃风弃光成本，但由于没有考虑P2G 设备，购氢成本依然很高；场景3 考虑P2G 设备，由于购电成本低于购氢成本，因此在该场景下选择在电价低谷期从外部电力系统购电来制取氢气，并将其储存在系统中以应对后续时段的氢负荷，虽然购电成本增加，但购氢成本、弃风弃光成本及总成本得到显著降低，这证明本文所提调度方案具有更好的综合优化效果。

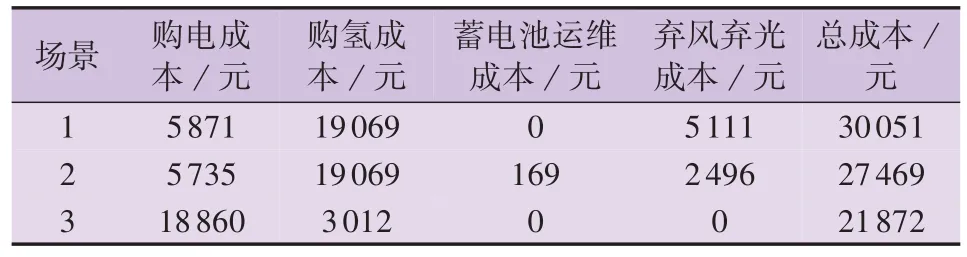
表1 不同场景成本对比Table 1 Cost comparison among different scenarios

3.3 分段线性化误差分析

为验证所提储气罐物理特性分段线性化模型的实际效果，本文将氢气物理特性的不同模型分别代入港口电-氢综合能源系统中，不同模型结果对比如表2 所示。表中：线性模型的物理特性方程表达式如式（16）所示，利用线性求解器对其进行求解；非线性模型的物理特性方程表达式如式（15）所示，直接利用非线性求解器对其进行求解；改进模型的物理特性方程是在式（15）的基础上，通过式（26）—（30）进行分段线性化处理的方程，利用线性求解器对其进行求解；相对误差为各模型结果相对非线性模型结果的误差。

表2 不同模型结果对比Table 2 Results comparison among different models

不同模型下的储氢罐内氢气压强及相对误差如图6 所示。由图可知：当储氢罐内氢气压强升高时，线性模型所反映的氢气物理特性精确性远低于改进模型；线性模型得出的储氢罐内氢气压强远低于实际值，这导致当系统内氢气压强达到上限时，由线性模型求解出的压强还未达到临界值，决策者会继续注入氢气，进而影响系统的安全稳定运行。

由表2、图6 可知，储氢罐内氢气物理特性的改进模型在误差允许范围内极大地提高了电-氢综合能源系统模型的求解效率。

综上所述，本文所提港-船综合能源系统调度方法在分时电价的条件下，协调了电能和氢能系统的运行，同时在保证建模精确性和求解效率的前提下，实现了港口电、氢负荷供能成本最小化。

4 结论

针对高比例新能源接入港口微电网的场景，本文提出一种基于能源集线器的港口电-氢综合能源系统模型，该模型包括新能源机组、制氢、储氢以及氢／电负荷等多种元件的稳态模型。针对现有研究中储氢系统建模不精确的问题，本文基于范式修正系数建立氢气在高压状态下的物理特性方程。同时，考虑到实际工程对求解效率的要求，本文对储氢罐的物理特性方程进行分段线性化处理，提出一种储氢罐内氢气物理特性的改进模型，并在此基础上，建立日前最优调度模型。通过对比不同模型对系统调度结果的影响，验证了本文所提改进模型在保证建模精确性的前提下，提高了系统对新能源发电的消纳能力，从而降低了港口的碳排放。

未来笔者将对港口综合能源系统进行更全面的建模，并将对氢负荷的物理模型进行更深入的研究。

附录见本刊网络版（http：//www.epae.cn）。