斜直组合桩支护深基坑开挖滑动面分析
吴 鹏 崔佳浩 罗志春 邱红胜 周亦辉
(1.湖北省路桥集团有限公司 武汉 430056; 2.武汉理工大学交通与物流工程学院 武汉 430070)
在进行深基坑开挖时,势必会导致基坑周边土体的应力场和位移场发生改变,继而对基坑附近结构产生影响,使临近结构出现明显变形,严重时甚至会导致临近结构破坏[1-2]。我国城市建设的飞速发展过程中出现了大量的深基坑工程,深基坑施工影响临近结构安全性的问题日益突出[3-4]。
梁发云等[5]使用两阶段法winkler地基模型分析了受基坑开挖引起土体水平位移作用下单桩的受力变形性状。而使用其求解临近桩基因基坑开挖所产生的位移时的一个前置条件为:对基坑开挖所产生的滑动面进行分析,得出临近桩基的边界条件。因此,对斜直组合桩支护深基坑开挖滑动面进行分析十分必要。
传统基坑稳定性分析常使用圆弧滑动法,认为圆弧滑动法的破坏形式主要为围护结构绕坑底旋转破坏。但圆弧滑动法不适用于围护结构嵌固深度较小的基坑工程,传统圆弧滑动法中滑动面始终通过桩底这一假定并不合理,圆弧滑动法滑动半径如何确定也值得研究。
同时,当基坑坑底以下为软土地基时,传统基坑稳定性分析常假定坑底软土层强度均匀分布,使得分析结构中,破坏面深度过大,且覆盖整个坑底,与实际情况不符。
本文采用有限元法对软土地基基坑破坏滑动面进行研究,研究基坑开挖深度、支护结构插入比和土体强度等条件对基坑隆起破坏滑动半径的变化规律的影响,以期得到基坑滑动面分析时滑动半径选取范围的建议。
1 工程概况
1.1 地质概况
施工场地位于湖北省武汉市某深基坑工程,地貌属河流冲积平原。基坑开挖10 m,土体分层和各项参数及取值[6]见表1。

表1 土体参数及取值
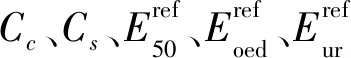
1.2 现场施工方案
本基坑工程在枯水期施工,稳定地下水位为14 m,施工期间降水次数和降雨量较小,基坑排水方法为明沟排水,地下水对基坑工程影响不大,地下水仅改变了土体的有效重度,不考虑水流固结耦合作用。
根据施工要求,基坑开挖深度为10 m。一面采用前排倾斜桩加后排直桩的斜直组合支护桩支护,支护方式见图1~图3。
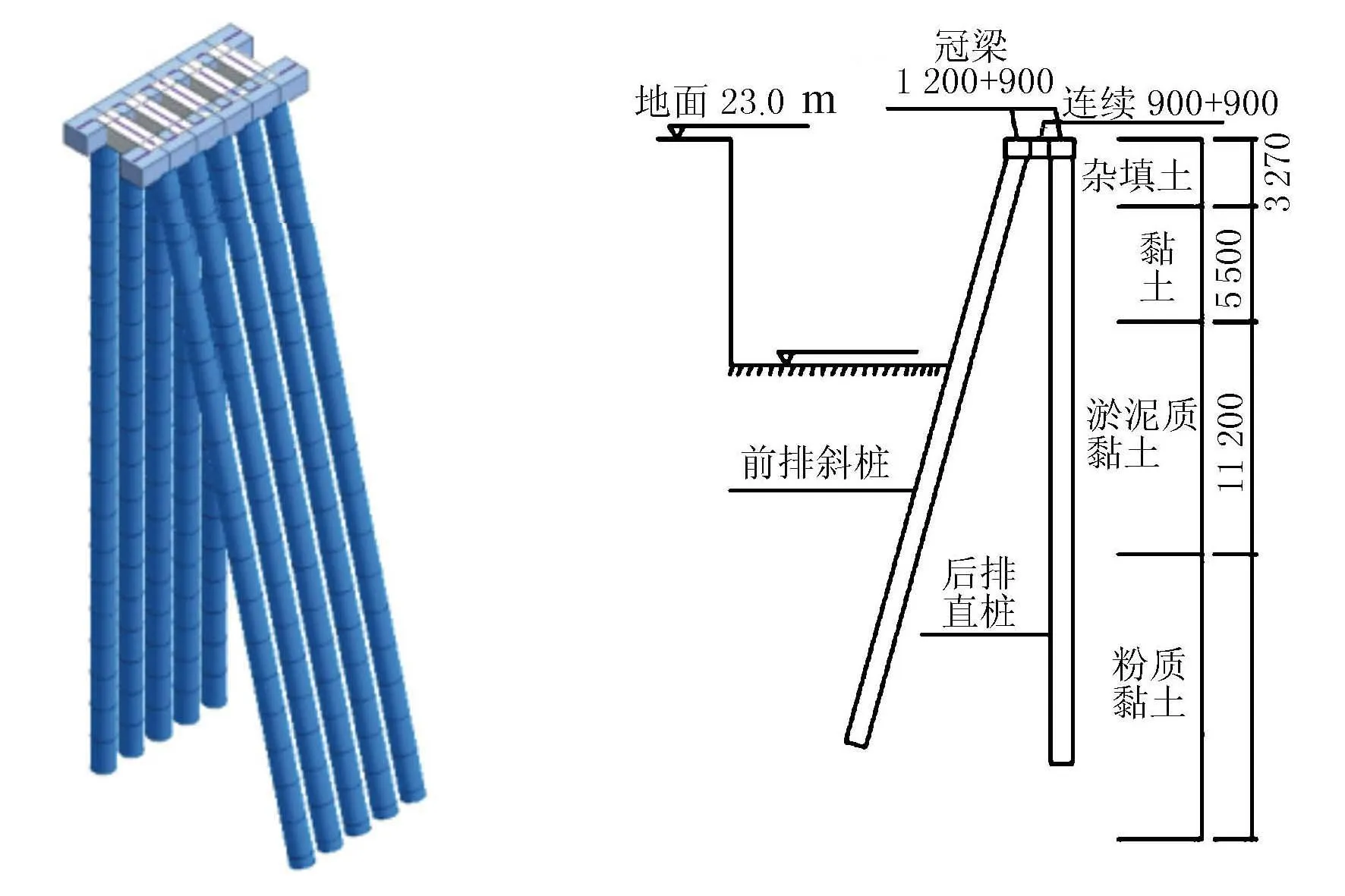
图1 双排桩示意图图2 基坑剖面图(尺寸单位:mm)

图3 基坑支护几何模型
2 数值模型及参数
2.1 模型建立
采用有限元计算软件midas GTS NX建立45 m×45 m基坑的三维空间模型,模型宽度取3倍基坑宽度,宽度130 m,模型高度取7倍开挖深度。土体模型采用修正剑桥-黏土模型,考虑不排水抗剪强度沿深度线性增长。桩身与连梁冠梁均采用弹性模型,不考虑地下水的影响,建立有限元模型。三维双排桩系统深基坑开挖模型共划分57 822个单元,整体模型网格示意图见图4;双排桩系统深基坑开挖模型见图5。

图4 三维有限元模型
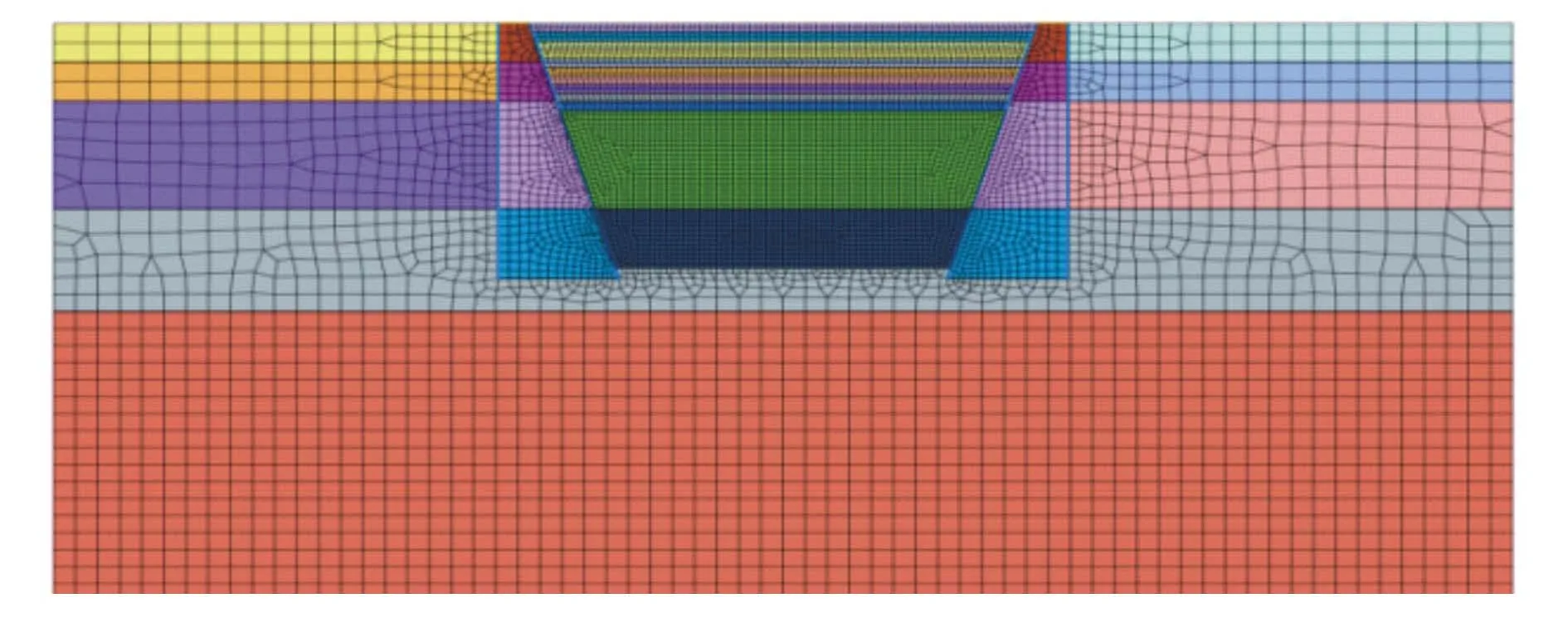
图5 深基开挖有限元模型
2.2 位移计算对比分析
根据排桩位移的监控方案,沿桩身竖直方向,间隔1 m布置测点用于监控桩身的水平位移。基坑施工过程中,间隔1 d读取监测数据,斜直组合支护桩深基坑开挖10 m后依据现场监测数据,待基坑变形稳定后,绘制20号桩位的前排斜桩和后排直桩水平位移监测结构见图6、图7。
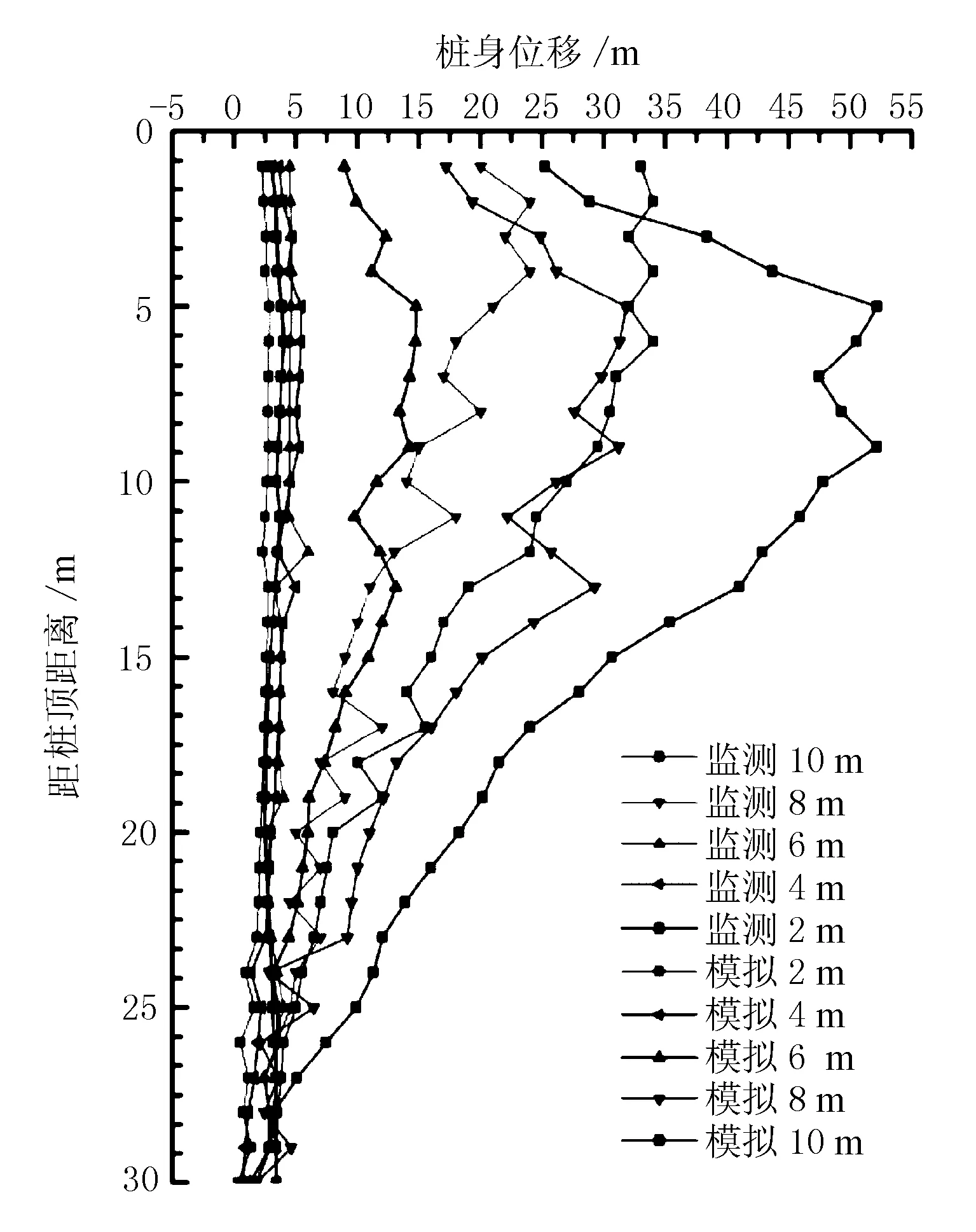
图6 后排直桩桩身位移

图7 前排斜桩桩身位移
根据现场排桩位移的监控方案,对数值模型进行验证,采用与现场试验相同的施工方式。模拟结果见图6,图7。
模型计算结果与实际检测结果对比表明,桩身位移随排桩深度呈先增大后减小的趋势;开挖深度越大,桩身位移增大的速率越大,桩身最大位移发生在距桩顶8 m(桩长27%)处。与实际监测结果对比,有限元模拟结果的变化趋势与实际结果一致,但监测位移小于模拟位移。考虑原因为现场施工速度较快,读取监测结果时土体内部应力尚未平衡,土体变形仍在继续。但仍可认为有限元模拟结果可靠。可用于后续的分析。
3 滑动面形态分析
在传统圆弧滑动法中,常假定土体滑动破坏面始终通过支护结构嵌固端底部,但大量实际工程数据表明这一假定并不合理,基坑滑动破坏面的发展与支护结构的嵌入深度密切相关。为研究基坑滑动破坏面的发展程度与支护结构嵌入深度的关系,假定有某斜直组合支护深基坑工程施工,支护结构斜桩倾角为15°,土体参数见表1,基坑开挖深度为10 m。定义D/H为围护结构插入比。使用有限元模拟分析,支护结构嵌入深度不同时,基坑滑动破坏面见图8。其中:H为基坑开挖深度,D为围护结构嵌入深度。借此研究斜直组合支护深基坑开挖过程中,围护结构插入比D/H对基坑坑底滑动面半径的影响。

图8 不同D/H下土体位移图
由以上有限元模拟结果可知,基坑滑动面的发展与支护结构的嵌入深度密切相关。同时根据支护结构的嵌入深度的变化,可将基坑滑动面的发展分为4个阶段。
1) 支护结构嵌入深度从0开始增加,地基土的破坏滑动面显著深于支护结构嵌固段,如图8a)所示。
2) 地基土的破坏滑动面在支护结构下端附近。
3) 地基土的破坏滑动面恰好经过支护结构嵌入部分的最下端,如图8b)所示;将此时对应的支护结构嵌入深度称为临界嵌深,此时的插入比为临界插入比(D/H)。
4) 如图8c)所示,土的破坏滑动面不再出现在嵌固段下端,而是出现在其中下部;嵌固段下部土体滑动面基本不再改变。
由此可以得出结论,传统圆弧滑动法中,假定土体滑动面始终通过支护结构嵌固端底部并不合理。
3.1 有限元模型验证
使用DLO法(不连续布局优化法),借助LimitState GEO软件,引入软土地基中,土体不排水抗剪强度沿深度线性增长这一条件。实现在软黏土地基中,使用斜直组合桩支护的深基坑开挖过程中,基坑坑底隆起和坑外土体滑动破坏面的研究。
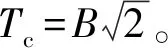
需注意,黄茂松等[7]认为合理考虑支撑的作用,假定支护结构不发生水平位移,即不考虑坑外土体滑移,仅考虑坑底土体隆起。有相同条件下DLO法和强度折减弹塑性有限元法(SSRFEM法)基坑安全系数随Tc/T变化规律见图9;图9所进行的对比分析验证了使用DLO法进行基坑稳定性分析时的可靠性。

图9 安全系数对比图
3.2 土体强度增长率对临界插入比影响分析
当基坑坑底为软土地基时,传统基坑稳定性分析常假定坑底软土层强度均匀分布,与天然软土地基强度常表现出强烈的非均匀性的实际情况不符;由于土体不排水抗剪强度的不均匀性会限制破坏面向下发展,假定坑底软土层强度均匀分布会使得分析结果中破坏面深度过大;故在对坑底土层为软土的基坑进行稳定性分析时,须考虑土体强度的非均匀性,即土体不排水抗剪强度随深度的增加而增加。
由上述分析可知,在软土地基中,基坑外土体的潜在滑动破坏面影响范围也受到软土地基中硬土层埋置深度的影响;当硬土层较浅时,基坑开挖所引起的破坏区域范围会受到硬土层的约束。故本节假定土体软土层厚度无限大和有限元模型土层结构一样,使用LimitState GEO软件对基坑滑动面进行分析时,考虑到支护结构的屈服破坏,取围护结构塑性破坏弯矩Mp=2 000 N·m/m;取前排斜桩倾斜角为15°。研究斜桩倾斜15°的斜直组合双排桩支护软土地基深基坑工程中,在不同开挖深度下,初始土体排水抗剪强度Su0和土体强度增长率对基坑工程临界插入比(D/H)0的影响,其结果见图10。
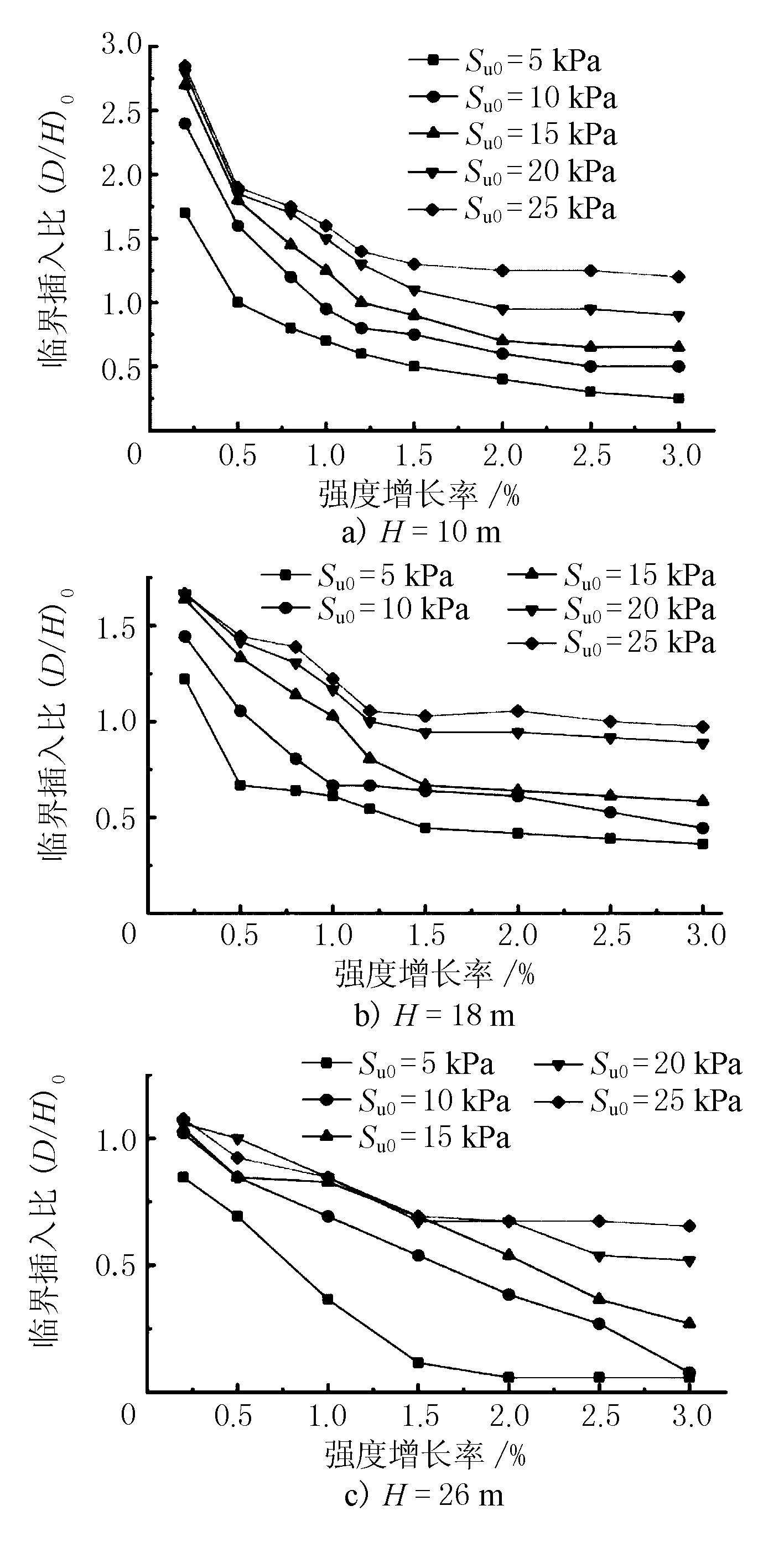
图10 不同开挖深度和初始土体不排水抗剪强度下
由图10可知:
1) 当基坑开挖深度H和土体增强率λ相同时,土体初始不排水抗剪强度Su0越小,围护结构临界插入比(D/H)0越小,即滑动面通过围护结构底端所需的临界插入比越小。
2) 当H和Su0相同时,λ越大,围护结构临界插入比(D/H)0越小,即临界插入比越小。
3) 当λ和Su0相同时,基坑开挖深度H越大,围护结构临界插入长度D增大,插入比(D/H)0减小。若围护结构插入比大于临界插入比,即D/H≥(D/H)0,基坑土体滑动破坏面通过支护结构嵌固端,出于偏安全考虑,计算基坑开挖安全系数和对坑外桩基的影响时,可认为坑外土体滑动破坏面恰好经过围护结构底部,取基坑底部至支护结构底部的距离为滑动面滑动半径。反之,滑动半径需另行确定。
3.3 曲线拟合
为方便在实际基坑工程中根据Su0和λ确定前斜后直组合桩围护结构的临界插入比,可对上述有限元模拟结果进行数据拟合,其拟合方程式为:y=a·xb,其中:y为临界插入比(D/H)0,x为土体强度增长率λ,得出不同土体初始强度Su0下的拟合方程。
3.3.1H=10 m时拟合曲线
基坑开挖10 m时,对不同初始强度下临界插入比随土体强度增长率变化曲线见图11。

图11 H=10 m时拟合曲线
在统计学中可利用R2(COD)和残差平方和(SSE)对拟合结果进行评价,且一般认为R2大于0.8的曲线拟合结果较好。
(2)
H=10 m时,拟合曲线的残差平方和(SSE)和R2(COD)的计算结果见表2,其中残差平方和趋近于0,R2大于0.8,趋近于1。表明H=10 m时的5条拟合曲线结果均较好。

表2 H=10 m时拟合方程评价参数计算结果
由图11可知,实测值与预测值之间存在误差,当预测值大于实际值时,使用预测值进行施工设计仍是偏安全的;对部分实测值大于预测值的点位,其所处曲线和具体数值(取3位有效小数)见表3。
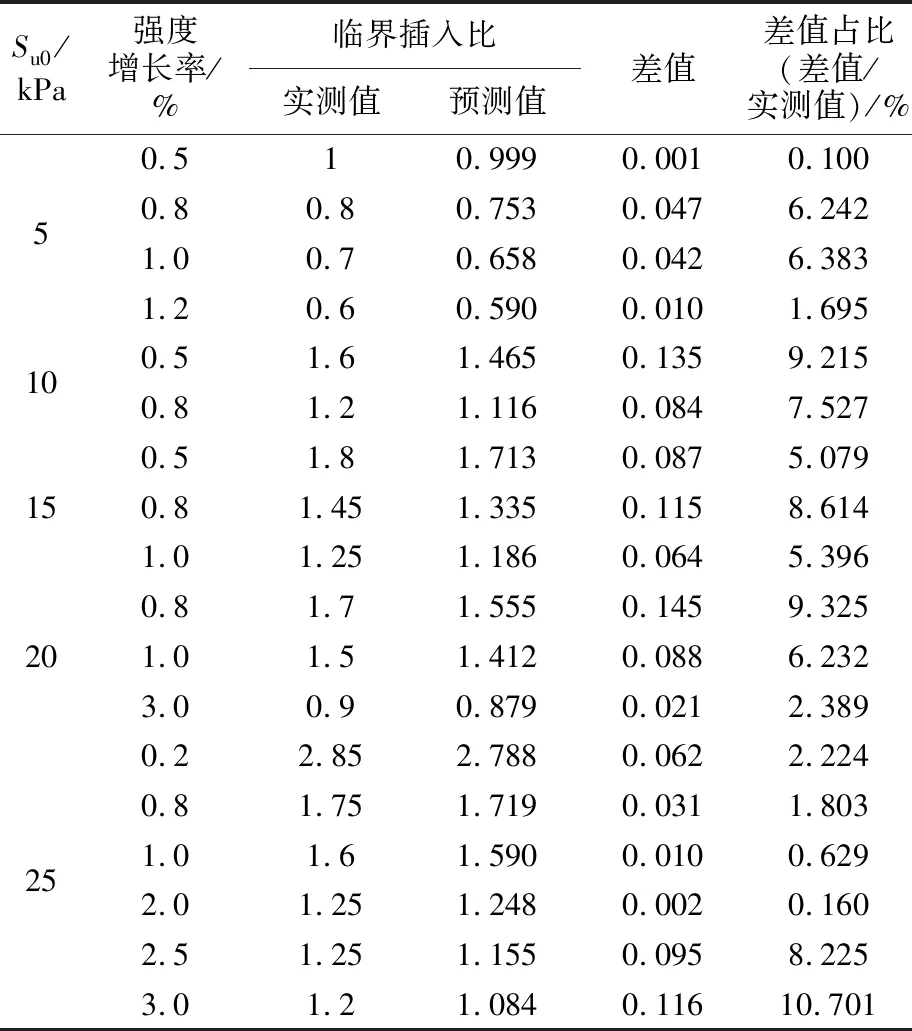
表3 实测值大于预测值点位的数值分析
由表3可知,2种临界插入比的差值与预测值的比值均小于15%,在实际基坑工程中,出于偏安全的考虑,可取1.15的安全系数,将预测值放大后使用。
3.3.2H=18 m时拟合曲线
基坑开挖18 m时,不同初始强度下临界插入比随土体强度增长率变化曲线见图12。
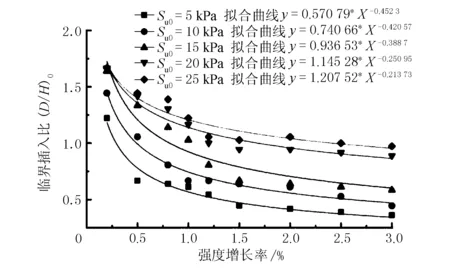
图12 H=18 m时拟合曲线
H=18 m时,拟合曲线的残差平方和(SSE)和R2(COD)的计算结果见表4,其中残差平方和趋近于0,R2大于0.8,趋近于1。表明H=18 m时的5条拟合曲线拟合结果均较好。

表4 H=18 m时拟合方程评价参数计算结果
同样,对部分实测值大于预测值的点位,其所处曲线和具体数值(取3位有效小数)见表5。

表5 实测值大于预测值点位的数值分析
由表5可知,2种临界插入比的差值与预测值的比值均小于15%,在实际基坑工程中,出于偏安全的考虑,可取1.15的安全系数,将预测值放大后使用。
3.3.3H=26 m时拟合曲线
基坑开挖26 m时,不同初始强度下临界插入比随土体强度增长率变化曲线见图13。
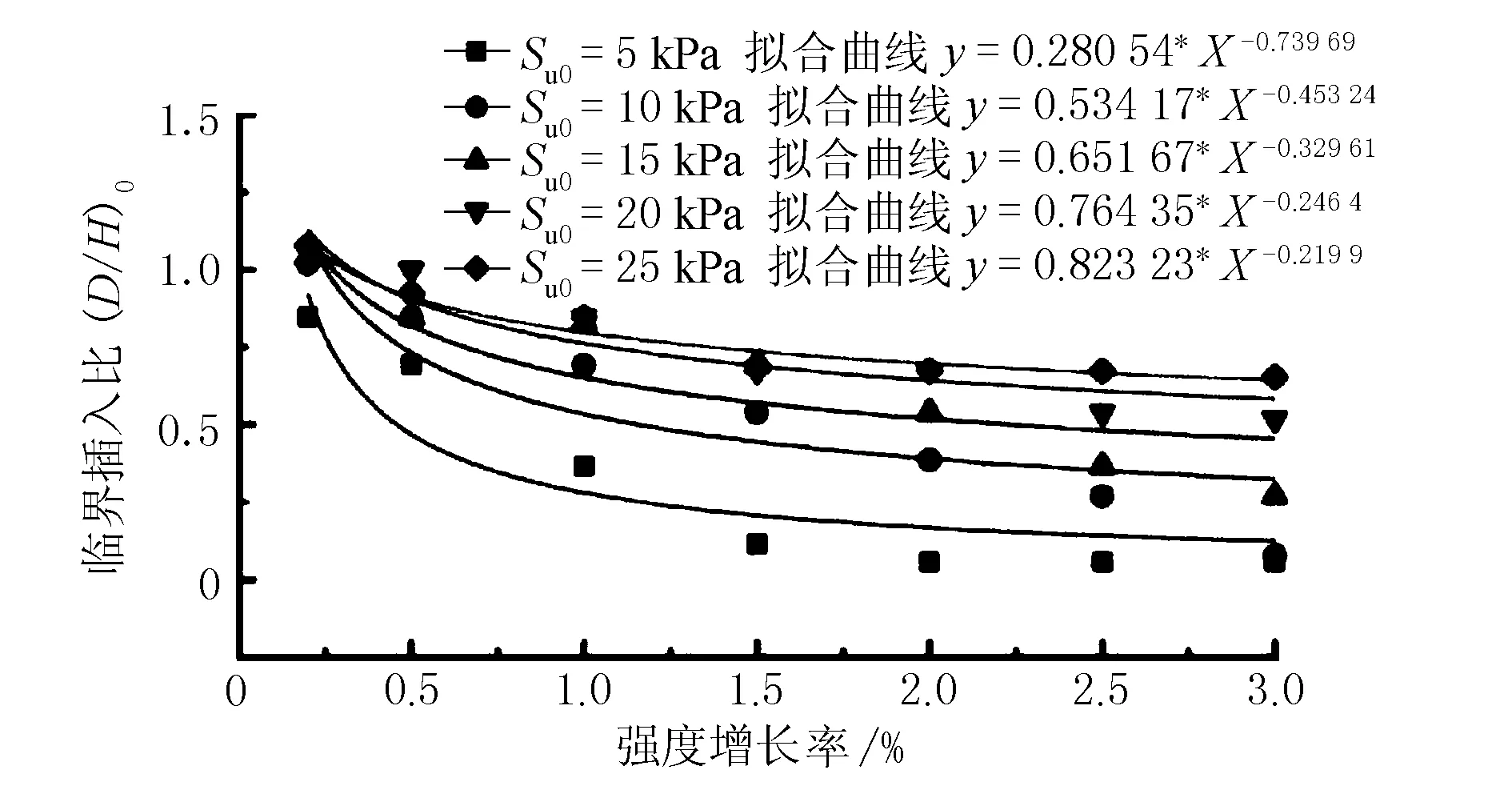
图13 H=26 m时拟合曲线
H=26 m时,拟合曲线的残差平方和(SSE)和R2(COD)的计算结果见表6,其中残差平方和趋近于0,R2仍大于0.8。表明H=26 m时的5条拟合曲线拟合结果较好。

表6 H=26 m时拟合方程评价参数计算结果
对部分实测值大于预测值的点位,其所处曲线和具体数值(取3位有效小数)见表7。

表7 实测值大于预测值点位的数值分析
由表7可知,当土体初始强度为5,10,15 kPa时,虽临界插入比的实测值和预测值相差较小,但由于此时实测值和预测值均已小于1,故差值与预测值的比值反而较大。故在实际基坑工程中,出于偏安全的考虑,建议当土体初始强度为5 kPa时,取1.5的安全系数;当土体初始强度为10,15 kPa,安全系数取为1.3;当土体初始强度为20,25 kPa可取1.15的安全系数;实际工程中,使用对应的安全系数将预测值放大后使用。
4 结语
由使用基于winkler地基模型的两阶段法分析求解临近桩基因基坑开挖所产生的位移时,需知道临近桩基的边界条件这一前置条件,因此对基坑开挖滑动破坏面开展分析。并由此得出以下结论。
1) 传统圆弧滑动法中,土体滑动面始终通过支护结构嵌固端底部这一假设并不合理。土体滑动面应随着支护结构插入比的增大而逐渐上移,经过支护结构嵌固端底部,并最终经过围护经过嵌固部分。可将土体滑动面恰好经过支护结构嵌固端底部时对应的支护结构嵌入深度称为临界嵌深,此时的插入比为临界插入比(D/H)0。
2) 对软土层,其土体强度随深度变化,满足Su=Su0+λz。当土体增强率λ相同时,土体初始不排水抗剪强度Su0越小,土体深度每向下增加时,每米土体的强度增长百分比逐渐减小,可等效为坚硬土层埋深变浅,滑动面通过围护结构底端所需的临界插入比减小。同样,当基土体初始不排水抗剪强度Su0相同时,土体增长率增大会导致土体强度随深度增加而快速增大,也可等效为坚硬土层可等效为坚硬土层埋深变浅,滑动面通过围护结构底端所需的临界插入比减小。
3) 当已知基坑开挖深度H时,可以使用土体初始不排水抗剪强度Su和土体强度增长率判断此基坑发生坑底隆起时滑动面和围护结构的关系。若围护结构插入比大于临界插入比,即D/H≥(D/H)0,基坑土体滑动破坏面通过支护结构嵌固端,出于偏安全考虑,计算基坑开挖安全系数和对坑外桩基的影响时,可认为坑外土体滑动破坏面恰好经过围护结构底部,取基坑底部至支护结构底部的距离为滑动面滑动半径。反之,当D/H<(D/H)0时,土体滑动破坏面位于围护结构以下的土体内,不经过围护结构,此时滑动半径需另行确定。
4) 对使用LimitState GEO软件得出的不同开挖深度、土体强度增长率和土体强度下的临界插入比数据进行拟合,得出对应的拟合曲线,其基本表达式为:y[(D/H)0]=a·xb。可以此根据土体强度增长率得出对应的临界插入比预测值。
5) 出于偏安全考虑,对有限元分析所得数据,预测值小于实测值的数据进行分析修正,并以此给出了安全系数。当开挖深度大于25 m,软土初始强度为5,10,15 kPa时,取安全系数为1.5;当开挖深度大于25 m,土体初始强度为10,15 kPa,取安全系数为1.3;其余情况取安全系数为1.1。实际工程中,使用对应的安全系数将预测值放大后使用。

