Construction of a Class of Gerstenhaber Algebras
,
(School of Mathematics and Statistics, Henan University, Kaifeng 475004, China)
Abstract: For any K-algebra A, based on Hochschild complex and Hochschild cohomology of A, we construct a new Gerstenhaber algebra, and give Gerstenhaber algebra epimorphism from the new Gerstenhaber algebra to the Gerstenhaber algebra of the Hochschild cohomology of A.
Keywords: Gerstenhaber algebra;Hochschild cohomology;Differential graded Lie algebra
§1.Introduction
In the past decades, Hochschild cohomology theory is becoming indispensable in many branches of algebra, such as representation theory, deformation theory, operad theory, and so on [8].Gerstenhaber algebras arose explicitly in M.Gerstenhaber’s work on the Hochschild cohomology theory for associative algebras[7].It plays a very important role in many fields,such as theoretic physics, Poisson geometry, and string topology [9, 12, 13, 16].LetMbe a manifold,V(M) be the algebra of polyvector fields onM, thenV(M) is a Gerstenhaber algebra under the wedge product and the Schouten-Nijenhuis bracket [2].For an associative algebraA, we denote the direct sum of all Hochschild cohomology groups ofAby H∗(A,A).Then H∗(A,A) is a Gerstenhaber algebra under the cup product and the Gerstenhaber bracket [7].But in general,it is very difficult to give the structure of Gerstenhaber algebra on the Hochschild cohomology of an associative algebra.For some special algebra classes, the Gerstenhaber algebraic structure on Hochschild cohomology is given (see [1, 6, 10, 11, 15]).
This note is dedicated to studying the construction of Gerstenhaber algebras.In[4]and[14],the authors proved that there is a Gerstenhaber algebra structure on Hochschild cohomology of a Hom-associative algebra and singular Hochschild cohomology of an associative algebra respectively.Recently,when considering the multiplicative compatibility,Das gives a construction of Gerstenhaber algebra by using the nonsymmetric operad [5].Here, for any associative algebraA, from the Gerstenhaber algebra H∗(A,A), we construct a new chain complex and prove that there is a Gerstenhaber algebraic structure on the cohomology of this new chain complex.Therefore, we give a method to construct a class of new Gerstenhaber algebras.Moreover, we also give an epimorphism from the new Gerstenhaber algebra to the Gerstenhaber algebra ofA.
§2.Hochschild cohomology of associative algebras
In this section, we recall the Gerstenhaber algebraic structure on Hochschild cohomology of an associative algebra.
For the details see [7].Let K be a field,Abe an associative K-algebra andMbe a bimodule overA.Denote byC0(A,M)=MandCn(A,M)=Hom(⊗nA,M).Recall that the Hochschild cochain complex of associative algebraAwith coefficients bimoduleMis the cochain complex(Cn(A,M),δn)n≥0, where the coboundary operatorsδ0:C0(A,M)→C1(A,M),m■→[-,m],[a,m]=am-mafor anya∈A, and forn≥1,δn:Cn(A,M)→Cn+1(A,M) is given by
for allf ∈Cn(A,M),a1,a2,···,an+1∈A.Thenn-th Hochschild cohomology group ofAwith coefficientsMis defined by
whereZn(A,M)=Kerδnis the space ofn-cocycles andBn(A,M)=Imδn-1the space ofncoboundaries.
We take bimoduleMby the regularA-bimoduleA.There are not only Lie algebra structure,but also associative algebraic structure on⊕i≥0Ci(A,A) and⊕i≥0Hi(A,A).There is a graded Lie algebraic structure on⊕i≥0Ci(A,A) by setting
where
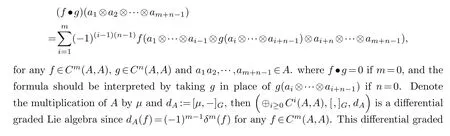
(i) (A,∗)is an associative algebra and it is graded commutative;
(ii) (⊕i≥1Ai,[,])is a graded Lie algebra,where the degree of[,]is-1;
(iii)satisfies the graded Leibniz rule: [α∗β,γ]=[α,γ]∗β+(-1)|α|(|γ|-1)α∗[β,γ],where|α|is the degree of homogeneous element α.
LetAandBbe two Gerstenhaber algebras.Ahomomorphism of Gerstenhaber algebras φ:A→Bis a homomorphism of graded commutative associative algebras and a homomorphism of graded Lie algebras with degree-1 brackets.In 1963, Gerstenhaber proved the Hochschild cohomology groups of an associative algebra have a Gerstenhaber algebraic structure.
§3.A new Gerstenhaber algebra

Proposition 3.1.With the above notations.The pair(¯g,〚,〛)is a graded Lie algebra,and the mapΘ:¯g→g,

for any(f1,f2,···,fm)∈Zm(A,A),where˜dA=〚(µ,µ),-〛G.
Proof.First, for any (f1,f2,···,fm)∈Bm(A,A), that is, there exists an element (h1,h2,···,hm-1) in ˜Cm-1(A,A) such that (f1,f2,···,fm)=∂m-1(h1,h2,···,hm-1), we getf1+f2+···+fm ∈Cm(A,A) and
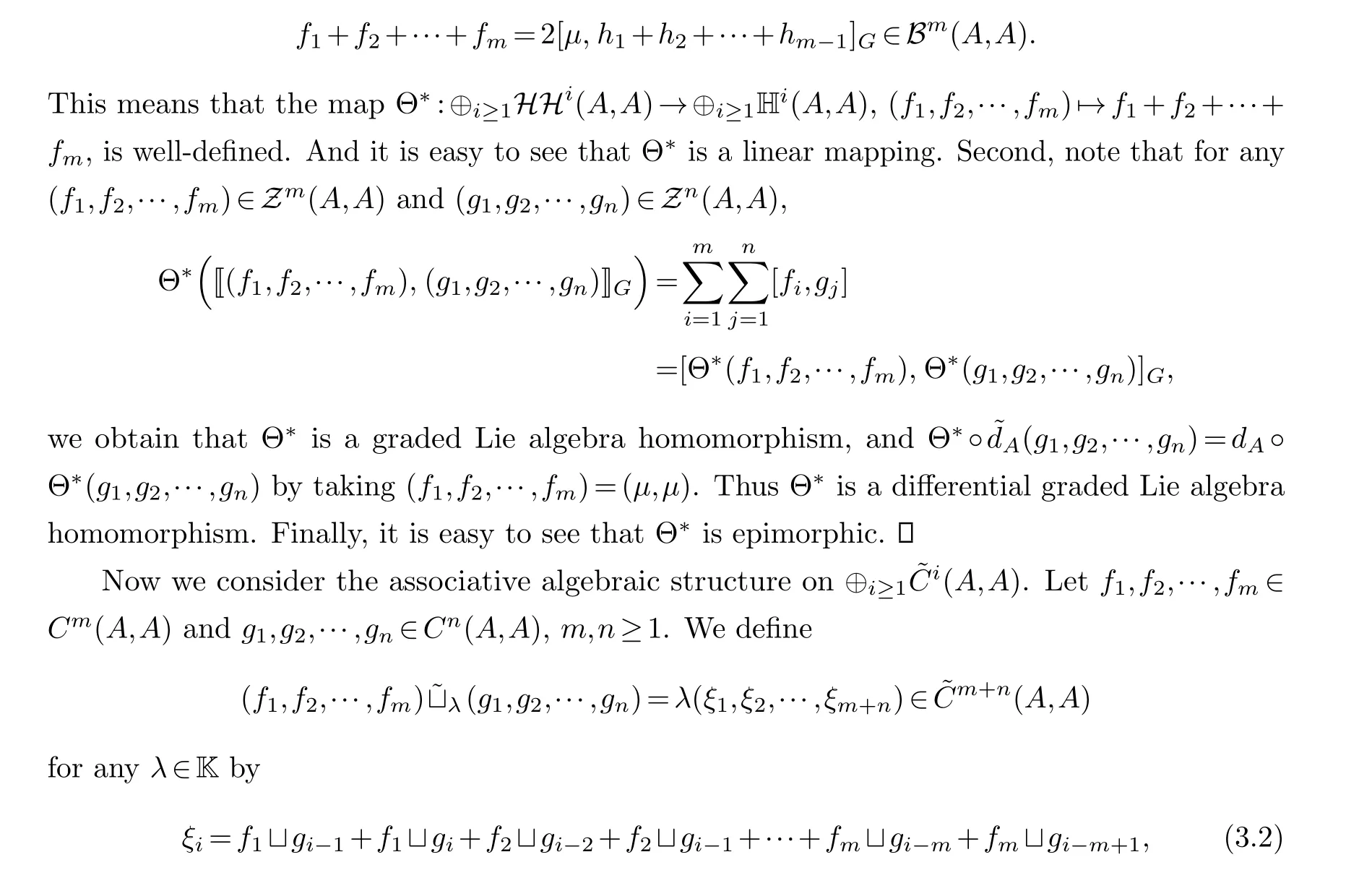
wherefi=0 ifi/∈{1,2,···,m}andgj=0 ifj/∈{1,2,···,n}.Note thatξican be expressed as
and⊔is associative, one can check that the associative law of the product ˜⊔λholds.
Proposition 3.5.For any f1,f2,···,fm ∈Cm(A,A),g1,g2,···,gn ∈Cn(A,A)and h1,h2,···,hp ∈Cp(A,A),m,n,p≥0,we have
Moreover, the differential∂nis a graded derivation for the product ˜⊔λ.
Proposition 3.6.For any f1,f2,···,fm ∈Cm(A,A)and g1,g2,···,gn ∈Cn(A,A),m,n≥1,we have
This means that the equation (1.4) holds for allm,n≥1.

Proof.Here, we only need to show that Θ∗is a graded associative algebra homomorphism.
For any(f1,f2,···,fm)∈Zm(A,A),(g1,g2,···,gn)∈Zn(A,A),m,n≥1,by direct calculation,we have

 Chinese Quarterly Journal of Mathematics2023年4期
Chinese Quarterly Journal of Mathematics2023年4期
- Chinese Quarterly Journal of Mathematics的其它文章
- Exact Boundary Controllability for a 1-D Second-Order Quasilinear Hyperbolic System
- Singularity of Two Kinds of Four Cycle Graphs
- Initial Boundary Value Problem for Pseudo-Parabolic p-Laplacian Type Equation with Logarithmic Nonlinearity
- Subordination and Superordination Results for a Certain of Integral Operator Involving Generalized Mittag-Leffler Functions
- Competitive Equilibrium of Central Bank Digital Currency and Private Cryptocurrency: A Perspective of Regulatory
- Space-Time Legendre Spectral Collocation Methods for Korteweg-De Vries Equation
