Initial Boundary Value Problem for Pseudo-Parabolic p-Laplacian Type Equation with Logarithmic Nonlinearity
-,-
(College of Mathematics and Information, South China Agricultural University,Guangzhou 510642, China)
Abstract: In this paper, we study the initial boundary value problem of pseudo-parabolic p-Laplacian type equation, which be use to model some important physical and biological phenomena.By using the potential well method,we obtain the global existence,asymptotic behavior and blow up results of weak solution with subcritical initial energy.Then we also extend these results to the critical initial energy.
Keywords: Pseudo-parabolic equation; p-Laplacian; Logarithmic nonlinearity
§1.Introduction
In this paper, we consider the initial boundary value problem of pesudo-parabolic equation with logarithmic nonlinearity:
Here,u0∈W1,p0(Ω) and Ω is a bounded domain in Rnwith smooth boundary∂Ω.The constant coefficientsa,bare positive, andpsatisfies
The pseudo-parabolic equationut-a∆ut-∆u=f(u) can be used to model a series of physical and biological phenomena, such as the seepage of homogeneous fluid, nonlinear dispersive,long waves and the aggregation of population [1–3,15,20].Furthemore, the equation also plays an important role in analysis of nonstationary processes in semiconductors in the presence of sources [10,11], where ∆ut-utstands for the free electron density rate, ∆ustands for the linear dissipation for free change current, andf(u) stands for the source of free electron current.In addition, affected by multiple factors, such as atoms, ions, etc.,-∆uin the pseudo-parabolic equation is usually replaced by∇(|∇u|p-2∇u).
Many authors have studied problems similar to (1.1), such as the problem
In [5], Cao et al.considered the Cauchy problem of (1.3) withf(u)=uq.Using the contraction mapping principle, they got the solution that would blow up in finite time.Xu et al.[22]investigated the excitence and asymptotic behavior of the global solution for initial boundary value problem.ForWang et al.[21] investigated the existence,decay estimate of the global solutions and global nonexistence of solutions with subcritical and critical initial energyJ(u0)≤d, and proved the blow-up results with supercritical initial energy,which are extended to fractional semilinear pseudo-parabolic equation by Li et al.[13].
Logarithmic nonlinear sources are widely used in inflationary cosmology and supersymmetric field theory, quantum mechanics and physics, such as supersymmetric fracture models.In [6],Chen et al.studied the initial boundary value problem with logarithmic nonlinear term.Cao et al.in [4] considered the following initial boundary value problem withp=q
and obtained the global existence of weak solution.For the case ofp/=q, Ding et al.proved that weak solution existed all time forI(u0)>0.Besides, they also proved that the weak solution will blow up at infinite time with 1 For problem Sun et al.[19] studied the initial boundary value problem for problem (1.5), and obtain the blow up result.Li et al.[12] considered such pseudo-parabolic equation with variable exponents, and got the existence and blow up result of weak solution.In [23], Zeng et al.obtained the existence and non-existence of such equation with logarithmic nonlinear term. Inspired by the above works, through potential well method, we study the existence and blow up of solutions for the problem (1.1).In recent years, the potential well method has been widely used in various mathematical physics problems.This method was originally proposed by Sattinger in [18].Then the further research was carried out on it by Payne and Sattinger in [16].The potential well method was generalized to the semilinear hyperbolic equations and parabolic equations by Liu et al.in [14].In this paper, we mainly discuss the following two cases: subcritical initial energyJ(u0) The main results of this paper are the following theorems. Theorem 1.1.Assumed that p satisfy(1.2)and u0∈W1,p0(Ω).If u0∈W,then the problem(1.1)admits a global weak solution and exist a constant α1>0and t>0such that If u0∈V,then the weak solution u(t)of problem(1.1)blows up in finite time(the definition of W and V are given below). Theorem 1.2.Assumed that p satisfy(1.2),u0∈W1,p0(Ω)and J(u0)=d.If I(u0)≥0,then the problem(1.1)admits a global weak solution.If I(u0)>0,there exist t1>0adn α2>0such that If I(u0)<0,then the weak solution u(t)of problem(1.1)blows up in finite time. Lemma 2.2.([9])For some constants θ>0,any t>0and0 Now, we give the proof of Theorem 1.1 by potential well method. Proof of Theorem 1.1.Assume{ωj(x)}are the eigenfunctions of the Laplacian operator,normalized by‖ωj‖2=1.Without loss of generality,{ωj(x)}forms a basis ofW1,p0(Ω).We build approximate solutionsum(x,t) to the problem (1.1): And, by a direct calculation, we know Letm→∞in (3.1), we get Moreover, by (3.2), we obtainu(x,0)=u0(x).Therefore, we prove that the existence of weak solution is global.Next we consider asymptotic behavior for weak solution. Settingφ=uin (2.4), we have Obviously, through the young inequality, we deduce Combining with (3.12), by using Gronwall inequality, for anyt>0, there holds Next, we will proof the blow-up result.According to Lemma 2.3, we haveu∈Vfor allt∈[0,∞).We define a function as Therefore, we have According to the Lemma 2.4, we haveI(λ∗u)=0.Then, by (2.3) and the definition of depth of potential welld, we get which leads to Therefore, by lemma 2.2, there exists aT>0 such that which is a contradiction withT=+∞. Now, we generalize the above results to critical initial conditionJ(u0)=d. Then the remainder of the proof is similar to Theorem 1.1. Next, we claim thatu∈Wfort>t1.In fact, if false, there existt0>0 that is the first time such thatI(u(t0))=0.Then, by the definition ofd, we haveJ(u(t0))≥d.Combine with (2.5) Hence, we deduceJ(u(t0))=d, which implies that isut ≡0 for 0≤t≤t0, which contradicts withI(u0)>0.Therefore,u∈Wfort1 Now, we study the asymptotic behavior of problem (1.1) with initial timet1, then we can getI(u(t1))>0 and According to the continuity ofI(u) andJ(u) about timet, there exists a sufficiently smallt0>0 such thatI(u(t0))<0 andJ(u(t0))>0.Combining (3.9), we haveut/=0 for 0 From Lemma 2.3 and takingt=t0as the initial time, we haveu(x,t)∈Vfort>t0. Then the remainder of the proof is the same as Theorem 1.1.§2.Preliminary


§3.The proof of main results


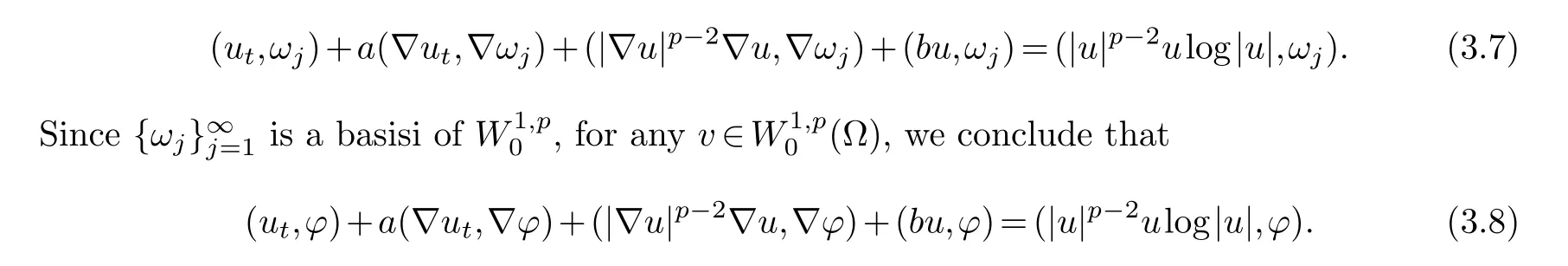
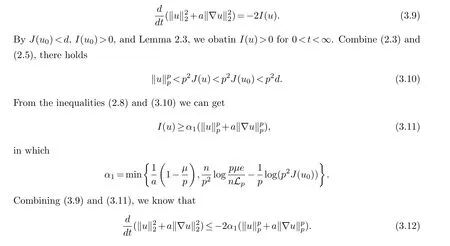
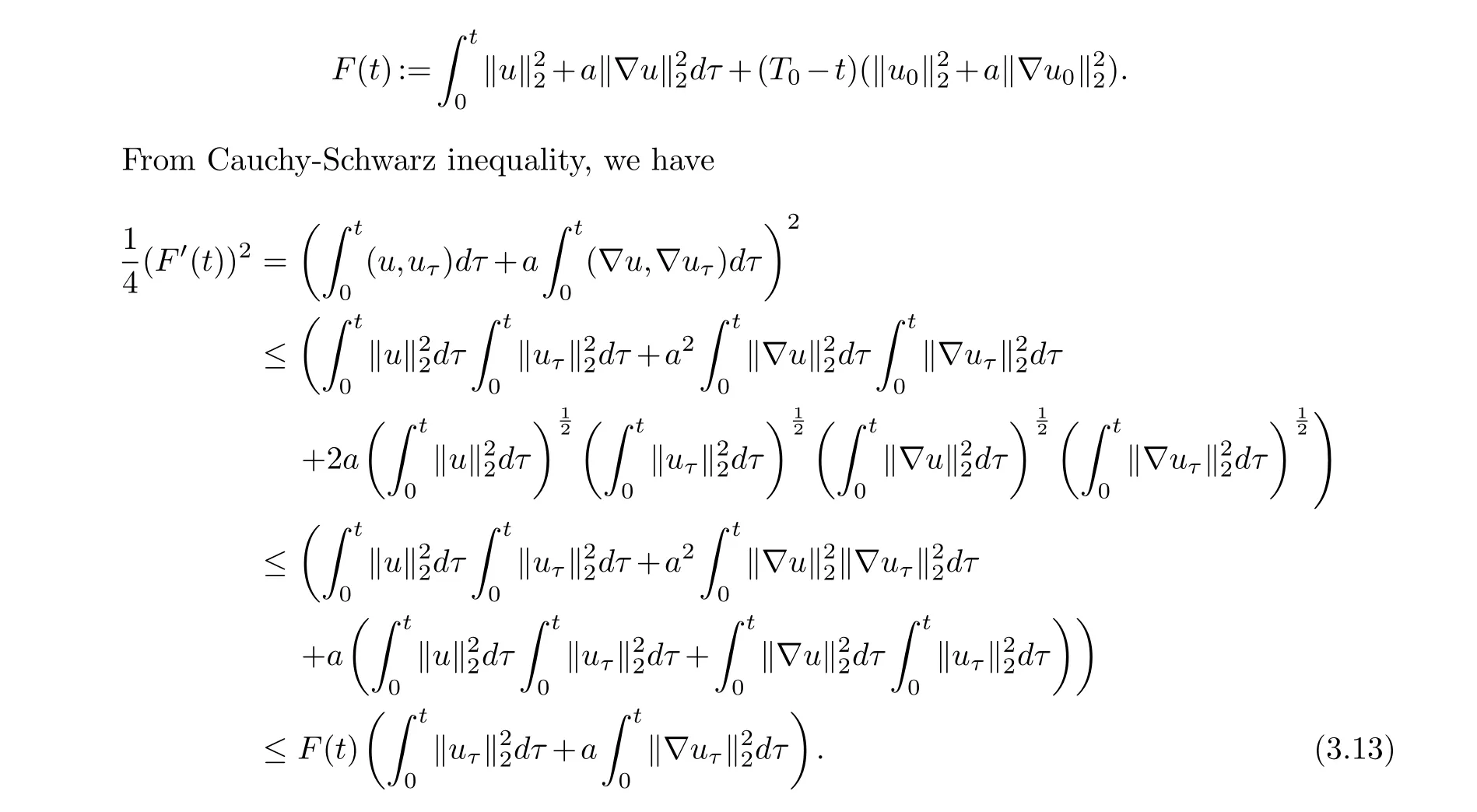

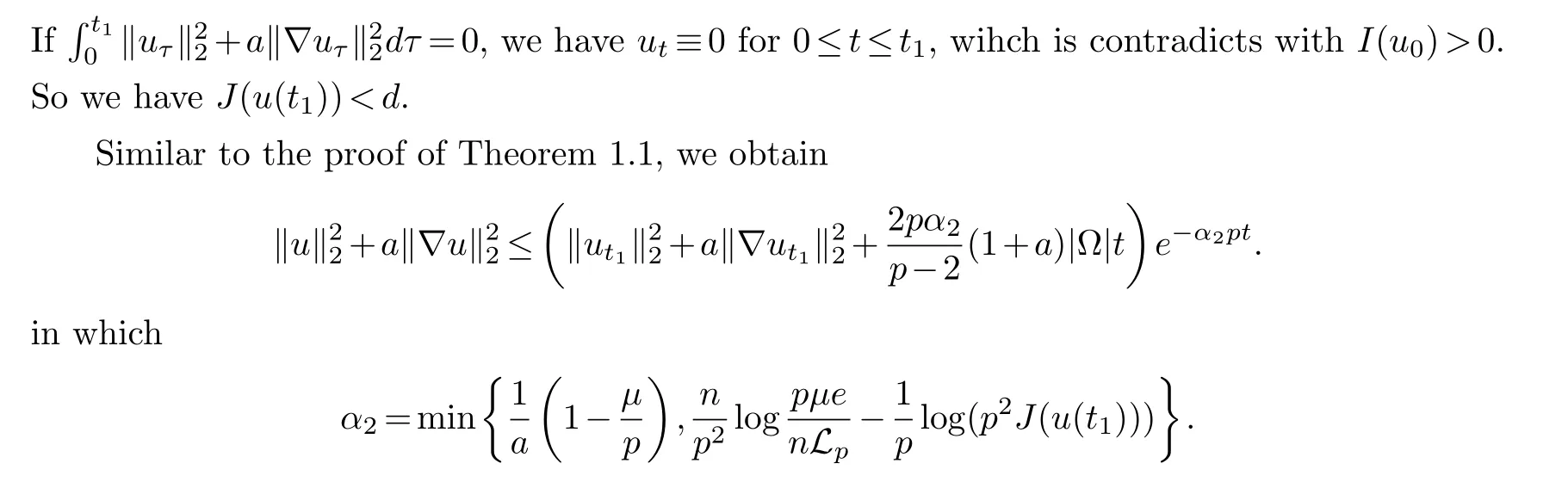
 Chinese Quarterly Journal of Mathematics2023年4期
Chinese Quarterly Journal of Mathematics2023年4期
