1 μm 波段高功率超辐射发光二极管

伏丁阳， 高 欣， 赵仁泽， 张 悦， 苏 鹏， 薄报学

（长春理工大学 高功率半导体激光国家重点实验室， 吉林 长春 130022）

1 引 言

超辐射发光二极管（Superluminescent diodes，SLD）作为一种高功率、宽光谱发射的光源，具有相干长度短和远场发散角小等优点，广泛应用于波分复用（Wavelength division multiplexing，WDM）、光时域反射仪（Optical time domain reflectometer，OTDR）以及光纤陀螺仪（Fiber-optic gyroscope，FOG）等领域。同时，水汽对1.06 μm 的吸收较低，并且水在1 μm 附近存在零色散的情况，因此1 μm 波段的SLD 可以在含水分气氛条件下测量目标，根据光谱中各频率的干涉信号来获得深度相关的信息，使其方便用于医学诊断领域中的光学相干层析成像（Optical coherence tomography，OCT）[1-2]。目前，1 μm 波段OCT 系统光源的光谱半宽应不低于75 nm。对SLD 的需求正在朝着高输出功率和宽光谱半宽的目标迈进。SLD 的高功率输出特性，既可以实现在光纤中更长距离的信息传输、降低噪声对测量结果的影响，又可以提高FOG 系统的精度和灵敏度，也可以提升OCT系统的成像速率，还可以增加OTDR 系统的动态范围与测量距离。而SLD 宽光谱特性则可以实现OCT 系统轴向分辨率的提高。

自从1971 年Kurbatov 等[3]首次制备出SLD 之后，如何提高SLD 的输出性能成为研究热点。Ohgoh 等[4]制备了中心波长为1.05 μm 的倾斜波导结构的InGaAs/GaAs 非对称双量子阱结构SLD，获得了33.4 mW 的连续波输出功率和77.5 nm 光谱半宽。2015 年，段利华等[5]制备了中心波长为1 053 nm 的弯曲波导吸收区结构的InGaAs/GaAs 双量子阱SLD，在100 mA 注入电流下，SLD模块尾纤输出功率达到2.5 mW，相应的光谱半宽为24 nm。2018 年，Kwon 等[6]制备出中心波长1.08 μm 的InGaAs/GaAs 非对称双量子阱结构的SLD，在250 mA 注入电流下获得20 mW 的输出功率和122 nm 的光谱半宽。由于J 型波导后端面的反射作用使得这种结构的SLD 可以实现更高的输出功率，Kafar 等[7]制备了J 型波导结构的蓝紫色SLD，在450 mA 注入电流下获得了大于200 mW的输出功率。可以看出，现阶段1 μm 波段SLD 的输出功率还有待提高。

为了改善1 μm 波段SLD 的输出特性，本文设计了非均匀阱宽大阱深的三量子阱结构作为有源区以提高增益、改善谱宽、减小高注入下的载流子泄露并通过缩小波导层和限制层AlGaAs 材料中Al 组分的差值，降低器件的远场发散角，改善器件光束特性。另外，采用时域有限差分法结合光束传输法仿真模拟了J 形波导不同结构参数与损耗系数之间的关系。基于仿真结果，确定器件结构参数，并对制备工艺进行了优化。

2 器件设计

J 型波导结构的SLD 结构示意图如图1 所示，芯片前腔面镀制增透膜，后腔面镀制高反膜。弯曲波导腔面作为输出腔面配合前腔面镀制的增透膜可以使光在纵向上的振荡得到有效抑制，只有极少部分光反射回波导内，从而达到抑制F-P 振荡的目的，使器件稳定工作在超辐射状态，抑制激射引起的光谱变窄。后腔面的高反膜设计提供了波导内的双程增益，有效增加腔内的光增益长度，有利于器件输出功率的提高。

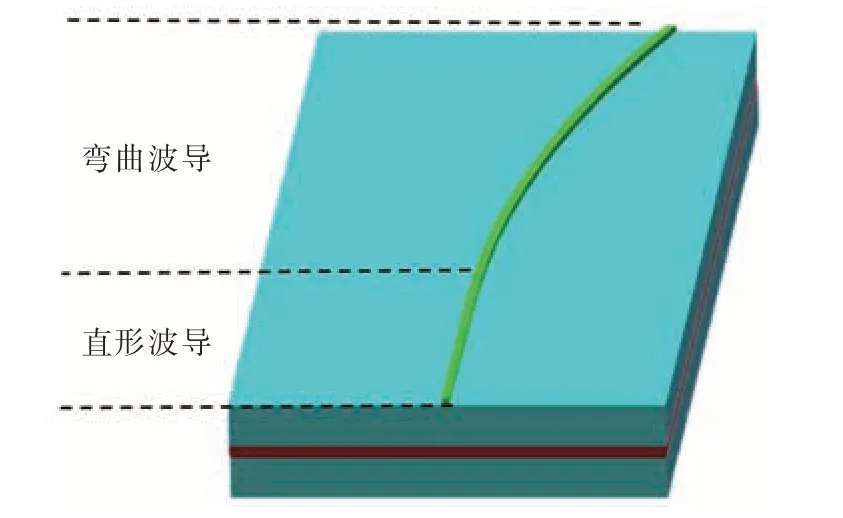
图1 J 型波导结构SLD 示意图Fig.1 Schematic diagram of J-shaped waveguide structure SLD

波导弯曲会不可避免地产生辐射损耗。如果损耗过大，可能导致器件输出功率较低或器件发热严重而无法正常工作。对弯曲损耗进行定量分析意义重大。损耗系数α由下列公式联立给出：

其中，A代表振幅，I是输出功率，I0是输入功率，L是波导长度。

在器件设计过程中，首先仿真了不同刻蚀深度对脊形波导基模模场尺寸的影响，并采用光束传输法仿真了不同波导结构参数（刻蚀深度、脊宽、曲率半径）情况下，光在波导中的传输情况，得到了不同波导结构参数对损耗系数的影响。

仿真过程采用的器件的外延结构参数如表1所示。采用相同In 组分不同阱宽的三量子阱结构作为有源区达到扩展器件光谱半峰宽的目的。此外，考虑到单量子阱对非平衡载流子的收集能力较弱[8]，本文利用GaAsP 替代传统的GaAs 作为垒层材料增大阱深并结合多量子阱结构以获得高增益和高注入下的低载流子泄露，提高载流子的注入效率。其次，电导率大、热阻小的AlGaAs 被作为波导层与限制层材料。研究了波导层和限制层AlxGa1-xAs 材料中Al 组分的差值Δx对远场发散角的影响，如图2 所示。结果表明，Δx=0.1 时的垂直远场发散角较Δx=0.3 时下降了6.5°，即缩小波导与限制层材料中Al 组分的差值有利于降低基模光限制因子，进而达到降低器件远场发散角以改善光束特性的目的。

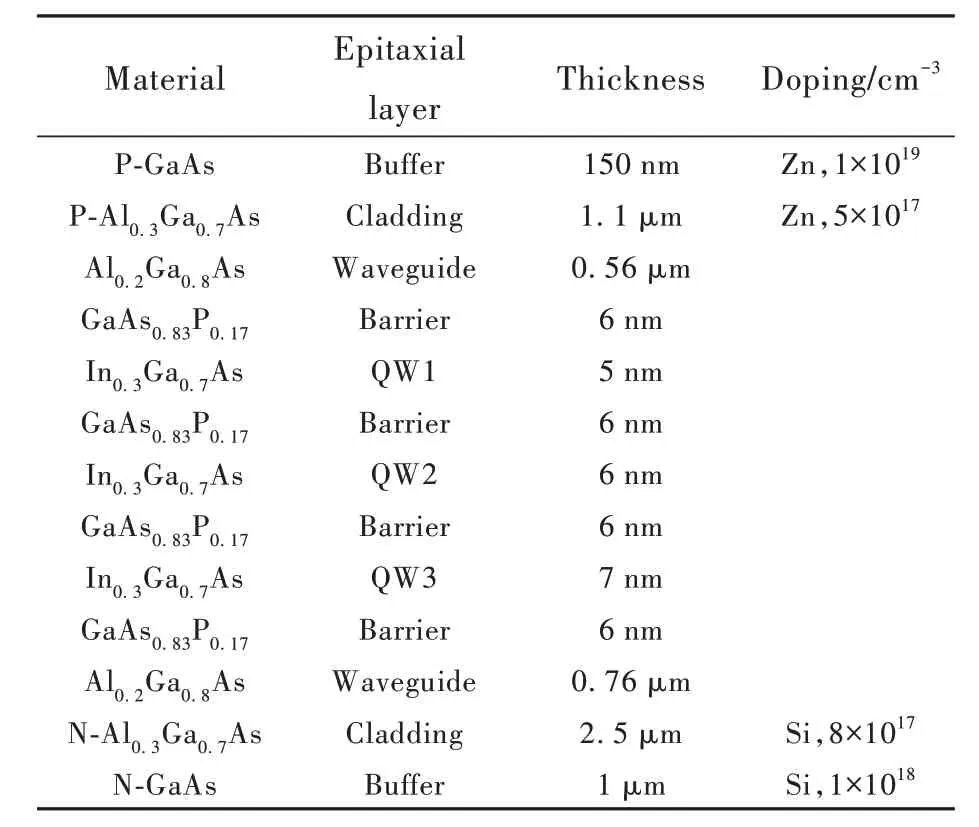
表1 器件外延结构参数Tab.1 Device epitaxial structure parameters

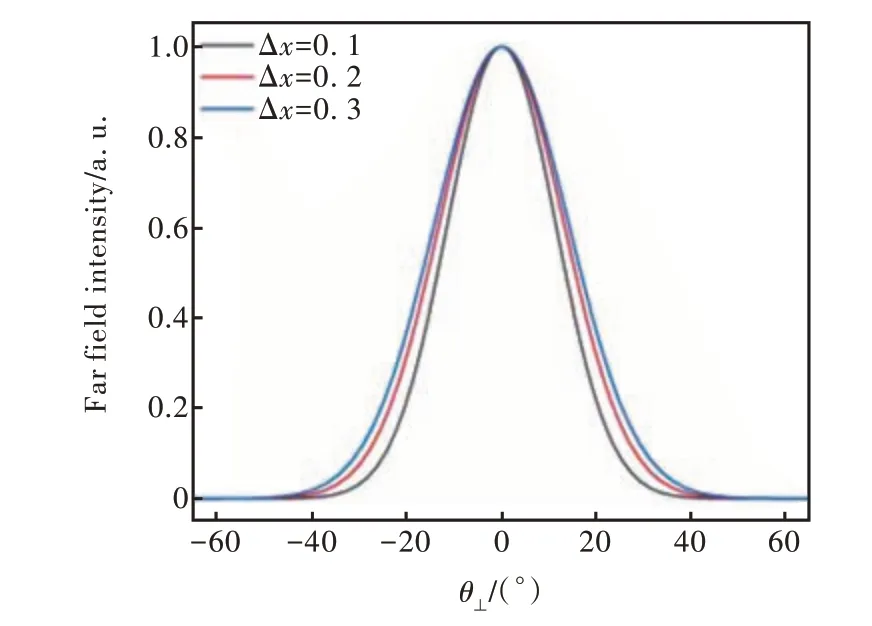
图2 归一化的垂直远场发散角随波导层和限制层Al 组分差值Δx 的变化趋势Fig.2 The trend of normalized vertical far-field divergence angle as a function of the difference in Al composition Δx between the waveguide layer and the limiting layer

本文首先进行模型建立，将如图1 所示的单管划分为脊波导区域和脊波导两侧被刻蚀区域。其等效图形如图3 所示。脊波导两侧被刻蚀区域的外延结构相同且刻蚀深度也相同，因此它们的等效折射率相同。设脊型波导两侧被刻蚀区域的等效折射率为n1，脊波导区域的等效折射率为n。

图3 等效图形Fig.3 Equivalent figure

其次，利用Mode Solutions 仿真n1与Δn=n-n1随刻蚀深度的变化情况，如图4（a）、（b）所示。从图中可以看出，刻蚀深度小于1.1 μm 时n1几乎保持不变。当刻蚀深度达到一定值后，n1对刻蚀深度的变化变得很敏感，刻蚀深度的少量增加会导致n1的急剧下降。刻蚀深度大于1.1 μm 时n1开始下降，Δn随着刻蚀深度的增加而增加。这表明随着刻蚀深度的增加，波导对光场的限制能力逐渐增强。

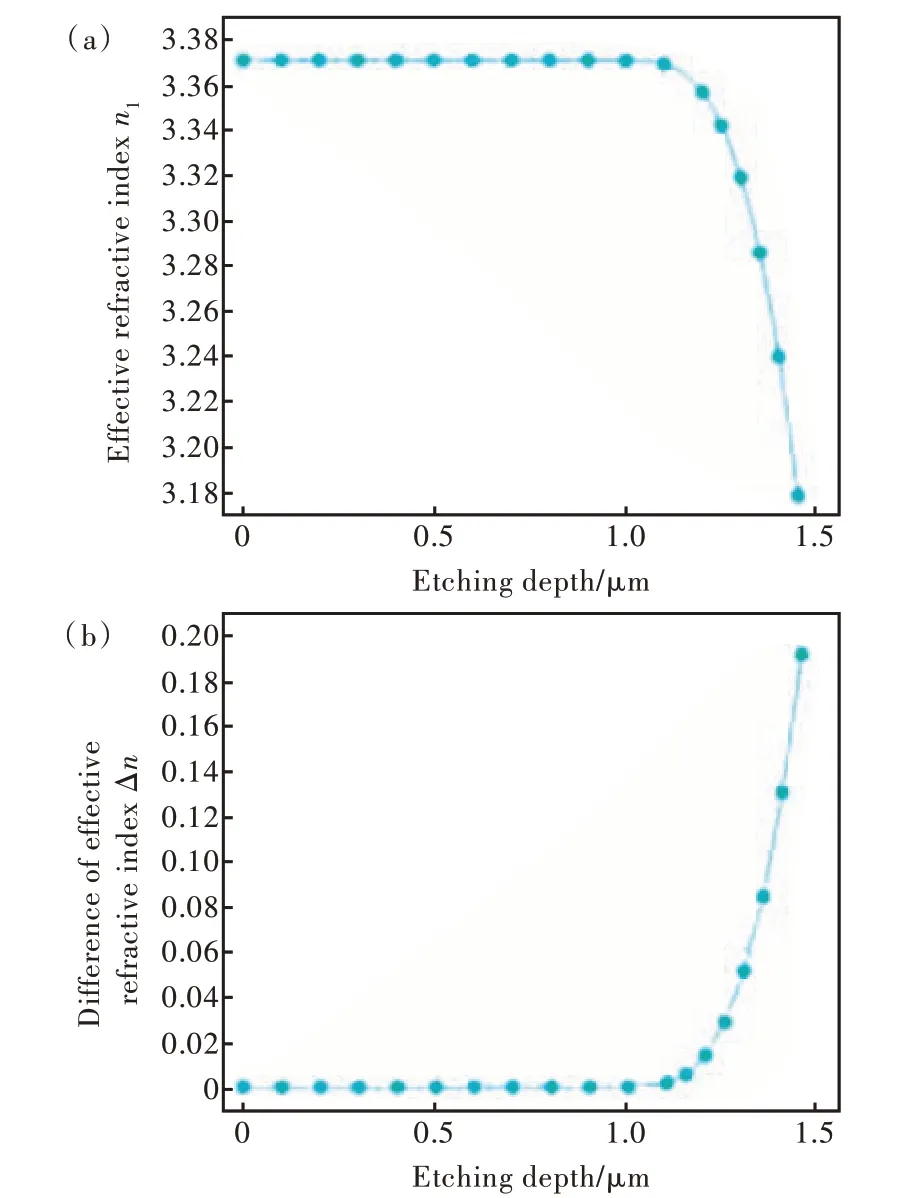
图4 刻蚀深度与n1（a）和Δn（b）之间的关系Fig.4 The relationship between etching depth and n1（a） and Δn（b）

再次，为了初步确定刻蚀深度，本文仿真了基模模场尺寸随刻蚀深度H的变化趋势，如图5 所示。仿真采用的脊波导宽度为3 μm。从图中可以看出，随着刻蚀深度的增加，分布在±1.5 μm 范围外的光场强度随之下降。这表明基模模场的分布范围逐渐收缩到脊波导中，光场的侧向尺寸逐渐减小。当刻蚀深度＜1.1 μm 时，光场模式可扩展到脊型区两侧较大距离，载流子的侧向扩展会导致器件的增益减小[9]。当刻蚀深度＞1.1 μm 时，分布在脊波导外侧的光场强度近似为零。因此，刻蚀深度应该大于1.1 μm。

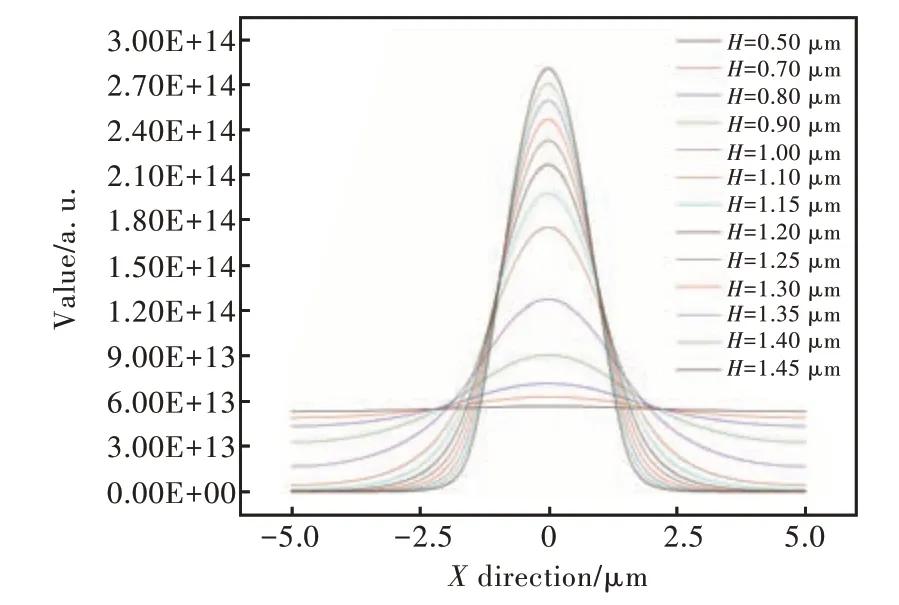
图5 基模模场尺寸随刻蚀深度的变化趋势Fig.5 The variation trend of fundamental mode field size with etching depth

随后，对脊宽为3 μm、曲率半径为13.6 mm的器件在不同刻蚀深度下波导中光场传输情况进行仿真，如图6 所示。从图6（a）可以看出，刻蚀深度为1 μm 时，由于脊波导与脊波导两侧被刻蚀区域等效折射率差较小，光场完全脱离波导限制[10]；图6（b）中输出端面电场振幅为0.331，此时波导损耗较大，可能导致器件输出功率较低；图6（c）中输出端面电场振幅为0.996。刻蚀深度增加导致波导对光场的限制能力增强，波导损耗下降。另外，随着刻蚀深度的增加，分布在弯曲波导外侧的光场减少，这也定性地证明了弯曲波导损耗随着刻蚀深度的增加而降低。

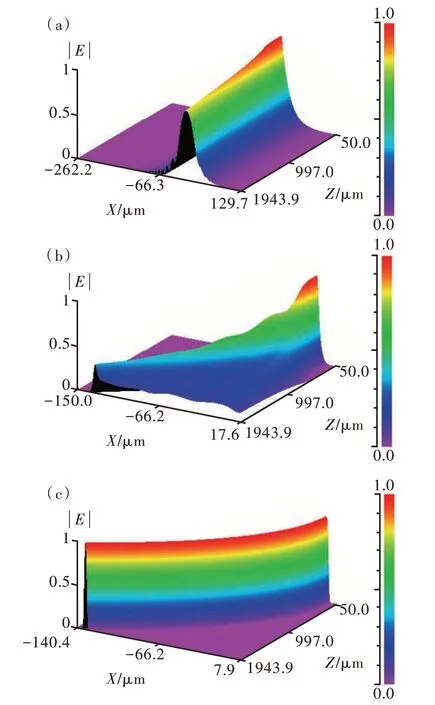
图6 不同刻蚀深度情况下光场传输情况。 （a）1 μm；（b）1.1 μm；（c）1.25 μm。Fig.6 Light field transmission under different etching depths. （a）1 μm. （b）1.1 μm. （c）1.25 μm.

最后，根据以上仿真结果，联立公式（1）、（2），得到损耗系数与刻蚀深度之间的关系并最终确定了刻蚀深度，仿真结果如图7 所示。需要注意的是，由于刻蚀深度为1 μm 及以下时，波导完全丧失对光场的限制能力，因此并没有计算此时的损耗系数。从图中可以看出，损耗系数随着刻蚀深度的增加而减小。当刻蚀深度大于1.15 μm 时，损耗系数变化很小。考虑到波导损耗过低容易导致器件在相对较低的电流下产生较大的光谱调制甚至激射，刻蚀深度被定为1.12 μm。

图7 损耗系数与刻蚀深度之间的关系Fig.7 The relationship between loss coefficient and etching depth

基于以上的仿真结果，我们对刻蚀深度为1.12 μm、曲率半径为13.6 mm 的器件在不同脊宽下波导中光场传输情况进行仿真，如图8 所示。图8（a）中输出端面电场振幅为0.37，此时脊宽较窄，波导对光场的约束较弱[11]。图8（b）中输出端面电场振幅为0.882；图8（c）中输出端面电场振幅为0.958。随着脊宽的增加，分布在弯曲波导外侧的光场随之减少，这定性证明了弯曲波导损耗随着脊宽的增加而降低。

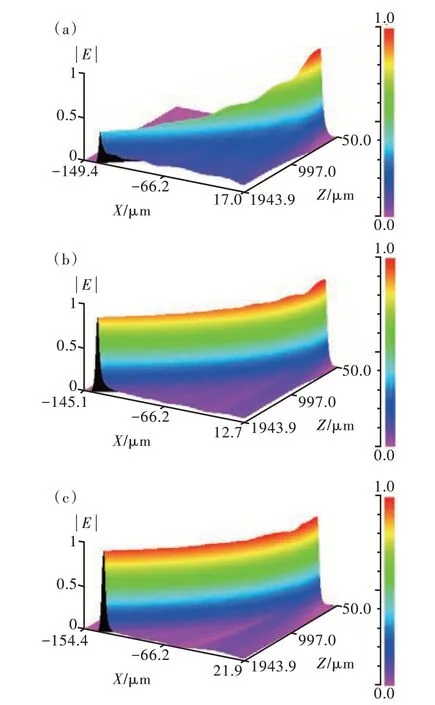
图8 不同脊宽情况下光场传输情况。 （a）1.5 μm；（b）3 μm；（c）4.5 μm。Fig.8 Light field transmission under different ridge widths.（a）1.5 μm. （b）3 μm. （c）4.5 μm.

文中同样得到了损耗系数随波导宽度的变化情况，并确定了器件波导的宽度，结果如图9 所示。图中Δn的不同数值代表不同的刻蚀深度。损耗系数随脊宽的增加而减小。在刻蚀深度相对较浅（Δn=0.003 对应1.12 μm 刻蚀深度）时，脊宽对损耗系数的影响较大；随着刻蚀深度增加（Δn=0.005 时），脊宽对损耗系数的影响减弱。为了尽可能降低波导弯曲损耗并且满足基模条件，最终将脊宽定为3 μm。

图9 损耗系数与脊宽之间的关系Fig.9 The relationship between loss coefficient and ridge width

综上，我们对刻蚀深度为1.12 μm、脊宽为3 μm 的器件在不同曲率半径下波导中光场传输情况进行仿真，如图10 所示。图10（a）中输出端面电场振幅为0.454；图10（b）中输出端面电场振幅为0.753；图10（c）中输出端面电场振幅为0.914；图10（d）中输出端面电场振幅为0.992。随着曲率半径的增加，弯曲波导的曲率减小即弯曲程度减小，分布在弯曲波导外侧的光场随之减少，弯曲波导损耗随之下降。

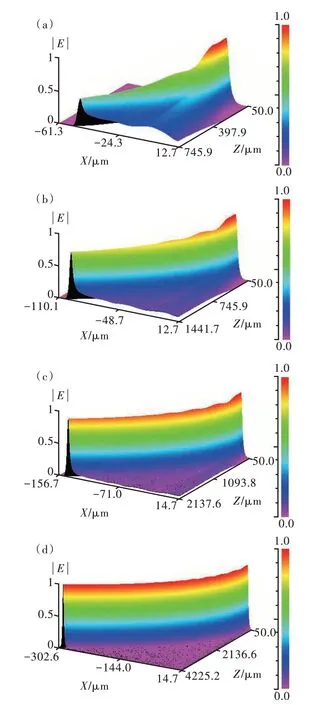
图10 不同曲率半径情况下光场传输情况。 （a）5 mm；（b）10 mm；（c）15 mm；（d）30 mm。Fig.10 Light field transmission under different curvature radii.（a）5 mm. （b）10 mm. （c）15 mm. （d）30 mm.

对仿真结果进行处理，可以得到损耗系数随曲率半径的变化趋势，如图11 所示。

图11 损耗系数与曲率半径之间的关系Fig11 The relationship between loss coefficient and curvature radii

不同曲率半径下的损耗系数对刻蚀深度有较大的依赖性。当曲率半径R＜20 mm 时，浅刻蚀（Δn=0.003）时的损耗系数与深刻蚀（Δn=0.005）时相差较大。损耗系数随刻蚀深度的增加而降低。当R＞20 mm 时，不同刻蚀深度的情况下损耗系数趋于一致。最终制备了曲率半径分别为13.6 mm 和21.8 mm 的两种器件。

除此之外，考虑到器件热阻变化受芯片宽度和长度影响较大，可以达到两个数量级[12]，芯片尺寸被设计为1 994 μm×971 μm，以提高芯片散热能力。

3 器件制备及性能测试

基于仿真结果确定SLD 波导结构参数，并对电极窗口制备工艺以及单层氧化铪增透膜的成膜条件进行优化。最终制备出不同曲率半径的器件，并对其输出特性进行了测试分析。

3.1 器件制备

考虑到脊宽（3 μm）较窄，采用套刻工艺结合BOE 腐蚀SiO2的方法制备电极窗口时可能产生较大的套刻误差，严重影响器件的成品率。因此，我们选择利用Lift-Off 工艺制备电极窗口。在镀制绝缘介质膜时，我们选择磁控溅射设备而不是等离子体增强化学气相沉积（Plasma enhanced chemical vapor deposition，PECVD）。这是由于PECVD 腔室温度相对较高，易导致光刻胶碳化，影响器件制备。另外，磁控溅射设备中等离子体的方向性相对较差。如果用于掩膜的负性光刻胶形貌为“倒梯形”，将会导致SiO2直接镀制在脊波导上方的外延材料上，无法通过Lift-Off 工艺去除。因此通过优化光刻、显影条件，最终获得了形貌相对“陡直”的光刻胶掩膜。Lift-Off 工艺制备电极窗口的结果如图12 所示，可以看出剥离效果较好，脊上无SiO2残留。

图12 Lift-Off 工艺制备电极窗口。 （a）直波导区；（b）弯曲波导区。Fig.12 Effect diagram of electrode window prepared by Lift-Off process. （a）Straight waveguide region．（b）Curved waveguide region.

器件制备工艺流程如下：（1）脊波导图形光刻；（2）ICP 刻蚀，制备出脊宽为3 μm、刻蚀深度为1.12 μm 的J 型波导；（3）利用磁控溅射镀膜机制备SiO2绝缘层；（4）采用Lift-Off 工艺制备电极窗口；（5）磁控溅射制备Ti/Pt/Au 作为P 面电极；（6）N 面减薄抛光；（7）磁控溅射制备Ni/AuGe/Ni/Au作为N 面电极；（8）合金退火，形成欧姆接触；（9）解理成巴条；（10）腔面膜制备；（11）将巴条解理成单管并置于铟皮上测试。

GaAs 基材料的折射率约为3.5 左右，制得器件自然解理面的反射率接近30%。然而，对于SLD 而言，大幅降低其输出端面的反射率对于抑制器件激射至关重要。

对于λ/4 膜，满足下式时其反射率为零：

其中，n2为所镀制薄膜材料的折射率，n3为入射介质的折射率，n4为基底的折射率。

不难看出，对于GaAs 基SLD，当单层腔面膜材料满足n2≈1.87 时，λ/4 膜厚可以实现1 μm 波段的器件前腔面反射率近似为零。

HfO2薄膜在可见光至近红外波段具有较好光学特性，吸收小、性能稳定，折射率约1.8～1.9，依赖于制备工艺参数。实验基于高真空射频磁控溅射方法，通过溅射功率、基片台温度、腔压及气体流量的优化得到了稳定的折射率约1.87 的HfO2薄膜成膜条件。采用λ/4 HfO2膜作为SLD 前腔面的增透膜，简化了常规多层增透膜工艺的复杂度，并且避免了由于不同材料间的应力问题而导致的薄膜质量较差或薄膜脱落的现象。器件后腔面采用三对Si/SiO2作为高反膜，以提高SLD 的腔内增益长度，实现器件的高功率输出。溅射的典型HR、AR 薄膜的反射率曲线如图13 所示。

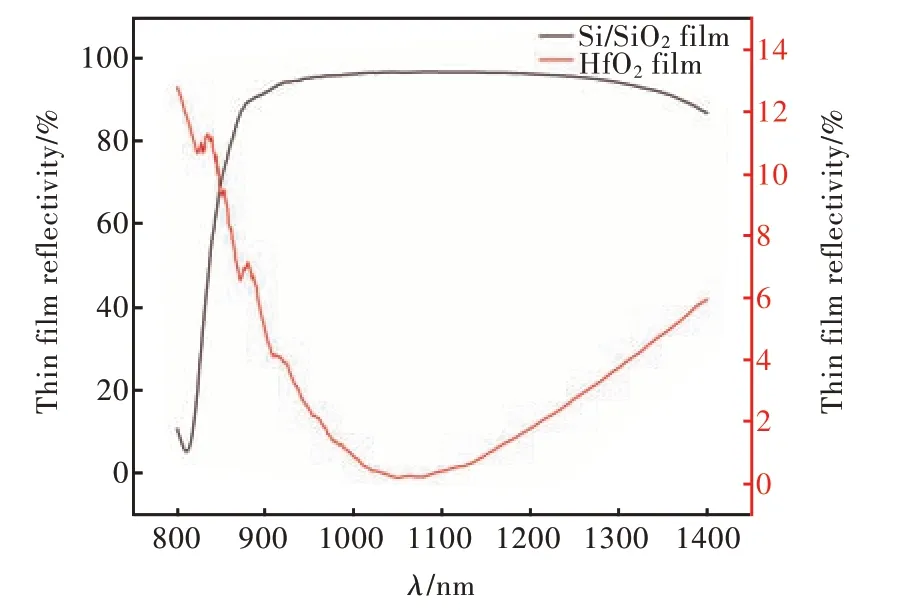
图13 薄膜反射率曲线Fig.13 Thin film reflectance curve

利用上述器件制备工艺，最终制备了曲率半径不同的器件。器件结构参数总结在表2 中。其中器件后腔面镀制薄膜的反射率以及器件直波导长度分别用R和L1表示。需要注意的是，SLD 1、3前腔面未镀增透膜；SLD 2 的前腔面镀制了0.5%的增透膜。

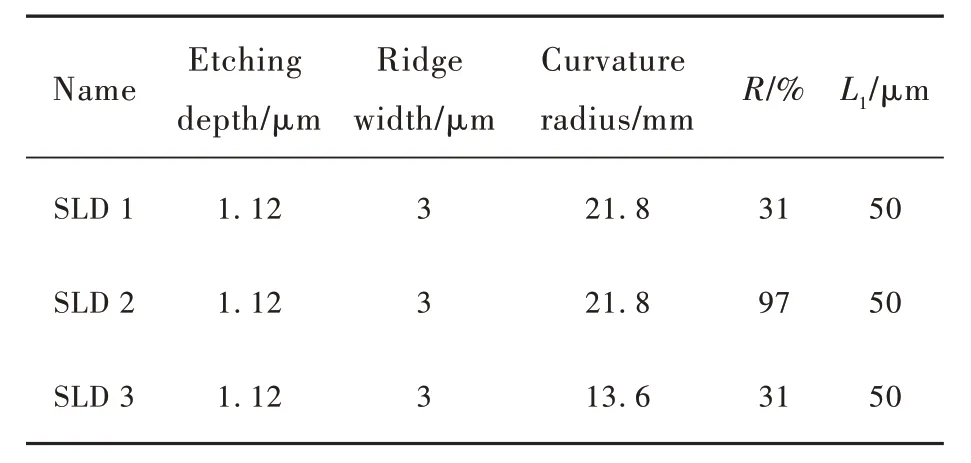
表2 器件结构参数Tab.2 Device structure parameters

3.2 性能测试分析

首先，在脉冲宽度为150 μs、占空比为1.5%的脉冲电流下，对所制备的器件进行了测试。

不同注入电流下各器件光谱如图14 所示，光谱半宽在图15 中给出。SLD 的光谱半宽由自发发射谱与光学增益谱共同决定[13]。低注入电流下，自发辐射占主导地位，光谱半宽较宽。随着注入电流的增加，材料增益增加导致器件总增益增加。与此同时，由于带隙填充效应以及不同量子阱发射光谱叠加，导致材料增益谱半宽变宽。

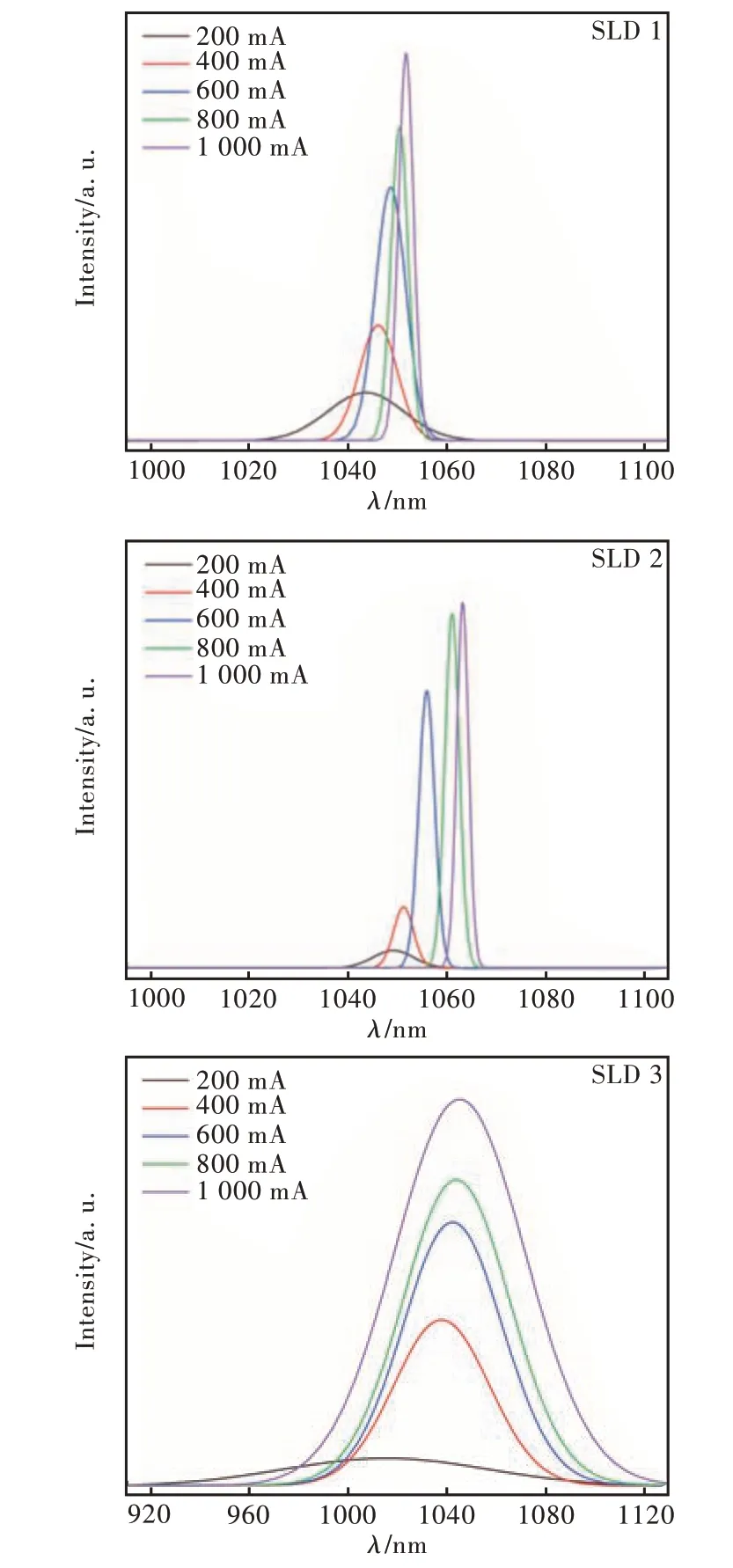
图14 不同脉冲电流下各器件光谱Fig.14 Spectra of various devices under different pulse currents

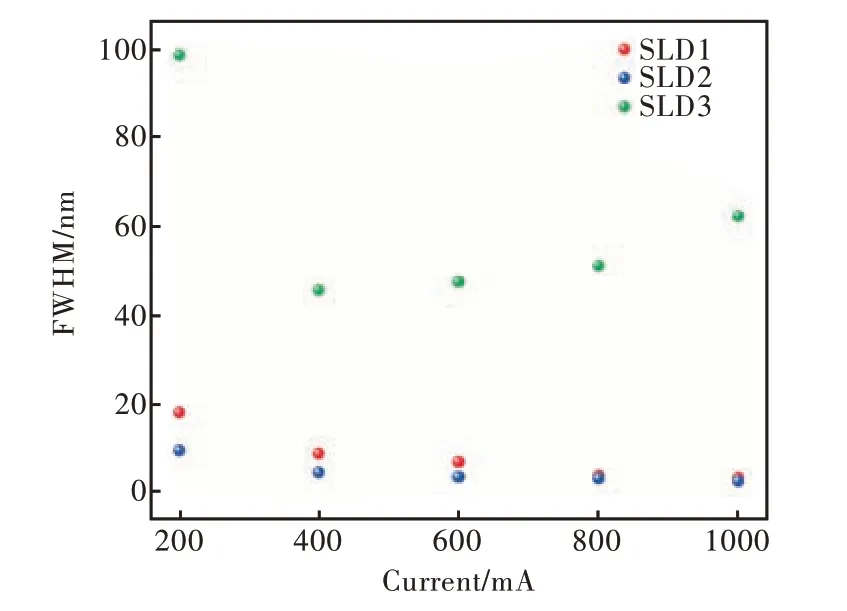
图15 光谱半宽与脉冲电流的关系Fig.15 The relationship between spectral half width and pulse current

不同电流注入下，SLD 光谱半宽的变化趋势可以由下式进行解释[14]：

其中，λ(N)为材料增益谱半宽，G(N)为器件总增益。

SLD 1～2 的损耗系数较小，增益较大。由公式（4）可知，在脉冲电流注入下，器件总增益G(N)的平方根比材料增益谱半宽λ(N)增加得更快，从而导致器件光谱半宽随注入电流的增加而减少。SLD 3 则与之相反。

SLD 2 后腔面镀制了反射率为97% 的高反膜，导致其光谱半宽比SLD 1 更窄。这是由于光在SLD 腔体内传输时，经历了光增益过程，这种增益过程对不同波长的光是不同的。发射光谱中心波长经历的增益最大，远离中心波长的光获得的增益呈现抛物线型递减[15]。SLD 2 的后腔面有更多的光反射回腔内，使光谱中心波长获得的增益更大，光谱半宽变窄，但较低反射率的单层HfO2增透膜的镀制保证了器件并没有在如此高的增益下激射。SLD 3 的损耗较大，根据公式（4）可知，器件增益较小，导致其光谱宽度宽于SLD 1～2。

SLD 的P-I特性曲线如图16 所示。可以看出，器件具有“软阈值”特性。在软阈值以下以自发辐射为主，软阈值以上以超辐射为主[15]。由于SLD 3 的损耗较大，其在较大的软阈值后开始超辐射输出。器件输出功率均随注入电流的增加而增大，这是由于随着注入电流的增加，材料增益增加，输出功率增大。

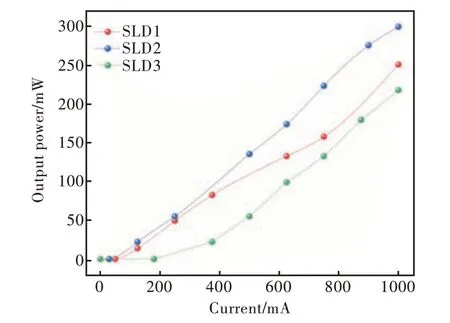
图16 输出功率与脉冲电流的关系Fig.16 The relationship between output power and pulse current

在脉冲电流注入下，SLD 1～2 的输出功率明显大于SLD 3 的输出功率，这是由于SLD 3 的曲率半径较小，损耗系数相对较大，导致器件输出功率较低。SLD 2 的后腔面镀制了高反膜，传输到后腔面的光更多地被反射回波导内。这部分光在波导内经历双程增益放大，导致器件输出功率增加。这是SLD 2 的输出功率大于SLD 1 的原因。

其次，对SLD 2～3 在直流条件下进行了测试。不同连续电流注入下的器件光谱如图17 所示，光谱半宽在图18 中给出。

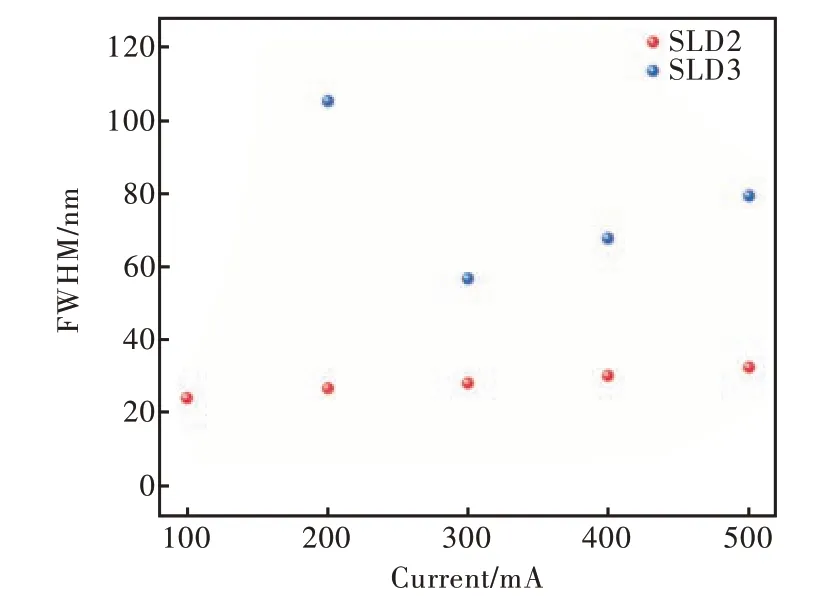
图18 光谱半宽与连续电流的关系Fig.18 The relationship between spectral half width and continuous current

器件在连续电流注入下，获得的增益相对较小。因此在整个测试电流范围内，SLD 2 光谱半峰宽随注入电流的增加而增加且SLD 2～3 的光谱半峰宽均明显宽于脉冲电流下测试的结果。SLD 3 在500 mA 连续电流注入下实现了79.6 nm 的光谱半峰宽。

连续电流注入下的SLD 的P-I特性曲线如图19 所示。与脉冲电流注入的情况相比，器件在连续电流注入下会产生更多的热量，增益相对较小，导致连续电流注入下的输出功率明显小于脉冲电流注入的情况。SLD 2 在500 mA 连续电流下，实现了118.1 mW 的输出功率和32.5 nm 的光谱半宽。

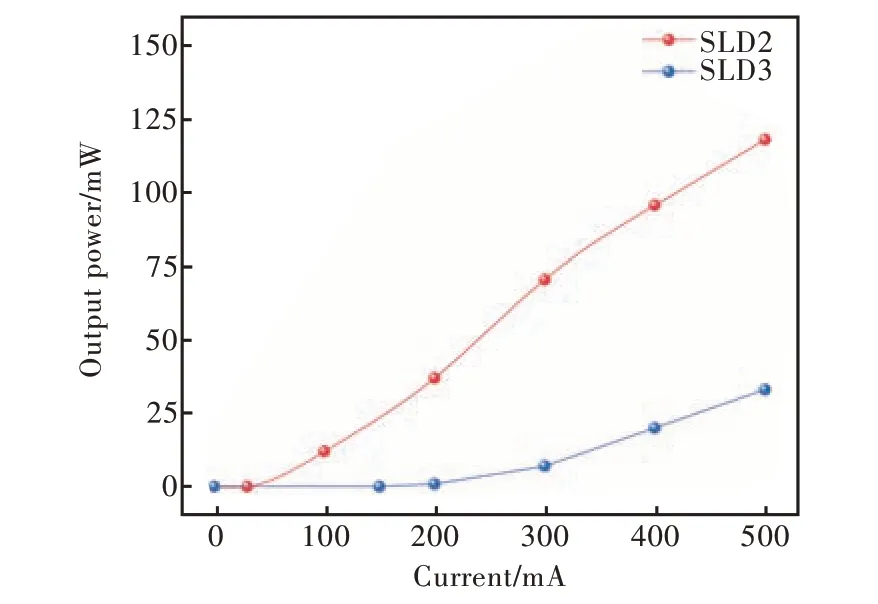
图19 输出功率与连续电流的关系Fig.19 The relationship between output power and continuous current

SLD 的谱宽功率积（PBW）KPBW可以由下式给出[14]：

其中，Pout为输出功率，ΔλFWHM为光谱半宽。图20 给出了制备的SLD 的谱宽功率积随注入电流的变化情况。由于输出功率是外加注入电流的指数函数，在脉冲电流注入下，即使SLD 2 的光谱半峰宽随注入电流的增加而减小，其谱宽功率积仍随注入电流的增加而增大。而在连续电流注入下，SLD 2～3 的光谱半峰宽与输出功率均随注入电流的增加而增加，因此其谱宽功率积也随注入电流的增加而增大。在连续电流注入下，小曲率（R=21.8 mm）的器件可以产生更宽的光谱半宽，导致脉冲电流注入下SLD 2 的谱宽功率积比连续电流注入时小。而曲率半径较小（R=13.6 mm）的器件在脉冲电流下可以实现更高的输出功率，其在脉冲电流下的谱宽功率积大于连续电流注入条件。制备的曲率半径为13.6 mm的器件在脉冲电流注入下实现了13 603.2 mW·nm 的谱宽功率积，在连续电流注入下谱宽功率积达到2 634.8 mW·nm。曲率半径为21.8 mm的器件在连续电流注入下获得了3 838.3 mW·nm 的谱宽功率积。该结果优于Ohgoh 等[4]的报道水平。

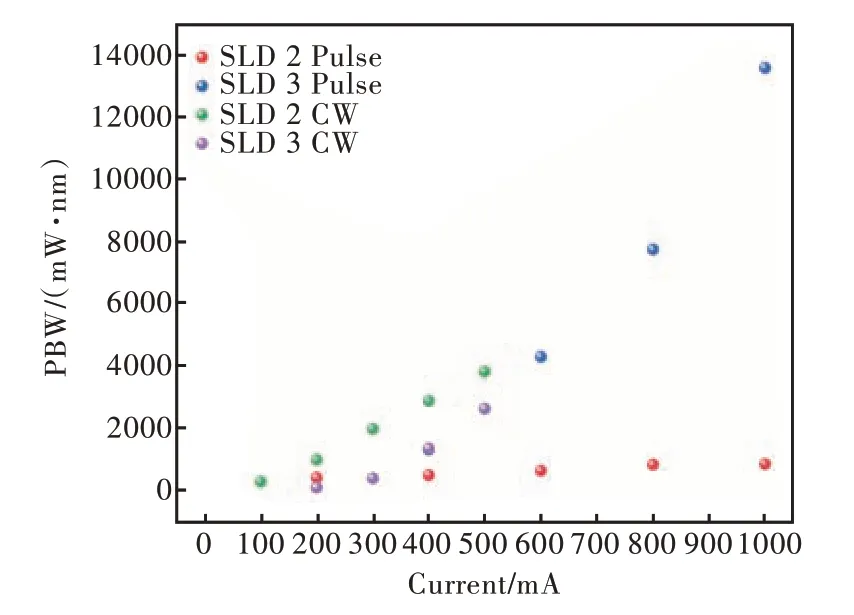
图20 器件在不同电流注入下的谱宽功率积Fig.20 Spectral width and power product of devices under different current injections

器件的远场发散角如图21 所示，图22 为其在1 A 脉冲电流注入下的光斑形貌。从图中可以看出，SLD 1、3 在1 A 脉冲电流注入下均保持基模工作。

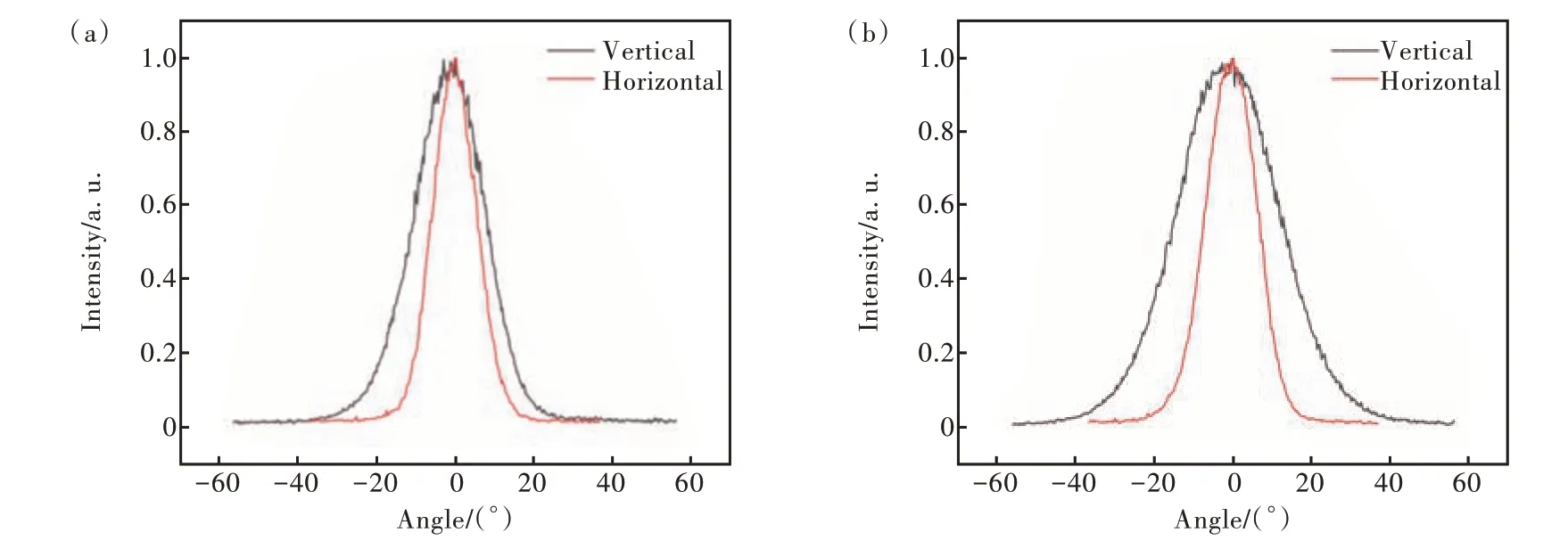
图21 器件远场发散角。 （a）SLD 1；（b）SLD 3。Fig.21 Far-field divergence angle of different devices. （a）SLD 1. （b）SLD 3.

图22 器件光斑形貌。 （a）SLD 1；（b）SLD 3。Fig.22 Spot morphology of different devices. （a）SLD 1．（b）SLD 3.

SLD 1 的水平和垂直远场发散角分别为13.2°和21.1°。由于其曲率半径较大，远场光斑呈现出类似于激光器的“椭圆”状；SLD 3 的水平和垂直远场发散角分别为15.1°和30.4°。由于其曲率半径较小，远场光斑略成“弯月”状。较小的垂直远场发散角以及良好的光束方向性可以使器件与单模光纤耦合效率显著提高。

4 结 论

本文对外延结构进行设计并仿真了J 型波导不同结构参数对损耗系数的影响。基于仿真结果，确定器件结构参数并对电极窗口制备工艺以及单层氧化铪增透膜的成膜条件进行优化，制备出了非均匀阱宽大阱深的三量子阱结构的不同曲率半径的SLD。研究表明，缩小波导层和限制层AlGaAs 材料中Al 组分差值有利于降低器件远场发散角。此外，增加刻蚀深度、脊宽及曲率半径都会使损耗系数减小以提高器件输出功率。通过对氧化铪薄膜成膜条件的摸索，制备出反射率接近0.5%的增透膜，单层增透膜的设计及应用极大地简化了工艺复杂度并避免由于不同材料间的应力问题而导致的薄膜质量较差或易脱落的现象。根据研究结果，研制出波导曲率半径为21.8 mm、腔长约2 mm 的器件，器件前腔面镀制单层氧化铪增透膜，后腔面镀制高反膜，在500 mA 连续电流下，实现了118.1 mW 的输出功率和32.5 nm 光谱半宽。制备的SLD 1 的水平和垂直远场发散角分别为13.2°和21.1°，有利于提高其与单模光纤的耦合效率。

本文专家审稿意见及作者回复内容的下载地址：http://cjl. lightpublishing. cn/thesisDetails#10.37188/CJL.20230216.