怎样做能更好地理解“百分数变化幅度问题”
□陶玲慧
“百分数变化幅度问题”是连续求一个数增加、减少百分之几的问题,难点在于作为初始单位“1”的量是个未知量,同时随着连续的增减变化,单位“1”也会随之发生变化。怎么做可以帮助学生理解其中的变化?可采用以下教学环节。
一、自主探究,初步感知
1.呈现问题,理解题意
教师出示题目:“618”活动期间,某网络书店推出以下活动,全套“哈利·波特”系列(共7册)6月份比5月份降价20%。活动结束后,7月份比6月份又涨价20%。7 月份与5 月份相比,价格是涨了还是降了?变化幅度是多少?
让学生读题,理解题意。
2.提出猜想,计算验证
教师提问:你认为价格变了吗?为什么?
有部分学生认为价格没变,因为先降价20%,再涨价20%,正好抵消;也有部分学生认为6 月份降价的20%和7月份涨价的20%所对应的单位“1”不同,价格会发生变化。
让学生尝试计算,他们会运用如图1中的几种计算方法。
3.方法比较,寻找共性
教师提问:比较上面的三种计算方法,你有什么发现?
学生发现单位“1”在发生变化,6 月份降价的20%是指5月份价格(作为单位“1”)的20%,7月份涨价的20%是指6 月份价格(作为单位“1”)的20%。不管5 月份的具体价格是多少,7 月份的价格都是5 月份价格的96%,算式为:1×(1-20%)×(1+20%)=96%。
二、改变顺序,寻找异同
1.改变条件,再次猜想
教师呈现更改顺序后的题目:“618”活动期间,某网络书店推出以下活动,全套“哈利·波特”系列(共7册)6月份比5月份涨价20%。活动结束后,7月份比6月份又降价20%。7月份与5月份相比,价格是涨了还是降了?变化幅度是多少?
预设有部分学生认为价格会下降,有部分学生认为价格会上涨。
让学生先独立计算,再同桌交流,教师选取不同的方法进行展示。学生发现不管是先降后涨,还是先涨后降,现价与原价相比都是降价,现价是原价的96%,算式为:1×(1+20%)×(1-20%)=96%。
2.两式对比,发现规律
教师呈现两个算式(如图2),并提问:为什么现价都是原价的96%?学生通过观察对比发现:只是更改了(1-20%)和(1+20%)的计算顺序,因此结果是相同的。

图2
3.对比思考,探寻本质
教师引导学生思考:为什么7月份的价格都比5月份低?
让学生先独立思考,再四人小组讨论。
先讨论“先降后涨”的情况:发现5 月份的价格>6月份的价格,5月份降价的20%>6月份涨价的20%,即降价的量>涨价的量。教师根据学生的交流回答完成板书,如图3所示。
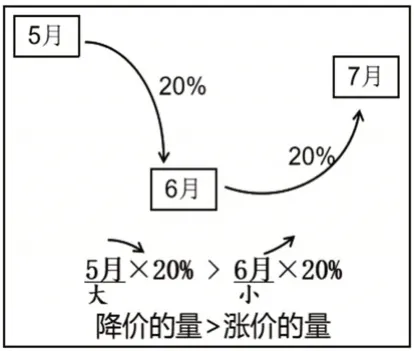
图3
再讨论“先涨后降”的情况:发现5 月份的价格<6月份的价格,5月份涨价的20%<6月份降价的20%,即涨价的量<降价的量。教师根据学生的交流回答完成板书,如图4所示。
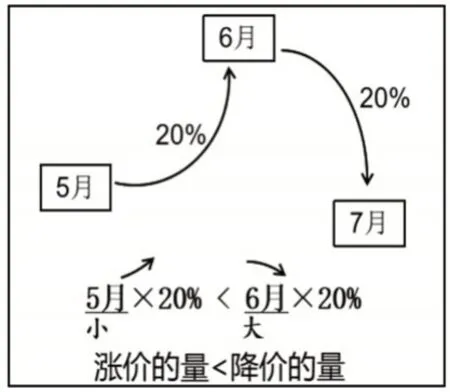
图4
学生通过分析发现:不管是哪种情况,都是“降价的量>涨价的量”,所以7月份的价格都比5月份的价格低。
以上教学过程,从不同的视角帮助学生进行多层次的思考,引导学生在计算、观察、对比中探索数学的一般规律,揭示数学的本质,建立知识之间的联系,优化思维的过程。


