如何利用分割法、拼补法求组合图形的面积
□董周涛
计算组合图形的面积是在学生掌握了平行四边形、三角形、梯形等基本图形的面积计算公式后的综合应用。如何利用分割法、拼补法求组合图形的面积,帮助学生感悟转化思想、发展空间观念呢?可以设计如下教学过程。
一、操作感知,分类提炼
1.自主探究
教师出示题目:求图1中草坪的面积,画一画,算一算,把能想到的方法都记录下来。
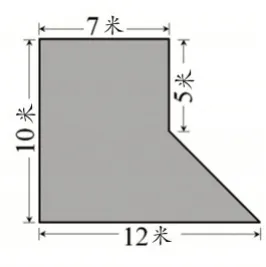
图1
2.交流汇报
让学生展示不同的思考方法(如图2),并交流:①添加的辅助线的位置在哪里?②转化成什么图形?③转化后的图形根据哪些信息求面积?
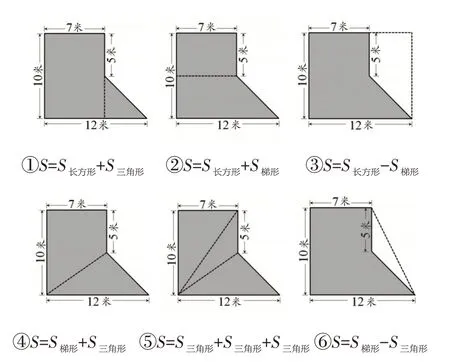
图2
3.比较方法
通过交流,学生发现:不管用哪种方法,计算结果都是82.5平方米。(教学过程略)
教师进一步引导学生思考:不同方法之间有什么联系和区别?
学生发现:就像方法⑤可以优化为方法④,所有方法都是将未知的不规则图形转化为已知的基本图形后求面积的。
4.方法提炼
根据不同的方法进行分类:一类是先将原图分割成基本图形,再相加求得组合图形的面积,如方法①、方法②、方法④、方法⑤,称为“分割法”;另一类是将原图先拼补成一个基本图形,再相减得到组合图形的面积,如方法③、方法⑥,称为“拼补法”。利用分割法、拼补法能巧妙求得组合图形的面积。
二、审辨说理,反思修正
1.观察分析
图3是佳佳解决这个问题的过程,你同意佳佳用的计算方法吗?

图3
2.审辨说理
学生判断出佳佳用的计算方法有误后,引导全班讨论、审辨,发现错误的原因为A、C、D三点不在同一条线段上,图形ACDE不是三角形而是四边形。
3.反思修正
为了得到正确的结果,有学生提出继续分割图形,连接CE,将整个图形分割成三个三角形,再进行计算(如图4)。

图4
三、变式应用,能力提升
1.独立思考
教师出示题目:计算图5中各图阴影部分的面积。

图5
2.汇报交流
(1)关注整体:第①题引导学生整体观察,发现ABCD是一个梯形,直接用公式计算面积,突出对图形整体的把握。
(2)关注细节:第②题引导学生抓住关键细节45°和直角,尝试用拼补法将组合图形转化为等腰直角三角形CDH和等腰直角三角形ABH,并计算面积差(如图6)。
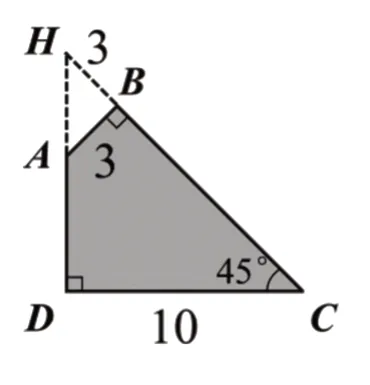
图6
(3)关注联系:第③题引导学生巧妙利用图形边和角的特征,先分割再拼补,将直角三角形BCE旋转至直角三角形BAF的位置,从而将组合图形转化为一个正方形(如图7)。
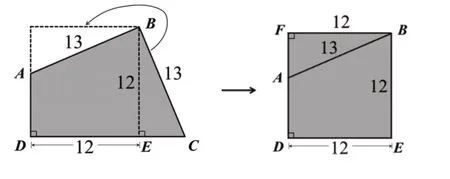
图7
以上教学过程,学生在操作和分类中提炼方法,在审辨和反思中深入理解计算方法,在变式和拓展中提升能力,有效构建了解决组合图形面积问题的基本方法,发展了空间观念。

