基于LSO-RF模型的阶跃型滑坡位移速率预测方法

黄智杰, 简文彬, 夏昌, 赖增荣, 林立鹏

(1. 福州大学紫金地质与矿业学院, 福建 福州 350108; 2. 地质工程福建省高校工程研究中心, 福建 福州 350108; 3. 福州市规划设计研究院, 福建 福州 350108)

0 引言

滑坡是一种严重的自然灾害, 发生时, 严重危害人类的生命财产安全[1-2]. 近年来, 对滑坡进行监测预警已成为一个重要的研究热点, 许多学者在相关方面展开了许多卓有成效的研究[3-7], 其中主要一方面可集中于对滑坡的变形趋势进行预测, 而后在其基础上进行预警. 林世权等[8]通过平均值影响法筛选出藕塘滑坡的诱发因素, 并使用BP神经网络预测该滑坡位移; 王伟等[9]利用粒子群优化算法(particle swarm optimization, PSO)优化后的最小二乘支持向量机模型对大华滑坡的周期项位移建模预测; 岳强等[10]通过小波分析和BP神经网络对郑家大沟滑坡位移进行预测等. 上述研究虽取得了较好的效果, 但多集中于对滑坡的累积位移进行预测, 而对滑坡位移速率进行预测的研究则相对较少. 相比较滑坡累积位移, 位移速率指标更直观, 可通过对位移速率划分等级等方式, 更好地运用于滑坡的预警中[11-12].

阶跃型滑坡是指一种在累积位移上呈现出阶跃段与平稳段交替变化的滑坡[13-14], 其位移速率常常呈现出从接近于零处突然增大的现象, 给其预测造成困难. 此外滑坡是一个复杂的系统, 受到多因素的共同作用, 在利用人工智能模型进行预测时, 合理选择输入特征将直接影响着预测的准确性[15].

随机森林(randomforests, RF)模型是机器学习集成类算法的代表, 其具有控制模型过拟合等优势, 可提高预测的精度. 狮群优化算法(lion swarm optimization, LSO)是一种新型智能优化算法, 具有寻优能力强、 收敛速度快等优点. 为提高阶跃型滑坡位移速率预测的准确性, 本研究以福建省泉州市安溪县尧山村阶跃型滑坡为例, 通过斯皮尔曼相关系数同灰色关联度结果相结合的方法, 筛选出该滑坡影响位移速率的特征, 输入至随机森林模型中, 并通过LSO对模型参数寻优, 实现对阶跃型滑坡位移速率的准确预测.

1 理论与方法

1.1 斯皮尔曼相关系数与灰色关联度

斯皮尔曼相关系数是用于表征两列数据相关性程度的指标, 相较于常见的皮尔逊相关系数, 其对数据要求的条件更低、 适用的范围更广. 灰色关联度分析方法是根据因素之间发展趋势的相似或相异程度来衡量因素间关联程度的一种方法. 根据滑坡各因素监测数据间非线性等特点, 文中综合使用斯皮尔曼相关系数和灰色关联度分析进行滑坡位移速率预测模型的输入特征筛选.

1.2 LSO-RF耦合模型

1.2.1随机森林算法

随机森林算法是一种基于决策树的集成学习模型[16], 它能随机选择数据样本和特征来训练多个决策树, 并通过取平均值等方式提高模型准确性和泛化能力. 由于随机森林算法具有能减少模型过拟合、 运行速度快等优点, 本研究选用随机森林模型作为预测耦合模型的一部分. 该算法对样本i的预测流程如图1所示.

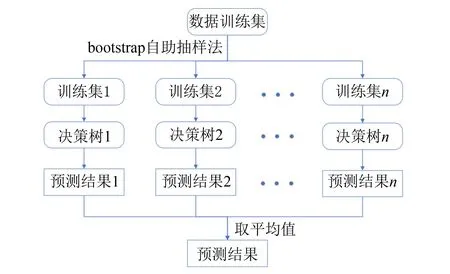
图1 随机森林算法预测流程图Fig.1 Prediction flowchart of random forest algorithm

1.2.2狮群优化算法

LSO算法是一种基于自然界中狮群行为特征的启发式优化算法. 与传统的优化算法不同, 该算法通过模拟狮子狩猎时的合作行为来实现全局最优解的搜索[17]. 因LSO算法具有鲁棒性强、 避免陷入局部最优解等优点, 通过该算法对随机森林模型中关键参数进行寻优, 以找到模型参数的最佳组合.

本研究预测方法的总流程见图2. 首先, 由滑坡监测站及附近气象资料获取日降雨量、 日均孔隙水压力、 位移速率、 地表径流等数据; 其次, 分别计算滑坡位移速率与其余指标的斯皮尔曼相关系数和灰色关联度, 选取两者均较优的结果与滑坡历史位移速率共同作为RF模型的输入特征; 最后, 通过LSO算法对RF模型参数进行寻优以提升模型的预测精度.

图2 预测方法流程图Fig.2 Flowchart of the forecasting method

2 实例分析

2.1 工程地质概况与位移速率分析

尧山滑坡位于福建省泉州市安溪县西坪镇尧山村境内[18]. 滑坡后缘横向宽约80 m, 前缘宽约200 m, 纵向长约350 m, 前后缘高差约115 m, 滑坡体坡度约为20°～25°, 面积约5.2×104m2, 体积约5.0×105m3, 滑动面深度约为10～13 m, 且滑坡后缘拉张裂缝发育, 主滑面工程地质剖面图见图3. 自2019年8月起, 对该滑坡进行自动化监测, 获取了该滑坡监测站1与监测站2的深部水平位移、 深部孔隙水压力、 日降雨量等时间序列数据. 滑坡边界及监测站布置图如图4所示.

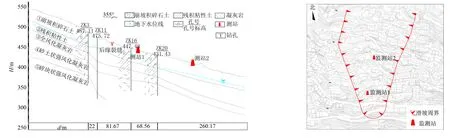
图3 研究区滑坡主滑面工程地质剖面图 图4 滑坡周界及监测站示意图Fig.3 Engineering geological profile of the main landslide surface within the study area Fig.4 Schematic diagram of landslide perimeter and monitoring points

因监测站1位移大, 站2位移相对较小, 故此次选择监测站1滑面附近处埋深为12 m的位移数据及埋深10 m的孔隙水压力数据为代表进行分析. 滑面附近处位移与滑动面处位移在数值上存在差异, 且由于监测仪器埋设的问题, 这种误差可能会加大, 但两者在趋势上相符. 因此将上述埋深12 m的累积位移视为滑坡的相对累积位移、 由相对累积位移所确定的位移速率称为滑坡的相对位移速率(后文为方便表述, 统称为累积位移s和位移速率v). 为分析该滑坡位移特点, 2021年2月25日—7月25日时间段内滑坡的累积位移、 位移速率、 日降雨量情况如图5所示.

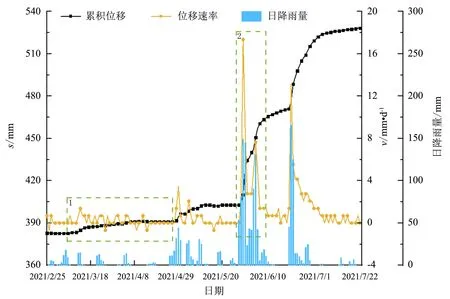
图5 滑坡累积位移、 位移速率、 日降雨量关系图Fig.5 Relationship among cumulative displacement, displacement rate and daily rainfall

由图5可知, 该滑坡受降雨影响明显. 在无雨或少雨期间, 滑坡处于平稳段(如图5中虚线框1), 位移速率较小且变化缓慢(基本为0～0.7 mm·d-1); 而在连续大雨期间, 滑坡处于阶跃段, 位移速率会迅速上升(如虚线框2中速率突升到17.36 mm·d-1)并在雨停一段时间后回落至平稳段. 这些特点会导致许多人工智能模型因学习到平稳段大量数据的规律而产生过拟合, 对阶跃段数据的预测效果不佳. 因此, 在预测该类滑坡位移速率时, 需要选择适合的人工智能模型.

2.2 基于斯皮尔曼相关系数和灰色关联度的特征选择

为实现较好地预测效果, 需要挑选与预测目标相关性程度高的数据作为模型输入特征. 首先探究位移速率与其他因素的相关性. 由于这些时间序列之间的关系不是严格意义的线性关系, 如图6, 因此采用斯皮尔曼相关系数进行分析, 结果详见表1.

表1 位移速率与其余因素间相关性Tab. 1 Correlation between the displacement rate and the remaining factors

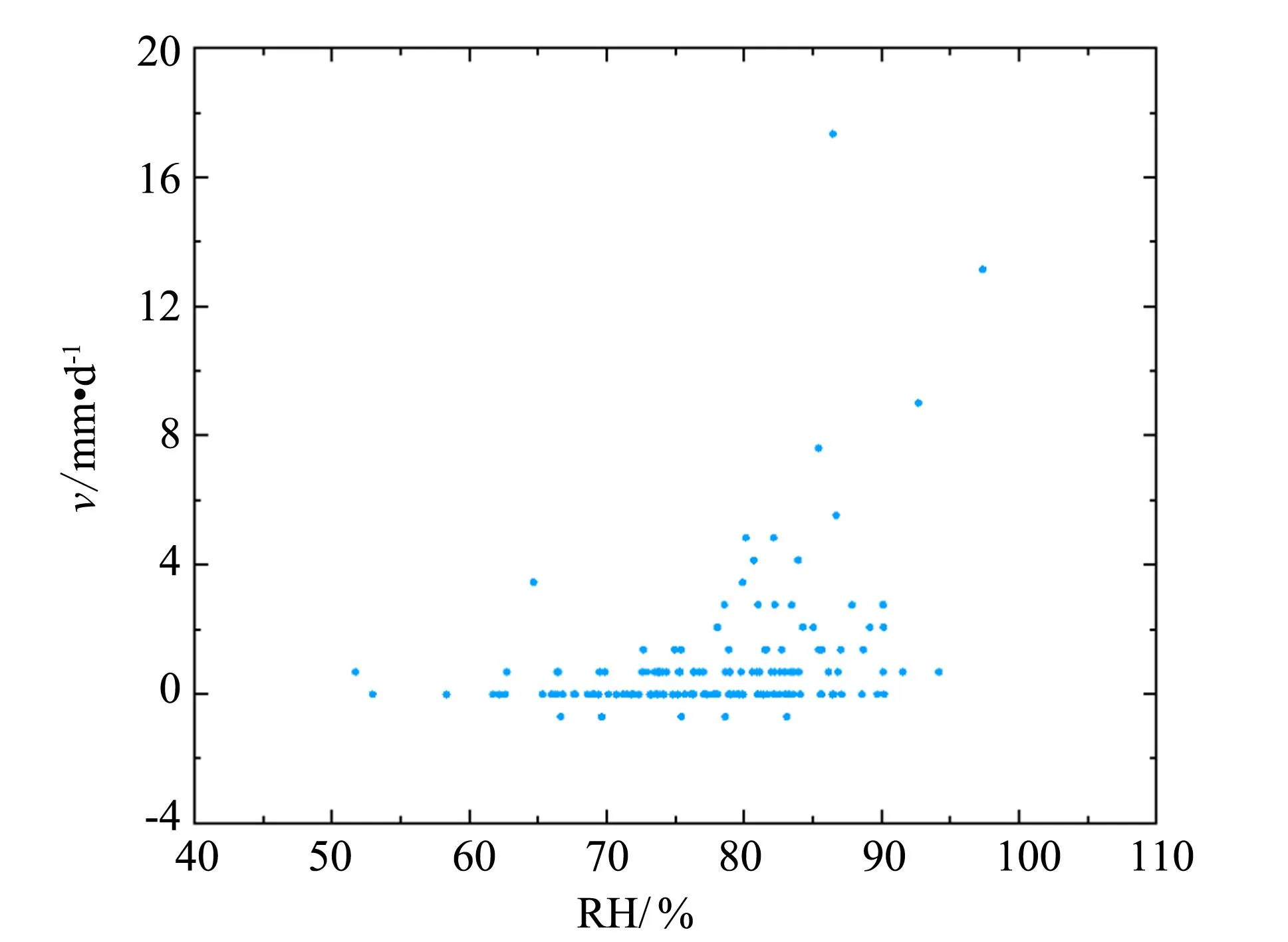
图6 位移速率与相对湿度散点图Fig.6 Scatter plot of displacement rate and relative humidity

此外, 为了判断滑坡系统中各因素对位移速率的影响, 计算位移速率时间序列与其他因素时间序列的灰色关联度(分辨率ρ取0.5), 结果见表2.

表2 位移速率与其余因素间灰色关联度Tab.2 Gray correlation between the displacement rate and the remaining factors

在选取输入特征方面, 从斯皮尔曼相关系数角度来看, 日均孔隙水压力、 土壤有效持水量与位移速率之间的相关性排名分别为第一和第二, 相关性较高; 从灰色关联度角度来看, 日降雨量、 地表径流与位移速率之间的关联度排名分别为第一和第二, 关联度较高; 如综合两者结果来看, 位移速率只有同日降雨量、 日均孔隙水压力的相关性和关联度均较高. 本研究所提方法为综合斯皮尔曼相关系数和灰色关联度排名, 选择两者排名均较前的因素作为输入特征. 为验证该方法的优越性, 采用随机森林模型比较上述不同特征选择方法所确定的输入特征对预测效果的影响. 3种特征选择方法对应的输入特征组合分别为: 1) 日均孔隙水压力、 土壤有效持水量(斯皮尔曼相关系数角度选取); 2) 日降雨量、 地表径流(灰色关联度角度选取); 3) 日降雨量、 孔隙水压力(本研究所提特征选择方法选取). 模型的训练集为2021年2月25日—6月9日期间的数据, 模型的测试集为2021年6月10日—7月25日期间的数据, 预测结果见图7.

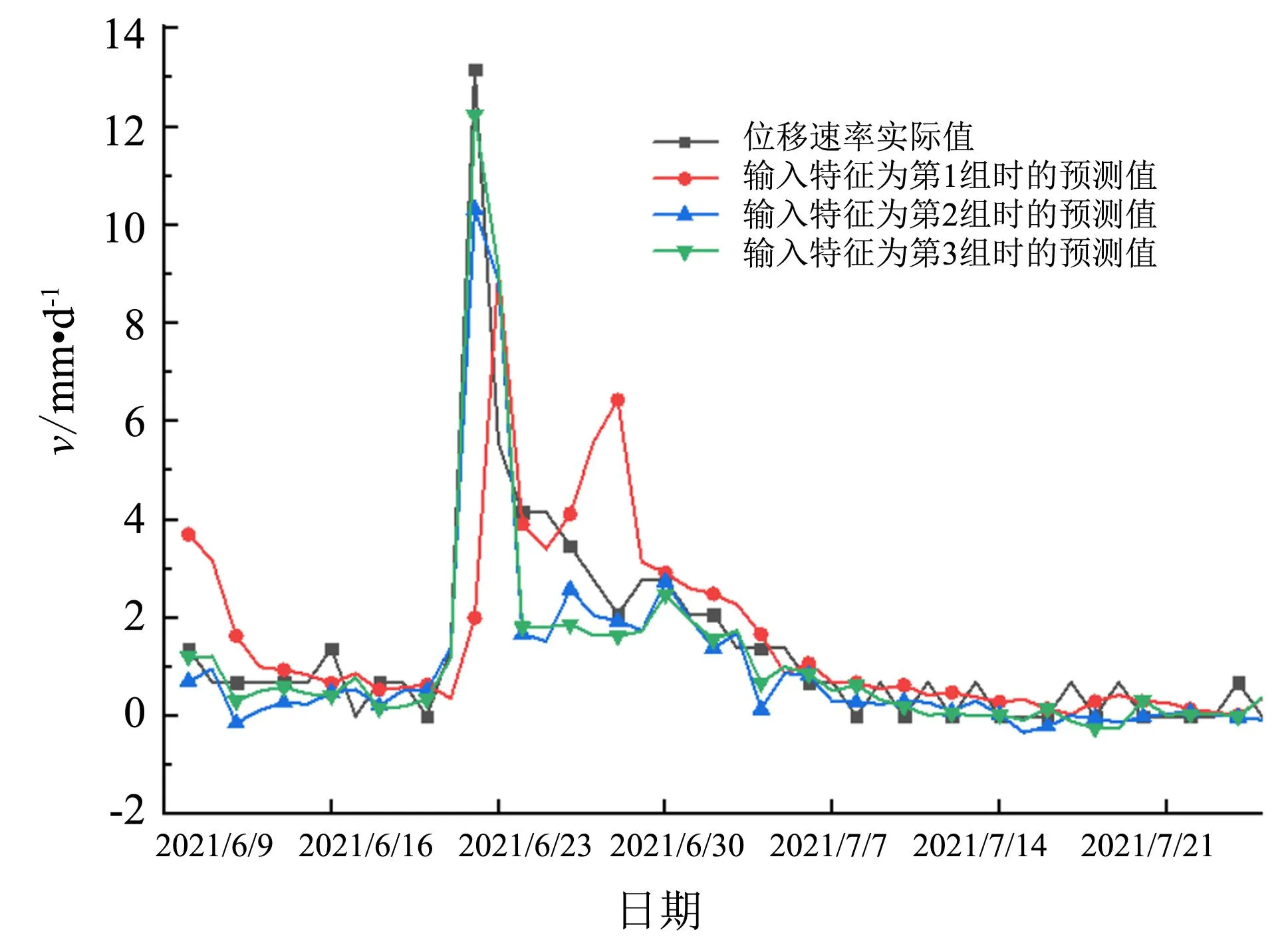
图7 不同组合作为输入特征时模型的预测效果Fig.7 Prediction effect of the model when different combinations of input features are used

从图7中可以看出, 选择第3组特征组合作为模型输入特征时, 模型的预测效果在三者中最好. 说明本研究所提的特征选择方法筛选出的输入特征能使模型取得更好的预测效果. 分析上述原因, 主要有以下两点: 1) 斯皮尔曼相关系数适用范围虽广, 但个别情况下会因数据不适用(如文中的位移速率与地表径流间的关系非单调), 失去统计意义; 2) 在计算灰色关联度时, 因分辨率取值等原因存在主观性, 会影响到排序的结果.

综上所述, 本研究所提方法, 能最大程度上弥补单独使用斯皮尔曼相关系数或灰色关联度进行特征选择的局限性, 更准确地实现模型输入特征的选择.

2.3 阶跃型滑坡位移速率预测

依据前文所述, 确定日降雨量、 日均孔隙水压力为预测模型的输入特征. 有学者研究表明, 滑坡受自身演化阶段的影响[19], 学习预测目标以前的趋势有助于提升模型的预测精确度. 最终, 本研究将日降雨量、 孔隙水压力、 历史位移速率作为输入特征, 位移速率作为输出特征, 进行模型的训练和预测. 训练集和测试集的划分采用扩展窗口法, 即每预测完一个数据后, 将数据的真实值纳入原有的训练集中, 使模型学习到最新的趋势, 减少模型过拟合.

用Python搭建结合扩展窗口法的RF模型, 表3所列的模型中4个参数会对模型预测结果产生较大的影响, 其初始参数分别设置为300、 2、 1、 4. 采用LSO算法对这4个参数进行调优, 适应度函数为预测结果与真实值之间的平均绝对误差(mean absolute error,EMA)、 均方根误差(root mean square error,ERMS)和拟合优度R2相反数的平均值. 将参数寻优范围分别设为1～1 000、 2～10、 0～0.5、 1～4, 找到的最佳参数见表3. 图8展示了优化前后模型的预测效果.

表3 LSO-RF模型搜索参数的最优值Tab.3 Optimal values of search parameters of the LSO-RF model

图8 LSO算法优化RF参数前后预测结果图Fig.8 Prediction results before and after optimization of RF parameters by LSO algorithm

文中使用EMA、ERMS和R2评估模型预测效果, 使用LSO算法优化参数后, 模型的EMA、ERMS和R2都较优化前好(优化前EMA为0.594,ERMS为0.900,R2为0.829; 优化后EMA为0.560,ERMS为0.829,R2为0.854); 此外, 模型在位移速率峰值附近的预测更加准确(优化前误差为7.0%, 优化后为3.4%). 因此, LSO-RF模型可以在数据集较少的情况下有效地预测阶跃型滑坡的位移速率.

3 预测模型对比分析

为验证LSO-RF模型的预测优势, 本研究将RF模型与SVM、 PLS、 KNN算法进行对比, 结果见图9. 此外, 将分别经过LSO算法和鲸鱼优化算法(whale optimization algorithm,WOA)优化后的RF模型的预测结果同优化前的结果进行对比, 结果见图10. 各模型的EMA、ERMS和R2见表4.

表4 各预测模型的评价指标值Tab.4 Evaluation index values for each forecast model

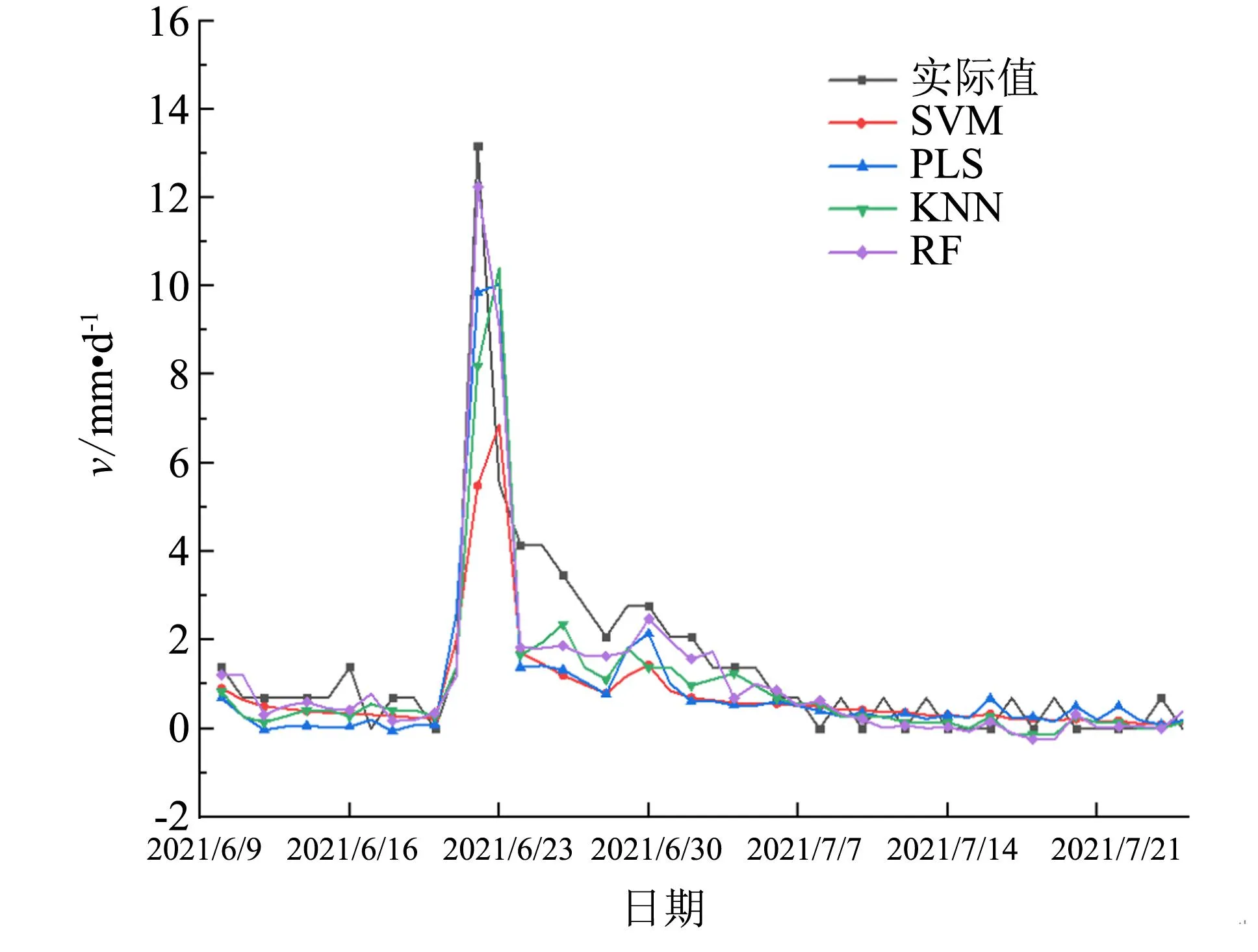
图9 RF模型同常见模型预测结果对比Fig.9 Comparison of prediction results of RF model and common models

从图9中可看出, 各模型在预测平稳段时表现相近, 但在预测阶跃段时表现差异很大. 综合图9和表4, PLS略优于KNN模型, 两者均优于SVM模型, 但它们在预测位移速率峰值时均存在滞后和预测精度不高的问题. 相比之下, 采用RF随机森林模型在预测阶跃段位移速率上表现良好.

如图10和表4所示, 经过LSO算法和WOA优化后, RF模型的预测效果均有提升. 但LSO-RF模型的预测效果较WOA-RF模型更好, 表现为在峰值速率附近的预测误差更小(两者对峰值时刻的预测误差分别为3.4%与4.5%), 以及EMA、ERMS和R2指标更优. 两种优化算法在各迭代次数中的适应度值见图11, 由图11可知, LSO算法比WOA更快地实现了更好的适应度值, 一定程度表明了LSO算法的寻优能力和速度更强.

综上所述, 本研究所建立的LSO-RF模型相较于其它常见模型, 能充分地学习、 提取到训练集中特征的规律, 避免或减少模型的过拟合, 实现利用较少的数据集对阶跃型滑坡位移速率更准确的预测, 且狮群优化(LSO)算法在模型参数寻优上具有一定的优势.

4 结语

1) 提出一种综合考虑斯皮尔曼相关系数和灰色关联度结果的特征选择方法, 用于筛选影响滑坡位移速率的关键因素. 该方法选择的输入特征能够提高模型的预测能力, 相比于单独使用灰色关联度或斯皮尔曼相关系数进行特征选择, 本文提出的方法具有明显的优势.

2) 随机森林算法因其具有较好的泛化能力及处理非线性数据等特点, 相较于常见模型, 能有效解决在阶跃型滑坡位移速率预测中存在的过拟合问题, 实现更好的预测效果, 其较SVM、 PLS、 KNN模型的预测能力有着很大的进步.

3) 使用LSO算法对RF模型参数进行寻优, 可避免主观因素和人工搜索的影响, 实现更好的预测效果. 与WOA算法相比, LSO算法具有更强的优化能力, 所搭建的LSO-RF模型可以更准确地预测阶跃型滑坡的位移速率, 可为同类型滑坡位移速率预测提供参考.