基于CEEMDAN·MPE-NHT的爆破地震波信号时频分析*

孙 苗,吴 静,吴 立,杨钧凯,覃亚男

(1.湖北国土资源职业学院 环境与工程学院,武汉 430090;2.中国地质大学(武汉) a.岩土钻掘与防护教育部工程研究中心;b.工程学院,武汉 430074;3.湖北工程学院 土木工程学院,孝感 432000)

希尔伯特-黄变换(Hilbert-Huang Transform,HHT)由经验模态分解(Ensemble Empirical Mode,EMD)[1]和希尔伯特变换(Hilbert Transform,HT)[2]组成,其中EMD以其能识别数据内在属性并根据数据本身特征进行分解在信号分析领域得到了广泛应用[3]。对EMD分解结果进行Hilbert变换,更是实现了将时域信号转变为频域信号,帮助爆破工程技术人员对爆破地震波信号传播特征、内在属性进行识别,对爆破地震波危害控制起到了一定的指导作用[4-6]。

但EMD对含有噪声的爆破地震波信号相对敏感,而实际爆破地震波监测又无法避免噪声信号的混入[7],这便造成了实际爆破地震波信号EMD得到的固有模态函数(Intrinsic Mode Function,IMF)[8,9]存在严重模态混淆[10-12],而Hilbert变换处理这类IMF分量会产生错误的时频分析结果,这样的结果对爆破地震波危害效应分析意义不大,有时候甚至会成为阻碍爆破工程技术人员作出判断的干扰项。因此如何对HHT处理含噪爆破地震波信号遇到导致分析精度受损的问题进行处理,是目前爆破地震波危害效应分析亟待解决的问题。

鉴于此,对影响EMD-Hilbert时频分析精度的因素进行逐一改进。对EMD进行改进,使其可降低对噪声的敏感性。具体实现通过两步,首先在EMD中添加自适应白噪声,得到自适应补充集合经验模态分解(Complete Ensemble Empirical Mode Decomposition with Adaptive Noise,CEEMDAN)[13-15],用于抵抗监测中混入噪声的低频部分;再者引入多尺度排列熵(Multiscale Permutation Entropy,MPE)[16-18]到CEEMDAN中,充分发挥MPE随机性检测能力,抑制高频噪声对分解精度的影响。以上两步得到的IMF可认为是降噪处理后的IMF,对CEEMDAN·MPE得到的IMF进行归一化Hilbert变换(Normalized Hilbert transform,NHT)[19,20]使得传统的Hilbert变换不受Bedrosian定理的约束,降低负值瞬时频率出现的概率。通过上述三步可实现HHT时频分析精度提升。

最后进行含噪仿真爆破振动信号和实测含噪水下钻孔爆破地震波信号CEEMDAN·MPE-NHT时频分析算法和HHT算法对比研究,以验证CEEMDAN·MPE-NHT算法能有效提高HHT时频精度,得到反映真实爆破振动属性的时频特征参数,对爆破振动特征识别和制定科学的防护措施具有一定的指导作用。

1 CEEMDAN·MPE-NHT时频分析算法

CEEMDAN·MPE-NHT时频分析算法可分两步构建,第一步建立CEEMDAN·MPE算法,其后对CEEMDAN·MPE算法得到的IMF进行NHT。

CEEMDAN·MPE算法的核心是通过剔除噪声来抑制EMD模态混淆。它将MPE的随机性检测功能与CEEMDAN的自适应性相结合,可有效地减少噪声的干扰。有关CEEMDAN和MPE的详细介绍,请参阅文献[13-15]和[16-18]。在这里,仅通过流程图1分析CEEMDAN·MPE的操作过程。

图1 CEEMDAN·MPE算法流程图Fig. 1 CEEMDAN·MPE algorithm flow chart

Hilbert变换得到具有实际物理意义的瞬时频率通常需满足十分苛刻的要求,模态混淆的IMF分量往往不能满足要求。鉴于此Huang等提出NHT[20],以此来提高瞬时频率的计算精度。

NHT的原始操作是对IMF的调频分量进行Hilbert变换,IMF来源是EMD或集合经验模态分解(Ensemble Empirical Mode Decomposition,EEMD)。不难发现,本文得到的IMF物理意义较EMD和EEMD得到的IMF更加清晰,真实性更高。将文献[20]中的IMF替换成CEEMDAN·MPE得到的IMF,便是本文的实现途径。进一步分析,得到CEEMDAN·MPE-NHT时频分析算法运算流程图,见图2。

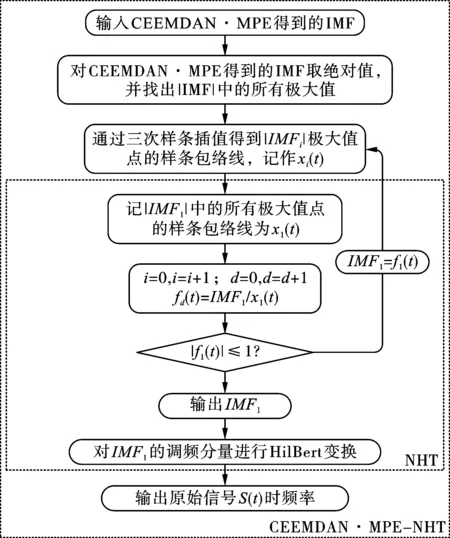
图2 CEEMDAN·MPE-NHT算法流程图Fig. 2 CEEMDAN·MPE-NHT algorithm flow chart

2 仿真信号CEEMDAN·MPE-NHT时频分析

为突出CEEMDAN·MPE-NHT时频分析算法相比HHT可有效提高含噪爆破地震波信号时频特征参数的提取精度,特进行CEEMDAN·MPE-NHT和HHT的含噪仿真振动信号时频分析对比研究。

含噪仿真振动信号S(t)=x1(t)+x2(t),其中x1(t)=wgn(1,N,0.1),即功率为0.1的噪声信号,如图3所示;x2(t)=sin(2×pi×100×t),即频率为100 Hz的正弦信号,如图4所示;仿真信号如图5所示。采样点数N=512,采样时间t=1/N∶1/N∶1。

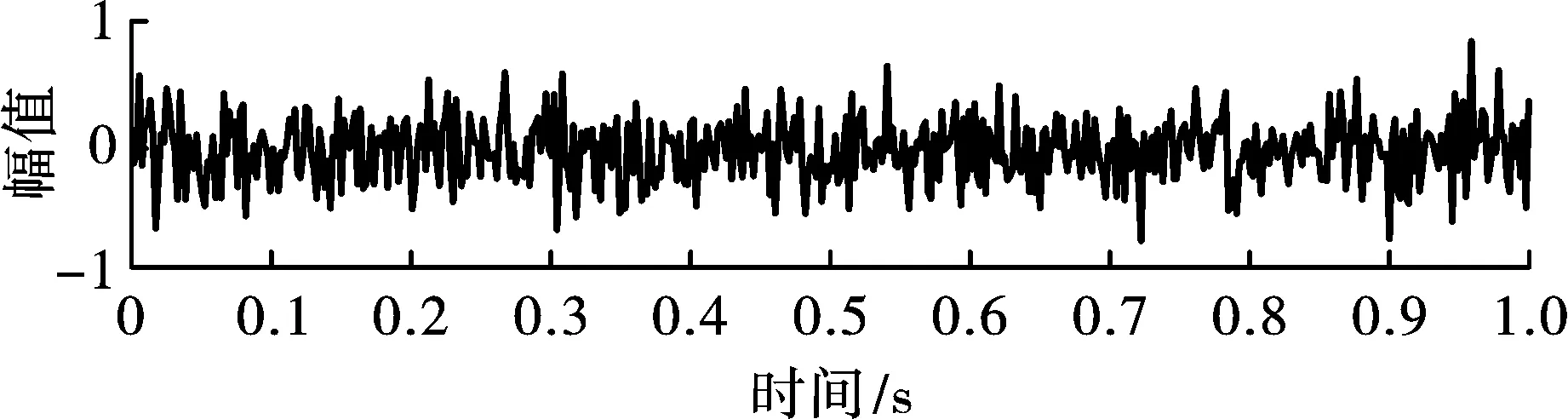
图3 功率为0.1的噪声信号图Fig. 3 Noise signal with power of 0.1

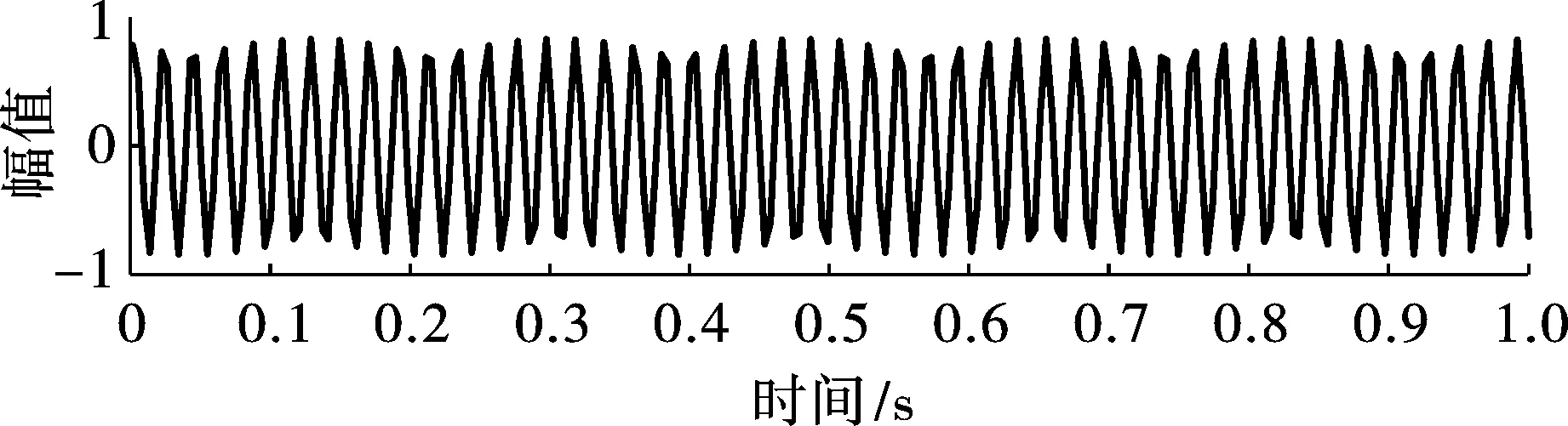
图4 频率为100 Hz的正弦信号图Fig. 4 Sine signal with frequency of 100 Hz

为突出CEEMDAN·MPE对EMD模态混淆的抑制作用,分别采用EMD和CEEMDAN·MPE对S(t)进行模态分解。图6为EMD分解结果,不难发现IMF1是难以除去的噪声信号;高频模态混淆严重,如IMF2在0.53 s,0.64 s及0.85 s附近均出现了高频向中频发散的趋势;中频模态混淆有所缓解,如IMF3在0.41 s及右端点附近存在向低频发展的趋势;低频相对稳定,如IMF5和IMF6。图7为CEEMDAN·MPE分解结果,分解得到的IMF从高频向低频依次排列,未见明显模态混淆现象,模态显示相比EMD结果清晰且稳定。

图7 仿真信号经CEEMDAN·MPE得到的IMFFig. 7 IMFs of simulated signal by CEEMDAN·MPE

为突出NHT对瞬时频率具备清晰物理意义的贡献,进行Hilbert变换和NHT对比分析。对EMD得到的IMF进行Hilbert变换,得到的时频谱见图8。对CEEMDAN·MPE得到的IMF进行NHT,得到的时频谱见图9。

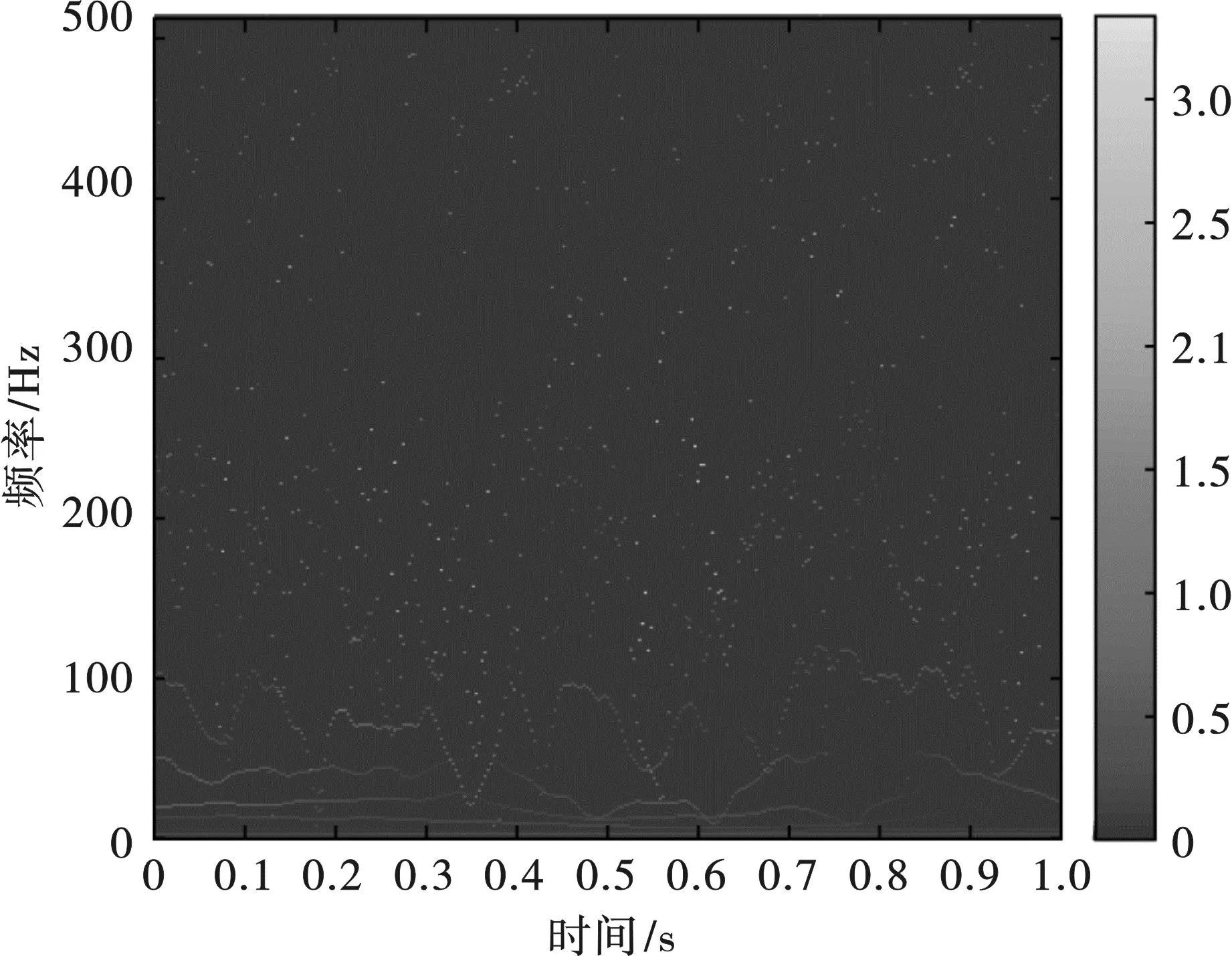
图8 EMD-HT得到的仿真信号时频谱图Fig. 8 Time-frequency spectrum of simulated signal obtained by EMD-HT

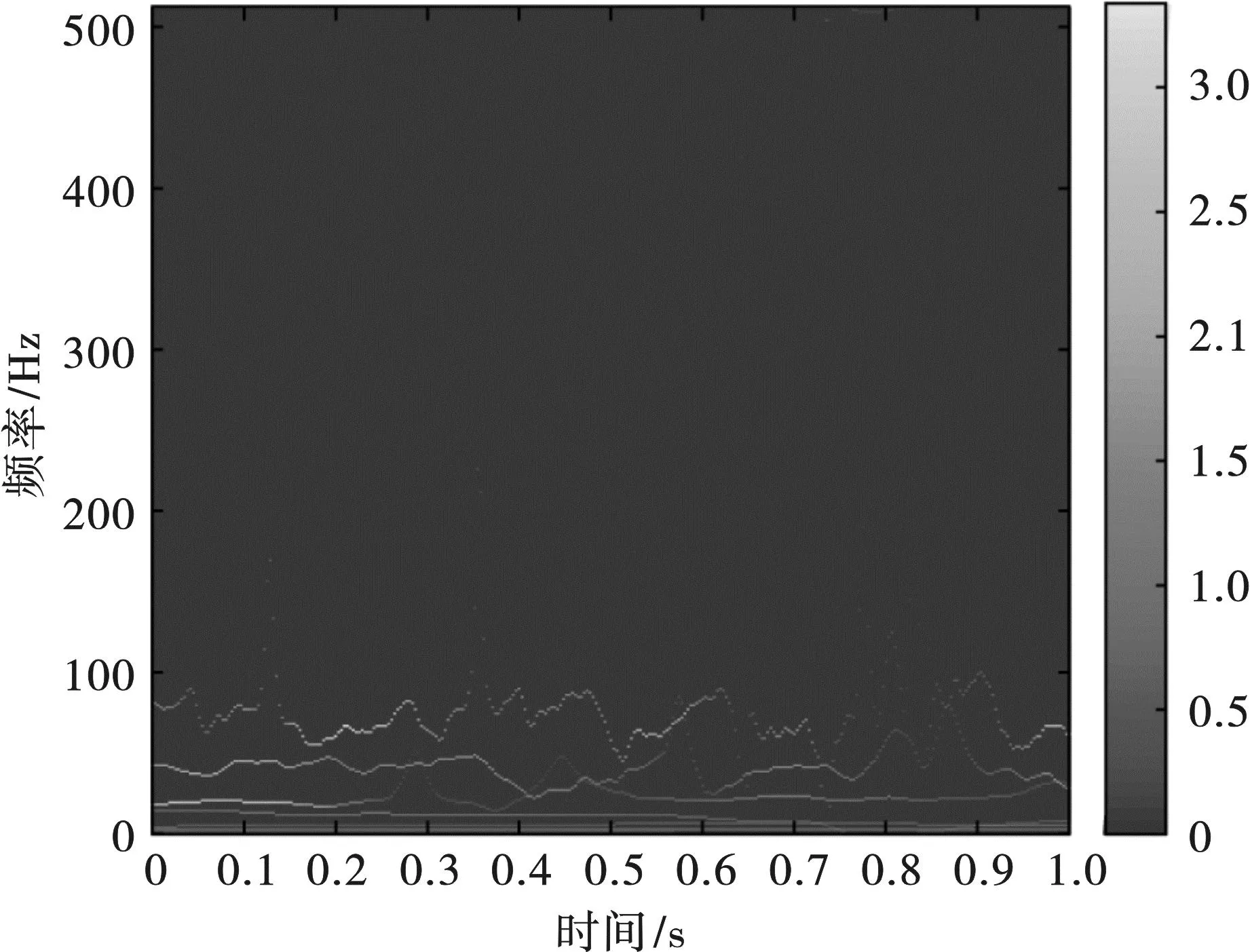
图9 CEEMDAN·MPE-NHT得到的仿真信号时频谱图Fig. 9 Time-frequency spectrum of simulated signal obtained by CEEMDAN-INHT

图8为EMD-HT时频谱,模态混淆分量经Hilbert变换得到的时频谱分辨率不高,出现了100 Hz以上难以识别的虚假分量。图9为CEEMDAN·MPE-NHT时频谱,该算法通过CEEMDAN·MPE来抑制S(t)中的x1(t);CEEMDAN·MPE得到的IMF经NHT处理后得到的频率分布在0～100 Hz,和x2(t)具有对应性,时频参数可清晰识别。侧面说明了CEEMDAN·MPE得到的IMF经过NHT能够得到具有实际物理意义的时频信息,即CEEMDAN·MPE-NHT时频分析算法不仅可有效抑制噪声引起的EMD模态混淆,同时得到时频分辨率双高的信号频谱图。

3 炸礁爆破地震波信号CEEMDAN·MPE-NHT时频分析

以三峡-葛洲坝两坝间莲沱河段航道整治炸礁工程为研究对象,选择下岸溪～丁头镇区间LT5炸礁区为研究对象。该区总的炸礁工程量2561.0 m3,清碴工程量2484.2 m3。LT5区周边环境复杂,炸礁区距离最近的民房70 m、距离公路(陡纸线)81 m,还有滑坡、崩塌和泥石流等不良地质情况,对工程影响较大。

选取炸礁爆破施工期间处于较危险地带的民房作为研究对象,对民房进行现场监测得到一系列监测数据。观察监测数据发现水下钻孔爆破地震波信号三个方向振动速度呈现出有规律的一致性,水平径向峰值振动速度最大,水平切向次之,而垂直方向振动速度最小。考虑文章篇幅,仅对水下钻孔爆破地震波监测信号的水平径向峰值振动速度进行CEEMDAN·MPE-NHT时频分析。有代表性水平径向地震波监测信号如图10所示。

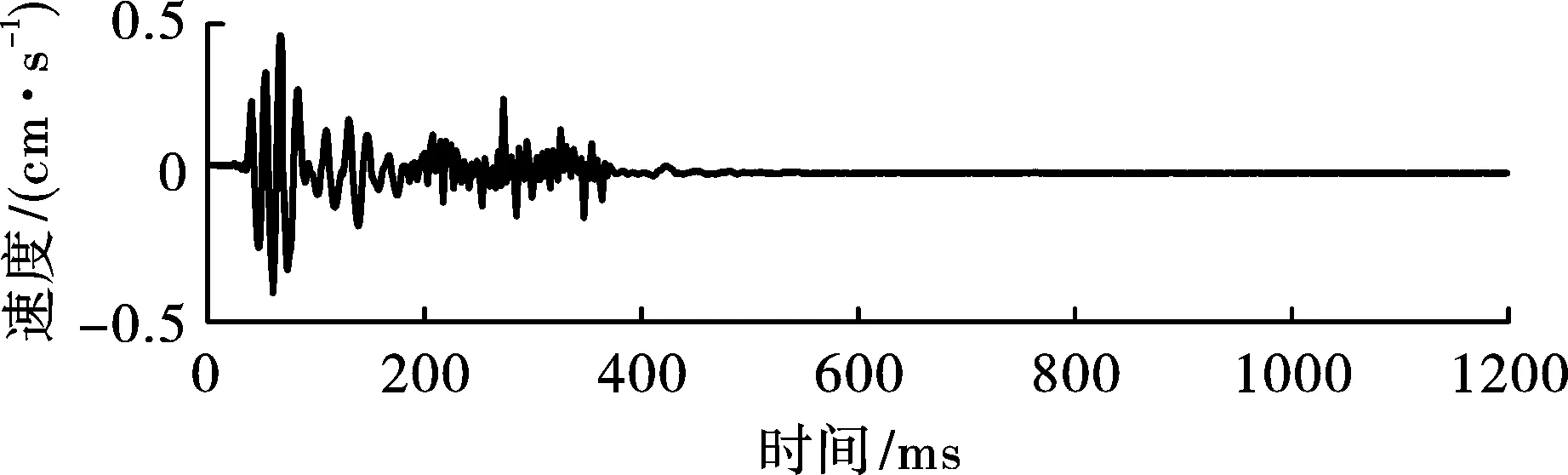
图10 水平径向地震波监测信号波形图Fig. 10 Waveform of monitored radial seismic signal

对图10信号进行CEEMDAN·MPE-NHT时频分析。先对图10信号进行CEEMDAN·MPE,得到如图11所示的IMF分量。可发现,IMF从高频到低频排列,每个IMF都携带了爆破地震波信号的特定时频信息。其中IMF3携带图10所示信号的主要能量,其次是IMF4和IMF5。

图11 水平径向地震波信号CEEMDAN·MPE结果Fig. 11 The results of CEEMDAN·MPE of the radial seismic signal

进一步分析,对图11中的IMF1～IMF6执行NHT,获得每个IMF的时频能量特征图,其中图12～图17为对应IMF的边际谱;图18～图23为对应IMF的时频谱;这里未对IMF7和R进行变换,是因为结合图11不难发现IMF7和R占有的能量可忽略不计。观察图12～图23可发现,CEEMDAN·MPE-NHT获得的时频谱在时域和频域都具有高分辨率,这点和仿真信号时频分析得到的结果一致。IMF1的频率范围为100～250 Hz,持续时间为0.24～0.38 s;IMF2的频率范围为50～100 Hz,持续时间为0.23～0.42 s;IMF3的频率范围为20～50 Hz,持续时间为0.22～0.47 s;IMF4的频率范围为10～30 Hz,持续时间为0.28～1.17 s;IMF5的频率范围为5～10 Hz,持续时间为0.00～1.20 s;IMF6频率最低,约为0～5 Hz,持续时间为0.00～1.20 s。

图12 IMF1边际谱Fig. 12 Marginal spectrum of IMF1

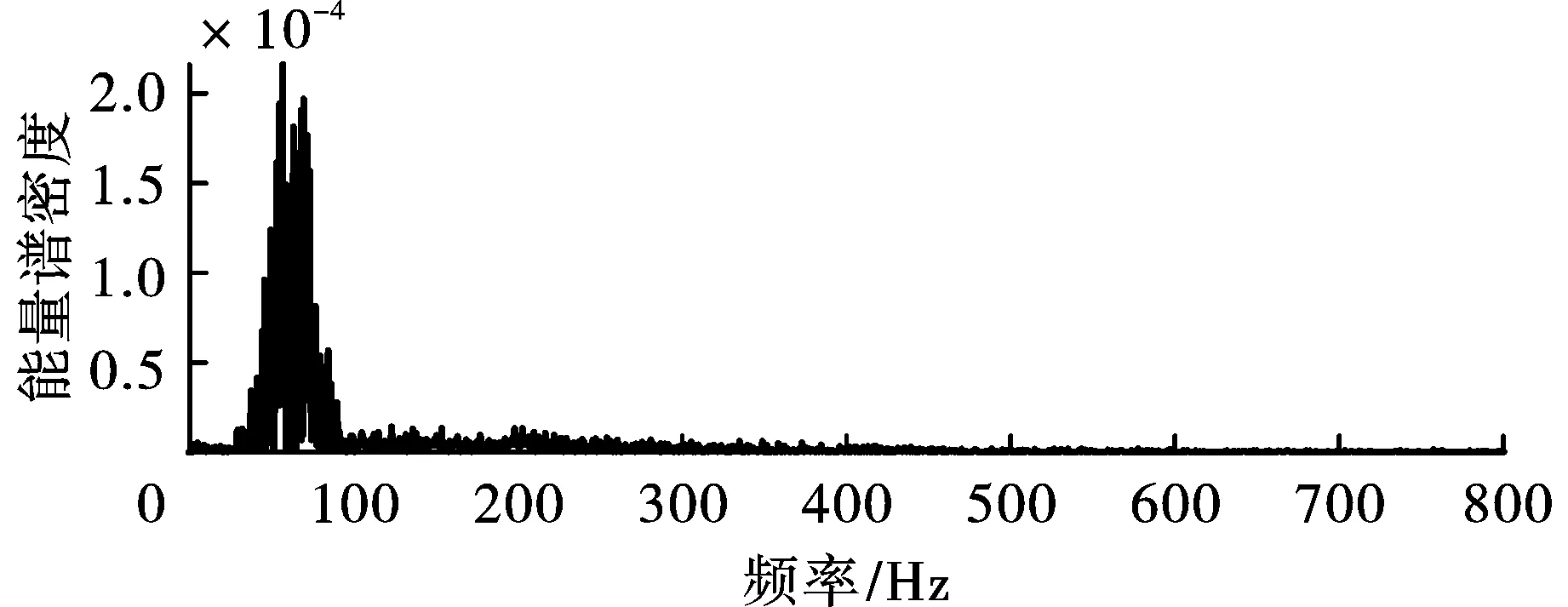
图13 IMF2边际谱Fig. 13 Marginal spectrum of IMF2

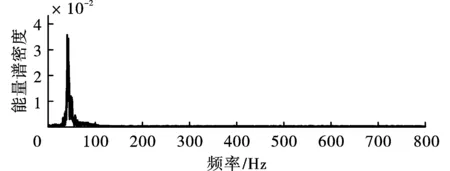
图14 IMF3边际谱Fig. 14 Marginal spectrum of IMF3

图15 IMF4边际谱Fig. 15 Marginal spectrum of IMF4

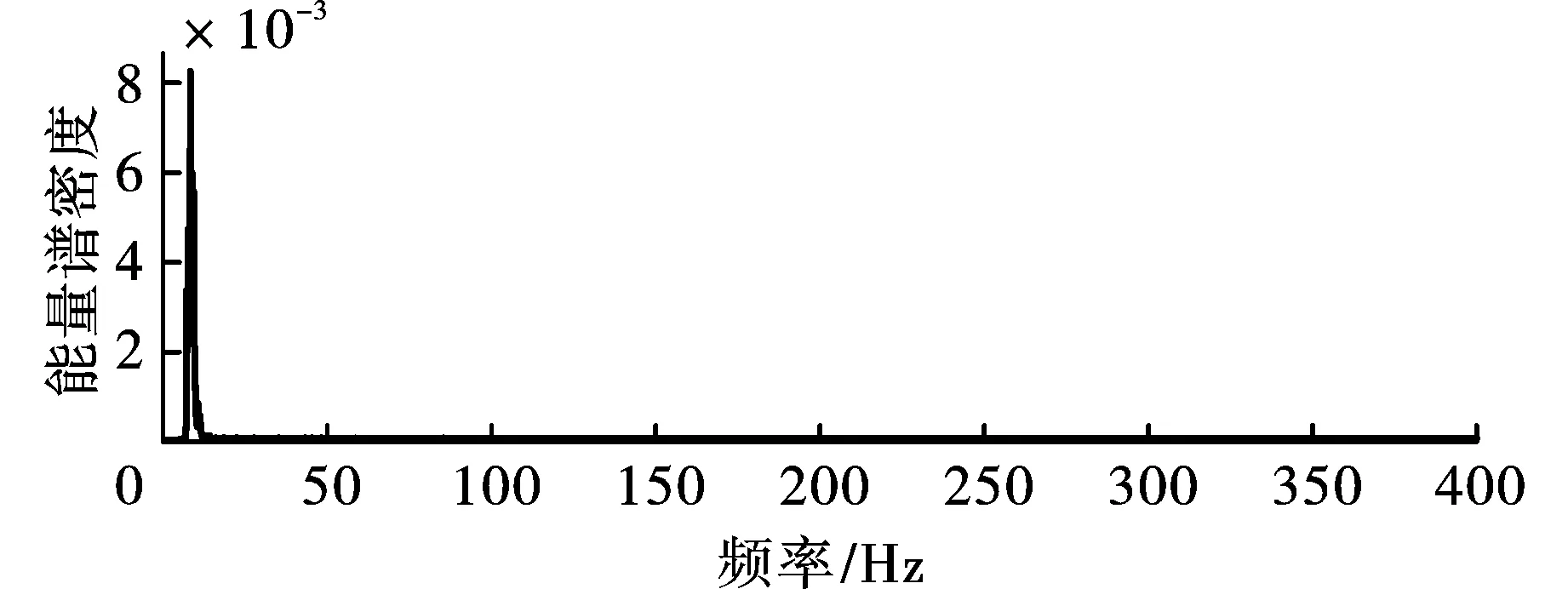
图16 IMF5边际谱Fig. 16 Marginal spectrum of IMF5

图17 IMF6边际谱Fig. 17 Marginal spectrum of IMF6

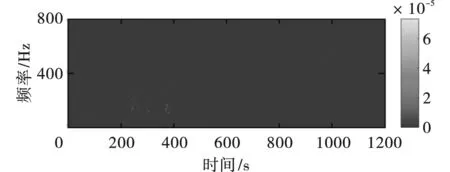
图18 IMF1时频谱Fig. 18 Time-frequency spectrum of IMF1

图19 IMF2时频谱Fig. 19 Time-frequency spectrum of IMF2

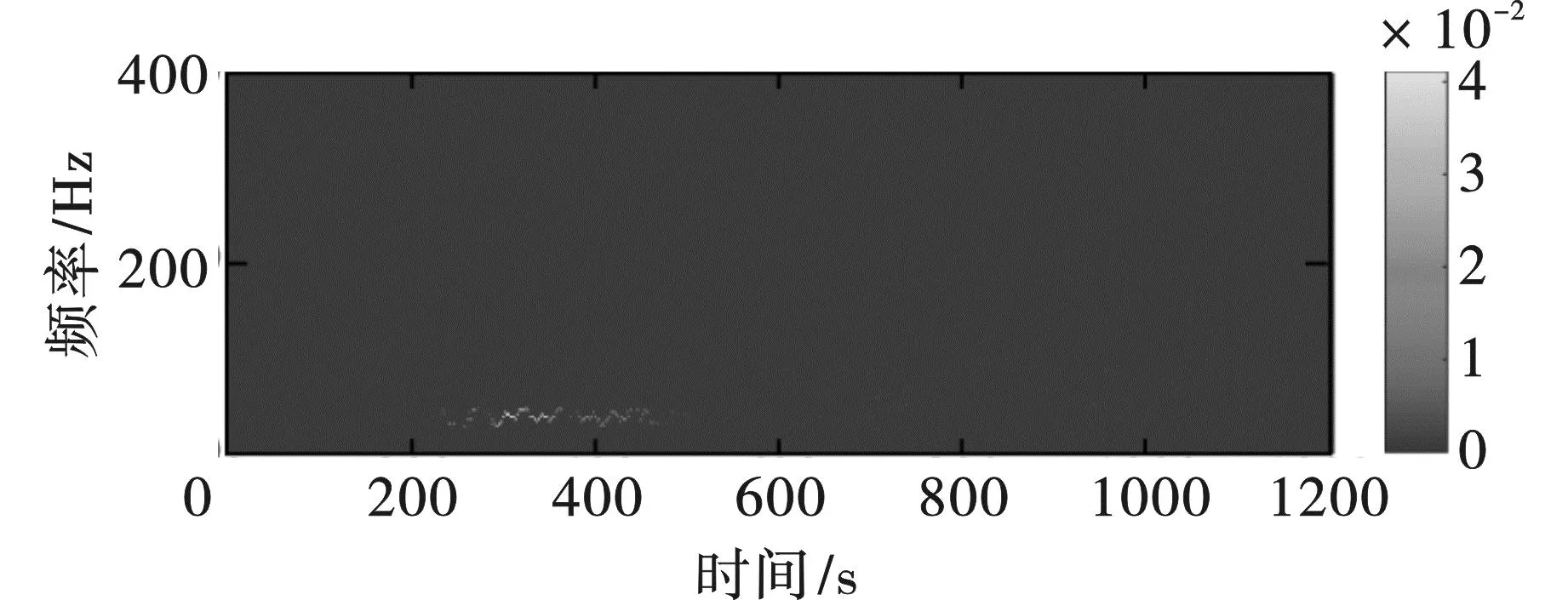
图20 IMF3时频谱Fig. 20 Time-frequency spectrum of IMF3

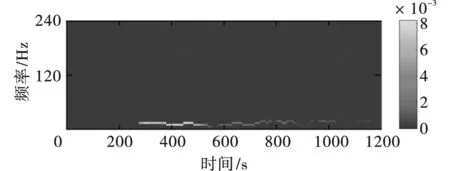
图21 IMF4时频谱Fig. 21 Time-frequency spectrum of IMF4

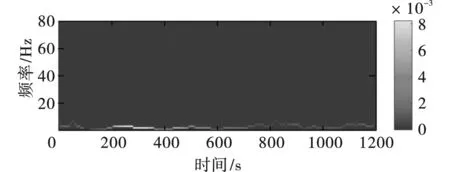
图22 IMF5时频谱Fig. 22 Time-frequency spectrum of IMF5

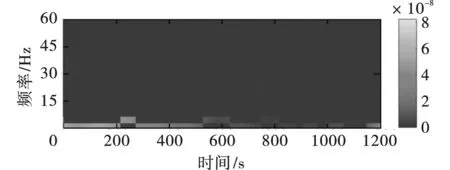
图23 IMF6时频谱Fig. 23 Time-frequency spectrum of IMF6

通过图12～图23的分析,可发现信号在低频停留时间大于高频,主要能量集中在50 Hz以下。

进一步分析,获得图10中信号的三维时频能量谱,如图24所示。从图24可看出,本次水下炸礁工程监测得到的水下钻孔爆破地震波信号的主频为26.83 Hz,次主频为19.32 Hz。

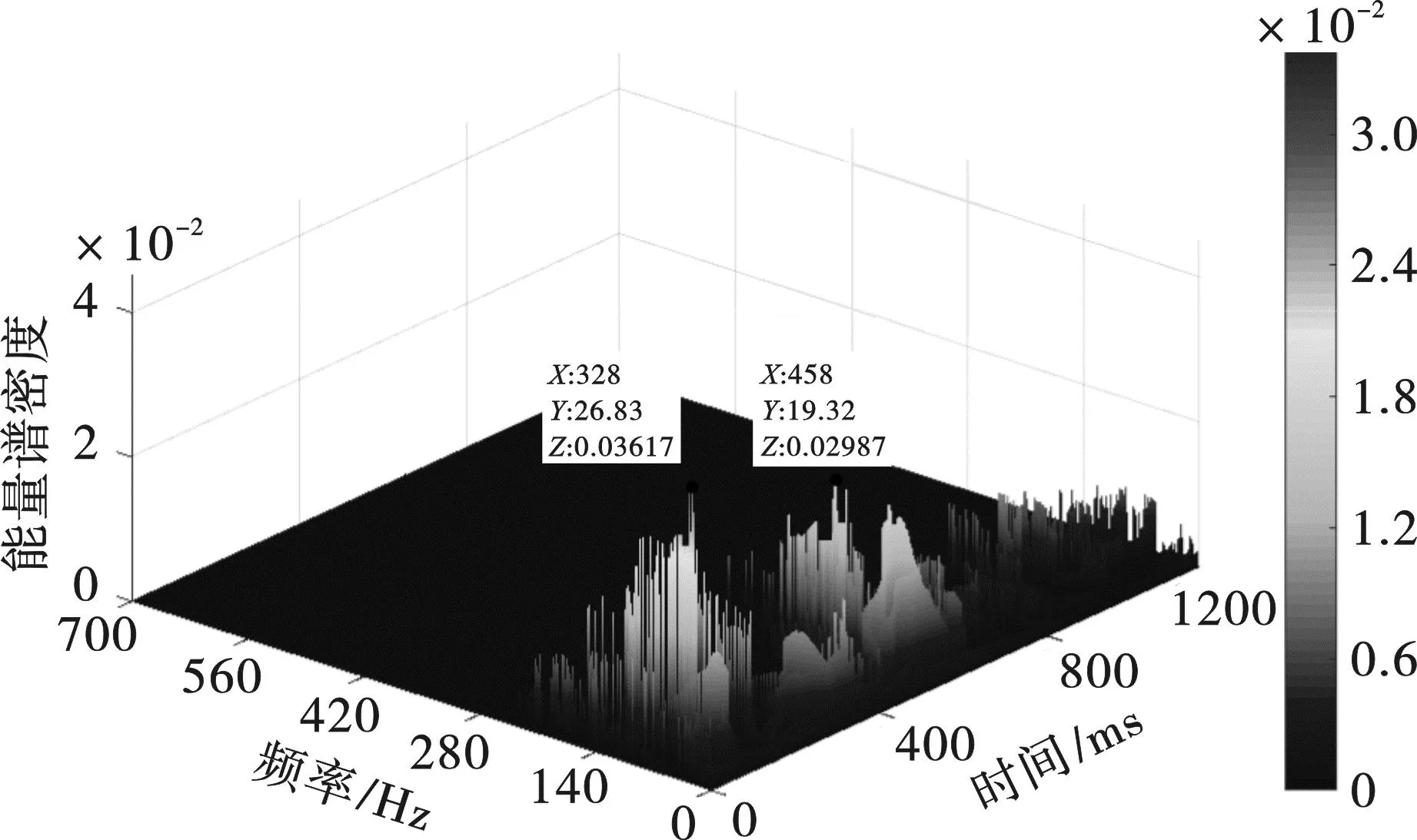
图24 信号时间-频率-能量三维图Fig. 24 Time-frequency-energy spectrum of the signal

根据结构抗震知识,当爆破地震波的频率与房屋的固有频率相同时,结构的振幅将达到最大,即发生共振危险。物体的受迫振动是根据特定规律进行的,即由于形状和结构的不同,它们具有不同的固有频率。为了探索建筑结构的固有频率,有必要分析结构的振动特性,如振动特征频率与频率对应的振型,即模态分析。通过PKPM结构软件的SETWE模块,对距离爆区最近的2层房屋进行了模态分析。房屋的第一个6阶振型图如图25所示,每个振型对应的固有频率如表1所示。

表1 民房前6阶阵型对应的自振频率(单位:Hz)Table 1 Natural frequency corresponding to the first 6-order array of civil houses(unit:Hz)

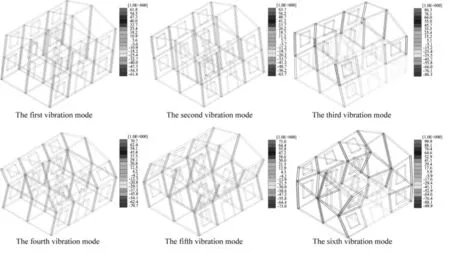
图25 民房前6阶阵型图Fig. 25 The first six formations of civilian houses

从表1中可看出,受保护房屋的第六阶阵型对应的自振频率为27.08 Hz,本次爆破的主频为26.83 Hz;被保护房屋的第五阶阵型对应的自振频率为20.17 Hz,本次爆破的次主频为19.32 Hz。根据结构共振的知识,不难发现此次爆破产生的地震波可能会引起该房屋的共振。

进一步定量分析不同IMF分量对民房每一阶阵型的影响程度,IMF对不同的建筑结构具有不同的放大倍数,根据式(1),可计算IMF分量对民房每一阶阵型的放大倍数,计算结果见表2,β为单个IMF主频和房屋各阶阵型固有频率之比,λ为阻尼比,一般建筑都λ取0.05。考虑到本次爆破地震波能量主要在IMF3中,其次在IMF4及IMF5中,所以仅对IMF3～IMF5对房屋不同阵型的放大性进行讨论。

表2 IMF分量对不同阵型下民房的放大系数DTable 2 The IMF component corresponds to the magnification factor D under different formations of civil houses

(1)

分析表2可发现,房屋固有频率和信号主频越接近即单个IMF主频和房屋各阶阵型固有频率之比β趋近于1时,D越大。D值大小反应在一定的外界爆破信号激励下,结构对应质点产生的质点振动速度放大效应,D值越大对应的爆破作用放大效应越强,对结构的损伤越大,结构发生破坏的概率越大。

不难发现IMF3可使民房第6阶阵型房屋质点速度产生9.9倍的放大效应。当IMF主频和阵型自振频率相等时,即β=1,此时D=10,结构振动幅度达到最大,这便解释了为什么民房处测得的速度峰值仅0.49 cm/s,但在民房处依旧产生了大量的裂缝,IMF分量对民房每一阶阵型的放大倍数是不一样的,实际结构在共振的作用下振幅呈现出放大的特征,可据此解释房屋在监测低振速环境下发生开裂的原因。因此,实际工作中安全评估不能以单一速度峰值作为判别标准。

继续观察表2还可发现,对于民房结构而言由于结构前六阶阵型相对较小,而高频信号对此种结构的影响相对50 Hz以下的低频影响相对小。针对此现象建议施工采用降低单段药量法、微差起爆、优化装药结构等提高爆破地震波信号频率的方法。

综上分析可发现,基于CEEMDAN·MPE-NHT的爆破地震波信号时频分析方法,不仅有助于抑制含噪监测信号引起的EMD模态混淆,同时CEEMDAN·MPE得到的IMF经NHT处理后,得到的时频谱在分辨率和精度上都得到了提升,分析结果有助于爆破振动特征的识别和爆破振动危害控制。

4 结论

(1)为提高HHT含噪爆破地震波信号时频分析精度,得到反映真实爆破振动属性的时频能量参数。对HHT进行了改进,得到CEEMDAN·MPE-NHT时频分析算法。该算法通过控制噪声来改善EMD模态混淆,对IMF调频分量进行Hilbert变换,降低负值瞬时频率出现的概率,从算法原理上实现提升信号时频分析精度。

(2) 通过HHT和CEEMDAN·MPE-NHT算法仿真爆破振动信号时频分析对比研究可发现,CEEMDAN·MPE-NHT算法将CEEMDAN的自适应性和MPE随机性检测能力相结合,降低EMD对噪声的敏感性。不仅可有效抑制噪声引起的EMD模态混淆,同时结合NHT可得到时频分辨率双高的信号频谱图。

(3) 根据结构共振放大系数D的原理,发现单个IMF分量主频和房屋不同阵型下固有频率越接近时,对应质点振动速度放大效应越明显。当出现极限情况,即当β=1,对应质点振动速度增幅可高达10倍。可据此解释房屋在低振速情况下,出现大量的爆破振动裂缝的情形。