基于OVMD-MPE算法的隧道爆破振动数据降噪分析*

王 双,赵文清,赵事成,郝广伟,龙福中,苏 晖

(1.山东省路桥集团有限公司,济南 250011;2.山东科技大学 山东省土木工程防灾减灾重点实验室,青岛 266590;3.山东大学 齐鲁交通学院,济南 250002)

爆破振动数据包括真实成分和无用噪声,直接对原始数据展开振动分析,噪声干扰现象明显[1]。在工程应用中通常认为,噪声信号多分布于信号的高频段中,而中低频段的平稳信号更多被认为是有用的真实信号。确定可靠性高的优势频段是进行信号分析的关键,有助于更早发现爆破施工中出现的质量问题,进行有效的爆破振动控制。因此,对采集的原始隧道爆破振动信号进行降噪预处理极为重要。

目前隧道爆破振动信号降噪方法主要包括阈值降噪、最小二乘拟合和模态分解三类。董鑫等将小波阈值降噪应用于滚刀主轴的振动信号分析中[2],有效消减了振动信号中的高频噪声成分;徐朗等采用最小二乘平滑滤波对光纤陀螺信号进行降噪[3],准确提取反映结构变形的特征信号;朱瑞金等和鲁铁定等依次将EEMD-MPE算法应用于发电功率分解和高程降噪领域[4,5],分解结果良好地反映出数据序列的非线性变化特性,王伯昕等将CEEMDAN-MPE算法应用于桥梁振动方向[6],取得了可观的去噪效果。

以上降噪方法虽然去噪效率进一步提高,但受限基础算法的局限性,很难摆脱由小波基选择造成的基础误差,以及模态分解中的混叠现象和端点效应。针对上述算法的局限,Dragomiretskiy等提出变分模态分解(VMD)方法,并在后续应用中有效消除了模态混叠问题[7,8],表现出良好的鲁棒性和运算效率。付文龙等提出了基于中心频率观察法与残差指标最小化准则确定分解参数的OVMD分解方法[9],有效弥补了VMD的局限,并成功应用于水电机组的振动分析。陈维兴等提出OVMD结合MPE的去噪算法[10],依据轴承监测数据进行故障分析,有效提高了轴承数据的故障准确率。爆破振动数据属于典型的非平稳随机数据,信号中噪声的种类和频率变化较大,对去噪算法的适配度提出更高要求。学界虽然对各类去噪算法展开了广泛应用,但尚未对实际隧道工程爆破背景下的OVMD等去噪算法进行优劣对比和适配度研究。

为此,首先采用仿真振动信号,对EEMD-MPE算法、CEEMDAN-MPE算法和OVMD-MPE算法开展对比分析,通过相关系数和MPE对分解得到的模态分量进行评价,验证三类算法的有效性和优劣度。然后,建立降噪误差比dnSNR、均方根误差ε和平滑度r的去噪评价体系。最后,依托双子山隧道工程掘进爆破实例,进行了实测爆破振动信号的去噪分析,确定适用于现场爆破环境的信号分解算法。

1 爆破振动降噪原理

1.1 OVMD原理

1.1.1 VMD原理

VMD算法是通过信号频域内的迭代计算,变换模态函数与中心频率,得到不同带宽的本征模态函数,具体步骤如下[11]:

(1)将原始信号x(t)分解为K个中心频率为ωk的模态函数uk,其中K为模态数,模态函数uk见式(1)。

uk(t)=Ak(t)cos[φk(t)]

(1)

式中:uk(t)为第k个分量;Ak(t)和φk(t)依次为瞬时幅值和相位。

(2)对uk(t)进行Hilbert变换,得到解析信号和单边频谱;解析信号加入中心频率,将模态频谱转换至基频带;计算解析信号梯度的平方范数,估计信号带宽,形成约束性变分问题求解IMF分量,约束性变分问题见式(2)。

(2)

式中:{uk}为K个IMF分量;{ωk}为分量对应的中心频率;δ(t)为脉冲函数。

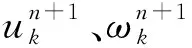
(3)

(4)

(5)

1.1.2 OVMD原理

OVMD算法是基于VMD算法的改进,不同于VMD分解中对于模态数K值和Lagrange乘子更新步长τ的盲目选定,OVMD算法通过中心频率观察法确定模态总数K,基于最小误差指数(REI)最小化确定更新步长τ,以期达到最好的VMD分解效果,REI公式见式(6)。

(6)

1.2 MPE原理

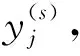
(7)

当s=1时,粗粒化序列为原始序列。

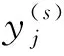
(8)

式中:l为第l个重构分量,l=1,2,…,N-(m-1)τ;m为嵌入维数;τ为延迟时间。

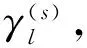
(9)

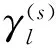
S(r)=(l1,l2,…,lm)

(10)

式中:r=1,2,…,R且R≤m!,嵌入维数为m的重构序列共有m!种排列;S(r)属于其中的一种排列。

(3)计算符号序列的概率Pr(r,1,2,…,R)后,用信息熵形式定义序列的排列熵Hp(m),排列熵Hp(m)公式见式(11)。

(11)

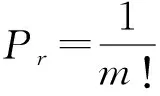
(4)对Hp(m)进行归一化处理得到Hp

(12)

式中,Hp为归一化处理的排列熵值,熵值越小则时间序列越平整。多尺度排列熵反映信号的随机程度,对于隧道爆破施工振动信号[12],MPE阈值通常取0.6。

2 爆破振动仿真信号分析

振动信号的去噪效果多与信号质量和算法的适配度有关,高质量的信号对于检验去噪算法的性能意义重要,但实测信号通常周期较短、细部特征相对微小,较难对去噪效果起到明显的检验效果,通过既定的合成信号进行仿真分析,有利于保证信号质量,补充算法性能检验的空白,提高振动分析的可信度。

2.1 建立仿真信号

爆破信号的采集通常与渣土运输、钻孔排风等工序同步进行,采集到的爆破信号受多类高频噪声的影响。构造多频信号叠加的仿真信号[13],有助于论证算法在高噪声、多频段情况下的准确性,仿真信号表达式如下

(13)

式中,ψ(t)为高斯白噪声。VMD算法中分解完备性平衡参数取默认值2000,仿真信号时域波形如图1所示。从图1可以看出,仿真信号设置合理,与工程实际情况较为接近。

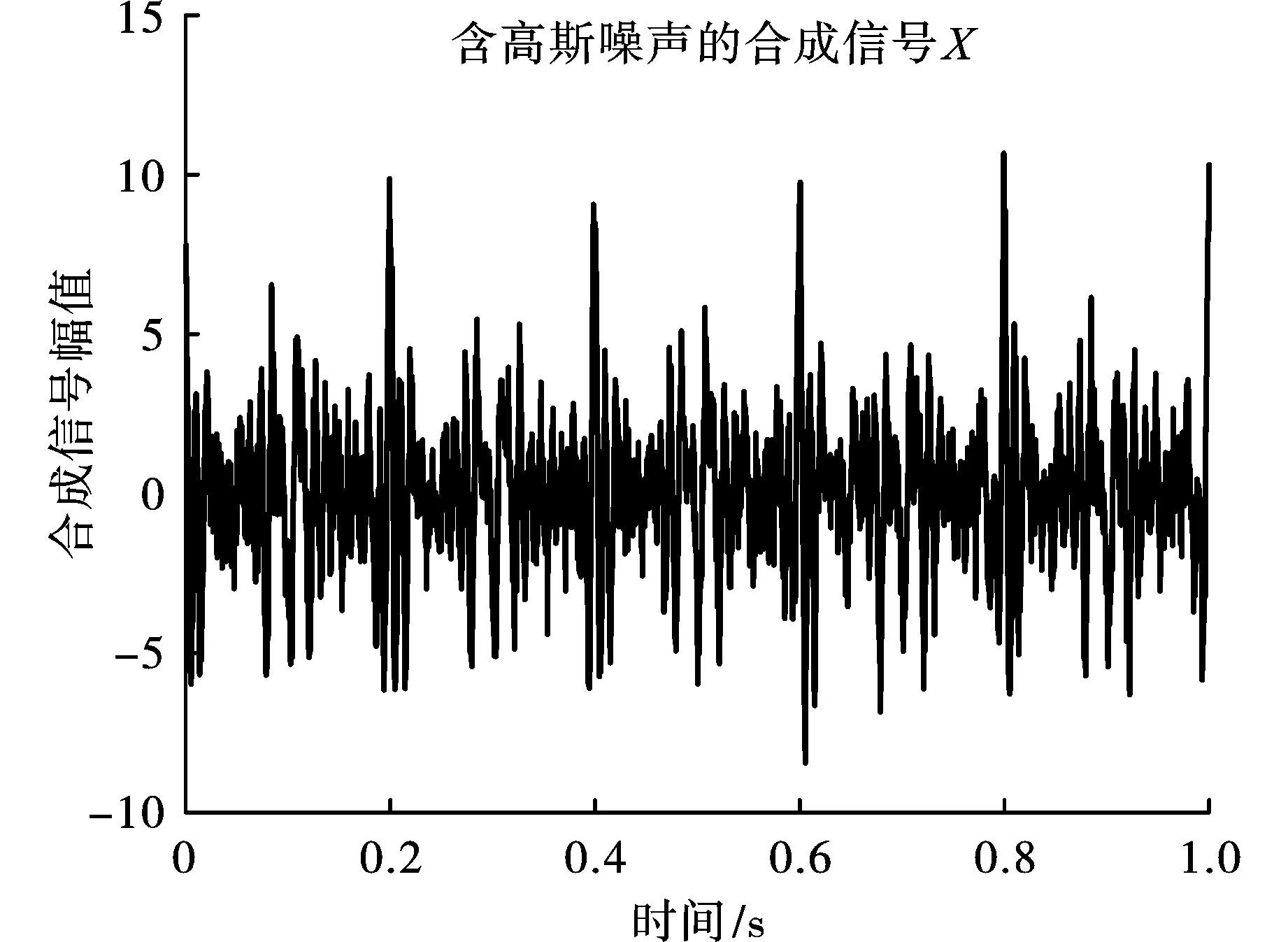
图1 多频合成信号时域图Fig. 1 Time domain diagram of multi-frequency synthetic signal

2.2 算法优劣分析

为更好比较三类算法的优劣,对仿真信号依次进行EEMD-MPE、CEEMDAN-MPE和OVMD-MPE分解,各阶IMF分量与仿真信号的相关系数和MPE值见图2所示。由图2(a)可知,相关系数整体呈先增加后降低的趋势,结合三类算法分解过程的差异,可以看出OVMD算法在前两阶分量中有效分解出原始信号的核心部分,而CEEMDAN、EEMD算法的IMF3～IMF5为分解信号的有效信号部分。参考图2(b)可知,OVMD算法的相关性和MPE值成强负相关关系,即OVMD的IMF1、IMF2分量在相关系数和多尺度排列熵方面表现一致,有良好的互相关性。而CEEMDAN、EEMD算法的IMF1～IMF5与原始信号相关性较高,结合MPE数值可以发现,IMF1～IMF3可认为是噪声部分,即CEEMDAN、EEMD算法的IMF分量存在部分误差,较难有效区分噪声部分。

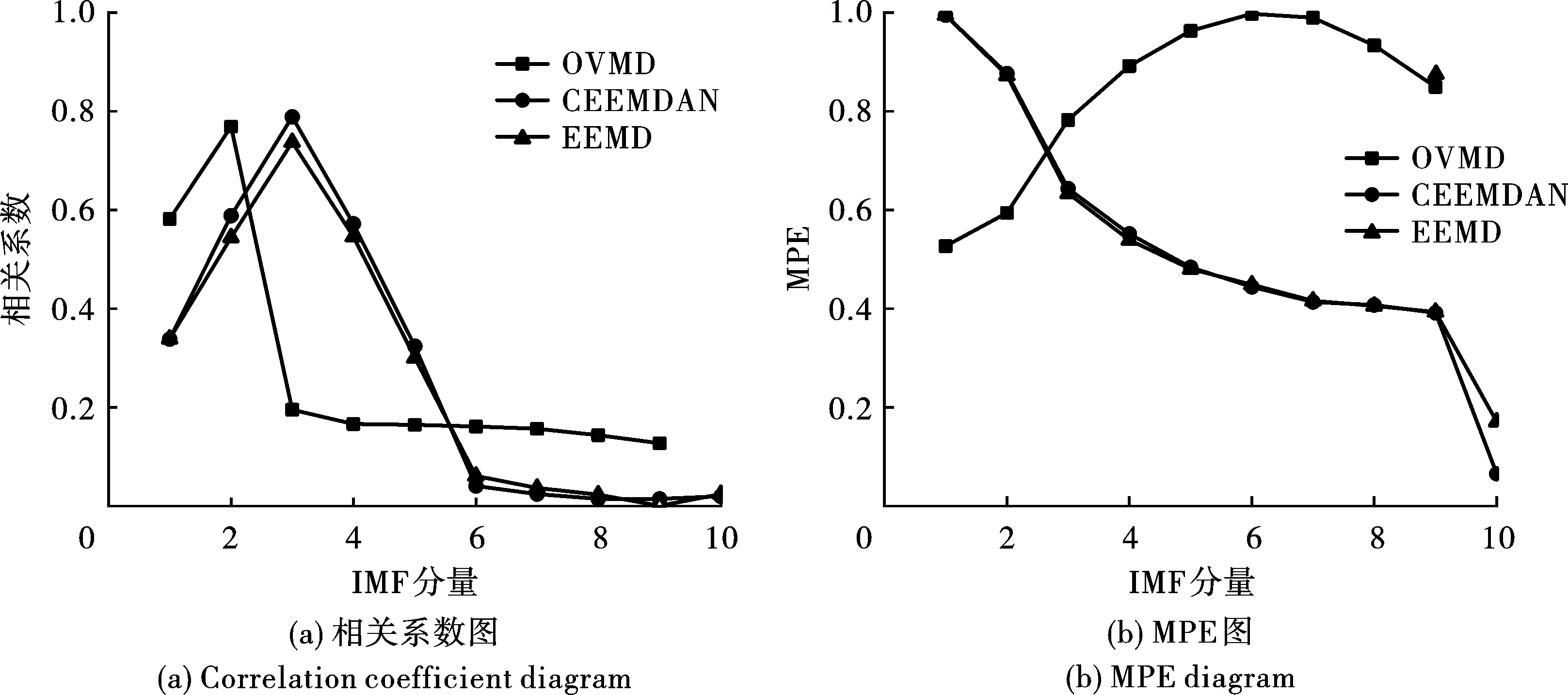
图2 IMF分量相关系数和MPE图Fig. 2 Correlation coefficient and MPE of IMF component

考虑到OVMD算法的交替迭代分解与EMD及改进算法的分解过程有较大不同,对仿真信号经OVMD分解的结果进行分析,得到的若干个IMF及余项见图3。观察图3可知,OVMD对多频合成仿真信号进行了有效分解,各分量中心频率独立,受噪声影响时域波形差异明显。IMF1～IMF6的中心频率逐渐增加,可发现IMF1～IMF3反映了多频叠加信号的主要波形,而IMF4～IMF9则部分受到高斯噪声影响。

图3 OVMD分解图Fig. 3 Decomposition of OVMD

3 工程实例分析

3.1 工程背景

试验以潍坊市青州市的双子山隧道为背景,隧道左线长2015.0 m,隧道右线长2057.0 m,海拔高程为275.1～474.5 m,相对高差约199.4 m,隧道最大埋深约157.7 m。隧道围岩以Ⅲ级和Ⅳ级为主,占比为31.56%和44.95%。隧道围岩饱和单轴抗压强度集中于25.6～29.2 MPa,占比为44.53%。隧址区主要岩性为古生界寒武系页岩、灰岩夹泥灰岩薄层。

双子山隧道位于北镇头村西南侧约1200 m处,工程现场炮孔直径42 mm,采用2号乳化炸药进行CD法和上下台阶法爆破施工。采用TC-4850N爆破振动监测仪展开振动监测,测点等距600 m进行布设,共设置6个测点,测点最远至北镇头村村庄房屋处。开展监测过程中,双子山隧道处于入口段施工,施工里程段为ZB1K96+700～ZB1K96+721,围岩条件主要为中风化灰岩加页岩薄层,岩石单轴饱和抗压强度为12.8～18.6 MPa。见图4。

图4 隧道测点布置图Fig. 4 Tunnel measuring point layout

3.2 降噪效果评价指标

由于实测信号的有效信号和噪声功率未知,采用常规信噪比等评价指标评价降噪效果的准确度较低,因此引入降噪误差比dnSNR、均方根误差ε和平滑度r结合作为降噪质量评价指标[14,15]。

(1)降噪误差比dnSNR

降噪误差比dnSNR是基于常规信噪比的改进指标,多适用于有效信号和噪声功率未知的实测信号。一般认为,dnSNR值越小降噪效果越显著。

dnSNR=10 lg(Ps/Pg)

(14)

式中:Ps为含噪信号的功率;Pg为滤波的噪声功率。

(2)均根方误差ε

均根方误差ε主要用于评价去噪信号和真实信号的误差,体现了降噪后信号与原始信号的相似程度,通常ε越小降噪效果越显著。

(15)

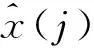
(3)光滑度r

当去噪效果很小时,虽然以上两个指标结果符合要求,但未达到去噪的目的,不能反映出去噪的效果。考虑到此类问题,引入光滑度r进行去噪效果评价,进而有效反映去噪信号的平滑程度。

(16)

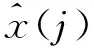
3.3 降噪效果评价

为充分检验去噪算法的效果,考虑爆破振动的衰减效应。选用全部6个测点进行降噪效果评价,爆破振动数据依据双子山隧道右线的爆破振动监测,监测点具体参数见表1。通过观察表1可知,在多点测振过程中,X方向的振速整体处于较高范围,主振频率更高,因此取上述6个测点的X方向信号分量展开分析。

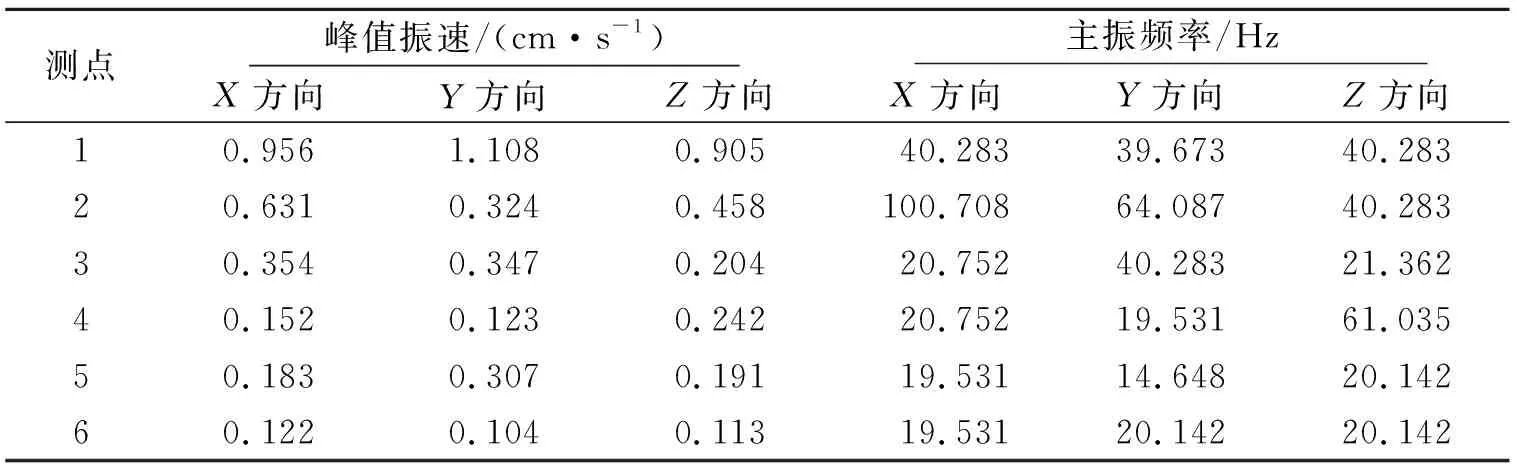
表1 不同测点的爆破参数Table 1 Blasting parameters of different measuring points

对选定分量进行EEMD-MPE、CEEMDAN-MPE和OVMD-MPE分解,计算相关降噪效果指标,具体数值见表2。通过观察表2可知,针对距震源不同距离的测点,EEMD-MPE和CEEMDAN-MPE的整体算法性能相近,而OVMD-MPE算法性能更为优异,降噪误差比更高,有效保留了原始信号的有用部分,而均根方误差和光滑度更低,去噪后的曲线更贴近原始信号,避免了有用信号的无序剔除。为充分体现三类算法的具体差异,选取测点2#的X方向信号,将原始信号与三类去噪信号置于同一时间序列进行对比,具体见图5。通过图5可发现,OVMD-MPE去噪后的信号有效剔除了部分高峰值噪声信号,去噪后的信号与原始信号的主体部分更为贴合清晰。

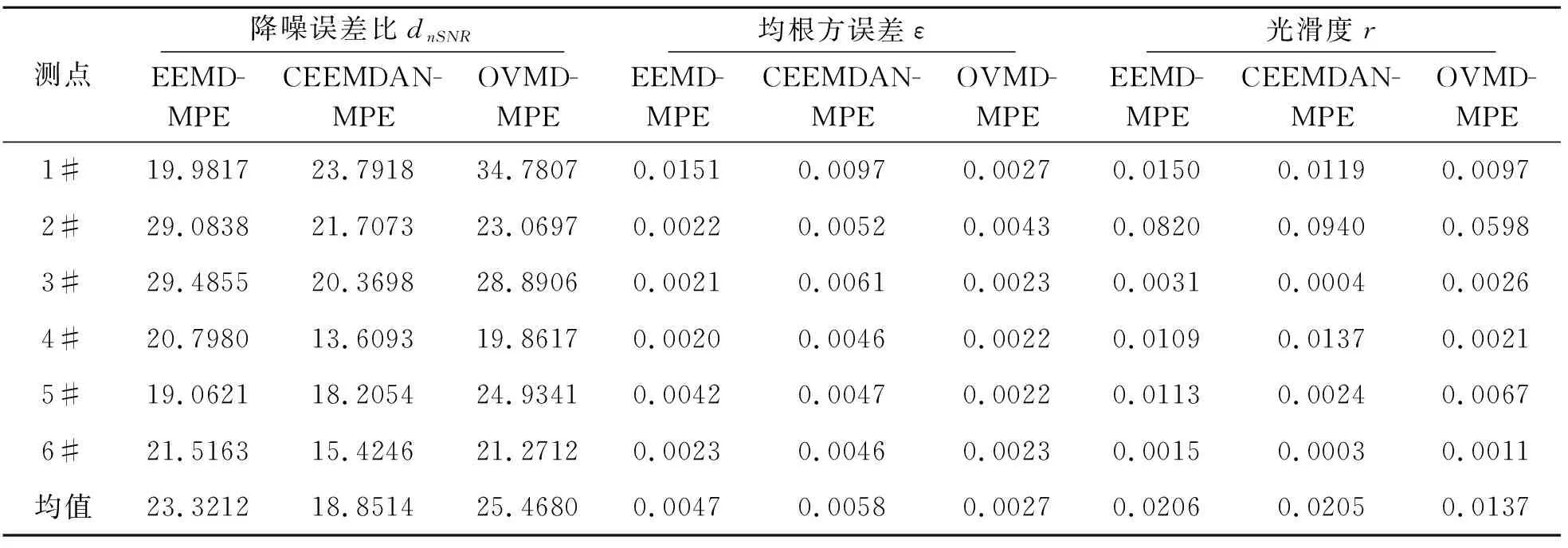
表2 降噪效果评价参数表Table 2 Parameter table for noise reduction effect evaluation

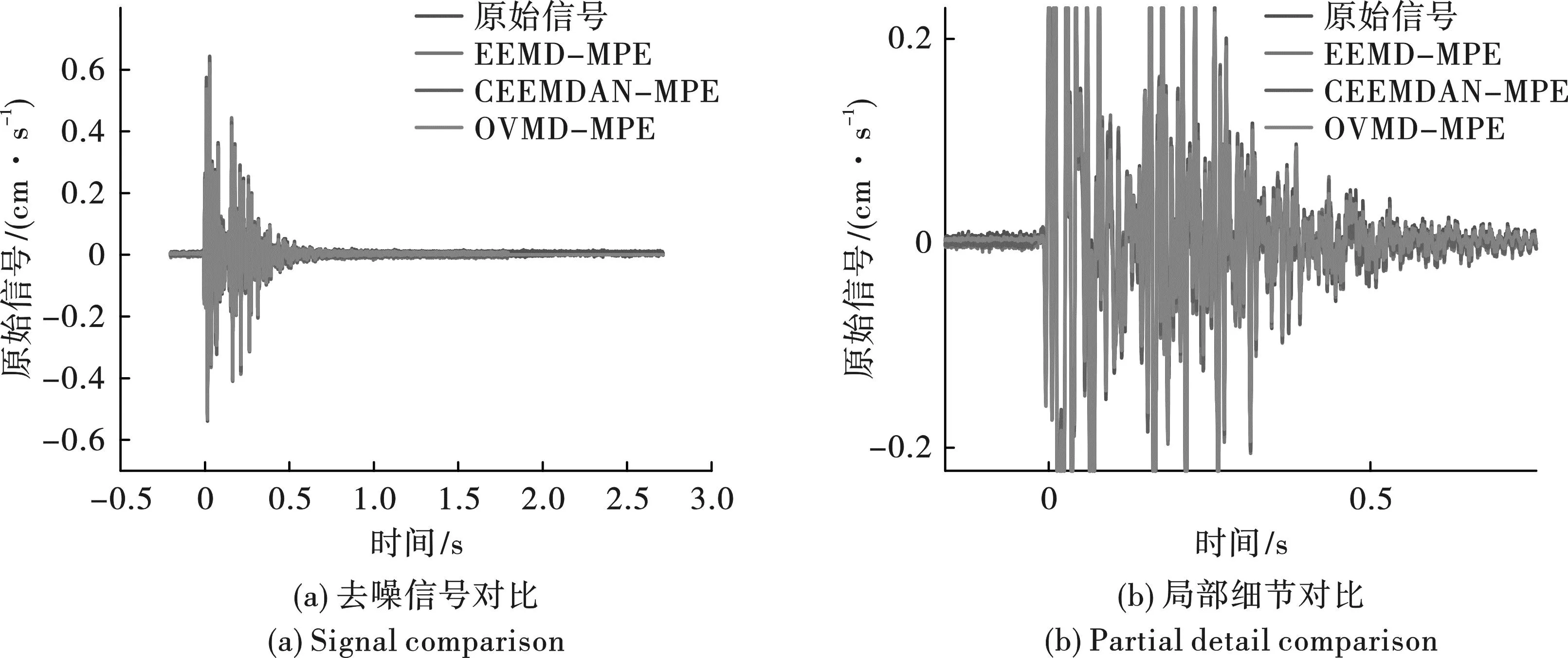
图5 EEMD-MPE、CEEMDAN-MPE和OVMD-MPE的去噪信号对比Fig. 5 Comparison with denoising signals of EEMD-MPE,CEEMDAN-MPE and OVMD-MPE

3.4 时频能量分析

为充分反映双子山隧道右线施工对隧道内部建构筑物和左线既有工程造成的扰动,选取1#、2#的振动数据进行时频能量分析,具体见图6。结合图6(b)可发现,2#的频谱主要分为两部分,少量为400～550 Hz的中高频信号,大部分为10～220 Hz的中低频信号,未出现大于600 Hz的超高频信号。因此,可认为OVMD-MPE处理后的去噪信号有效地降低了高频噪声的扰动。同时参考图6(a)的关于1#的时频谱图,可发现信号的频段集中于200 Hz以下的中低频段,考虑到爆破地震波达到1#测点需经过左线既有隧道,信号可能出现一定程度的衰减,与图6(b)的情况吻合。参考既有安全规程[16],可发现双子山隧道爆破产生的地震波的主振频段与既有隧道工程中的衬砌等工程部件的频段重合,可能对既有隧道的施工安全产生扰动,可采取优化孔眼深度、改善孔底间距、减震排孔、增大底部空气间隔、调整自由面等方式[17],以降低爆破振动对隧道结构的影响,确保整体工程的施工安全。

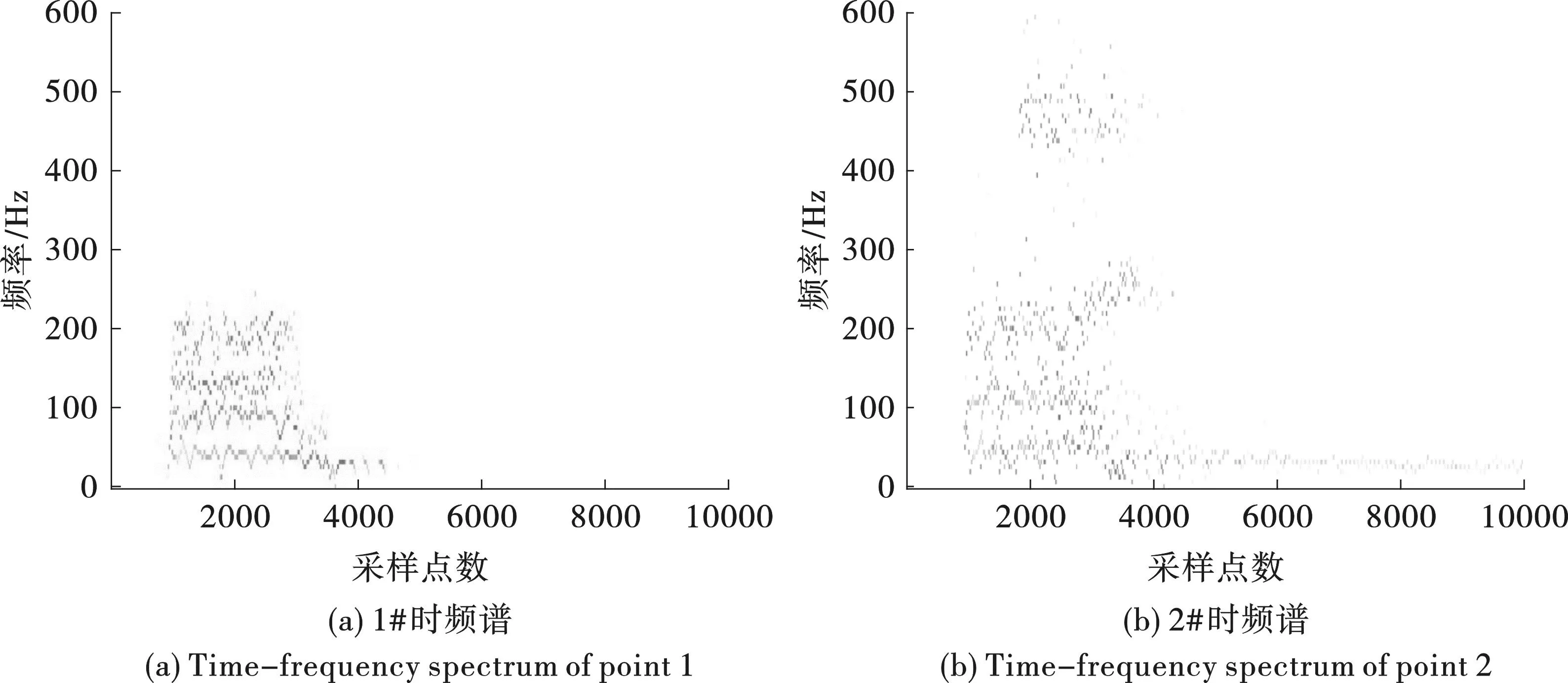
图6 双子山隧道1#、2#时频谱图Fig. 6 Time-frequency spectra of Shuangzishan Tunnel 1# and 2#

4 结论

(1)对于多频叠加振动信号而言,OVMD-MPE算法能准确识别多频信号中的频率信息,且分解得到的前两阶分量能良好反映叠加信号的有效成分,具有较好的时频能量聚集特性和抗噪性能,可适用于高精度的振动信号序列分析。

(2)依据双子山隧道的实测爆破振动信号,选择距爆源不同距离的测点振动数据进行降噪分析,与 EEMD-MPE、CEEMDAN-MPE算法相比较,OVMD-MPE算法具备更好的准确性,表现为:去噪后信号整体的降噪误差比、均根方误差和光滑度平均提升22.05%、48%和33.34%,降噪性能显著提高。

(3)根据实测振动信号去噪后的频谱能量分析,信号的频段主要分布于200 Hz以下,与隧道衬砌结构的共振频段重合,施工隧道的爆破可能对既有工程产生较大的扰动,需要进行有效的抗震减震措施,确保工程的整体施工安全。