引水工程水下钻孔爆破水击波特性*

刘屹颀,蔡子勇,2,乔世范,余鹏鲲

(1.中南大学 土木工程学院,长沙 410075; 2.中湘海外建设发展有限公司,长沙 410004)

水下钻孔爆破炸药爆炸荷载作用,在水介质中产生的冲击波能量远远大于在岩体介质中应力波能量,极可能对水体及临近建(构)筑物的稳定性造成不利影响[1]。因此,关于水下爆破爆炸波在水域中传播所带来的危害效应问题一直是爆破工程领域研究的重点。

针对水下爆破水击波传播特性,Cole介绍了水下爆炸现象、荷载传播及分布特点[2],提出了水击波峰值压力及衰减计算公式。吴志刚[3]、王亚鹏等基于水下爆破现场试验[4],分别阐明了球形和柱状药包爆炸后水击波传播衰减规律,反映了其影响效果的不同。此外,Liu等[5]、Wang等[6]、彭亚雄等通过水下爆破现场实测数据[7],研究了水击波的传播特性及其峰值压力随爆心距的衰减特征。然而,由于水下钻孔爆破爆炸荷载作用下水击波的形成与传播是一个相当复杂的不可逆过程,现场监测和理论研究具有一定局限性。于是,人们开始借助数值分析软件对水下钻爆作用机理及传播规律深入研究,通过从炸药成分[8]、炸药包形状[9,10]、水深[11,12]、爆破延期时间[11]、钻孔堵塞长度[12]、起爆方式等方面揭示了不同工况下的水击波的传播规律、爆破效果及其水击波动力响应机制[13,14],研究成果丰富了爆破振动在水体中的传播理论。

总的来说,目前国内外学者对水下爆破水击波特性研究主要集中在水下炸礁、水下岩塞及水下围堰拆除等爆破工程,对于引水工程水下钻孔爆破案例研究相对较少。同时考虑炸药爆炸能量传递、冲击波的传播介质以及边界域等影响,模拟水下爆破水击波的传播有一定的难度,特别是目前常用的ANSYS/LS-DYNA软件分析过程中假定岩-水接触面为无反射边界,与实际情况有所差异。因此,本文以桂林市第二水源工程-引水工程子项青狮潭水库取水工程为背景,通过COMSOL多物理场耦合模拟方法,采用任意拉格朗日-欧拉(ALE)技术处理流体区域的网格以及设置人工低反射边界,在固体力学系统添加瑞利阻尼模拟土体对爆破荷载的阻尼作用,建立水下钻孔爆破数值分析瞬态求解模型,研究钻孔爆破爆炸荷载作用下水击波传播特性,并结合现场监测进行评价,研究成果可为类似工程经验积累及其安全预防提供指导和借鉴。

1 工程概况

依托桂林市第二水源工程-引水工程子项青狮潭水库取水工程,其包含取水口、引水隧洞建设工程(见图1)。取水口按照70万 m3/d设计,引水工程完工后运营期可分别单独向桂林市西城水厂、城北水厂供水40万 m3/d,也可同时执行两个水厂的应急供水任务,是桂林市近年来开工建设的重大民生项目之一,也是周恩来总理亲自审定的国家级大型水库。引水隧洞工程起点为青狮潭水库大坝右岸溢洪道侧山体附近的进水口竖井,沿山脊线向东南方向布置,终点为青狮潭镇青狮潭社区南侧附近山体出洞,引水隧洞全长1.0 km,取水工程主要涉及上、下层取水口水下钻孔爆破和竖井基坑开挖爆破工程,区域工程地质主要地层分布为:①第四系全新统人工填土层(Q4ml);②第四系残坡积(Q3el+dl)黏性土层(粉质黏土、含角砾粉质黏土);③泥盆系中统信都组(D2x)泥质砂岩、砂岩等地层。

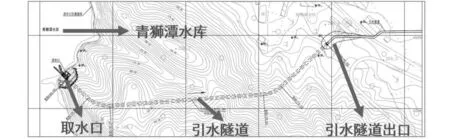
图1 引水工程平面图Fig. 1 Water diversion project planar graph

2 水下钻孔爆破数值分析

2.1 模型建立

通过采用COMSOL软件对水下钻孔爆破进行数值模拟,模型参数及边界条件选取:①模拟水库库水深度取施工期实际水深22 m;②水下钻孔的形状采用多孔圆柱体;③模型的所有截断边界均设置低反射边界条件以模拟无限边界的岩体和大面积水域,与空气接触的表面选择自由边界;④忽略水流速度与空气对水下爆破的影响;⑤不考虑冲击覆盖物的影响;⑥假设爆炸压力在炮孔沿孔壁均匀分布;⑦为消除边界效应,取模型尺寸的长×宽×高=473 m×161 m×91 m。网格划分采用自由四面体网格,单元大小选择超细化进行建模。计算模型网格单元数为101206个,水下钻孔爆破计算模型如图2所示。

图2 水下钻孔爆破计算模型(单位:m)Fig. 2 Calculation model of underwater drilling and blasting(unit:m)

2.2 材料模型及参数

根据物探报告,模型计算区域的岩性主要是泥质砂岩,实际大坝为夯土(内部为C30混凝土芯墙),在进行模型建模时,考虑工程实际情况,选择合适的力学参数来模拟实际工程中的岩石、土层等。各种材料的属性如下表1所示。

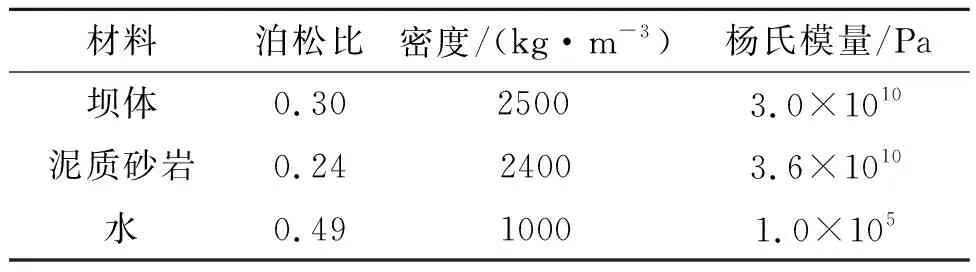
表1 模型材料参数取值Table 1 Values of model material parameters

同时,建立适当的爆破荷载施加模型是研究建(构)筑物动力响应规律的关键。在爆炸过程中,岩体首先受到来自炸药爆炸急剧上升的压应力,随后压应力快速衰减至零,最后由于温度下降产生负压力。为此,选择在炮孔壁上施加半理论半经验的爆破荷载压力曲线,具体如图3所示。

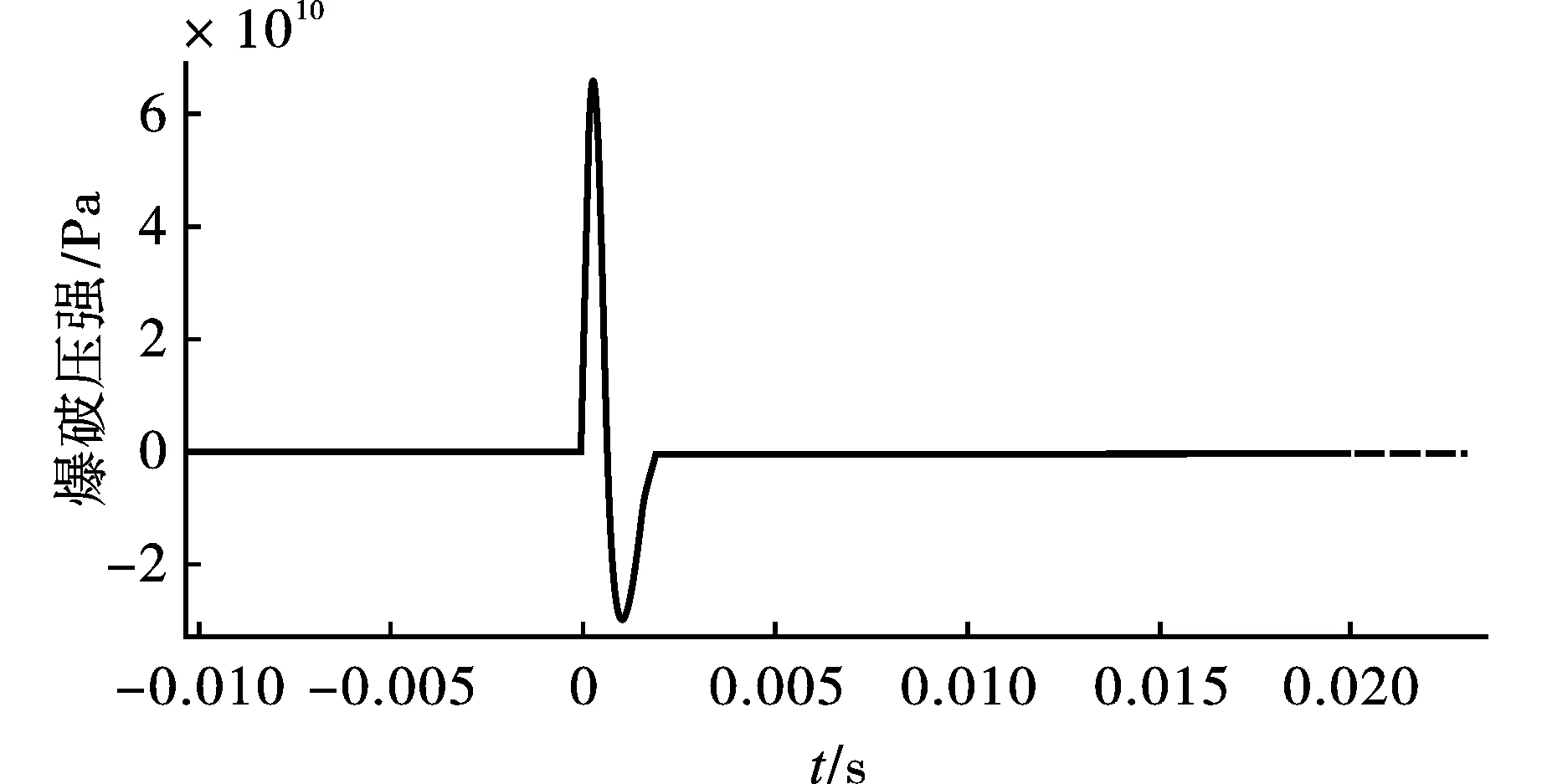
图3 爆破荷载时程曲线Fig. 3 Time history curve of blasting load

此外,在水下钻孔爆破分析模型中,由于炮孔数较少,全部布置为主爆孔,由软件自动控制时间步,从0 s开始,在爆破荷载的加载时间内,每0.0001 s记录一次求解结果,其他时程中每隔0.001 s记录一次求解结果。考虑爆破施工装药量和爆孔深度密切有关,每次爆破装药量不同,单孔装药量按照孔深2/3控制,实际工程中,为了充分利用炸药能量,设置孔网参数为1.8 m×1.4 m,按矩形布置2排炮孔,采用分段延时(25 ms)控制爆破技术进行一次起爆方式,模型中炮孔起爆位置设置为药卷底部,水下钻孔爆破装药参数如表2所示。

表2 水下钻孔爆破装药参数Table 2 Charging parameters of underwater blasting

2.3 模拟工况

为研究水下钻孔爆破的水击波传播衰减规律,在数值分析计算模型上布置5个水击波测试监测点,水击波监测点位置在模型中的坐标依次为:监测点1(50,203,25)、监测点2(50,183,25)、监测点3(50,163,25)、监测点4(50,143,25)、监测点5(50,123,25),其距水下钻孔爆破点位的距离分别为28 m、48 m、68 m、88 m、108 m,如图4所示。

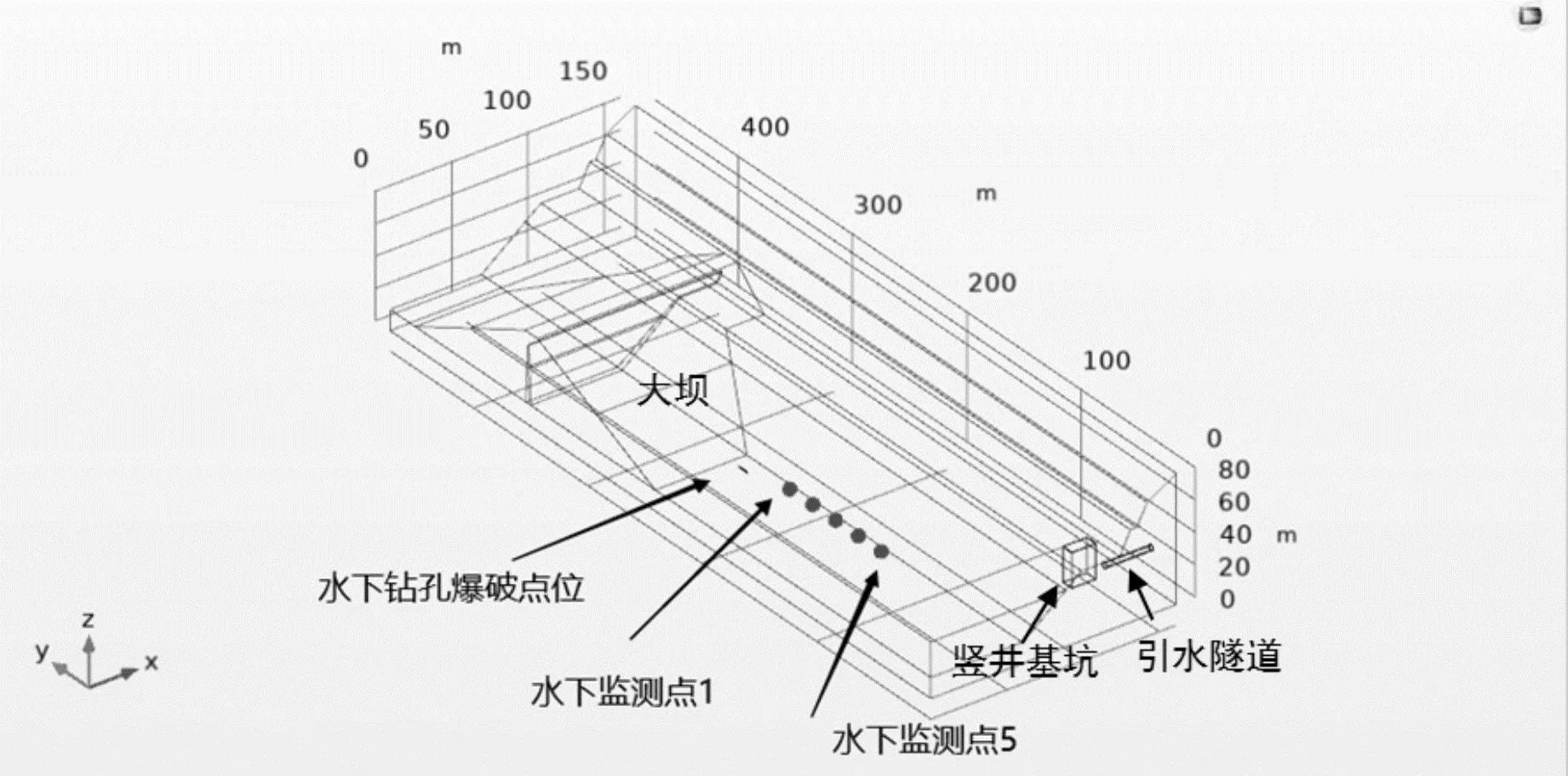
图4 数值模型监测点布置(单位:m)Fig. 4 Layout of monitoring points of numerical model(unit:m)

2.4 模拟结果分析

2.4.1 不同时刻水击波等值面云图

设置水击波波速v=0.0001 cm/s,模拟得到t=0.0001 s、t=0.001 s、t=0.003 s时刻的水中水击波等值面云图如图5所示。

图5 不同时刻水击波等值面云图Fig. 5 Contour nephogram of surge wave at different times

从图5可以看出,水下钻孔爆破起爆后,水击波随时间推移由爆破点逐渐向四周传播,引起距爆源不同距离区域内的水体介质速度发生变化,与曲艳东等研究结论一致[15]。在t=0.0001 s时形成较完整的水击波波阵面,水击波速度形态较为规则,近似球型,主要原因是考虑孔壁均匀施加爆炸荷载,钻孔内的炸药爆炸产生冲击波,迅速从孔口位置向水介质中传播;当t=0.001 s时,水击波波阵面不断扩大,由于岩-水交界面反射与折射等作用,水击波速度分布开始出现不规则椭球形状;当t=0.003 s时,水击波等值面分布复杂程度更高,特别是距离孔口较远区域。由于炮孔内产生的冲击波与自由水面反射波联合作用,水域中形成反射稀疏波。

2.4.2 爆破结束时刻不同水击波波速等值面云图

设置爆破结束时刻t=0.0019 s,模拟得到v=0.1 cm/s、v=0.01 cm/s、v=0.001 cm/s、v=0.0001 cm/s、v=0.00001 cm/s时刻水下钻孔爆破点(见图4)的水击波等值面云图如图6所示。

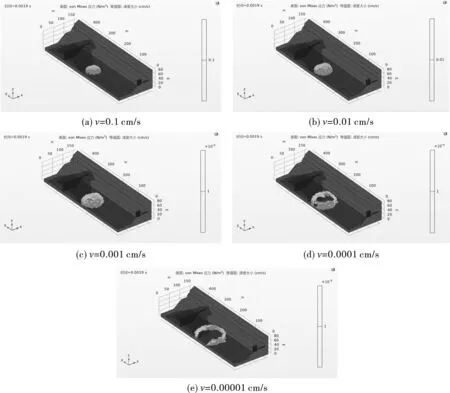
图6 爆破结束时刻不同水击波速度等值面云图Fig. 6 Contour nephogram of different surge wave velocities at the end of blasting

从图6可以看出,爆破作用结束之后,水击波在水中传播过程中衰减很快,时效性显著。随着水介质速度阈值增大,爆破作用所产生的水击波作用区域迅速减小,当水介质速度值为1×10-5cm/s时,爆破冲击波的作用区域勉强到达坝底位置。

2.4.3 不同监测点处水击波的应力时程曲线

提取水下不同钻孔爆破监测点处水击波有效应力,得到其随爆心距的衰减曲线如图7所示。

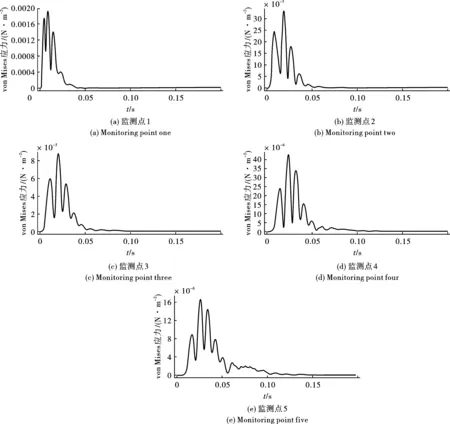
图7 不同监测点处水击波应力时程曲线Fig. 7 Stress time history curve of surge wave at different monitoring points

从图7可以看出,每个监测点的应力时程曲线均存在多个波峰,主要原因是本模型中的水下钻孔爆破采用的是毫秒延时爆破,孔间起爆延时为25 ms,由于装药不同部位起爆的时间差,导致水下爆炸荷载作用水击波传播在不同位置出现叠加效应,这意味着各个监测点的水击波峰值应力不一定是由某段爆破引起的,而是多段爆破的叠加效应产生的结果。

从图8可以看出,随着监测点爆心距增加,水击波峰值应力呈先加速下降后缓慢下降趋势,受到的钻孔爆破影响逐渐减小。对不同监测点的峰值应力进行曲线拟合,得到指数函数y=0.0208e-0.04855x,相关系数R2=0.9986,具有较强的相关性,水击波的峰值应力传播符合指数形式衰减规律,王亚鹏等佐证了这一观点[4],进一步说明了此次数值模拟的合理性,可以利用该曲线预测不同爆心距对应测点位置的水击波峰值应力。同时,随着爆心距的增加,水击波峰值应力降低的速率也呈指数下降,在爆心距较小时,水击波峰值应力下降速度明显,当爆心距达到68 m时,水击波峰值应力下降变得很小,可以基本忽略。

图8 不同监测点水击波峰值应力随爆心距变化曲线Fig. 8 Curve of peak stress of surge wave varying with explosion center distance at different monitoring points

2.4.4 不同监测点处水击波振动速度时程曲线

提取水下不同钻孔爆破监测点处水击波的峰值振动速度得到其随爆心距的衰减曲线如图9所示。

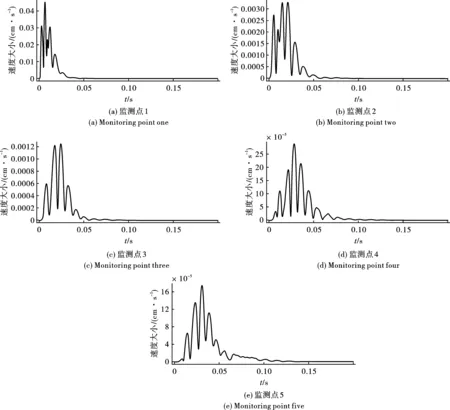
图9 不同监测点处水击波振动速度时程曲线Fig. 9 Time history curve of surge wave vibration velocity at different monitoring points

从图9可以看出,随着监测点1～5的爆心距依次增加,每个监测点位水击波振动速度达到峰值的时间逐渐增加,分别为0.006 s、0.021 s、0.025 s、0.028 s、0.031 s,水击波峰值速度出现的时间随着爆心距的增加也依次增加,表现出同步性。此外,爆破振动速度峰值在靠近爆源处最大,主要原因是炸药在水域中爆炸产生的水击波压力以背向炸药的方向向外传播。爆心距越大,爆破振动速度越小,水击波的影响范围就越小。

从图10可以看出,各测点水击波峰值速度拟合曲线为y=1.6402e-0.1284x,相关系数R2=0.9994,说明该曲线拟合精度高,可以较好地反映出水击波的峰值速度随爆心距变化呈指数衰减规律,可为预防爆破水击波灾害效应提供依据。同时,在当前的炸药当量下,所布置的监测点水击波振动速度总体较低,爆心距从28 m增加到48 m时,水击波峰值振动速度下降较快,以监测点1峰值振动速度为基准,在爆心距48 m时其峰值振动速度下降到仅为爆心距28 m处监测点处峰值振动速度的7.3%,衰减率达到了92.7%;爆心距为68 m处的监测点3峰值振动速度衰减为2.6%,衰减率为97.4%;到爆心距为108 m处的监测点5时,其振动速度仅为监测点1振动速度的0.37%,衰减率达到96.3%;从爆心距48 m的监测点2处开始,水击波峰值振动速度的下降幅度较小,到爆心距108 m的监测点5,水击波振动速度已经可以忽略,不会对建(构)筑物产生影响。

图10 水击波峰值振动速度随爆心距变化曲线Fig. 10 Curve of peak vibration velocity of surge wave varying with distance between explosion centers

3 现场监测

根据地质勘查资料,结合现场考察调研,在坝体上方布置5个监测点,分别距离水库边缘1.3 m(1#)、5.4 m(2#)、7.7 m(3#、4#、5#),水下爆破钻孔点到大坝的距离为18 m,每个监测点处布置一台L20-N型爆破振动仪,且X方向指向爆破点。主要参数为:采样频率为10 200 Hz,触发方式为电平内触发,触发电平为0.050 cm/s,存储时长为2 s。同时,在水域中布置3个监测点,距离爆破点的直线距离由近到远分别为5.1 m、10.6 m、15.3 m,每个监测点处布置一台LS1206B明渠流速计(采样频率为每隔2 s采集1 s,触发方式为机械触发,灵敏度为0.001 m/s,存储时长为1 h)和一台M20液位水压力计(采样频率为4 Hz,触发方式为机械触发,灵敏度为1 Pa,存储时长为4 h),水压力计和明渠流速计垂直布置,三个水压计分别固定在距离水面1.8 m、4.0 m和6.0 m处,明渠流速计固定在距离水面1.8 m处。现场照片如图11所示。

图11 现场监测点布置示意图Fig. 11 Layout of on-site monitoring points

为验证数值模型的可靠性,将现场测试工况瞬态求解模型结果与现场监测数据进行对比。测试工况瞬态求解模型根据图11的现场测点布置进行对应模型点添加,并按施工工况布设了爆破荷载进行求解。重点选取距离坝体较近的1#与2#测点进行对比分析,得到数值模拟与现场实测的X、Y、Z三个方向的峰值振速和合振速的对比结果(见表3)。显然,远离爆破点的2#测点相比1#测点的合速度峰值和Z方向速度峰值有所减少,但X方向和Y方向的振动速度峰值则有所增加,主要原因是由于爆破能量传播扩散造成的,远处测点的弹性波与X、Y方向的夹角更小,更多地分解为X、Y方向振动速度。此外,取更靠近爆破点1#测点的现场测试与数值模拟速度时程曲线进行对比分析,如图12所示。

表3 现场测试与数值模拟峰值振动速度对比Table 3 Comparison of peak particle velocity between field test and numerical simulation

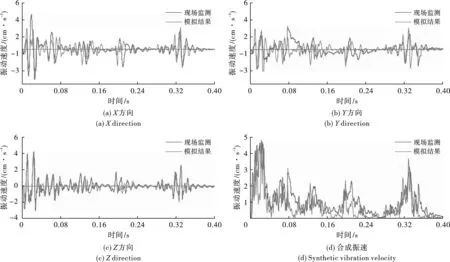
图12 现场测试与数值模拟速度时程曲线对比Fig. 12 Comparison of velocity time curve between field test and numerical simulation

从图12可以看出,数值模拟与现场监测结果具有较好的一致性,数值模拟中Z方向振动速度和合速度时程与现场监测结果变化规律高度相似且峰值略大于现场测试结果,但X、Y方向的振动速度波形相似度相对较低,可能原因是数值模拟中没有考虑现场测试所在区域的泥盆系基岩节理裂隙发育以及工程填土的复合作用,而Z方向的速度因为工程岩土质在垂直方向上较密集,具有较高的准确度。比较发现监测点的合振速最大误差为2.1%,认为在可接受的允许误差范围内,进一步说明了数值模拟结果的可靠性。

进一步地,水域各监测点的水下钻孔爆破监测结果如表4所示。可以看出,两次水下爆破监测的水流速度峰值基本接近且都很小,最大值为0.007 m/s,说明在距离爆破点较远的地方,水的流动性很小,可以忽略水流速度对水下爆破的影响。此外,水下钻孔爆破荷载作用下水击波的峰值压力均随爆心距、测深的增加而逐渐减小,爆心距越大,爆破产生的水压力峰值越小,与数值模拟结果变化趋势相同,主要原因是由于爆破产生的冲击能量随着传播而分散,再加上阻尼作用的影响所致。

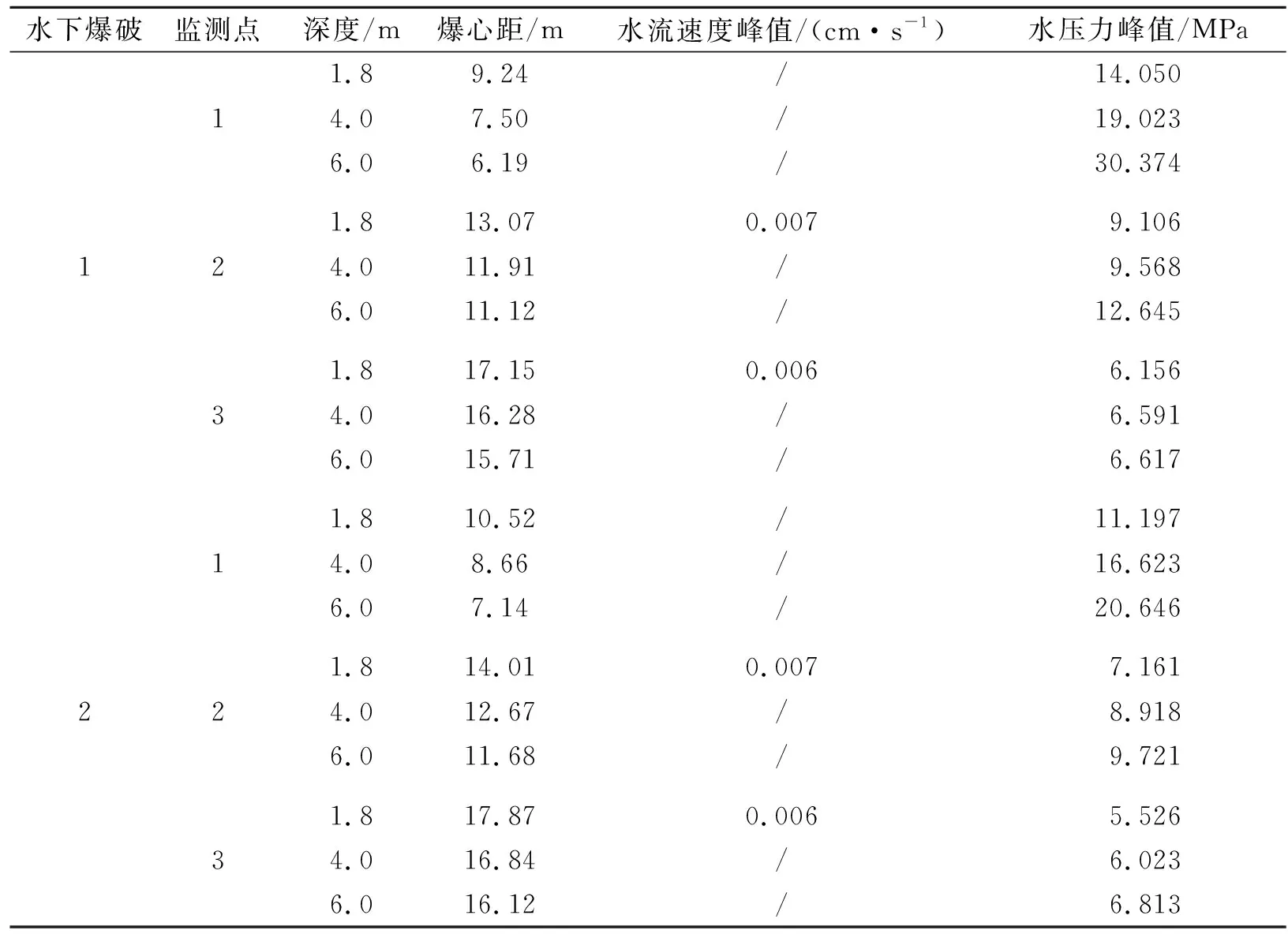
表4 水下钻孔爆破水域监测结果统计Table 4 Statistics of monitoring results of underwater drilling and blasting water area

4 结论及讨论

(1)水下钻孔爆破荷载作用实质是以爆破点为中心向四周传播,引起爆破点不同距离区域内的水体介质速度发生变化,随着时间的推移,水击波等值面由规则圆球形向非规则椭球形演变,在距离爆破点较远的水域中形成反射稀疏波。随着水介质速度阈值增大,爆破产生的水击波作用区域迅速减小,水击波影响范围较小。

(2)水击波应力传播在爆破分段延时情况下的不同位置具有叠加效应,存在多个峰值,随爆心距的增加呈指数衰减规律,且衰减速率也呈指数下降。当爆心距越小,水击波峰值应力下降速度越明显,当爆心距达到68 m时,水击波峰值应力下降变得很小,可以基本忽略。

(3)水击波振动速度随爆心距的增加呈指数衰减,在当前的炸药当量下,所布置的监测点水击波振动速度总体较低,当爆心距从28 m增加到108 m,水击波峰值振动速度衰减率达到96.3%,基本上不会对构筑物产生影响。此外,水击波振动达到峰值速度出现的时间随爆心距的增加也逐渐增大,分别为0.006 s、0.021 s、0.025 s、0.028 s、0.031 s,表现出同步性。

(4)数值模拟结果与现场监测对比分析得出模拟误差较小,且爆破振动速度变化规律大致相同,本文建立的数值模型具有可靠性。但考虑水下钻孔爆破施工的复杂性及不可预见性,爆破参数、岩体损伤与发育程度、水位变化、炸药包及装药量等对水击波传播规律影响较大,后续将进一步开展水下钻孔爆破多因素耦合作用下数值仿真分析,使计算结果更接近实际情况,更好地指导爆破施工。