基于振荡水柱原理的大型海洋浮标供电系统设计及优化

谭梦琳，刘 臻*，张晓霞，李开开

（1. 中国海洋大学 工程学院, 山东 青岛 266100；2. 中交上海航道局有限公司, 上海 200000）

根据HY/T 037—2017《海洋资料浮标作业规范》（全国海洋标准化技术委员会, 2017），海洋浮标按直径不同可分为：小型浮标（直径≤3 m）、中型浮标（直径3～10 m）和大型浮标（直径≥10 m）。大型海洋浮标主要进行海洋气象观测工作，此外也可搭载水文、生态等观测设备进行额外的数据观测工作，需要离岸进行长期、连续的测量以及实时的数据传输，是海洋观测的主要手段，为海洋气象预测、海上油气等资源开发、港口建设及海上国防建设等提供重要的环境条件信息（尹路等,2013; 戴洪磊等, 2014）。近年来的“圆规”“梅花”“海葵”等台风的气象观测资料都能由位于东海的中国科学院东海海洋科学综合观测浮标所观测到，而独立、稳定的供电系统是这些观测工作顺利开展的保障。

目前海洋浮标主要使用太阳能与蓄电池的混合供电系统，受昼夜交替、日照时长和海上高盐高湿环境影响较大，维护成本高，光伏板污染也同样限制了系统发电效率（刘野等, 2017; 吴明东等,2021）。而浮标处于蕴含巨大能量的海洋中，其中波浪能作为海洋能中分布广泛、能流密度高且能量捕获便利的可再生能源（ Falcao et al, 2016; Mustapa et al, 2017; 史宏达等, 2021），具有不间断获能的特点，利用其为浮标供电可有效保证浮标的持续工作。

在20 世纪40 年代后半期，日本海军军官Yoshio Masuda 就已经开始研究利用波浪能为导航浮标供电，其研发的波能供电浮标也是漂浮式振荡水柱波浪能发电装置的雏形（Henriques et al, 2016）。自1965 年开始，这种波能供电浮标就在日本大量商业化生产应用，也是第一个成功部署到海洋中的波浪能发电装置（Henriques et al, 2016）。葡萄牙的Gomes 等（2012）采用一种基于频域分析的随机水动力学方法优化浮式OWC 几何结构，主要研究了不同的浮体直径和中心管总淹没长度对年平均功率的影响[15]。基于Gomes 等（2012）的几何结构优化结果，Henrigues 等（2016）将其应用于自供电传感器浮标，进一步通过数值模拟计算，研究了Spar-buoy OWC 和CD-OWC 两种形式的振荡水柱发电装置的水动力性能，并分别优化了2 种形式的PTO（Power Take Off）尺寸及选型。但这些工作均针对中小型浮标。国内对振荡水柱浮标供电的研究也主要针对于中小型浮标（宋洪侠等, 2014; 王广大,2017）。而中小型浮标由于装载设备较少，对海洋的探测能力有限，更全面的海洋监测任务需要大型浮标完成。因此本研究基于振荡水柱原理设计了一种针对大型海洋浮标的波浪能供电系统，并在已有物理模型试验的基础上，进一步通过数值模拟方法对浮标波能供电系统进行结构优化，为大型海洋浮标的原位供电提供了一种新的思路，同时揭示了耦合装置的水动力学特性，加强了装置的获能效益。

1 浮标波能供电系统设计

大型海洋浮标为搭载监测设备的大型圆盘形浮体，本研究设计的基于振荡水柱原理的大型浮标波能发电系统如图1 所示，与水体接触部分为浮标圆盘主体，因此简化了浮标上部监测设备。波浪能发电装置一般包括三级能量转换系统，浮标底部开一圆柱形孔作为气室，气室内液面振荡使气室内部空气产生压强变化，将波浪能转换为空气动能，作为波浪能一级俘获系统；开孔顶部连接空气透平，将空气动能转换为机械能，作为装置二级能量转换系统；电机内置于透平尾部，空气透平旋转驱动电机发电，将机械能转换为电能给浮标供电，作为三级能量转换系统，相关电气设备及蓄电池布置于透平两端。

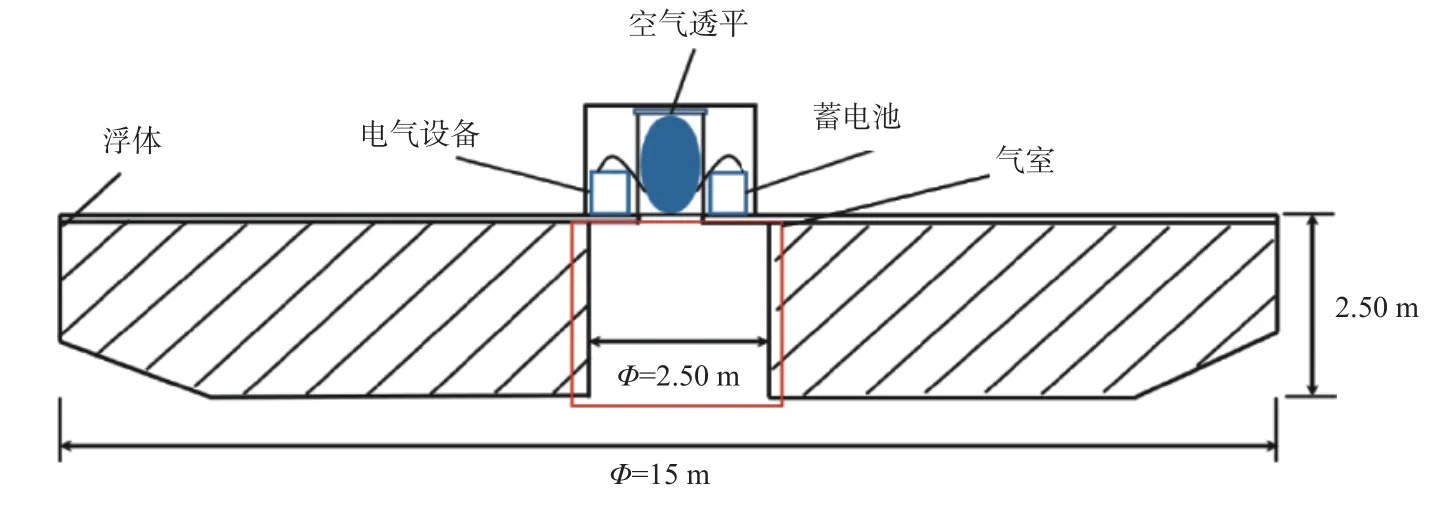
图1 浮标波能供电系统剖面示意图Fig. 1 Schematic diagram of the section of the buoy’s wave-energy power supply system

2 物理模型试验概况

物理模型试验在山东省海洋工程重点实验室进行，试验比尺 λ=10，试验装置如图2 所示，装置一级能量转换系统的气动性能是试验研究重点，因此简化了二、三级能量转换系统。装置整体为圆台形，直径为1.500 m，高0.025 m，气室直径为0.250 m，由铝合金制成；顶部开一直径为0.025 m的圆形孔板，用来代替空气透平所产生压降。试验采用三点系泊，系泊方式为张紧式。张紧式系泊一般由顶部、中部、底部三部分组成，顶部和底部采用较短的锚链以抵抗长时间的摩擦，中间部分采用张紧的系泊缆来控制浮体的运动（王宏伟, 2011）。由于本试验主要研究装置的气动性能且受限于试验条件，对系泊缆进行了适当简化。系泊缆的顶部和底部采用锚链材料，中部采用钢丝绳满足系泊所需长度，系泊的张紧恢复力由顶部增设的弹簧提供。试验结果表明，装置主要在入射波方向剖面（纵剖面）运动，运动响应主要为垂荡和纵荡，并且发现此模型虽然可以保证浮标正常工作，但在目前结构形态下装置俘获宽度比较低，为提高气室捕能效率，进一步利用数值计算方法对模型进行结构优化研究。试验场地布置如图3 所示。

图2 物理模型试验装置Fig. 2 Device for the physical model test

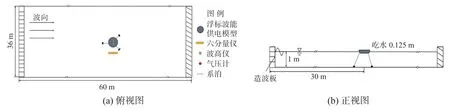
图3 试验布置示意图Fig. 3 Schematic diagram showing layout of the test

3 装置结构优化研究

3.1 数值模型构建

由物理模型试验结果可知，装置主要在波浪入射方向剖面运动，因此本研究利用ANSYS-fluent软件，采用二维数值模型进行计算。建立的浮标波能供电系统二维模型示意图及数值模型网格设置如图4 所示，同样简化二、三级能量转换系统。装置主体为圆台形，直径为1.50 m，高0.25 m，气室直径为0.25 m，顶部孔板开孔面积为液面面积的1%。利用ANSYS-ICEM 软件进行网格划分，由于涉及到浮体的运动，在装置区域使用非结构化网格，其具有良好的适应性；两端区域为结构化网格，可以大幅减少网格数量，并且规则的网格排列可降低不必要的数值耗散，提高计算精度与效率。为了捕捉到更精确的自由水面和装置周围流体的运动，在自由表面及装置周围进行了网格加密。

图4 二维模型示意图及数值模型网格设置Fig. 4 2D numerical model and grid settings

装置的运动由ANSYS-Fluent 中的动网格技术、Six DOF 技术以及用户自定义函数（UDF）共同完成。其中动网格技术与Six DOF 可以实现装置的自由运动，UDF 进行装置系泊力的模拟。物理试验中模型采用张紧式系泊，故单根系泊的系泊力可以由式（1）表示。由于对气室气流速度起主要影响的为垂荡运动，因此在二维数值模拟中初步研究装置在垂荡运动下的性能响应。由于试验为三点系泊，故加载在装置上的系泊力可由式（2）表示：

式中：Fk为单根系泊的系泊力；F0为单根系泊的预应力；k为单根系泊的弹性系数； Δl为单根系泊的伸长量；Fky为加载在装置上的系泊力；F0y为F0的y向分量；ky表示单根系泊的y向弹性修正系数；Δy表示装置的垂荡位移， Δy可由Fluent 中的Six DOF 技术读取。

3.2 数值模型的验证

为保证所构建浮标波能供电数值模型的可靠性，需对模型进行运动和气动响应验证。如图5 所示，y*表示装置垂荡幅值与波高H的比值，p*=p/(ρairgh)、h*=h/H分别为压强与液位的无量纲数，红线代表数值模拟结果，蓝色小方块表示物理试验结果。误差结果表明，装置运动响应与气动性能的数值模拟与试验结果拟合较好，整体趋势相吻合，垂荡响应与3 种气动性能参数皆随周期增大呈下降趋势。在周期T=2 s 以前，装置在运动与气动性能上的误差值极小，不超过8%，而在周期逐渐增大的过程中，出现了4 种参数幅值略微偏大的情况，在周期T=2.5 s 时较明显。初步推断，由于数值模拟限制了纵荡方向位移，而试验中周期越大纵荡位移越大，因此大周期处更剧烈的纵荡位移所含能量被转换为垂荡方向能量，导致装置在大周期时的垂荡幅值误差增大。而垂荡位移的增加进一步造成装置和水体相对运动幅度增大，使气室液位与气室液面速率增大，从而导致气室空气受挤压程度变大，气室压强增大。但整体来看，装置运动与气动响应误差均在合理范围内，能保证数值模型计算的准确性。

图5 装置垂荡响应及气动性能误差分布Fig. 5 Motion response and aerodynamic performance error of the device

3.3 结构优化参数

为使模型更具实际参考意义，将装置还原为实际浮标尺寸：直径为15.0 m、高为2.5 m、气室直径为2.5 m、孔板面积为气室液面面积的1%，数值水槽也同比扩大，水深为10 m、吃水为1.25 m。根据国家海洋科学数据中心（2020）青岛小麦岛的波浪条件，取波高H=0.8 m，周期T分别为4 s、6 s、8 s、10 s 和12 s，结构优化从气室直径尺寸、孔板尺寸和双气室开孔间距三个方面展开。气室直径尺寸直接影响装置的波浪俘获能力，透平产生的压降也会影响气室的气动性能，在此气室尺寸和孔板尺寸基础上，进行双气室开孔间距的优化研究。以气室俘获宽度比CWR 作为装置的气动性能评定参数，如式（3）所示：

式中：Pair为气室空气功率；Pwave为波浪功率；L为装置的能量俘获宽度。规则波下的波浪功率和气室空气功率分别如式（4）和式（5）所示：

式中： ρw为水的密度；ζ为入射波振幅；p(t)为气室内空气压强；q(t)为空气流量；t0为某一时刻值；n为自然数；Cg为波能传播速度，计算式为：

式中：k为波数；h为水深。

4 优化研究结果及分析

4.1 气室尺寸优化

装置在不同气室直径下的气动性能如图6 所示，气室直径比Ld为入射波长 λ与气室直径d之比，气室直径在2.5～6.0 m 等间隔取值。气室压强随Ld增大而增大，空气流量随Ld减小而减小，空气功率和俘获宽度比随Ld增大呈先增大后减小趋势，均在Ld=5.5、d=4.5 m 时分别取得最优值511 W、0.198 m-1。其中入射波周期越小，装置气动响应越大，变化幅度也越大。图7 为周期T=4 s 情况下，d分别取值3.0、4.5 和6.0 m 时的水体流场和空气流速图。由图7 可知，气室直径越大，气室液面速率越低，导致内部压强越小，但气室尺寸增大相应空气流量同样增大，流速变大，因此空气功率和俘获宽度比综合压强与流量因素，在Ld=5.5、d=4.5 m 时取得最优值。

图6 装置气动性能随波长气室直径比Ld 变化Fig. 6 Changes of the aerodynamic performance of the device with the wave length to gas chamber diameter ratio Ld

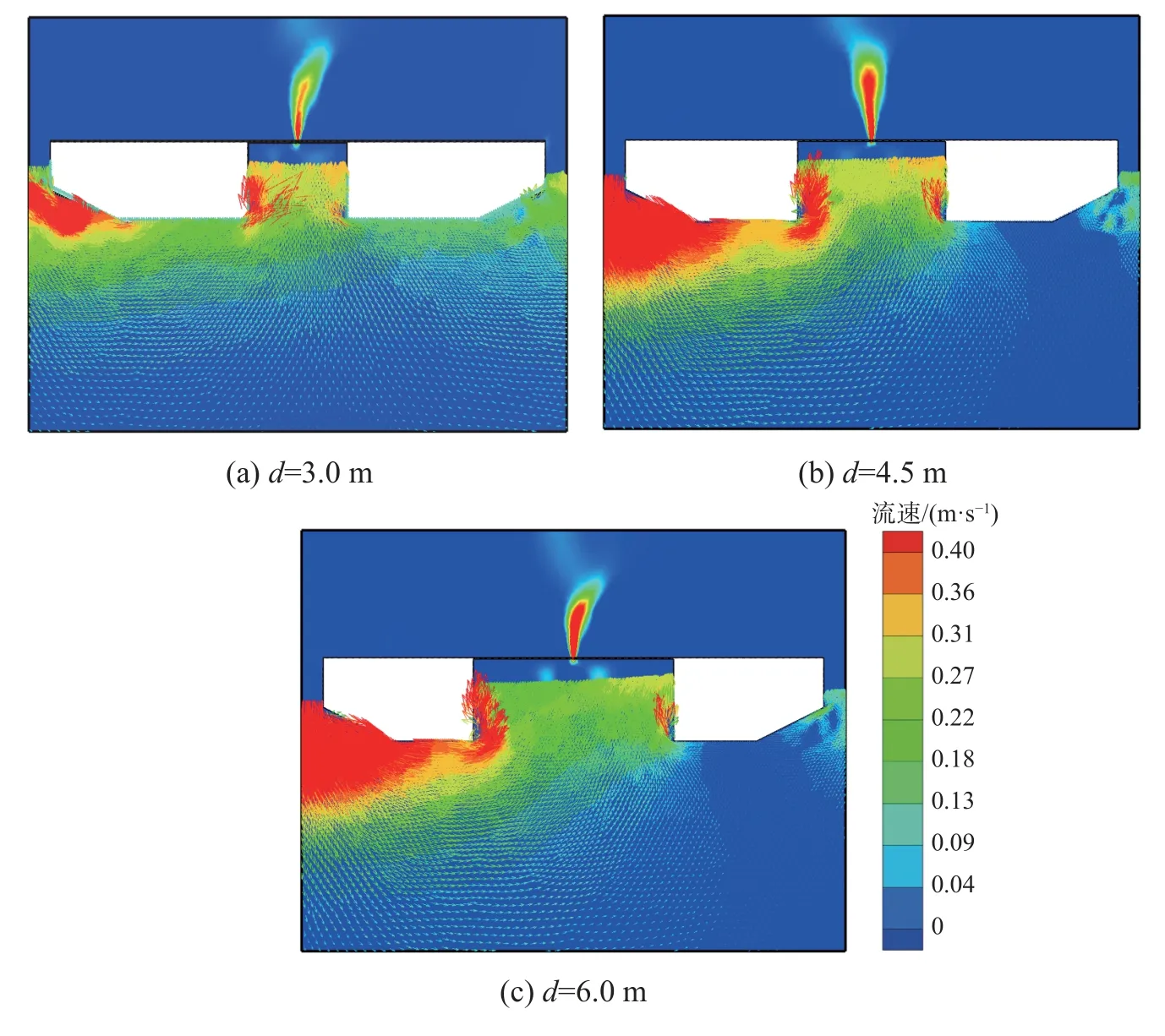
图7 不同气室直径情况下装置周围流场与空气流速分布Fig. 7 Distributions of flow field and air flow velocity around the device under different gas chamber diameters

4.2 孔板尺寸优化

装置在较优气室直径基础上，进行孔板尺寸优化，孔板面积与液面面积比e的取值范围为0.25%～2.25%，结果如图8 所示。可以看出，随着e增大，气室压强逐渐减小，空气流逐渐增大，空气功率和俘获宽度比呈先增大后减小的趋势；其中周期越小气动性能响应越大，在周期T=4 s、e=1.25%处空气功率和俘获宽度比分别取得最大值555 W、0.223 m-1。分析推断，孔板尺寸越大，气室排出气体所受阻力越小，因此气室压强越小，而空气流量与过流面积和流速正相关，面积的量级小于流速，因此面积的变化量影响较大，故e越大流量越大。

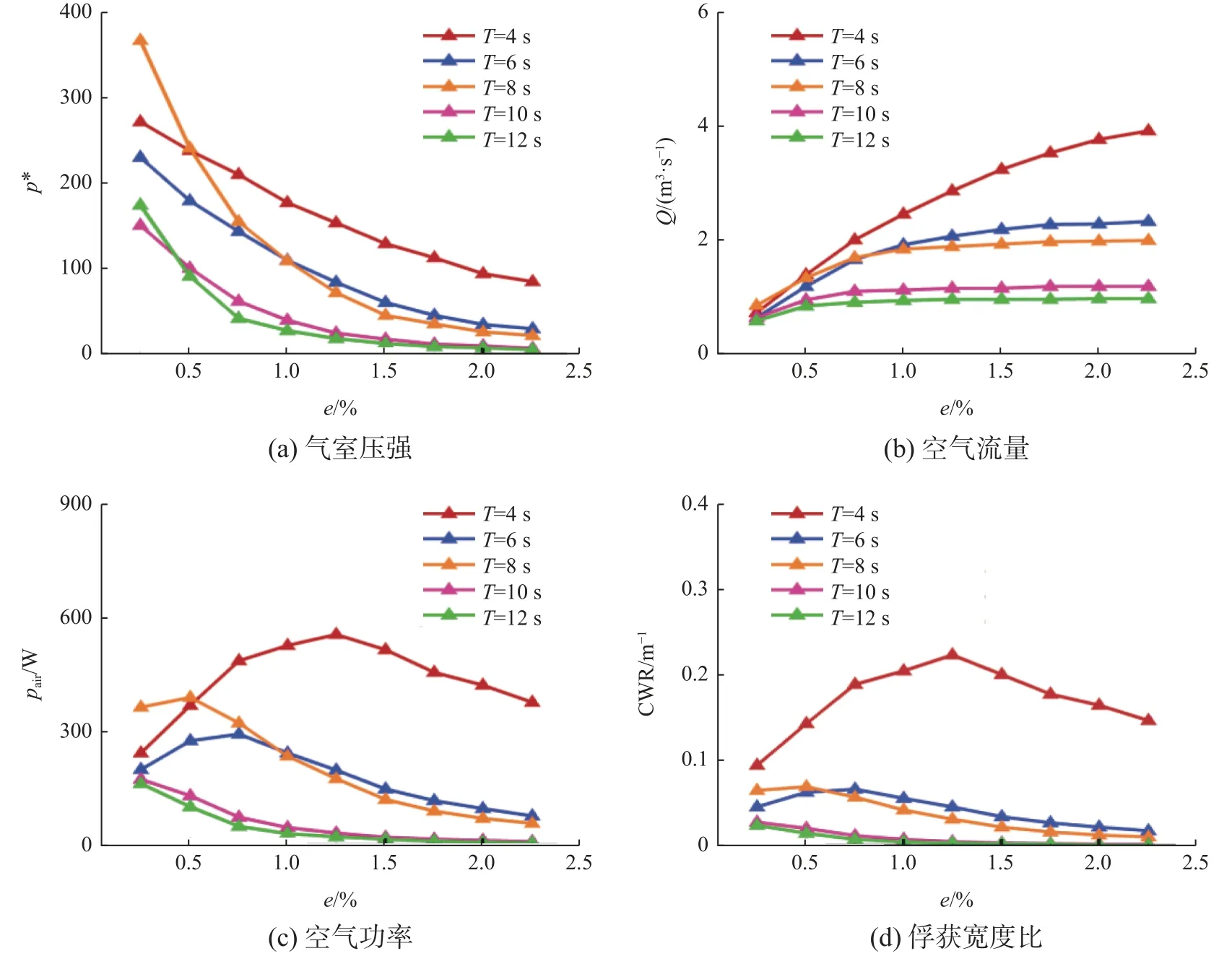
图8 装置气动性能随孔板面积比e 的变化Fig. 8 Changes of the aerodynamic performance of the device with the orifice area to plate area ratio e

4.3 双气室及其间距影响

为充分利用大型海洋浮标的体积优势，以气室尺寸：直径d=4.5 m、e= 1.25%为基础，保证总气室液面面积不变，将气室增加到2 个，2 个气室直径d1=d2=d/2D，其中D为浮标直径，如图9 所示，c为气室间距。图10 为装置在不同气室间距比Lk= λ/c下的气动响应情况，气室压强、流量、空气功率和俘获宽度比均随Lk的增大呈先增大后减小的趋势，且周期越小响应越大，在周期T=4 s、Lk=7时有最大功率和俘获宽度比，分别为680 W、0.26 m-1。装置在T=4 s 时，呼气时刻流场流速如图11 所示，k=c/d，随着气室间距增大，左边气室水体流速和空气流速逐渐增大至稳定，右边气室水体及空气流速先略微增大后减小，因此在Lk=7，即k=0.75处，左右气室的综合功率及俘获宽度比取得最大值。

图9 双气室结构示意图Fig. 9 Schematic diagram of the double air chambers

图10 装置气动性能随波长气室间距比Lk 的变化Fig. 10 Changes of the aerodynamic performance of the device with the wave length to air chamber spacing ratio Lk

图11 不同气室间距情况下流场与流速分布Fig. 11 Distributions of flow field and air flow velocity around the device under different gas chamber spacing k

5 结 论

本文设计了基于振荡水柱原理的大型海洋浮标波能供电系统，并构建了其二维数值计算模型，通过与试验的运动与气动响应对比验证了其可靠性。得到主要结论如下。

1）气动性能对入射波周期的变化较为敏感，小周期波的获能效益更大，在所研究入射波周期范围内，周期T=4 s 时气动响应最大，大周期波T=10 s 和12 s 几乎没有波能俘获能力。

2）装置的功率与俘获宽度随气室直径比的增大先增加后减小，在Ld=5.5 时取得最优值，分别为511 W、0.198 m-1，较优气室直径d=4.5 m。

3）随着孔板面积比e增大，装置功率与俘获宽度比先增大后减小，在e=1.25%处分别取得最优值555 W、0.223 m-1。

4）随着双气室间距比Lk增大，装置功率与俘获宽度比呈先增后减趋势，在Lk=7、气室间距k=0.75 时，分别取得最优值680 W 和0.26 m-1。