基于RBFNN的跨座式单轨车辆自动驾驶滑模控制研究
,刘浩鸣,杜子学,邬浩鑫 ,侯忠伟
(1.重庆交通大学 机电与车辆工程学院,重庆 400074;2.重庆交通大学 交通运输学院,重庆 400074)
0 引 言
随着人工智能、互联网等新技术发展,城市轨道交通驾驶的自动化成为了国内外发展趋势。在日本、韩国、法国以及新加坡等地及我国上海地区均有全自动驾驶的城市轨道交通线路。城市轨道交通列车的自动驾驶可有效提升运行效率,降低运营成本,减少工作人员失误,提升列车运行品质[1]。
跨座式单轨交通是城市轨道交通的一种典型制式,相较地铁交通具有成本低、噪音低、转弯半径小等优点,是城市轨道交通建设的重要选择。重庆轨道交通2、3号线是我国目前成功运营的中大运量跨座式单轨交通线路。现行重庆跨座式单轨是以ATO模式即半自动驾驶的方式运行,为提升跨座式单轨交通的运行效率,进行跨座式单轨交通全自动驾驶关键技术研究很有必要。
控制算法是保障跨座式单轨全自动驾驶的核心技术之一,已有的城市轨道交通全自动驾驶相关控制技术及控制算法,是开展跨座式单轨全自动驾驶研究的重要借鉴与基础。目前主流的城市轨道交通自动控制算法有经典PID算法以及基于PID的改进算法[2-3]、基于有限时间控制理论的算法[4-5]、滑模算法[6]、神经网络优化算法[7-8]等。PID算法依赖精确的模型,鲁棒性上有所欠缺;有限时间算法中收敛时间的上界一定程度上取决于系统的初始状态,限制了工程实际应用;滑模算法具有强鲁棒性、实时性好的优点,同时神经网络也可以优化模型和系统。V.ANDRIEU等[9]最早提出了固定时间稳定的概念;A.POLYAKOV[10]提出了固定时间Lyapunov稳定性理论。
借鉴以上研究,笔者提出了一种基于径向基神经网络(RBFNN)的跨座式单轨固定时间滑模控制方法,以提高鲁棒性和工程实用性。首先建立基于RBFNN的跨座式单轨动力学模型,提出了基于RBFNN的跨座式单轨固定时间滑模控制算法,设计基于RBFNN的跨座式单轨固定时间滑模控制器(后称RBFFTSMC),并通过数值仿真验证所提出的控制算法的有效性。
1 跨座式单轨动力学模型
跨座式单轨动力学模型是控制方法研究的基础。基于质点模型的指导思想和列车牵引动力学理论,进行跨座式单轨运行受力分析,详细的动力学模型见文献[11]。
文献[11]中f2(p,v,t)作为附加运行阻力,包括曲线阻力、坡道阻力、隧道阻力以及其他因素导致的阻力,受时间、区段影响很大,难以建立统一精确的模型,可将其看作是关于位置、速度的时变函数。利用RBFNN可以逼近任意非线性函数的特性来逼近f2(p,v,t)以达到提高控制精度的目的。RBFNN是一种前馈神经网络, 它由输入层、隐含层、输出层共三层网络构成, 其网络结构如图 2。
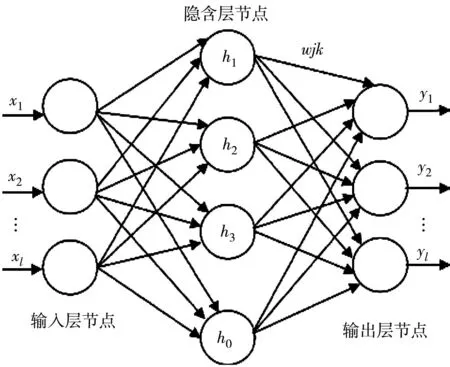
图1 RBFNN结构
输入层如式(1):
X=[x1,x2,…,xl]T
(1)
式中:l为输入的维数。
隐含层如式(2):
h=[h1,h2,…,ho]T
(2)
式中:o为隐含层节点个数。
用高斯函数作为基函数则有:
(3)
式中:Cj为隐含层高斯基函数的中心向量;σ为隐含层高斯基函数的宽度。
神经网络权值如式(4):
W=[w11,…,wjk]T
(4)
输出层如式(5):
Y=[y1,y2…,yl]=WThj(x)
(5)
用RBFNN来逼近f2(p,v,t),神经网络的理想输出如式(6):
f2=W*Th(x)-ε
(6)
式中:W*T为RBFNN理想权值;h(x)为隐含层高斯函数输出向量;ε为逼近误差。
定义神经网络的实际输出如式(7):
(7)

定义RBFNN误差如式(8):
(8)
定义RBFNN权值误差如式(9):
(9)
取如式(10)的状态变量:
(10)
综合式(1)~式(10),可以得到基于RBFNN的跨座式单轨的动力学模型为:
(11)
2 跨座式单轨固定时间滑模控制
跨座式单轨在行驶中目标是准确跟踪控制中心发出的或预先设定的速度-距离曲线指令。
2.1 控制器设计
为方便RBFFTSMC设计,给出如下引理:
引理1[10]对于非线性系统式(11),如果存在一个连续径向无界函数V:Rn→R+∪{0}满足:
V(x)≤-k3Vz(x)-k4Vg(x)
(12)
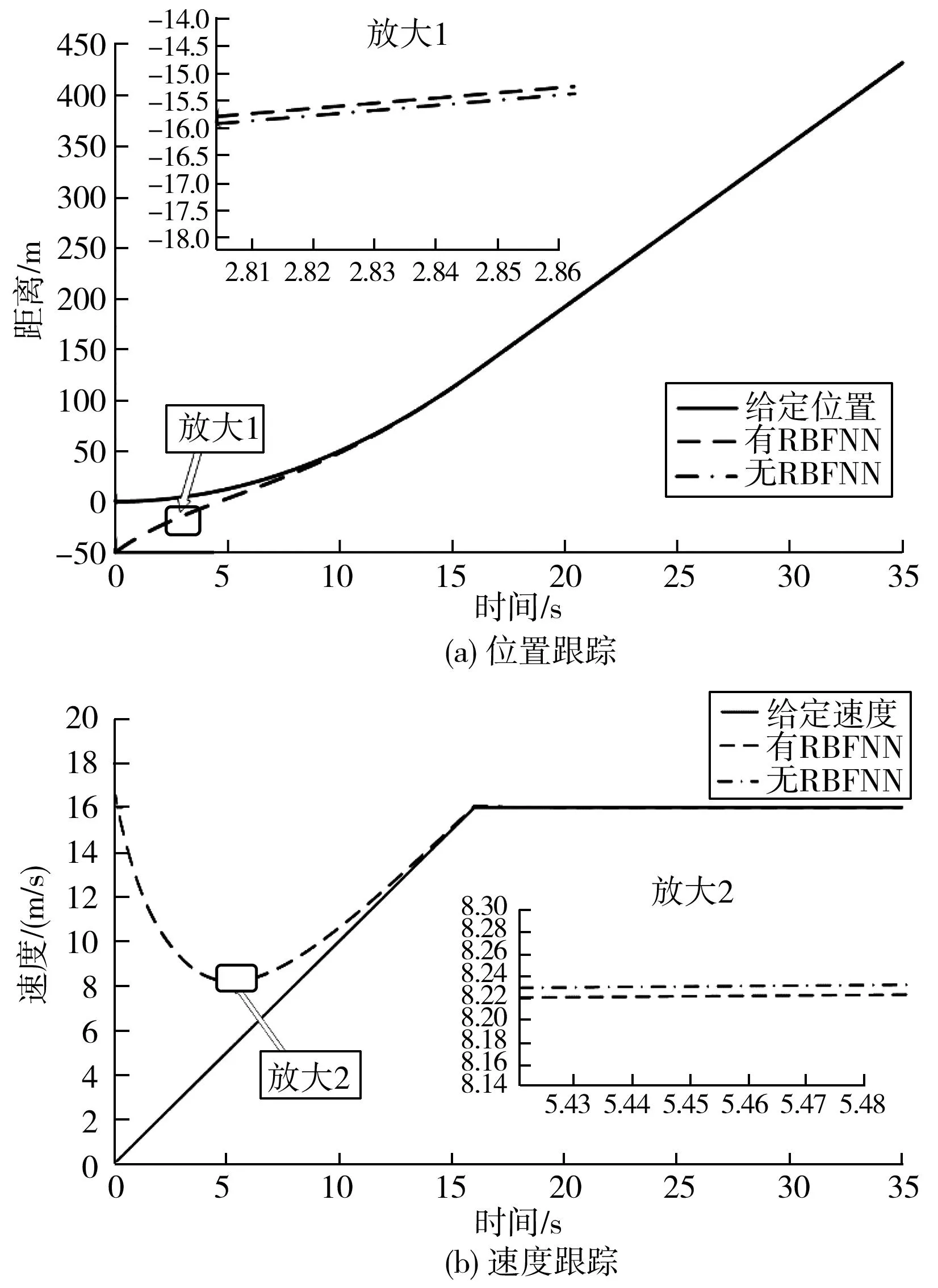
式中:k3,k4>0,z>1,0 此时系统式(11) 为全局固定时间稳定, 其收敛时间T1满足: (13) 引理2对于非线性系统式(11),如果存在一个连续径向无界函数V:Rn→R+∪{0}满足: V(x)≤-k3Vz(x)-k4Vg(x)+η1 (14) 式中:k3,k4>0,z>1,0 此时系统式(11) 为实际固定时间稳定[12-13], 其收敛时间T2满足: (15) 式中:ζ为正的常数, 并满足0<ζ<1。 式(11)解的残差集为: (16) 对于跨座式单轨车辆,给出如下定义: (17) 式中:ep为跨座式单轨车辆位置误差;pr为车辆位置指令;p为车辆位置;ev为车辆速度误差;vr为车辆速度指令;v为车辆速度。 为同时兼顾收敛速度和平滑性,选取滑模面s如式(18): (18) (19) 式中:γ2,β2为正数;z2,n2,g2,q2为正奇数,且满足z2>n2,g2 对式(18)求导得到: (20) 式(20)结合式(11)、式(17)可以得到: (21) 式(21)结合式(19)可以得到: (22) (23) 定理1对于非线性系统式(11)的跨座式单轨车辆,当选用滑模面式(18)及控制器式(22)时,系统为全局稳定且满足跨座式单轨车辆位置误差ep和速度误差ev于固定时间Tp内收敛至零, 其中Tp满足式(24): Tp≤T1+T2 (24) 即跨座式单轨车辆在固定时间Tp内跟踪到位置指令和速度指令。 证明:首先,当系统到达滑模面时,根据选取的滑模面式(18)可以有式(25): (25) 根据引理1可得滑模运动阶段的时间满足: (26) 再选取Lyapunov函数如式(27): (27) 对 Lyapunov 函数V2求导, 综合式(1)~式(11)、式(17)、式 (20),可得: (28) 式中:ε1为跨座式单轨车辆理想神经网络输出的逼近误差。 设计自适应律为: (29) 则有: (30) (31) 根据引理2,可得非线性系统式(11) 是实际固定时间稳定的, 收敛时间T2满足: (32) 式中:z=z2/n2,g=g2/q2 系统状态在固定时间T2内收敛到紧集Ω: (33) 证毕。 可以发现,笔者设计的控制器可以使跨座式单轨车辆在固定时间Tp内跟踪上预设的速度-距离曲线指令。 对笔者设计的控制算法进行仿真验证,构建跨座式单轨一般行驶场景。为了节约仿真时间,将仿真对象按比例缩小,对结果有效性没有影响。 仿真中将文献[15]中的有限时间滑模控制算法作为对比分析的对象,跨座式单轨车辆的质量为4 000 kg,初始位置为50 m,初始速度为-10 m/s,控制器参数设置可见文献[11]。 跨座式单轨在加速-巡航行驶时,笔者控制算法控制单轨车辆以及对比算法的位置和速度的追踪图如图2。 图2 加速-巡航行驶控制器跟踪对比 由图2可知:笔者算法控制车辆在15 s以内位置和速度均准确地跟踪到指令曲线,对比算法在24 s才跟踪到指令曲线。 笔者所设计控制器式(22)中,即使对附加运行阻力f2(p,v,t)做粗略的估计而不用RBFNN去逼近,跨座式单轨仍可在固定时间内跟踪到指令曲线,但是用RBFNN逼近运行附加阻力f2(p,v,t),可以使系统的响应更快,跟踪过程中的误差更小,下面进行仿真对比,仿真中两种算法的区别是有无RBFNN逼近附加运行阻力f2(p,v,t)。 仿真中假定,RBFNN的参数设置如下:神经网络权值W的初始值为零矢量,隐含层的中心矢量:Cj=[100,200,380,700,1 000,0,100,200,380,700,0];σ=30;结果如图3。 图3 加速-巡航行驶控制器有无RBF跟踪对比 由图3可知:领航车辆的初始位置和速度分别是-50 m,17 m/s,有RBFNN在位置跟踪上比无RBFNN更加接近位置指令约0.1 m,有RBFNN时在速度跟踪上比无RBFNN更加接近速度指令约0.01 m/s。 笔者进行了跨座式单轨全自动驾驶算法研究,结论如下: 1)提出了基于RBFNN的跨座式单轨固定时间滑模控制方法,运用RBFNN的逼近特性来逼近时变附加运行阻力f2(p,v,t),并设计了基于RBFNN的跨座式单轨固定时间滑模控制器。 2)对控制算法的有效性进行了仿真实验,结果表明,笔者设计的算法具有较强的鲁棒性和工程实用性。 3)笔者设计的有RBFNN控制器控制车辆在15 s以内位置和速度均准确的跟踪到指令曲线,具有较好的控制性能,收敛速度较快。
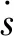
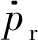
2.2 控制器稳定性证明
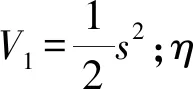
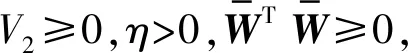
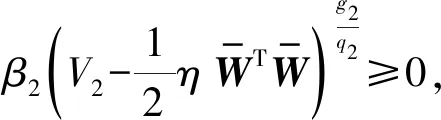

3 仿真实验
3.1 控制器仿真

3.2 有无RBFNN对比
4 结 论

