考虑实时载客量的公交信号优先策略改进控制模型
李淑庆,蒋雨洋,高铭仪,宾 科,陈 豪
(1.重庆交通大学 交通运输学院,重庆 400074;2.深圳城市交通规划设计研究中心股份有限公司,广东 深圳 518057;3.重庆市市政设计研究院有限公司,重庆 400020)
0 引 言
城市交叉口公交信号优先策略是公交优先的重要内容。传统公交信号优先策略一般是根据公交车到达交叉口时刻或公交车的固定载客量,采用绿灯延长或绿灯早启信号控制策略,优先放行公交车辆。但这种公交信号优先策略的对象是公交车辆,而不是公交车内的乘客,当公交车乘客量较少或为空车时,对公交车优先的意义就降低了。故需要依据公交车辆的实时载客量,协调公交车辆和社会车辆的通行需求,以交叉口通过的乘客为对象,研究建立公交信号优先策略的控制模型。
国内外学者对公交优先道和交叉口公交信号优先控制方法进行了较多研究,取得了一定成果。S.I.GULER等[1]和I.TARIKUL等[2]分别结合公交专用道和预信号设置方法,对公交优先控制进行了分析;H.A.AHMAD等[3]将公交车和社会车辆的行程时间、延误和停车次数等实测数据进行回归分析,得到了最优的干线公交优先信号方案;P.ANDERSON等[4]、B.D.LEONARD等[5]、宋现敏等[6]分别提出了“动态公交车道”、“公交与右转混合型专用道”等优先策略,实时分析了公交车到站准点率、动态变更交叉口信号时长,得到了公交优先的方案;柏海舰等[7]提出了在网联环境下,基于站点时刻表的公交信号优先方法,该方法能有效降低非优先相位延误时间,保障交叉口整体通行效率;单肖年等[8]、李津等[9]分别基于公交优先目标,设置了新型高乘载车道和柔性车道,通过车联网环境下元胞自动机模型得出了不同条件下的车道设置策略,降低了交叉口整体延误;SHU Shijie等[10]、刘畅等[11]分别提出了一种以公交载客量为定值和交叉口总乘客延误增量最小的公交信号优先模型;JIN Jing等[12]以交叉口服务水平最优为目标,提出了公交信号优先一次性补偿和分阶段补偿的策略;别一鸣等[13]提出了基于饱和度为约束条件的公交车有限优先策略;蒋瑶等[14]基于公交载客量的主观设置,以车辆通行延误和停车率最小为目标,建立了多目标快速公交优先配时模型;邓明君等[15]将公交优先与综合待行区策略相结合,通过仿真验证了设置基于公交优先的综合待行区能降低社会车辆和公交车延误。
学者们均是以公交相位绿灯延长或绿灯早启的公交信号优先控制策略为基础,以交叉口周期延误最小为目标,优先研究的对象大多是公交车辆,而不是公交车内实时载客量。即有些学者考虑了固定的公交载客量,按照人均延误最小为目标构建公交信号优先模型,也没有根据公交车实时载客量进行信号优先控制。故笔者利用公交车GPS和IC卡的数据进行匹配分析,得到了公交车到达交叉口实时载客量,提出了公交信号优先改进策略,综合考虑通过交叉口的公交实时载客量和社会车辆驾乘人员,构建以通过交叉口人均延误最小为目标的公交信号优先控制模型,并通过案例进行分析验证。
1 公交车实时载客量
1.1 公交车通过交叉口时上车总乘客人数
笔者以最多停靠4辆公交车的公交站台为目标,以公交站点经纬度坐标为中心,设置50 m的缓冲半径区域[16],将落到该缓冲区域内最早的公交GPS定位时刻作为公交车辆的到站时刻,如图1(a);某乘客在站点刷卡的IC卡数据,如图1(b)。

图1 基于IC卡和GPS数据融合的上车站点识别
由图1(a)可知:编号为82265的869路公交车在某工作日07:45:02—07:45:57,停靠于丁香路站。将图1(b)中的车辆编号和线路编号与图1(a)相同的关键字段进行对比可知:某乘客上车刷卡站点为丁香路站。根据该公交车所有乘客的刷卡数据,比对公交车进出站时刻和公交IC卡刷卡时间可知:公交线路各个站点的上车乘客数和公交车通过交叉口时上车总乘客数。比对步骤如下:
Step1:输入包含线路编号、车辆编号、刷卡时刻的IC卡和公交车定位时刻的GPS原始信息和命令;
Step2:定义新列表-车辆,比对包含相同车辆编号字段的IC和GPS的记录,存储在新列表-车辆中;
Step3:对于目标车辆i,选择IC记录,将它们存储在临时列表list-1中;选择GPS记录,将它们存储在临时列表list-2中;
Step4:对于list-1列表中目标车辆j:在列表list-2中比对公交车定位时刻和j的刷卡时刻最接近的GPS记录,并将上车站点名称及经纬度添加到j中;
Step5:输出带有上车站点名称及经纬度信息的IC卡数据;
Step6:利用Step4得到的IC卡数据,统计第δ个站点的上车乘客人数Zδ;
Step7:输出公交车通过交叉口时上车总乘客人数Pu:
(1)
式中:ρ为交叉口上游公交线路站点个数。
1.2 公交车通过交叉口时下车总乘客人数
将公交出行分为闭环和非闭环出行,分别利用不同方法推算乘客下车的站点。
1.2.1 闭环出行下车站点
图2为典型的(多条公交线路)闭环出行情况。某日某乘客从线路1的b1站点上车,换乘线路2、3后回到起点,形成完整闭环出行链,该乘客下车站点可认为是线路1中b1站点后续的任意一个站点。乘客闭环出行时,一般会选择在距离下一次上车站点步行距离或时间最短的站点下车。以500 m为有效搜索半径[16],比对线路1中b1站点各后续站点与线路2中b2站点之间的换乘时间和距离,视所有后续站点中换乘时间和距离最短的为下车站点,由此得出线路1中乘客下车站点为a1。
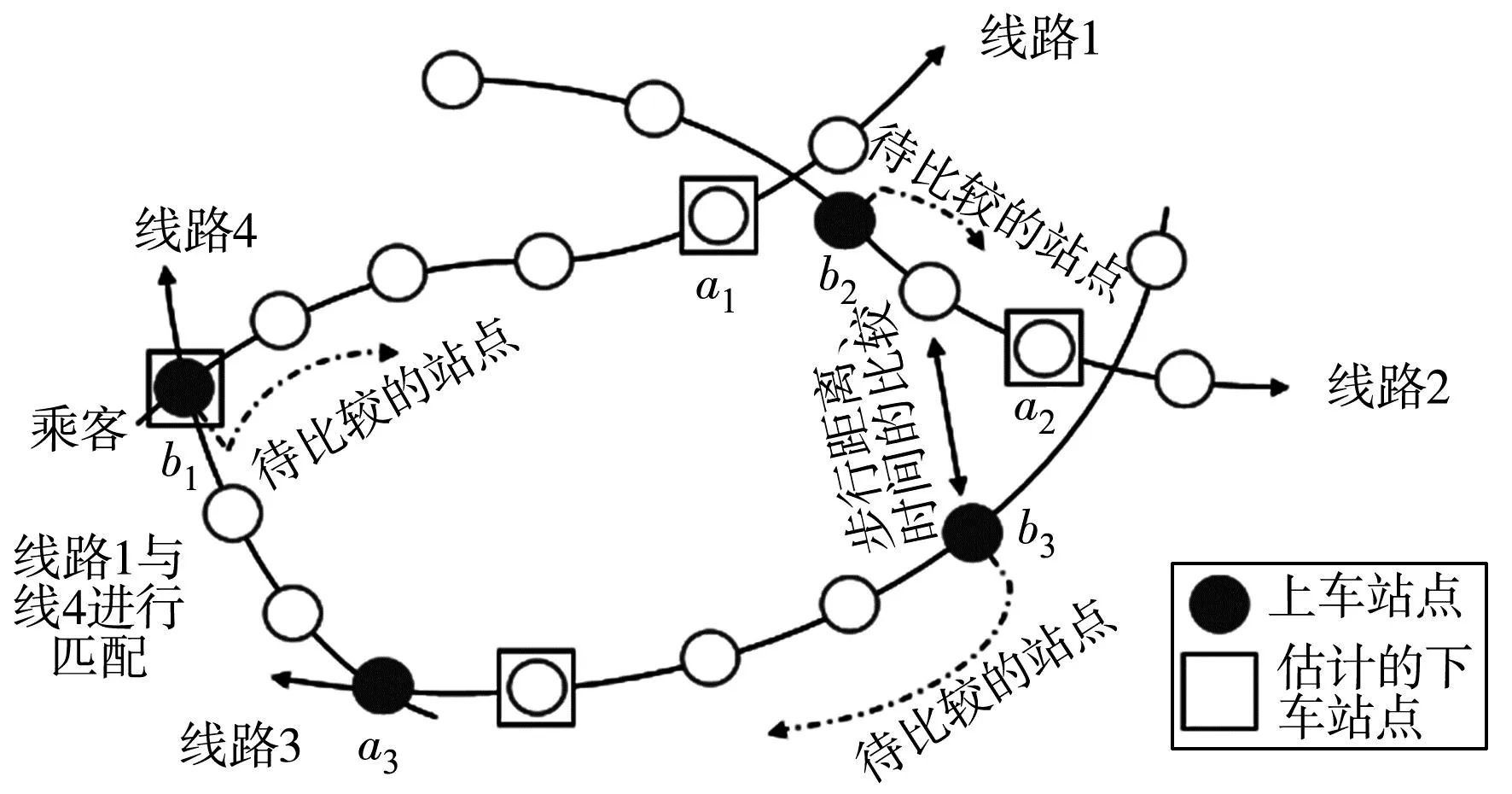
图2 乘客闭环公交出行
若当天乘客最后一次选择在a3站点乘坐线路4,则可认为线路4下车站点为当天首次出行线路1上车站点;同理,若次日首次出行选择相同线路,则可认为线路4下车点为次日出行上车点。
1.2.2 非闭环出行下车站点
图3为非闭环出行情况。若乘客第μ+1天非闭环出行一次,通过历史刷卡数据搜索相同IC卡号的出行记录,得出在第μ-1天和第μ+1天乘坐的是同一条公交线路,且上车刷卡时刻相差较小。故第μ-1天的下车站点可认为是第μ+1天的临时出行下车站点。

图3 乘客非闭环公交出行下车站点估计
通过交叉口时下车总乘客人数计算步骤如下:
Step1:输入包含IC卡编号和刷卡时刻的IC卡列表和命令;
Step2:输入线路信息和站点数据列表;
Step3:利用经纬度,定义函数Fd为两个站点之间的距离,即:
(2)
式中:re为地球半径;EA、EB分别为A、B两点的经度;WA、WB分别为A、B两点的纬度。
Step4:选择所有相同IC卡编号的记录,存储在临时列表list-C中;
Step5:对于list-C中的第i条目标记录,根据输入的上下行线路及站点信息中公交车行驶方向站点数,选择可能的下车站点,将其存储在临时列表list-D中;
Step6:利用Fd选择list-D中距离最近的站点为第i+ 1条记录的上车站点;若当前记录是同一IC卡的最后一条记录,则使用Fd选择list-D中最近的站点作为第一条记录的下车站点;
Step7:选择下一个相同记录的IC卡编号,重复Step6,直到处理完所有的IC卡编号记录;
Step8:输出带有上、下车站点信息的IC卡数据;
Step9:利用Step8得到的IC卡数据,分别统计第δ个站点的下车总乘客人数xδ;
Step10:输出通过交叉口时下车总乘客数Xd,即:
(3)
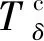
综合式(1)、式(3),可得到公交车通过交叉口时的实时载客量P为:
P=Pu-Xd
(4)
2 公交信号优先改进策略及延误
2.1 公交信号优先改进策略
传统公交信号优先一般采用绿灯延长或绿灯早启的策略。传统绿灯延长策略是指当公交车辆到达交叉口时,公交优先相位为绿灯、但剩余绿灯时间不足以让公交车通过交叉口,则将公交优先相位绿灯延长,让公交车辆通行,其绿灯延长时间由相邻非优先相位单独承担。传统绿灯早启策略是指当公交车辆到达交叉口时,公交优先相位为红灯、但即将转为绿灯,且非优先相位绿灯显示时间已超过最小绿灯时间,则将公交优先相位绿灯早启,放行公交车,其绿灯早启时间由相邻非优先相位绿灯缩短来承担。显然传统的公交信号优先策略挤占了相邻非优先相位的绿灯时间,使得相邻非优先相位车辆的运行受到了极大影响。
笔者对传统公交优先的策略进行了改进,使所有非优先相位共同承担公交信号优先相位绿灯延长的时间为ge,即改进绿灯延长策略,如图4。使所有非优先相位共同承担公交优先相位绿灯早启的时间为gs,即改进绿灯早启策略,如图5。

图4 改进绿灯延长策略相位
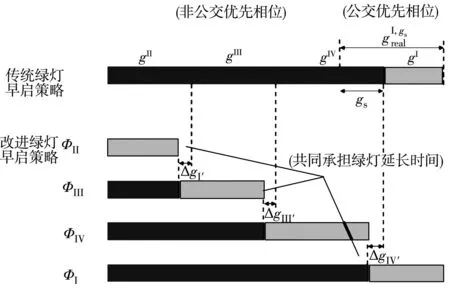
图5 改进绿灯早启策略相位
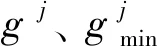
2.1.1 改进绿灯延长策略

(5)
对于传统绿灯延长策略,φI最大延长绿灯时间ge, max由相邻非优先相位φⅡ的初始绿灯时间和最小绿灯时间决定,即:
(6)
式中:ge≤ge, max。
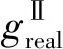
(7)
其他非优先相位φⅢ、φⅣ的实际绿灯时间不变。
对于改进绿灯延长策略,ge,max由各非优先相位的初始绿灯时间和最小绿灯时间决定,即:
(8)
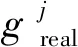
(9)
2.1.2 改进绿灯早启策略
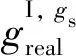
(10)
对于传统绿灯早启策略,公交优先相位绿灯最大早启时间gs, max由非优先相位φⅣ的初始绿灯时间和最小绿灯时间决定,即:
(11)
式中:gs≤gs, max。
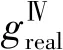
(12)
其他非优先φⅡ、φⅢ的实际绿灯时间不变。
对于改进绿灯早启策略,gs,max由各非优先相位的初始绿灯时间和最小绿灯时间决定,即:
(13)
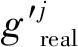
(14)
2.2 公交信号优先改进策略的车辆延误分析
2.2.1 改进绿灯延长策略的车辆延误分析
针对四相位周期的改进绿灯延长策略,车辆延误分析如图6。图6中:横轴T为时间,纵轴Q为到达交叉口排队或通过的车辆数量。在φI中,A、E点为改进绿灯延长策略起、终时刻。A点到达的公交车恰好遇上红灯无法通行,但此时在绿灯延长策略下,延长时间为ge,即AE段到达的公交车均可通过交叉口。
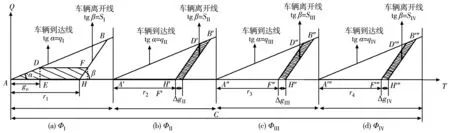
图6 改进绿灯延长策略延误分析
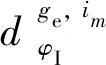
(15)
式中:sⅠ为φI的饱和流率;qⅠ为车辆到达率;r1为红灯时长。
(16)
2.2.2 改进绿灯早启策略的车辆延误分析
针对四相位周期的改进绿灯早启策略,车辆延误分析如图7。公交优先相位φI中的U、W点为改进绿灯早启策略起、终时刻,U点到达的公交车恰好遇上红灯无法通行,但此时在绿灯早启策略下,早启时间gs后UW段到达的公交车均可通过交叉口。
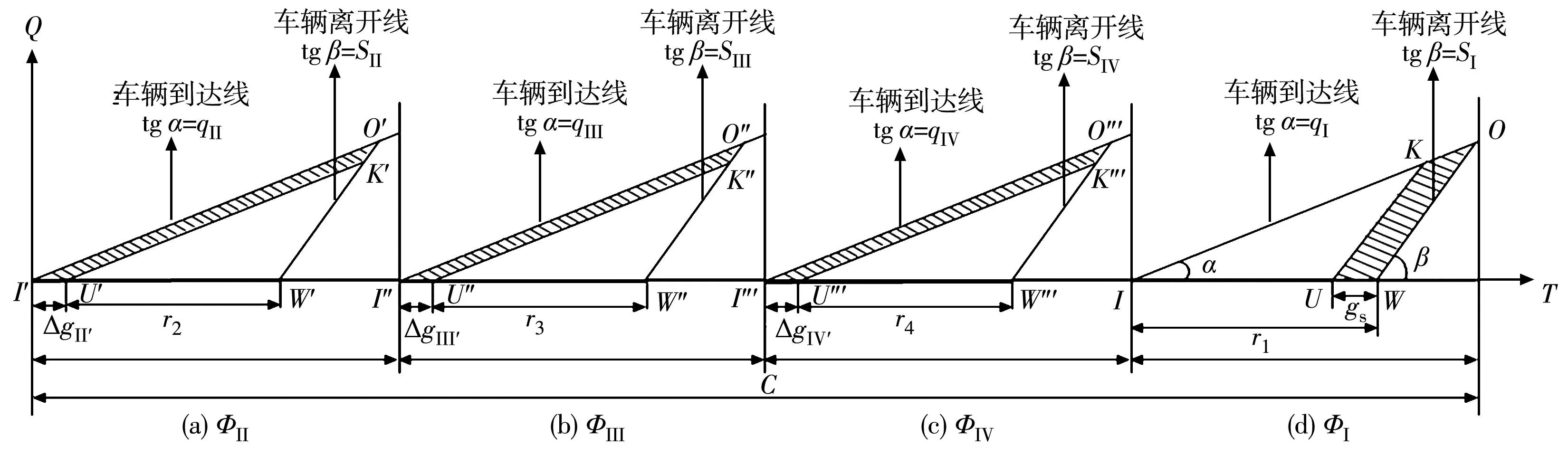
图7 改进绿灯早启策略延误分析
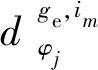
(17)
(18)
2.3 公交优先强度系数
公交车载客量远大于社会车辆,但传统延误计算模型不考虑车辆实际载客人数,只计算了车辆的延误,没计算人的延误。因此有必要在延误模型中设置一个公交优先强度系数,来描述不同载客量公交车通过交叉口时的需求强度。
在一个周期时间段C内,公交信号优先相位的所有非公交专用进口道(不含右转车道)通过社会车辆载客人数Pv为:
(19)
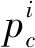
定义公交优先强度系数β为通过该方向m辆公交实时载客量之和P总和同相位内所有非公交专用进口道(不含右转车道)通过人数Pv之比,即:
(20)
P总=P1+P2+…+Pm
(21)
2.4 公交信号优先改进策略的周期延误
在改进绿灯延长或绿灯早启公交信号优先策略下,一个周期的总延误d为公交优先相位延误与所有非公交优先相位延误之和,即:
(22)
3 公交信号优先控制模型
信号控制评价指标一般用车均延误,笔者以人均延误作为评价指标,则更能体现以人为本的交通出行理念。一个周期内信号交叉口的人均延误为该周期的总延误与通过交叉口的总人数之比。公交信号优先控制优化的目标是使人均延误最小,即:
(23)
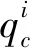
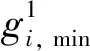
式(25)为周期时长约束,表示信号周期时长为各个相位的绿灯时长与损失时间之和。采用常用启发式搜索算法对上述公交信号优先控制模型进行求解,以绿灯早启策略为例,步骤如下:
Step1:定义参数及变量。设有n个相位,相位i的绿灯时长、红灯时长、到达率、饱和流率及绿灯早启时长分别为gi,ri,qi,si,ji;记绿灯早启调整时长为J,其中i对应其余非优先相位;定义空集合W用于存储各相位承担早启绿灯时长方案;定义空集合V用于存储各方案对应的人均最小延误;令j2,…,jn=1,则对应j1=j2+…+jn;
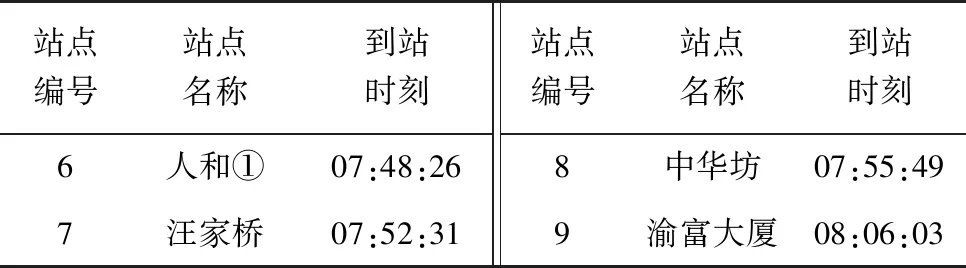
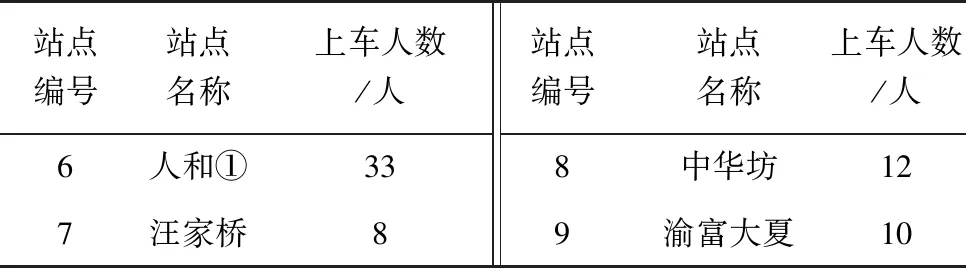
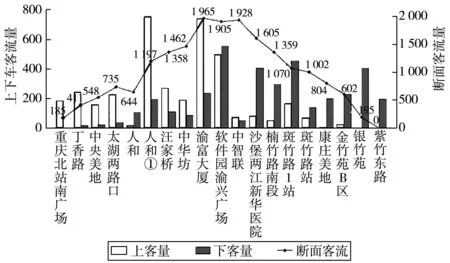
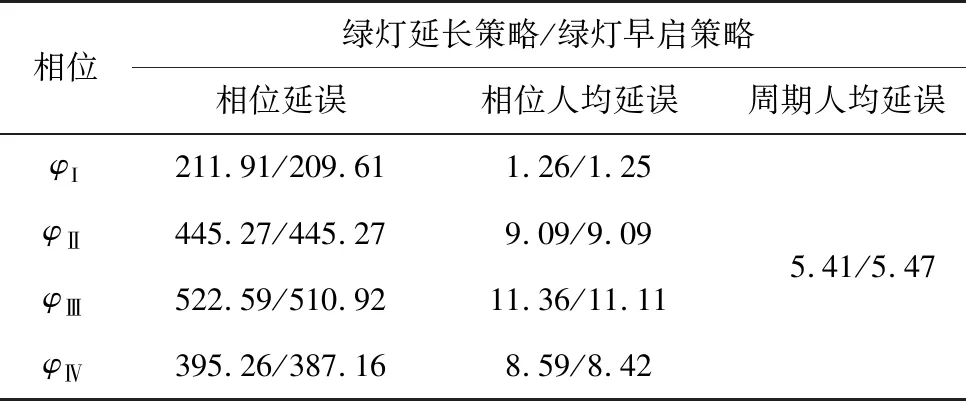
Step2:判断是否满足j1=J,j2 Step2.1:i∈[2,n],若有ji Step2.2:判断此时是否满足i Step3:最小延误索引。取集合V对应最小值Vj=min(V),各相位分担早启绿灯时长组合方案为Wj。 笔者选取重庆市某交叉口进行实例分析,如图8。该交叉口4个进口道各有4条车道,均设置了右转专用道,右转车辆通行不受信号控制,东、西进口道直行方向各设有一条公交专用道。 图8 实验场景交叉口道路渠化现状 该交叉口采用定周期信号配时,分4个相位,公交专用道车辆通行相位为φI,其他3个为非优先相位,现状信号配时方案和各进口道车流量流向如图9。 图9 交叉口信控参数和流量流向 3条公交线路(869、830、886路)由东向西通过该交叉口,其上游站点分别为8、6、13个。某日晚高峰的公交优先相位内,3条线路各有一辆公交车到达交叉口,设公交平均载客量为40人/辆,即3辆公交载客量共120人;经实地调查,并参考文献[17],社会车辆平均载客量为1.5车/人。 交叉口高峰期φI延长(早启)了绿时为6 s,满足3辆公交车通过交叉口,实测传统公交优先策略相位φI、φⅡ、φⅢ、φⅣ实际绿灯时间分别为27、27(33)、28、24(18)s。参照文献[18],得到传统公交优先策略控制方案的各相位人均延误和周期人均延误如表1。 表1 传统公交优先策略下各项延误 4.2.1 公交实时载客量分析 1)上车站点及人数对比 提取上述3路公交车某工作日早高峰的IC卡和GPS数据,经预处理后,以869路编号为82263的公交车为例,“重庆北站南广场—紫竹东路”的部分站点及到站时刻如表2。 表2 869路部分站点到站时刻 表3 869路部分站点上车人数 2)下车站点及人数推算 利用1.2节算法流程,基于乘客出行刷卡次数,将闭环公交出行定义为“多次刷卡”;将非闭环公交出行定义为“单次刷卡”。满足“多次刷卡”记录的乘客可通过下一次出行的O点反推上一次出行的D点;满足“单次刷卡”记录的乘客,可通过不同日期同一公交线路的“多次出行”上车站点记录,推算仅有“单次刷卡”下车站点。 3)实时载客量及线路OD图分析 图10 869路公交车早高峰OD关系 4.2.2 基于实时载客量的各项延误计算 根据文献[19],笔者取直行车道的饱和流率为1 800 pcu/h,左转车道的饱和流率为1 550 pcu/h。对于4相位单点信控交叉口采用改进绿灯延长策略,经实地测得该信号周期总损失时间为L=13 s,由式(24)可得到现状信号方案的3个非公交优先相位(φⅡ、φⅢ、φⅣ)的最小绿灯时间分别为18、22、15 s;改进绿灯早启策略的3个非公交优先相位(φⅡ、φⅢ、φⅣ)的最小绿灯时间分别为20、20、17 s。 用启发式算法计算出的各相位最优绿灯时间可得:最小周期总延误d和交叉口最小人均总延误,将各参数代入式(23)可得到目标函数表达为: (26) 针对单个周期的一个公交优先相位,采用改进绿灯延长、改进绿灯早启,延长(早启)至少10 s(8 s)绿灯时间,才能使公交车辆不停车通过交叉口,则取最小绿灯延长(绿灯早启)时间为10 s(8 s)。改进策略各相位绿灯时间变化量如表4,各相位人均延误与周期人均延误如表5。 表4 改进公交信号策略下各相位绿灯时间变化量 表5 改进公交优先策略下各项延误 由表4、表5可知:基于公交车实时载客量,采用改进的绿灯延长、绿灯早启公交信号优先控制策略,交叉口周期人均延误较于传统公交信号优先策略分别降低了1.43、1.24 s,降低幅度分别为20.98%、18.11%。 笔者利用公交IC卡和GPS数据,对乘客上下车站点进行分析,得到了公交车通过交叉口时的实时载客量;分析了改进绿灯延长和绿灯早启交叉口各相位车辆的延误,引入了公交优先强度系数,综合公交实时载客量和社会车辆驾乘人员,以通过交叉口所有人员的人均延误最小为目标,构建了公交信号优先控制模型。 以重庆市某交叉口为例进行分析。结果表明:基于公交车实时载客量,采用改进的绿灯延长和绿灯早启策略相较于传统公交信号优先策略,交叉口周期人均延误分别降低了1.43、1.24 s,降低幅度分别为20.98%、18.11%。4 实例应用分析

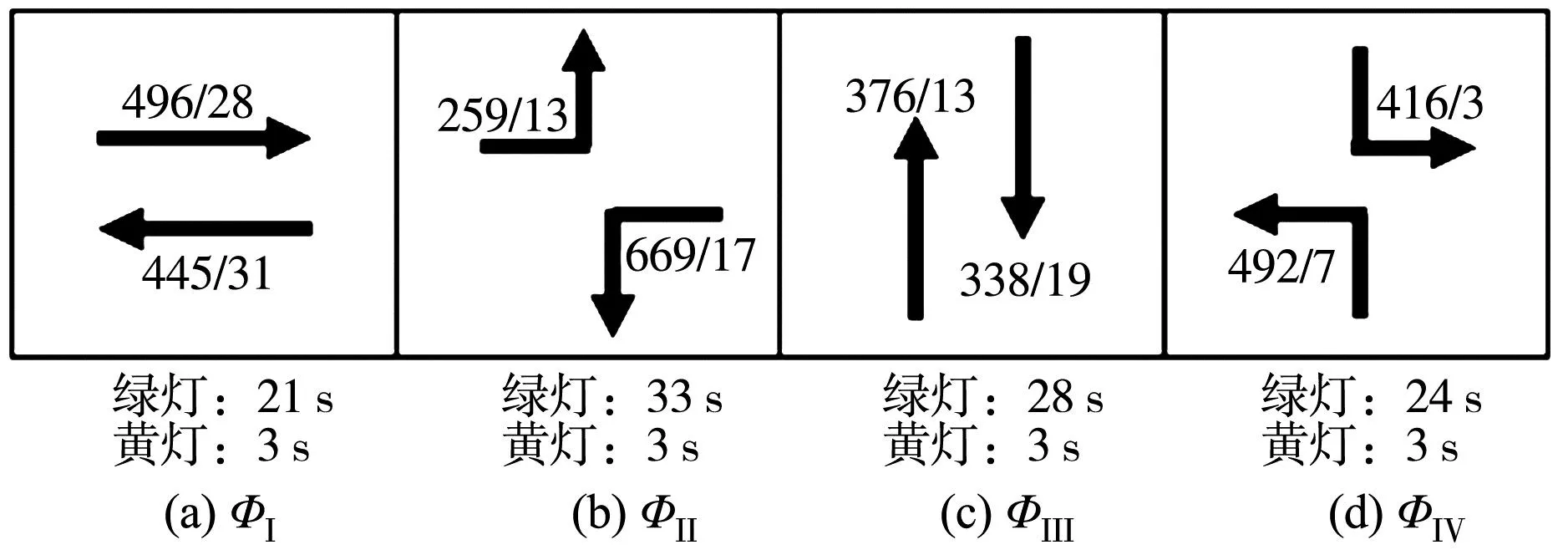
4.1 传统公交优先策略控制方案
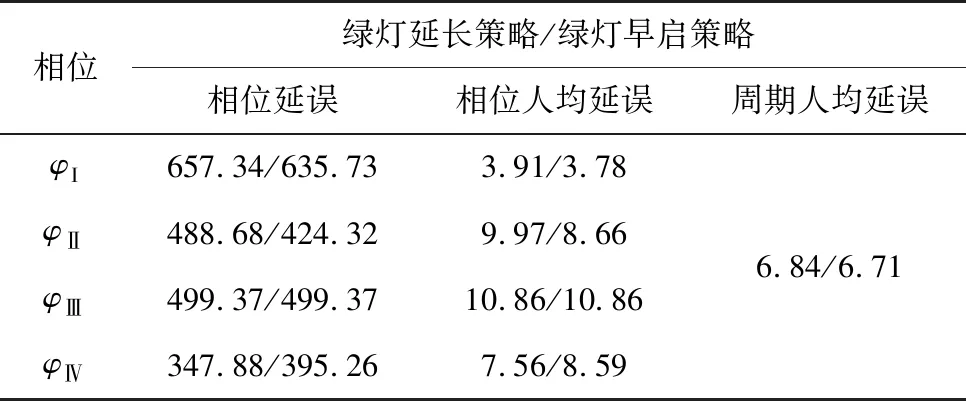
4.2 改进公交优先策略控制方案
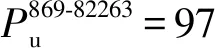
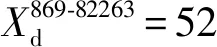
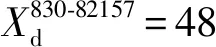

5 结 语

