永磁同步电机无加权因子的模型预测控制

祖 冉，黄妍慧，李 敏

（安徽机电职业技术学院，安徽 芜湖 241002）

模型预测控制（MPC）是一种新兴的电力驱动和电力电子非线性控制技术［1］。与传统的线性控制器相比，它用非线性控制器代替了内部PI 电流控制器，使电流控制带宽无限大［2-4］。根据输出电压的特性，MPC 可分为两类：连续MPC（CMPC）和有限控制状态MPC（FCS-MPC）［5］。CMPC 以分析的方式计算参考电压，从而可以获得连续的参考电压矢量和固定的开关频率。但其实现过程复杂，并且消耗相对较大的计算时间［6-7］。FCS-MPC 属于电力驱动的直接控制策略，无需PWM 模块，通过评价函数从一组固定的电压源逆变器选择可用的参考电压［8］。FCS-MPC可进一步分为预测电流控制（PCC）及其增强形式预测转矩控制（PTC）［9-10］。与PCC 相比，PTC以加权因子形式或其他非线性方式单独控制转矩和磁通量，例如通过排序和模糊逻辑或将多个控制项集成为一个，甚至通过基于图形优化的方法试图消除加权因子的影响［11-12］。文献［13］提出了一种简单的无加权因子顺序预测转矩控制（SPTC），然而它的评价函数执行顺序是固定的，这可能导致不同计算点的非最优解。本研究在文献［11］的基础上，引入了用于评价函数计算改进的变序列SPTC。

内置式永磁同步电机（IPMSM）不仅具有高转矩密度和高效率，而且具有转子结构简单、机械强度高、制造成本低和惯性小等优点［14］，具有更高的气隙磁通密度使其更适合于弱磁控制［15］。基于这些优点，本研究以IPMSM 为研究对象来验证无加权因子的模型预测控制的有效性。

1 控制对象及其模型

1.1 积电压源逆变器

电源通过电压源逆变器（VSI）从直流电源转换得来。在本研究中，为了简化验证，采用最常见的3 相和2 级VSI，如图1 所示。

图1 逆变器电路和电压矢量Fig.1 Circuit and voltage vectors of VSI

每个状态的积分电压矢量V可以表示为

式中，Vdc是直流电压源；a=ej2π/3；Sa、Sb、Sc指的是每个支路的开关状态。由于存在8 种不同开关状态组合，因此存在7 种不同的可行电压矢量，不包括零矢量。

1.2 IPMSM 数学模型

在定子静止坐标系下，IPMSM 的数学模型矢量表达式为

为了便于推导，在转子同步参考系中，定子电压和定子磁链进一步以标量分量形式表示，

式中，ωe表示电角速度；ψd、ψq分别表示d、q轴的磁链；Ld、Lq分别表示d、q轴的电感矢量。电磁转矩（Te）可以写成：

式中，P表示极对数。

2 无加权因子PTC

2.1 传统的PTC

通过对转矩和定子磁链的预测，可以得到最佳参考电压矢量，定子电流作为中间变量也会被预测。通常，为了计算简单，以数字方式来表达公式，将连续状态方程转换为离散状态方程。根据式（2），定子磁链可预测为

定子电流可预测为

式（5）和式（6）中，k和k+1 分别表示当前和下一个周期的变量。

由于最优电压矢量不能在同一控制周期内施加，因此需要进行时间补偿以保证控制精度。磁链预测为

为了简化计算，将磁链的预测公式转换到同步参考系，即

根据式（3），在同步坐标系中，预测电流可以写成：

预测电磁转矩为

为了实现对转矩和磁链以及其他非线性量或约束的均匀控制，设计了具有最小两项的评价函数：

2.2 无加权因子控制策略

相比于传统控制中所有组合使用单个评价函数，无加权因子控制策略利用评价函数的单独级联方式，通过消除评价函数中的加权因子来简化控制。图2 是改进的控制系统示意图。

图2 控制系统框图Fig.2 Control system block diagram

在该控制系统中有两个单独的评价函数，即转矩gT和定子磁链gψ，即

与传统的PTC 类似，首先预测定子磁链和转矩。但是该方法不再将7 个电压矢量替换为单个评价函数，而是这些电压矢量首先由上述两个评价函数之一进行计算。根据当前周期中控制目标的优先级和不同的机器特征，从7 个电压矢量中选择合适的电压矢量计算得到最小（即最佳）评价函数值，并且将所选择的矢量作为一组有限的可行电压矢量，提供给另一个评价函数。最终选择最小化的第二个评价函数的电压矢量作为全局优化的电压矢量，其相应的开关状态被发送到逆变器。

通过跟踪和误差的方式选择最佳电压矢量的数量，可以在计算量和控制对象的重要性之间取得平衡。理论上第二个评价函数选择的矢量越少，第一个评价函数的控制对象就越重要。因此，在本研究中，从第一个评价函数中选择最佳的3 个电压矢量，并将其提供给第二个评价函数。在这种情况下，首先被计算的评价函数的控制对象就更为重要。

此外，为了避免因为提高系统精度和动态性而造成对任一控制对象（即转矩和定子磁链）的控制失衡，可以基于先前评价函数值来进行序列选择。这些值用作决策查找表（LUT）的输入，该表决定在每个控制周期中首先计算哪个评价函数。其基本原理是控制对象在上一个控制周期内的评价函数最小值越大，其评价函数在下一个控制期内被首次计算的可能性就越大。

在所提出的系统中，当稳态时，通过设置λ=Nnom/(ψpmLd)，就能够确定每个控制对象的评价函数值的范围。因此，可以用合理的方式设计LUT 的阈值。LUT 如表1 所示，其中转矩和磁链的阈值分别为ΔgT和Δgψ。如表1 和图2 所示，LUT 作为连接不同评价函数序列的两个互补开关来执行。

表1 评价函数执行序列决策LUTTab.1 Evaluation function executive sequence decision-making LUT

3 实验验证

3.1 平台介绍

图3 是3.6 kW 永磁同步电机的控制系统实验平台，采样频率为10 kHz。表2 是电机的参数。

表2 电机参数Tab.2 Motor parameters

图3 实验平台Fig.3 Experimental platform

首先对传统的PTC 进行初始化测试，以确定IPMSM 在其稳定状态下以额定速度和转矩运行时LUT 的阈值。转矩和磁链的标准偏差分别为0.15 Nm 和0.04 Wb。因此，设置ΔgT=0.15 Nm和Δgψ=0.04 Wb 是合理的。为了更好地评估，在模拟中比较了传统的PTC 和提出的SPTC 的性能。

3.2 实验结果分析

PTC 和SPTC 的动态性能比较如图4 和图5 所示。从上到下依次为转子速度、电磁转矩、磁链和三相电流。速度指令在0.8 s 时从2 772 r/min 切换为-2 772 r/min。对于两个系统来说，转子速度可以在0.6 s 内跟踪其参考值。可以看出，所提出的SPTC 比传统的PTC 具有更加优异的动态性能。与PTC 相比，SPTC 具有更低的定子电流谐波和电磁转矩脉动。此外，在所提出的系统中，定子磁链的波动略大。但是由于磁通只是中间项，其值不会直接影响系统性能和指数，只要转矩、速度以及电流得到良好控制，其变化就可以忽略。每个步骤的成本函数执行的优先级如图6 所示，其中0 代表gT应首先计算，1 代表gψ应首先计算。从图6 可以看出，顺序频繁交替，在速度反转的瞬间，扭矩依然能够被很好地控制。

图4 PTC 动态特性Fig.4 Dynamic-state performance of PTC

图5 SPTC 动态特性Fig.5 Dynamic-state performance of SPTC

图6 SPTC 正反转执行序列Fig.6 SPTC forward and reverse execution sequence

PTC 和SPTC 的瞬态性能如图7 和图8 所示。电机以扭矩模式运行。电磁转矩指令在3.5 ms时从0 变化为7.5 Nm。从上到下依次为转子速度、电磁转矩、磁链和三相电流。可以看出，尽管负载有变化，但磁链仍然趋于稳定，两个系统都可以立即平衡负载，几乎没有时间延迟，速度变化也很轻微。PTC 的电磁转矩响应时间为1 000 μs，而SPTC 的响应时间为860 μs。图中，开关状态0 表示000，6 表示110。

图7 PTC 瞬态特性Fig.7 Transient performance of PTC

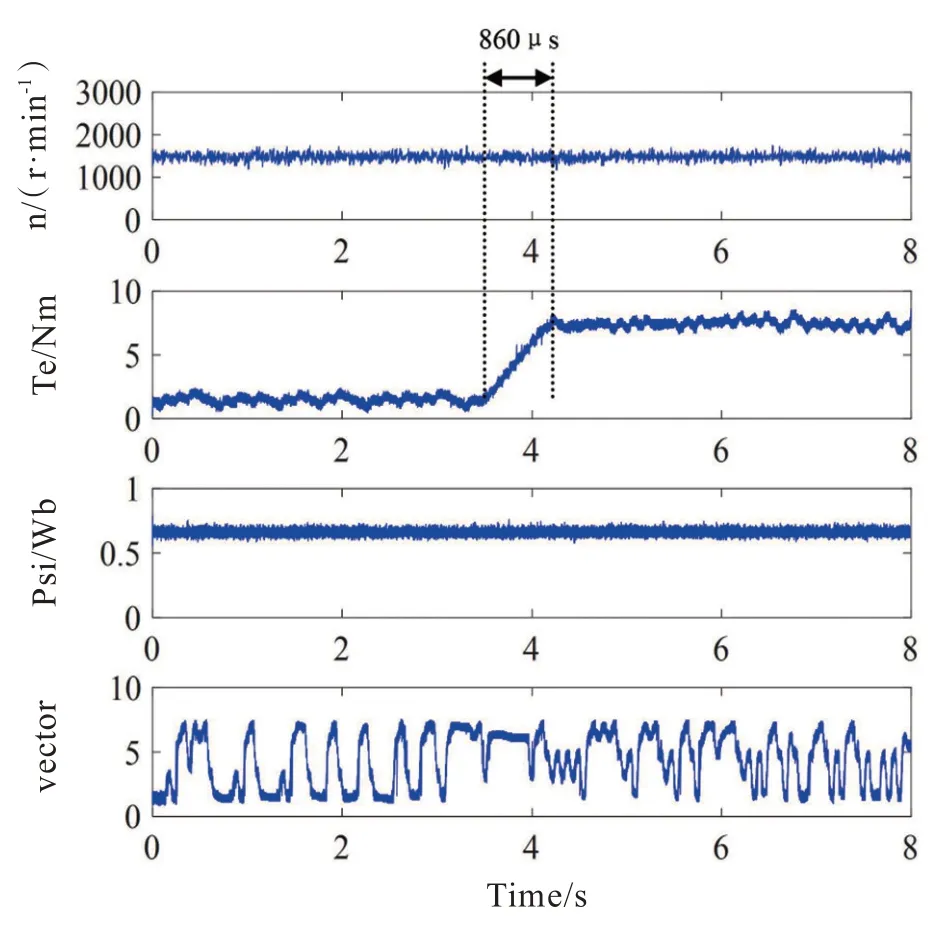
图8 SPTC 瞬态特性Fig.8 Transient performance of SPTC

PTC 和SPTC 的稳态性能比较如图9 和图10 所示。可以看出，所提出的SPTC 具有更优异的稳态性能。SPTC 的定子电流THD 为9.86%，比传统的PTC 低20.29%。SPTC 的电磁转矩脉动为1.0 Nm，比传统的PTC 低50%。

图9 PTC 稳态特性Fig.9 Steady-state performance of PTC

图10 SPTC 稳态特性Fig.10 Steady-state performance of SPTC

PTC 和SPTC 的跟踪能力如图11 和图12 所示。可以看出，当电机给定转矩发生突变时，PTC 和SPTC 的响应都很快，转矩和d轴电流都能无差地跟踪到给定值，且没有相互耦合和超调的现象。PTC 的响应时间为760 μs，SPTC 的响应时间为570 μs。研究发现，这两种系统都具有快速的误差收敛和精确的跟踪性能。

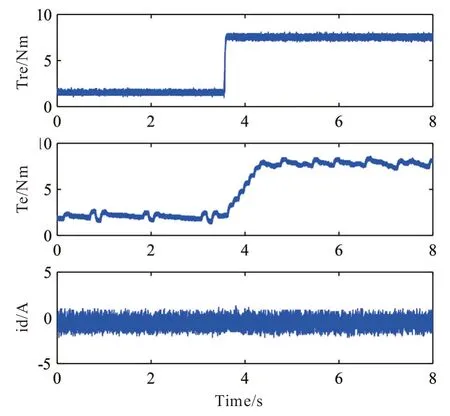
图11 PTC 跟踪特性Fig.11 Tracking-performance of PTC

上述实验结果与理论推导是相吻合的，与传统的PTC 相比，SPTC 控制更为简单，性能更加优异。表明本研究中提出的控制策略是可行且有效的。

4 结语

本文提出了一种用于电机预测转矩和磁链控制的无加权因子评价函数控制策略。实验结果表明，该策略与传统的PTC 相比，效果相似且稍好，能够保持传统的PTC 的快速动态响应的优点，且不需要调整加权因子，是传统方法的理想替代方案。此外，评价函数中的可变控制序列使系统能够适应更宽的带宽范围。通过改变阈值作为评价函数执行序列决策LUT 中的标准，仍然可以对具有权重系数的传统MPC 进行调整。该策略可以大大降低多目标预测控制系统设计的复杂性。