去中心跨孤岛的混合联邦学习通信算法研究

吴明奇,康 健,李 强

(吉林大学 计算机科学与技术学院,长春 130012)

0 引 言

随着人类收集、存储、计算、处理数据能力的飞速发展,亟需高效的对数据进行分析利用的算法。机器学习以其擅长分析处理大量数据的特点,在银行和金融机构的风险评估和广告投递分析应用中得到了广泛应用[1-2]。但其在金融数据中的应用同时引发了诸多隐私保护问题,尤其是在多个银行共同训练一个机器学习模型的多方机器学习中,用户账户的敏感数据通常在模型聚合和传输阶段暴露,随着用户对个人隐私数据的保护意识逐渐增强,如何高效、安全、可靠的开展多方机器学习成为了目前亟待解决的问题。

联邦学习是用于解决多方机器学习安全问题的主要方式之一。其核心思想是数据不离开本地,并在本地进行局部迭代,通常上传到云端的是经过加密的模型参数,从而达到既保护数据隐私,又能共同训练机器学习模型的目的。目前现有技术的联邦学习运营模式基本是每个参与方在本地进行局部模型训练,然后将模型上传给中央服务器,再由中央服务器进行聚合分发。

由于现有公开技术的联邦学习是针对特征维度相同的数据样本进行训练,通常称之为横向联邦学习,也有技术针对特征维度不同的纵向联邦学习进行研究,但大部分纵向方法因为使用了同态加密方案,计算开销较大。而纵向与横向联邦学习的区别不仅在于数据分布的方式,并且特征的分散导致纵向联邦学习的训练计算方式与传统机器学习和横向联邦学习有很大区别。

联邦学习的场景还分为大量移动设备的跨设备联邦学习,和以数据孤岛为主体的跨silo联邦学习[3]。然而跨silo联邦学习与传统跨设备联邦学习的场景条件有所不同,跨silo不需考虑客户端退出的影响和大量设备沟通的瓶颈问题,而需要考虑更多计算和通信瓶颈的问题。

基于上述可知,虽然现有技术能实现特征维度不同参与方的纵向联邦学习通信,但横纵混合的联邦学习方案仍有待研究。其相比传统联邦学习具有更高的兼容性,能满足大多数联邦学习场景的需求,如金融场景下环球同业银行金融电讯协会和其州子银行进行的异构横纵混合联邦学习,医疗场景下不同医院、科室进行的疾病判断联邦学习。但横纵混合跨silo场景面临着纵向同态加密计算瓶颈导致的横纵计算不一致问题。如何实现一个高效的横纵混合联邦学习算法并在此基础上实现分散去中心化是当前联邦学习领域亟待解决的问题。

针对上述问题,笔者提出了分层混合通信算法:1) 实现了拥有不同数据分区方式的参与方之间进行联邦学习通信; 2) 采用去中心思路,消除了可信第三方中心聚合器的影响; 3) 采用分层交互方法和一种伪中心的思路实现纵向分区的联邦学习; 4) 通过增加本地迭代轮次,降低了silos之前间的巨大计算瓶颈。

1 相关工作

联邦学习起始概念是通过聚合本地的梯度训练机器学习模型,而不需要将分布的数据集集中在同一个设备上[3]。目前针对联邦学习的研究,数据主要在多个客户端之间呈水平划分,其中联邦平均算法得到了广泛研究。其相关工作主要分为3类[4]:对横向数据分区的联邦学习进行去中心化操作; 对网络拓扑结构进行分层或分簇进行联邦学习; 以及对纵向数据分区的联邦学习进行研究。

横向去中心化联邦学习的研究现状如下:其最早研究应用于google输入法预测,因此对其研究场景主要是边缘分布式设备。有研究表明分散梯度下降可以达到与集中式计算相当的收敛速度,并且通信较少。分散学习算法主要分为固定网络拓扑和拓扑随迭代动态改变[5-6]。He等[7]和Hu等[8]提供了分散联邦学习的实现参考和系统分析。当前横向去中心化联邦学习的研究主要应用于跨设备场景,而笔者考虑了跨silo的联邦学习场景。

分层联邦学习的研究现状如下:分层联邦学习通常采用基站-设备的方式对边缘设备客户端进行分层以达到提高计算效率减小通信开销的目的[9]。Roy[10]分析了水平数据分区的分层联邦学习。Liu等[11]采用分簇的方式处理非独立同分布数据,Castiglia等[12]探讨了顶层垂直分布的分层联邦学习设置。

纵向联邦学习的研究现状如下:Chen等[13]提出了单层网络通信中的垂直联邦学习算法。Wei等[14]使用同态加密等方式消除了中心聚合服务器的影响,但仍是在垂直的单层网络中进行联邦学习。而笔者考虑了在两个层中同时处理水平和垂直分区并且不采用中央聚合服务器。

2 技术支持及问题设置

2.1 技术支持

2.1.1 逻辑回归

通过逻辑回归sigmoid激活函数,训练了一个线性模型W,其将实例X映射到一个二元标签y∈[0,1],回归函数模型为

(1)

其中x1,x2,…,xn为数据特征,w0,w1,…,wn为模型参数。

在二进制分类问题中,假设阈值为0.5,输出大于阈值分类为正结果,输出小于阈值输出为负结果。使用随机梯度下降法对参数模型进行优化,为表示真实标签与预测结果的误差程度,需要计算交叉熵损失函数,优化的平均逻辑损失为

(2)

其中K为数据集中样本数,y*为标签的真实值,h由式(1)计算得出。

为了使损失函数收敛,需要求出损失函数梯度下降的方向,其公式为

(3)

最后损失函数收敛,梯度下降优化完成,从而完成训练过程。最终的参数W为结果参数。在联邦学习中,参与方传递的只有模型参数W的相关信息,本地数据X只参与计算,不向其他客户端传递。

2.1.2 同态加密

同态加密提供了一种密码学加密方案[15]。该算法使客户端可以对数据加密后发送给第三方,第三方能在加密的密文数据上完成特定运算f,而不获取数据的明文信息,客户端收到加密运算的结果后解密,与在明文上进行运算f的结果一致,笔者采用的f运算如下:

[[a]]+[[b]]=[[a+b]],a[[b]]=[[ab]],

(4)

其中[[x]]为x的密文。

2.2 系统模型及问题设置

笔者考虑一个由N个silos组成的分散系统,如图1所示。其中每个silo由一个数据水平分布的客户端或一组数据纵向分布的客户端组成。

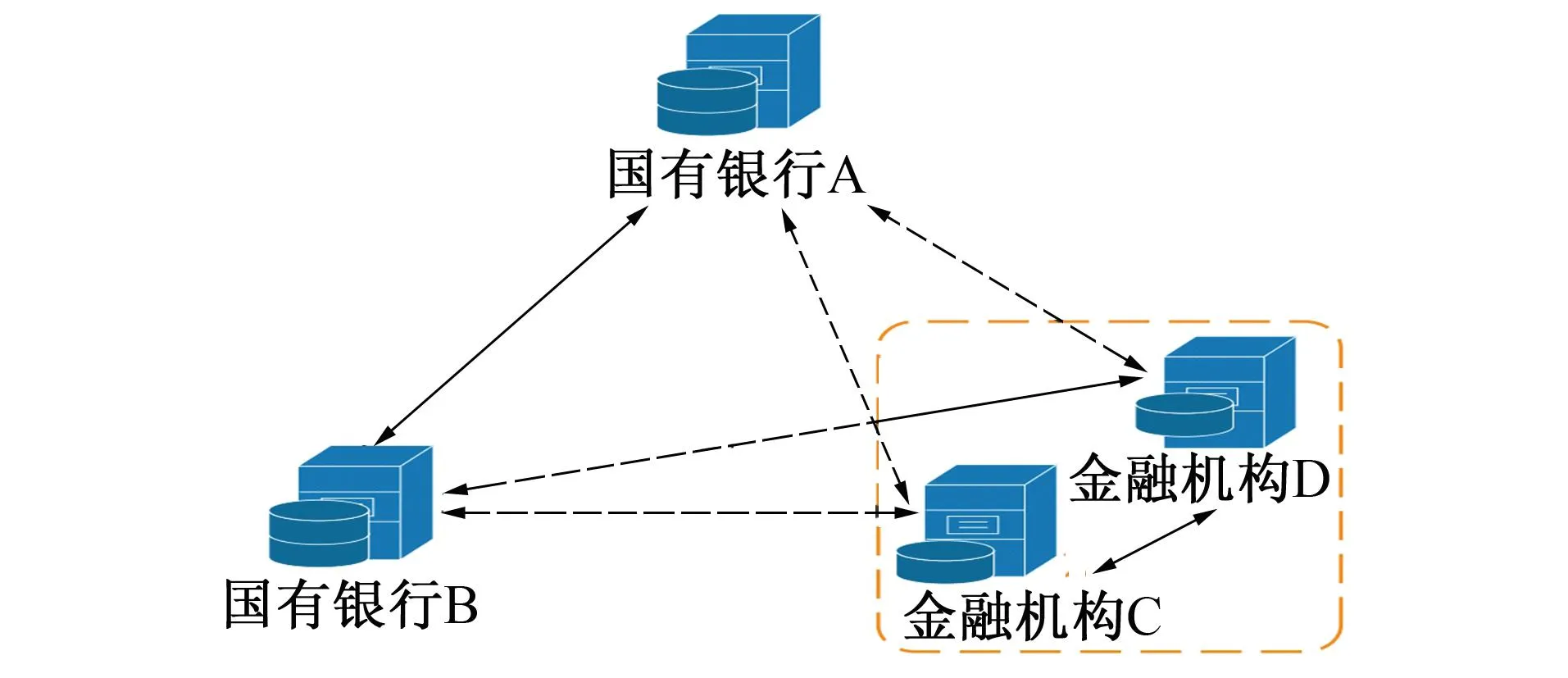
图1 一个cross-silo模型架构

文中的网络分为两层:水平分散分布的顶层,垂直分布的底层,从而形成了一个包含垂直和水平数据分区的联邦学习通信网络。

3 分散混合联邦通信算法

跨silo场景同时拥有水平和垂直silo,为解决不同数据分区silos间的交互问题,交流过程可分成两层3部分实现。纵向silo内的交互采用底层纵向交互算法; 横向silos间的交互采用顶层横向交互算法; 横向和纵向silo的交互采用顶层横纵交互算法。

3.1 顶层横向交互算法

顶层横向客户端交互算法执行流程如图2所示。各横向silos持有完整的局部模型,采用广播方式实现去中心的水平联邦学习过程。算法1给出了顶层横向交互算法伪代码。

图2 顶层横向交互算法的执行流程

算法1 顶层横向交互算法。

Require:learning ratelr,number of iterationsT,number of top partyN

1) InitializeNparties models,W={W1,…,Wn} with random weights

2) Fort=0,1,…,T-1 do

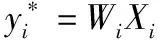
5) computesD=δL/δWi

6) updateWi=Wi-lrD

7) sendWijto allj∈Niout,Viout

8) receiveWjifrom allj∈Niout

9)Wi=∑Wki/N

10) End For

在顶层算法中假设N个数据水平分布的横向参与者,其样本特征维度重合但ID不同。参与方i持有的数据为Xi,对应的权重为Wi。

第1步 第1行,进行初始化操作,初始化N个参与方的模型并随机生成权重W1,…,Wn。

第2步 第3～6行,对每个参与方使用本地的数据计算loss和梯度D,得到本地局部模型。

第3步 第7行,每个参与方将本地局部模型Wij广播给其他参与方j。

第4步 第8～9行,参与方i对所有接收到的模型Wki聚合平均得到全局模型Wi,并更新本地模型。返回第2步直至达到迭代轮次。

3.2 底层纵向交互算法

底层纵向客户端交互算法如图3所示。纵向参与方持有的特征维度不同,各方通过各自训练对应自己特征维度的模型并通过同态加密传递中间参数完成训练过程。同时不需要可信第三方执行伪中心的工作。算法2给出了底层纵向交互算法伪代码。

图3 底层纵向交互算法的执行流程

算法2 底层纵向交互算法。

Require:learning ratelr,number of iterationsT

1)Arandom initializeWaandVb,generates PRIaand PUBa,Asend PUBatoB,Brandom initializeWband receive PUBa

2) Fort=0,1,…,T-1 do

3) Forq=0,1,…,Q-1 do

4)Acomputesy*=WaXa+Vb

5)Acomputes lossLbyy*

6)AcomputesDa=δL/δWi

7)AupdateWa=Wa-lrDa

8) End For

9)Aencrtpts SUM(yi-y*) use PRIaand send it toB

10)Breceive[[SUM(y-y*)]]and computes[[Db]]=[[δL/δWb]]

11)Bsend[[Db]]+[[Rb]]toA

12)Areceive[[Db]]+[[Rb]]decrypts it and send the plaintext toB

13)Bget plaintextDb+Rband computesDb

14)BupdateWb=Wb-lrDb

15)BcomputesWbXband send toA

16)AupdateVb=WbX

17) End For

在底层算法中假设A和B为两个纵向参与者,A和B的样本ID重合但特征维度不同,特征维度由m,n表示,数据的标签仅被一方持有。A保存的数据为Xa=(xa1,xa2,…,xam)及标签y,B持有的数据为Xb=(xb1,xb2,…,xbn)。A和B对应的权重分别为Wa和Wb。

第1步,第1行进行初始化操作,A和B初始化权重Wa和Wb,A生成同态加密算法的公钥PUBa和私钥PRIa,并将公钥发给B。同时A初始化与B进行数据交换的分段值Vb。因为标签由A持有,因此为保证标签的保密性,秘钥由A生成,A也自然成为了该silo中的伪中心。

在第2步,第3～8行中,A使用本地数据Xa,权重Wa和分段值Vb进行q轮迭代并更新本地模型。q的作用是提高协议效率和提升训练效果,通过将epoch在一个局部迭代中完成,大幅减少加同态密和数据传输的计算量和计算时间,以提高训练效率。

第3步,第9～12行中,A使用paillier同态加密将[[y-y*]]发送给B,B应用同态加密性质计算出梯度[[Db]]并通过秘密共享与A再进行一轮交互,最终B得到梯度Db。

第4步,第13～15行中,B使用本地数据Xb,权重Wb,梯度Db更新本地模型,并计算分段值Vb发给A。

第5步,第15行中,A更新分段值Vb,并返回第2步直至达到迭代轮次。

特别地,要注意Vb和参与方A的数据对齐问题。在第1轮迭代,Xa1对应随机初始化的Vb,参与方B使用Xb1计算出Vb后参与方A需要将Vb更新,至此才算完成中间值Vb的初始化,迭代才从Xa1开始。

3.3 顶层横纵交互算法

顶层横纵客户端交互算法如图4所示。该算法给出了ID和特征均不同情况下横纵向silo的交互过程,横向silo需要拆分模型与纵向silo对齐完成联邦学习训练。算法3给出了顶层横纵交互算法伪代码。

图4 顶层横纵交互算法的执行流程

算法3 顶层横纵交互算法。

Require:learning ratelr,number of iterationsT,number of top partyN

1) InitializeNparties models,W={W1,…,Wn} with random weights

2) Fort=0,1,…,T-1 do

3)IpartitionWitoWaandWb

4)IsendWatoA

5)IsendWbtoB

6)AupdateWa=∑Wi/N

7)BupdateWb=∑Wi/N

8)AandBdo algorithm 2

9)AsendWatoI

10)BsendWbtoI

11)IaggregateWaandWbtoWi

12) End For

在顶层横纵交互算法中假设A和B为两个纵向参与者,参与方i为与之交互的横向参与者,A和B的样本数据呈垂直分布,参与方i与A,B组成的silo的样本数据呈水平分布。A保存的数据为Xa=(xa1,xa2,…,xam)及标签y,B持有的数据为Xb=(xb1,xb2,…,xbn),参与方i持有的数据为Xi=(xi1,xi2,…,xim+n)及标签y,m,n表示纵向客户端的数据维度。A和B对应的权重分别为Wa和Wb,参与方i的权重为Wi。

第1步,第1行,进行初始化操作,初始化各客户端的权重。

第2步,第3行,客户端i根据纵向客户端的维度m,n将Wi分为Wa和Wb,并将对应的权重发送给A和B。

第3步,第4行,A和B对接收到的模型Wa/Wb聚合平均得到全局模型中自己对应特征维度的模型Wa/Wb。

第4步,第5行,A,B通过算法2对本地模型进行更新。

第5步,第6行,A,B向水平参与方i广播更新后的特征维度。

第6步,第7行,水平silos将A,B的特征维度组合成完整模型并聚合得到纵向silo的局部模型。返回第2步,直至达到迭代轮次。

4 实验及结果

4.1 实验设置

实验在一台两个GPU显卡的机器上运行,参与者都部署在同一个局域网内。实现软件版本为Python 3.7.0,PyTorch 1.2.0,同态加密使用Hwlib库中的CKSS(Cheon-Kim-Song scheme)方案部署。

实验在一个真实世界的数据集上运行:SUSY(Supersymmetry Particles) 是一个大规模的二分类数据集,包含5 000 000个样本,共有18个特征维度。实验模型结构如图1所示。假设每个silo的数据量相等,权重相同。将SUSY以流数据的形式均匀分配给每个silos。

4.2 实验结果

4.2.1 算法比较

对比分层横纵联邦算法与传统集中式算法,分散和纵向梯度下降算法的性能。将集中式算法和纵向梯度下降算法设置为一个单独的silo,分散梯度下降算法设置成3个横向silos,分层横纵联邦算法设置为两个水平silo,一个垂直silo。设置训练参数为Lr=0.01,epoch=3,q=1。图5和图6给出了各算法的收敛曲线和准确率曲线,Y轴给出平均损失和准确率,X轴给出迭代次数,表1给出了各算法的最终平均准确率。从中可看出:1) 模型都能在多次迭代后快速收敛到稳定状态; 2) 横向分散式梯度下降算法相比集中式算法几乎没有性能损失; 3) 引入纵向silo会导致模型最终损失值偏高; 4) 分散横纵联邦算法和纵向梯度下降算法在迭代前期损失波动较大,但最终都趋于稳定并达到收敛状态; 5) 纵向梯度下降算法准确率波动较大,但分散横纵联邦算法中的纵向客户端准确率收敛稳定。

图5 算法准确率曲线

图6 算法收敛曲线

4.2.2 加密效率

笔者在分散横纵联邦算法中讨论局部迭代轮次q对加密效率的提升以及对模型精度的影响,并对比了算法在密文与明文下的计算时间。设置训练参数为Lr=0.01,Epoch=10。同态加密的主要计算开销集中在算法2中10～11步的大数加密和解密运算中,增加q主要是通过减少随机数Rb的加密时间和减少解密[[Db]]+[[Rb]]的工作量(这两者可以总结为对参与方B梯度的加密处理)提高训练效率。图7a给出了q取不同值时对算法性能的影响,Y轴给出平均损失Loss,X轴给出迭代次数,表2给出了各算法的最终平均准确率。图7b给出了q取不同值时算法的平均执行时间,对比了算法在明文上和在密文上的计算效率。可以看出增加局部迭代轮次会使模型loss升高,但最终仍达到收敛,并且小幅降低了模型准确率,但计算效率大幅提升,因此可以通过提高q降低纵向silo计算瓶颈。

表2 本地迭代轮次准确率表

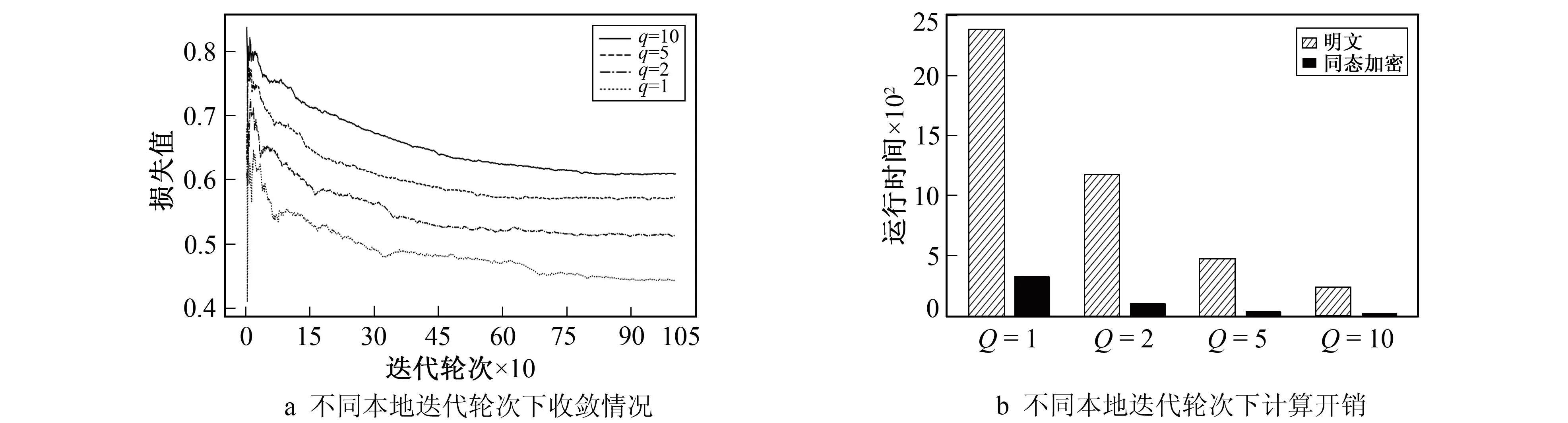
图7 本地迭代轮次效果对比

5 结 语

笔者提出了一种在同时有横向和纵向多方参与下完成逻辑回归训练且不依赖中心聚合器的分层交互方法。采用梯度共享传递silos间信息,并利用同态加密技术保护silos的隐私,同时降低了纵向客户端的加密开销。实验结果表明,分散横纵联邦算法可以很好地实现在跨silo无中心节点场景下横向和纵向silos的交互,且几乎不损失模型精度。在未来的工作中,我们将探索纵向silo加密计算瓶颈的解决方案,并研究在恶意敌手模型下如何保证协议的安全性。