四容水箱实验装置设计及其分散内模控制

于树友,谭 丽,2,曹瑞丽,侯成玉

(1.吉林大学 通信工程学院,长春 130012; 2.长春大学 电子信息工程学院,长春 130022)

0 引 言

多容水箱系统作为实验室典型的过程控制对象,不仅可为自动化专业学生提供一个开放的实践平台,同时也可用于验证先进控制算法,为科研人员提供算法验证平台。多容水箱包括垂直或水平排列的两容水箱、垂直或水平排列的三容水箱、四容水箱等[1]。其中四容水箱是具有时滞、非线性、耦合等特性的多输入多输出系统,而工业生产过程中的许多被控对象都可以抽象成四容水箱系统的数学模型[2],因此将四容水箱实验系统应用于自动控制相关课程的实验教学中,可以帮助学生更好地了解控制系统建模、掌握控制器设计等理论知识。

目前已有许多科研人员利用多容水箱进行了先进算法的验证,如预测控制[3-5]、模糊控制[6]、自抗扰控制[7]和解耦控制[8-9]等。贺宇[2]基于四容水箱的最小相位系统结构设计了一种部分分散控制器,仿真结果表明,这种控制器具有与集中控制相近的效果,且控制结构简单。Bamimore等[3]采用两种人工神经网络方法,对三容水箱进行建模与预测控制,结果表明,模糊神经网络在调节时间上优于传统神经网络。贺宇等[5]对双容水箱采用多模型自适应预测控制方法,并对其进行了仿真,仿真结果验证,与单模型相比多模型的响应速度更快,具有更好的性能。李志军等[9]采用PLC(Programmable Logic Controller)、模拟量输入、输出模块搭建了一套装置,并通过OPC(Object linking and embedding for Process Control)技术将PLC与仿真平台连接,从而实现对水箱液位的控制。何迪[10]提出了一种带有模糊解耦的神经网络预测控制策略,对不同的期望液位,均能达到较好的跟踪效果,且不需要改变系统内部参数,鲁棒性较强。然而这些研究仅限于仿真分析,并没有进行实物验证。赵一博[11]利用OPC通讯技术将Matlab与PLC/HMI(Human Machine Interface)工业控制系统进行集成,开发出一套基于Matlab/Simulink实时网络控制的四容水箱实验系统,并分别验证了多变量内模PID(Proportion Integral Differential)控制算法和模型预测控制算法的有效性。研制出一套具有开放算法、操作简便、稳定可靠、人机交互界面友好等特点的四容水箱实验装置,对科研和教学均有很大助益。

笔者研究了一套自主设计开发的四容水箱实验装置,设计了分散内模控制器进行液位控制,该控制器具有结构相对简单、可调参数少、易于实现的优点。实验结果表明,该实验装置应用于自动化专业实验教学中,具有较好的教学和实验效果。

1 四容水箱实验装置设计

四容水箱实验装置设计分为硬件和软件2部分。图1给出了搭建的四容水箱实验装置的实物图,图2给出了四容水箱系统的物理模型示意图。该装置的2个水泵分别为水箱1～4供水,其中水泵1为水箱1、4供水,水泵2为水箱2、3供水。水箱1～4底部均设有1个排水阀,水箱3排出的水流入水箱1中,水箱4排出的水流入水箱2中。水箱1、2流出的水进入储水箱。管道内设有多个阀,通过调整阀门开启角度的大小,可实现对各水箱进、出水量的控制,能对水箱的性能进行相应的调整。

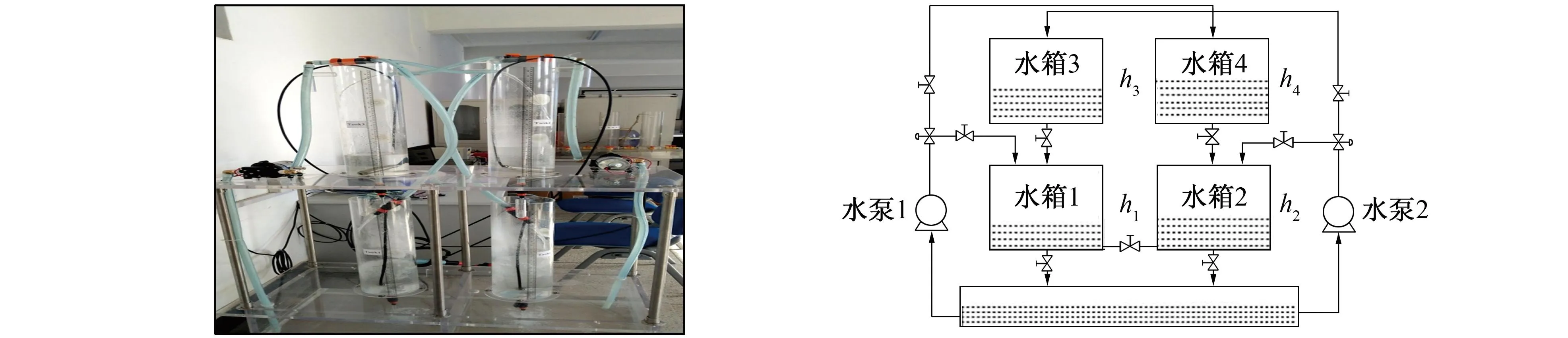
图1 四容水箱实验装置实物图

1.1 实验装置硬件设计

选取工业上常用的硬件设备,主要包括工控机、PCI(Peripheral Component Interconnection)数据采集卡、控制泵、差压传感器等。硬件主要选型及参数如表1所示。

表1 四容水箱实验装置硬件参数

图3为四容水箱系统控制流程图。该系统在工作过程中,由液位变送器对4个水箱的水位进行探测,并将其液位值输出为模拟电压。数据采集卡进行模数转换,然后通过Matlab编制的控制算法利用计算机对整个系统进行控制。控制器输出的控制量经过数据采集卡完成数模转换,通过控制直流电机调速器间接控制水泵的电压,进而实现水泵流量的精确控制。结合不同阀门开启关闭的配合情况,实现不同水箱水位的精确控制。

图3 四容水箱系统控制流程

1.2 实验装置软件设计

软件系统主要通过Matlab编程实现。学生利用Matlab/GUI操作界面完成四容水箱系统液位的设置,并实现数据采集和图形显示等不同的功能。

为使该实验装置可以提供一个开放性的算法验证平台,选择采用模块化的方法完成四容水箱系统的软件设计。主要由参数设定、人机交互、控制功能、图形显示、算法选取和数据采集6个模块组成,其总体结构如图4所示。每个模块的详细功能如下。

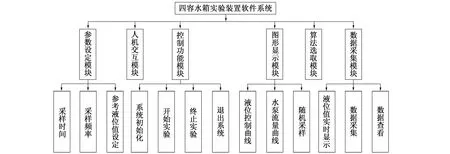
图4 四容水箱系统软件系统结构图

1) 参数设定模块。操作人员可在参数设定模块中,设定基准液位的数值、采样时间和频率。

2) 人机交互模块。其是操作人员与四容式水箱系统进行互动的窗口,其上设有其他5个功能模块的按键,只需对相应按键进行操作即可实现相应的功能。该实验装置具有良好的人机交互画面,能提高学生的学习兴趣,具有良好的教学效果。

3) 控制功能模块。该功能模块实现了系统的初始化、启动、停止、退出等操作。

4) 图形显示模块。在人机交互界面中,利用坐标轴的数据曲线显示,能很容易地观测各个水箱中的水位变化情况及水泵1、水泵2的流量情况,并具有数值显示功能。

5) 算法选取模块。四容水箱系统可以实现多种控制算法,操作者将不同的算法模块输入Matlab的算法程序中,即可完成对四容水箱系统水位值的调整(用户可在Matlab中直接编程,更改控制算法)。

6) 数据采集模块。实现对液位变送器模拟信号的采集,以及对控制信号的输出,通过人机交互画面,完成数据存储和查看等功能,为后续数据展开分析和处理提供了便利。

为使四容水箱系统操作更简捷、友好,利用Matlab/GUI设计了四容水箱系统的操作界面。如图5所示,该操作界面主要包括控制、数据采集、图形显示和参数设定4个区域。各区域的详细功能如下。

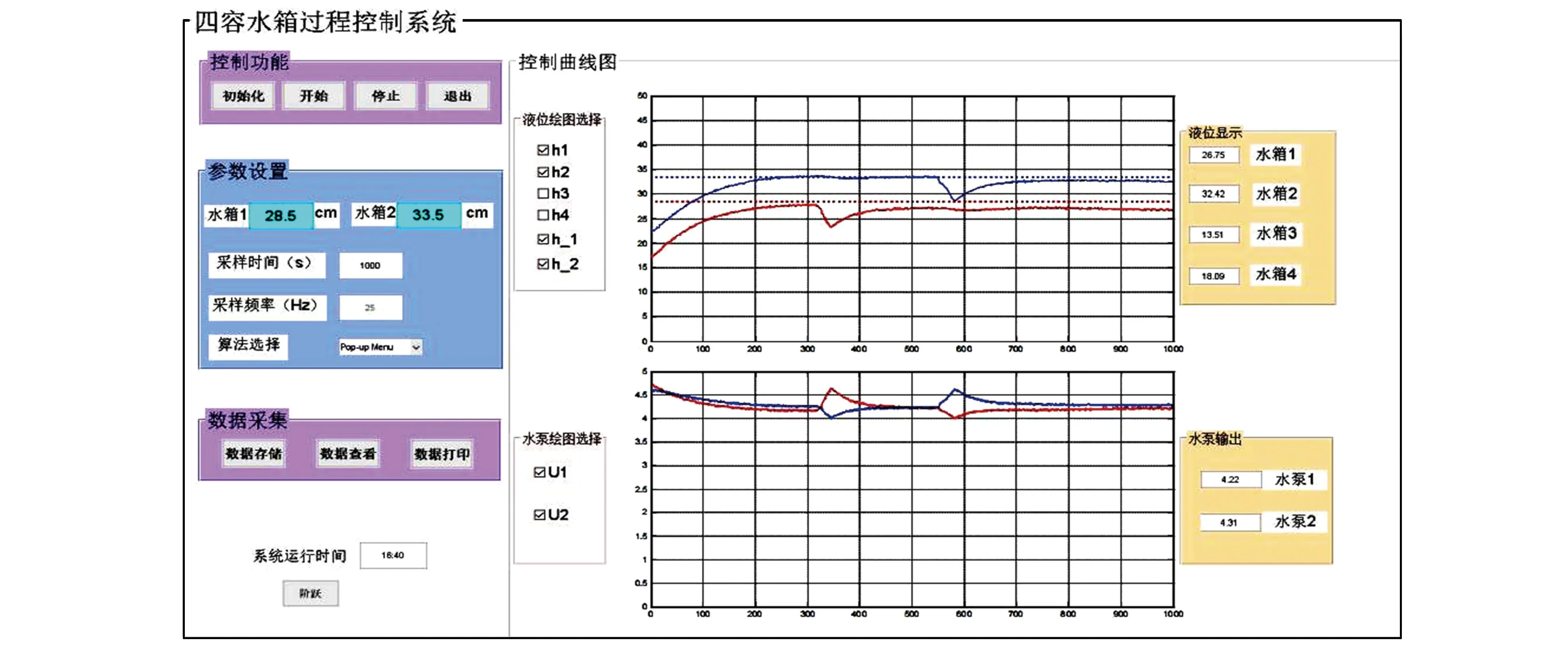
图5 四容水箱系统操作界面

1) 控制功能区域。该区域以启动、停止、退出为主要功能,完成对系统流程的控制。使用初始化功能,可将系统设定的参数写进注册表,并将实验装置的参数输入Matlab中。当按下停止键时,系统就会停止运行; 当按下退出键时,离开本系统,同时清除本系统所设定的采样参数,但其数据会被自动保存。

2) 数据采集功能区域。该区域具有数据的存储、查看和打印功能。数据以*.mat和*.xls等格式保存在Matlab中,通过Matlab操作界面打开文件夹即可实现数据查看功能。

3) 图形显示区域。在该区域,学生通过观测系统状态的实时曲线,可以了解整个系统的控制流程,从而进一步加深对理论知识的理解。图形中有两个坐标轴以及复选框,通过对复选框的操作,可以实现水泵1、水泵2流量变化曲线和水箱1～4水位高度变化曲线的显示。

4) 参数设定区域。该区域可针对数据采集卡的选型,设定不同的采样时间、采样频率和液位基准值,控制算法在下拉菜单中进行选取。

2 四容水箱系统数学模型与参数辨识

2.1 四容水箱系统数学模型

根据动态物料平衡关系以及伯努力方程可得到四容水箱系统的非线性方程组[12]:

(1)

其中hi和Ai分别为i号水箱的液位高度和截面积,ai为i号水箱底部出水孔截面积,g为重力加速度,且满足Qj=kjvj,Qj、vj、kj分别为j号水泵的流量、控制电压和比例系数,γj∈[0,1]。本文中,i=1,2,3,4,j=1,2。四容水箱系统参数如表2所示。

(2)

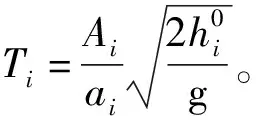
(3)

其中cj=Tjkj/Aj。

2.2 四容水箱系统参数辨识

实验装置通过阶跃响应参数辨识法[13]对四容水箱系统传递函数的参数进行辨识,首先要确定辨识模型结构,然后借助Matlab工具箱完成参数辨识。

以水泵1、水泵2的电压控制量v1、v2作为输入量,水箱1、水箱2的液位高度h1、h2作为输出量y1、y2,则其对应的传递函数矩阵可写成:

(4)

根据四容水箱系统的机理模型式(3),G11,G22近似为一阶惯性滞后环节,因此选择辨识模型结构如下:

(5)

G21,G12近似为二阶环节,其模型结构如下:

(6)

通过辨识得到系统的传递函数如下:

(7)

辨识得到传递函数G11、G12、G22的时滞项Td=0,传递函数G21的时滞项Td=0.15,由于时滞很小,设计控制器时可忽略不计,系统的传递函数如下:

(8)

3 四容水箱系统分散内模控制

分散内模控制又称为分布式内模控制或主回路内模控制[14-15],将耦合回路视作对主回路的干扰,针对主回路,笔者提出一种基于单变量的内模控制器方案,该控制方案不需要对原系统进行解耦。

四容水箱系统为双输入双输出耦合系统,以分散内模控制的设计思想为基础,将水箱1水位受水泵1的影响,水箱2的水位受水泵2的影响作为主回路,将水箱2的水位受水泵1的影响,水箱1的水位受水泵2的影响视作干扰,以此设计控制器。控制结构如图6所示。图6中r1(s)、r2(s)为参考输入,CIMC1(s)、CIMC2(s)为内模控制器,G11(s)、G22(s)为过程模型,P11(s)、P21(s)、P12(s)、P22(s)为被控制对象,y1(s)、y2(s)为输出。

图6 四容水箱系统分散内模控制结构

假定过程模型与实际被控对象匹配,即Pjj(s)=Gjj(s)。设计内模控制器CIMCj(s)分为两步。

第1步:模型分解。将过程模型Gjj(s)分解成2部分:

Gjj(s)=Gjj+(s)Gjj-(s),

(9)

其中Gjj+(s)为过程模型Gjj(s)中的不可逆部分,Gjj-(s)为过程模型Gjj(s)中可逆部分。由式(8)可知四容系统过程模型中不含有时滞、惯性环节及右半平面零点,即Gjj+(s)=1,所以

(10)

(11)

第2步:设计CIMCj。内模控制器结构如下:

(12)

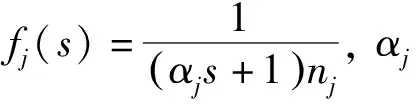
滤波器阶数的选择应保证CIMCj(s)正则有理。在设计内模控制器时,滤波器中的参数αj是唯一可整定的参数,该方法不仅能有效地消除系统中的随机扰动,而且能有效地解决模型失配的问题。引入滤波器fj(s)使控制器具有较好的控制质量和较强的鲁棒性。因此,根据式(12)设计内模控制器如下:

(13)

(14)

为保证内模控制器正则有理,这里取滤波器的阶数n1=n2=1,则式(13),式(14)可改写如下:

(15)

(16)

其中α1和α2的大小可调,其取值越小,系统的响应时间越短,相反系统的稳定性和鲁棒性越好。

4 四容水箱系统分散内模控制仿真与实验

为检验所设计的实验装置的合理性以及分散内模控制器的有效性,笔者分别进行了Matlab仿真与实物实验。

分散内模控制的仿真结果如图7所示。最初的水位设置值为水箱1的26 cm和水箱2的32.5 cm。在时间为910 s时,水箱1的水位值跳变到30 cm; 在时间为1 380 s时,液面水位值跳变到26 cm。在时间为700 s时,水箱2的水位值跳变到37.5 cm; 在时间为1 200 s时,液面水位值跳变到32.5 cm。如图7所示,分散式内模控制可以迅速追踪四容水箱系统设置的水位值,而不会出现超调。同时,该系统还可以对所设置的水位值进行快速跟踪,且一个水箱不同的液面水位设置值,对另一个水箱的影响很小,因此,该系统具有良好的抗干扰性。

图7 四容水箱系统液位高度(仿真)

分散内模控制的实验结果如图8所示,与仿真情况类似,水箱1和水箱2的液位设定值与仿真相同。从图8可知,四容水箱系统采用分散内模控制时,在170 s内能跳变到所设置的水位值,并且两个水箱之间的液位变化对彼此影响很小,系统具有较好的控制结果。

5 结 语

笔者自主研发设计的四容水箱实验装置具有操作简单、算法开放、性能稳定的特点。控制算法可直接在Matlab中编程,简化了对系统的操作。根据四容水箱系统辨识模型设计了分散内模控制器,在实验装置上进行液位控制实验。仿真和实验结果表明,内模控制器具有良好的动态性能和抗干扰能力,同时也验证了该四容水箱实验装置设计合理,达到了预期的设计目标。实验结果表明,该实验装置具有操作简单、稳定可靠的优点,在实验教学的应用中,取得了如下教学效果:1) 熟练掌握Matlab的使用方法和利用其进行系统仿真和设计; 2) 掌握四容水箱数学建模方法及控制器的设计步骤,为学生日后设计类似控制系统打下基础; 3) 熟悉工控机、采集卡、传感器等常用的实验硬件,掌握实验技巧和流程。

学生对在计算机上完成的实验没有直观感受,而对亲自动手的实验会倾入极高的热情和积极性,四容水箱实验装置的研发能不断促进学生在实践中发挥主观能动性,进一步提高教学质量和教学效果。这种实验形式既能提高学生的科研兴趣,又能提升学生的动手操作能力,同时还能培养学生的团队合作精神。