基于云模型的航材保障效能评估研究

李丽，闫树森，孙伟奇

（海军航空大学青岛校区，青岛 266041）

引言

航材保障作为航空装备保障的重要组成部分，直接影响着海军的战斗力，其质量的优劣直接影响着飞机战训的完好性、持续性和效益性，也关乎着海军装备保障能力形成的快慢、保障效率的高低、综合战斗力的生成。

1 航材保障效能评估含义

评估是根据一个给定的标准或尺度对事物进行科学严谨的分析度量，并且给出具体研判结果的过程。

所谓效能评估，就是先确定评价对象的各项影响指标，根据已知条件，引入适当的方法，建立其评价体系，得出评价结果并进行分析。效能评估的目的是得出各项指标的具体参数，分析并找出影响保障效能的原因。对于海军航空兵部队来说，航材保障效能评估是一个具有指导意义的工作，究其本质，属于多指标决策问题的一种。本文是针对海军航空兵基层航材单位的航材保障效能所进行的评估。评估的目的是对航材单位所开展保障工作的质量进行科学地评估，以此反映出其工作质量，帮助场站航材保障部门查找自身原因，弥补不足，提高海军航空兵基层航材单位的综合保障能力。

2 航材保障效能评估指标选取

基于实战要求，我军基层航材股的保障工作要做到稳定可靠，就是要平稳有序推进各项工作，保证在执行任务、演习演练、应急保障过程中保障有力，从而有效地促进生成战斗力。航材保障是一项复杂的系统工程，需要在注重军事效益的同时兼顾经济效益，对于航材保障工作的评估需要综合各方面因素才可以客观实现。航材保障效能评价指标的选取主要基于日常开展航材保障的相关活动，对于飞行任务的完成有着不可替代的作用。此外，评价指标作为基础的评价依据，对于整体研究具有决定性意义，需要进行科学考量[1]，因此将航材保障效能评价指标分为三大类：军事性指标、经济性指标和服务性指标，具体评价指标分级如表1 所示。

3 云模型原理

云模型是在我国提出并发展至今的。1995 年，隶属云思想由我国工程院院士李德毅率先提出，为研究处理模糊集合理论中隶属函数的不足之处所带来的影响，提供了一种具有数字特征云模型的解决思路，为后续的研究发展奠定了基础；1998 年李德毅院士又和学者杨朝晖发表了关于二维云的定义以及二维云模型的发生算法的学术文章[2-4]；徐兆文等将云模型理论应用到部队战时通信装备保障评估工作中，研究分析某单位遂行训练任务时的通信装备保障效能。在计算得到各评价指标权重后，利用云数字特征的不确定性的特点，将权重通过云测评发生器计算得出评估结果，实现了评价通信装备保障效能过程中定性语言与定量数据的互相转化，并依据评估结果对通信装备保障能力做出综合判断[5]。

2017 年LIU 提出了云距离集结算子、云加权平均距离算子、云权重几何平均距离算子以及云广义加权平均距离算子等概念，并完成了将自然语言值转化到云模型这一重要突破[6]。至今为止，云模型相关理论已经发展的较为全面，也逐渐地运用于各种领域[7-9]。

3.1 云模型定义

云模型，和看到的在天上飘浮的云一样，有着相似的不确定性，可以进行变换。这个概率密度函数与古典概率密度函数大相径庭，其表现为一对多的数学映射的散点图，其中没有固定的界限，没有固定的值，同时还能够随着时间的推移发生变化。具体定义如下：

设C 是一个概念（语言），如果x（指标）∈U 是概念C 在论域U 上的一次随机实现，则x 对C 的确定度μ（x）∈[0，1]是有稳定倾向的随机数：

则x 在论域U 上的分布称为云，x 称为云滴。

云滴是一种定量的表达方式，它可以用来描述云的数字特征，它的形成可以揭示出定性概念与定量值之间的复杂关联，从而实现云的生成。

Ex、En 和He 三个指标描述了云的数学特征。Ex 是在云图中表示云的重心位置，也是模糊概念的中心值，Ex 是最能够代表定性概念的；En 是概念不确定性的度量，它的数值大小反映了在论域中可被模糊概念接受的云滴分布范围；He 反映了云滴的凝聚程度，数值越大，则生成的云图中云滴的离散程度越大，隶属度的随机性也随之增大，云的厚度也越大。通常He 的数值比较小，取值小于0.1。因此，在云模型中，随机性和模糊性的关联程度可描述为：在云滴图中，靠近期望值Ex 的范围内云滴出现的概率大，表示某个定性概念的确定度比较大；远离期望值范围内云滴出现的概率小，表示某个定性概念的确定度比较小[10]。

3.2 逆向云发生器

云发生器是人为设计的用来实现云模型的算法，常用的共有四种发生器，这里介绍逆向云发生器[11]。

逆向云发生器可以将云滴的数据进行有效的分析，将给定的云滴的3 个特征数字转化为可以用于定性分析的结果，以便更好地识别云滴的变化趋势，并且可以更准确地预测云滴的变化情况，如图1 所示。

图1 逆向云发生器

算法如下：

1）根据xi计算这组数据的样本均值：

2）一阶样本绝对中心距：

3）样本方差：

在这个发生器中，输入的是n 个样本点的估计值（具体数字），输出的是用来描述定性概念的（Ex，En，He）云数字特征。

3.3 各指标云评价集

在应用云模型进行综合评估时，需要指标集Q、评语集P、权重集W。现对评语集P 进行界定与说明。

通过研究相关资料，并咨询部分专家意见后，确定采用9 级评语（非常差、极差、很差，差，较差，一般，较好，好，很好）构成本文评语集P，评价结果的顺序是按照对应的数值大小排列的，都在0-1 这个区间里，依次为（0.1，0.2，0.3，0.4，0.5，0.6，0.7，0.8，0.9）。即确定9 个评语值区间[pmin，i，pmax，i]，i=1，2，…，9。其中pmax，i，pmin，i分别表示第i 个区间的边界值（即最大值和最小值）。然后可得9 个评估指标云模型的数字特征：

Pi（Ex，i，En，i，He，i）。进而利用MATLAB 生成参考标准图。

评语集具体实现步骤及公式：

1）求出第i 个区间的期望值 Ex，i=（pmax，i+pmin，i）/2，（4-1） 其 中： 当 pmin，i=0 时， Ex，i=0，pmax，i=1，Ex，i=1。

2）求出第i 个区间的熵En，i=（pmax，i-pmin，i）/6，其中：当 pmin，i=0 或 pmax，i=1，En，i=（pmax，i-pmin，i）/3。

3）确定He，i=k，k 值为常数。超熵的大小反映了评价值的随机性，取值越大，随机性越大，产生的误差也就越大，对评估结果产生一定的影响。

依据公式，求得各评语集标准云数字特征：

P1（0.1，0.017，0.01），对应评语为非常差；P2（0.2，0.017，0.01），对应评语为极差；

P3（0.3，0.017，0.01），对应评语为很差；P4（0.4，0.017，0.01），对应评语为差；

P5（0.5，0.017，0.01），对应评语为较差；P6（0.6，0.017，0.01），对应评语为一般；

P7（0.7，0.017，0.01），对应评语为较好；P8（0..8，0.017，0.01），对应评语为好；

P9（0.9，0.017，0.01）。对应评语为很好。

对应的标准评价云图如图2 所示。

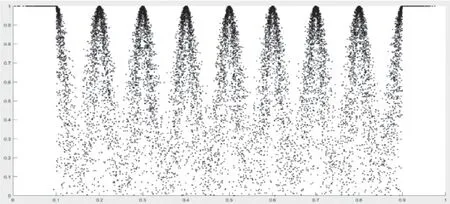
图2 标准评语集云图

3.4 云重心评判法

云重心可以表示为O=a×b，a 表示云重心的位置，即a={Ex1，Ex2，…，Exn}；b 表示云重心的高度，b={ω1，ω2，…，ω1}。Ex 表示相对应指标的模糊概念的信息中心值和云重心位置，当Ex 发生变化时，其表示的信息中心值会发生变化，云重心的位置也会随之改变。Ex 数值相同的云，比较其大小时可以比较云重心高度b的数值大小，b 的数值越大，其重要程度就越高，因此云重心高度b 在一定程度上反映了云的重要程度。而从整体角度出发，通过云的重心的变化情况可以体现出系统状态信息的变化情况。

4 实例分析

本文以海军某战区多个基层航材单位为评估对象，研究现阶段基层航材保障单位的保障效能，找出基层单位航材保障能力的短板，以提高基层航材单位的保障效能。

4.1 层次分析法计算权重

在航材保障效能评估的实施过程中，通常会有一部分难以量化的指标，和不可以直接进行互相比较赋值的指标，处理这些指标时，需要评价者根据自身主观经验进行判断并进行赋值，因此采用主观赋值法确定航材保障效能评估指标体系的权重。针对主观赋值法，使用层次分析法来计算各级评价指标的权重。

采用1-9 比较尺度构造成对比较矩阵，进行归一化处理，进行一致性检验，计算出指标权重。

一级指标权重值见表2。

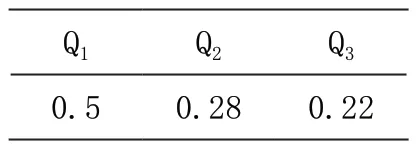
表2 一级指标权重

二级指标权重值见表3 所示。

表3 二级指标权重

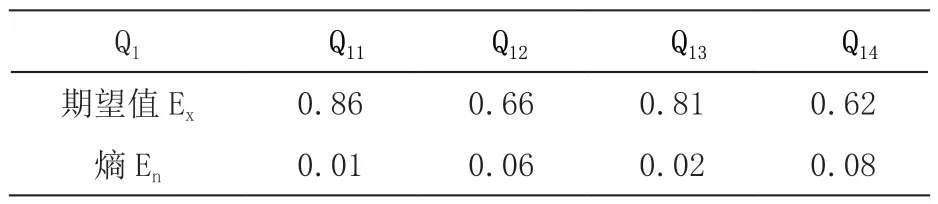
表4 军事性二级指标的云数字特征

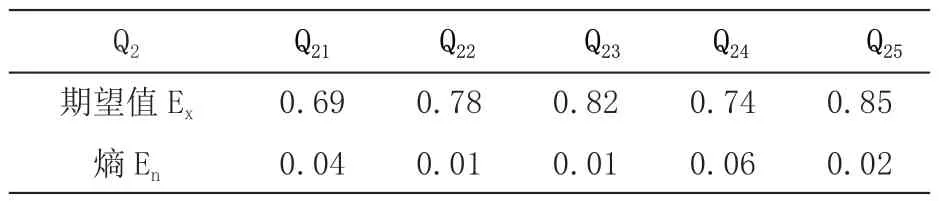
表5 经济性二级指标的云数字特征

表6 服务性二级指标的云数字特征

4.2 引入云模型

4.2.1 求解各指标云数字特征

应用MATLAB 软件，将权重值带入逆向云发生器中，输出结果即二级指标的云数字特征。

4.2.2 应用云重心评判法

求得：

得到一级指标的偏离度为：

则一级指标对应的评估值为：

由表2 可得：

ω1的数值大小为0.5，ω2的数值大小为0.28，ω3的数值大小为0.22，因此可得综合评估值：p=p1*ω1+p2*ω2+p3*ω3=0.72。

由上可得：军事性指标评估结果为0.68，处于“一般”区间；经济性指标评估结果为0.74，处于“较好”的区间；服务性指标结果为0.80，处于“好”的区间；该航材保障单位综合评估结果为0.72，处于“较好”区间。

5 结束语

以基层航材保障单位为依据，分析影响基层航材保障单位保障效能的因素，构建航材保障效能评估指标体系，邀请部队专家打分得到基础数据，运用云发生器得到各指标云数字特征，运用云重心评判法得出指标的加权偏离度，并激活对应的评价语言；总加权偏离度的数值为0.72，激活的评价语言为较好。通过引入云模型，解决评估过程中模糊性和随机性即不确定性所带来的问题，设计算法进行效能评估，结果显示，总的保障效能和每个一级指标的效能都能够直观地表示出来，将评估结果与等级标准作对比，能够清晰地看出目前各项工作的好坏，为航材保障工作提供一定的借鉴指导。