多层印制电路板镀通孔应力-应变MBPTH 模型

牟浩文，高俊超，魏宸鹏，宁薇薇

（天津航天瑞莱科技有限公司，天津 300462）

引言

镀通孔作为印制电路板的关键组件，其可靠性也就成为了印制板可靠性问题的关键因素。PTH 主要的失效机理是热循环疲劳，失效原因是PTH 的金属镀层材料与印制电路板的基板材料热膨胀系数不匹配。

镀通孔可靠性评估对于镀通孔设计、提高可靠性有很重要的作用。国内外专家学者从解析、有限元法分析和实验三个角度对其失效物理模型的建立和影响因素做了大量研究。Oien[1]和Nankey[2]提出了一个一维模型来估计PTH 的应力/应变响应，预测一个热循环后残余应变分量。IPC[3]模型将镀通孔结构中的镀层和印刷电路板分别简化为分离的一维杆结构，给出了弹塑性范围的应力应变表达式，但此模型不满足PTH 镀层端面的临界自由条件，以及镀层基板粘结处的位移连续条件，谢劲松[4]等通过考虑铜-树脂表面剪切应力对此模型进行了改进，分析了镀通孔轴向方向的应力-应变分布情况。Mirman[5]将焊盘结构简化为梁结构，考察了在热循环载荷作用下不同参数对PTH 可靠性的影响。马里兰CALCE[6]中心在假定轴向应变和每个板层厚度方向应力相同的条件下，通过类比机械系统线性弹簧模型建立了应力-应变模型。R.Iannuzzelli[7]利用有限元模型考察了PTH 焊盘与镀层结合处的应变分布。

目前镀通孔应力-应变模型研究中还存在一定局限性，大部分模型把镀通孔简化为一维结构，没有考虑多层板结构和外部焊盘因素。本文在对多层印制板镀通孔结构做合理简化的基础上，结合弹性薄板内径简支和外径自由的基本力学方程以及边界条件，推导出多层印制板镀通孔的应力-应变模型，并利用有限元分析验证了不同温度条件和不同几何参数组合下解析模型计算的合理性和准确性。

1 多层板镀通孔应力-应变模型研究

1.1 镀通孔结构的简化

镀通孔从结构上来说，主要包括镀层孔壁和外部焊盘。但多层电路板中的镀通孔内表面和无功能焊盘对其应力-应变也存在一定程度的影响。根据文献[8]结果可知内表面和无功能焊盘对镀通孔的影响可以合并，为了求解方便将镀通孔简化为如图1 所示的结构。

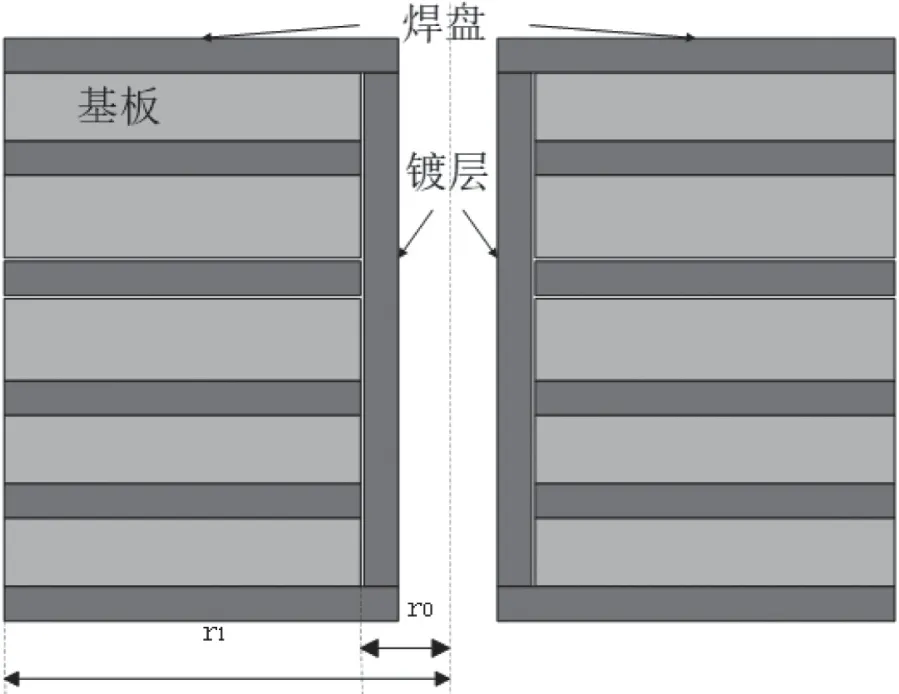
图1 镀通孔简化结构示意图

基于图1 结构，初步建立假设条件如下：

1）PTH 为轴对称结构；

2）各基板层厚度相等，板层材料为FR-4 环氧玻纤布（这种材料以环氧树脂作为粘合剂，以玻纤布为增强材料而构成绝缘层），镀层和焊盘材料为铜，且厚度相等，焊盘半径都相等；

3）在加载中，镀铜和板层材料都没有发生蠕变；

4）PTH 结构中的温度分布是均匀的。

基于这种简化结构建立的应力-应变模型是适用于解决多层板中的镀通孔应力-应变分析，所以后文都将这种模型简称为MBPTH（Multilayer Board’s Plated Through Hole）。

1.2 MBPTH 模型的建立

应力分布模型的建立是在Mirman 模型梁结构的基础上开展的，模型建立过程中包含的假设条件为：

1）把焊盘结构看做环形圆板并受到均布载荷qj，内边缘简支，外边缘自由；

2）镀层材料遵循应力/应变图，如图2 所示；

图2 镀层材料的线弹性和线塑性应力-应变关系

3）焊盘、树脂材料是线弹性；

4）PTH 结构的温度是一致的；

5）假设影响PTH 变形的PCB 部分是一个空心圆柱，内径等于孔径，外径等于焊盘直径。

基于假设和简化结构常微分方程如式（1）：

式（2）为线性非齐次常微分方程，其通解可以表示为方程某一特解w*与相对应的齐次微分方程（3）的通解之和的形式：

解常微分方程可得：

利用有限元分析验证了多层电路板的等效应力分布近似均匀，分析结果如图3 所示。图3（a）显示当外部焊盘：内部焊盘：板层宽度=1 ∶1 ∶ 1 时外部焊盘、内部焊盘和镀层的等效应力分布情况，颜色的深浅表示应力的大小，从图可以看成应力在每一层近似均匀。图3（b）显示当内部焊盘：外部焊盘：板层宽度=1 ∶2 ∶2 时外部焊盘、内部焊盘和镀层的等效应力分布情况，颜色的深浅表示应力的大小，从图可以看出应力在每一层近似均匀。

1.3 最大应力-应变解析结果

通过有限元分析发现外部焊盘与镀层结合处应力最大，这与文献[9]有限元分析结果也是一致的，故分析外部焊盘r=r0处的受力情况。其中q1=0，w1（r0）=w2（r0）=0，

则弯矩方程为：

径向正应力σr和环向正应力σθ分别与Mr、Mθ成正比，表达式如（8）和（9）所示。

轴向正应力为：

其中式（9）和（10）中：

式（10）与Oien[1]提出的应力模型表达形式一致。

利用von Mises 等效应力作为失效判据，对镀通孔进行疲劳寿命计算。von Mises 等效应力为：

为了评估镀通孔寿命，需要建立应力和应变之间的关系。根据图2 所示的应力应变关系图，可知多层板镀通孔弹性和塑性范围内的应变解析表达式为：

2 多层板镀通孔有限元分析

2.1 镀通孔有限元模型描述

建立多层板镀通孔有限元模型，假设条件如下：

1）多层PCB 中间平面厚度是对称构成的；

2）各板层厚度相等，板层材料为FR-4 环氧玻纤布，镀层和焊盘材料为铜，且厚度相等，焊盘半径相等；

3）所有材料的粘合可承受预期剪切载荷，不考虑夹层分层或分离；

4）电路板的温度均匀分布；

5）FR-4 为均匀的，正交各向异性和线弹性。

有限元分析材料属性常数如表 1 所示[10-14]。

根据有限元分析假设条件建立的有限元分析结构如图4，图4（a）所示镀通孔共有六层基板层，五个内部焊盘层，两个外部焊盘层和一层镀层，图4（b）所示镀通孔共有八个基板层，七个内部焊盘层，两个外部焊盘层和一层镀层。

通过查阅IPC 标准[1]，获得不同几何参数在工程中的取值范围为：0.75 mm ≤H（板厚）≤2.5 mm，0.24 mm ≤r1（焊盘半径）≤0.8 mm，0.12 mm ≤r0（孔半 径） ≤0.4 mm，0.015 mm ≤t（ 镀 层 厚 度）≤0.06 mm，在有限元分析软件中建立模型选取的几何尺寸如表 2 所示。

2.2 有限元模型的分析结果

2.2.1 不同温度条件

基于图4 所示的八层板有限元模型，参数设置如表3 所示，施加温差ΔT 范围为（25~35）℃，不同温度条件下的等效应力和等效应变结果如表 4 所示，其中30 ℃孔壁分析结果如图5 所示。

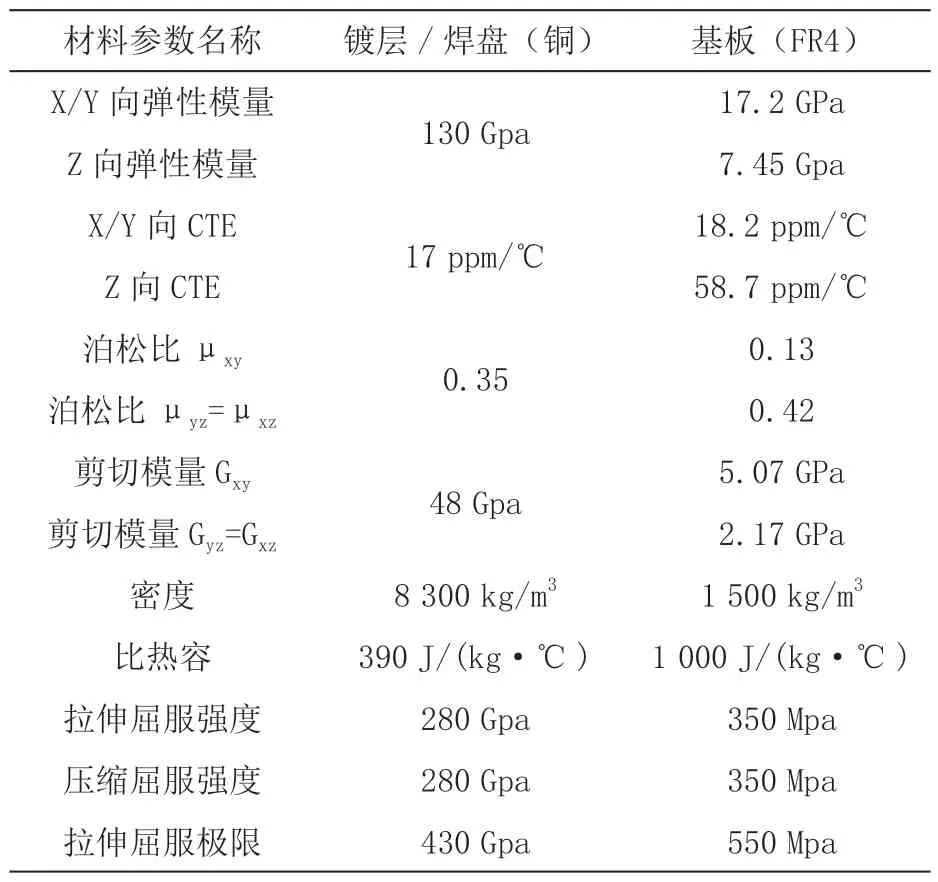
表1 材料属性常数

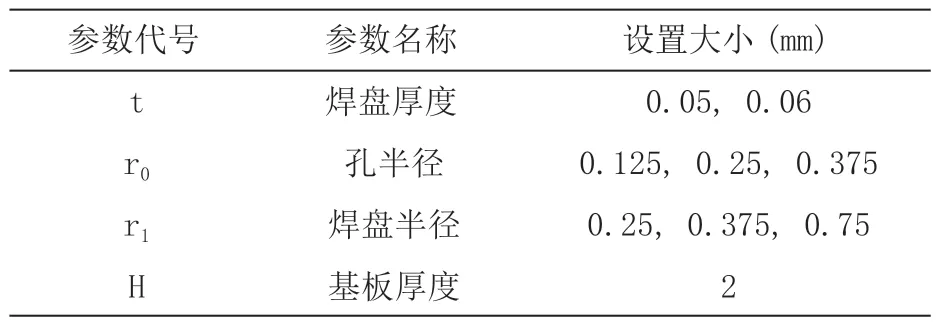
表2 有限模型参数设置情况

表3 有限元模型参数组合

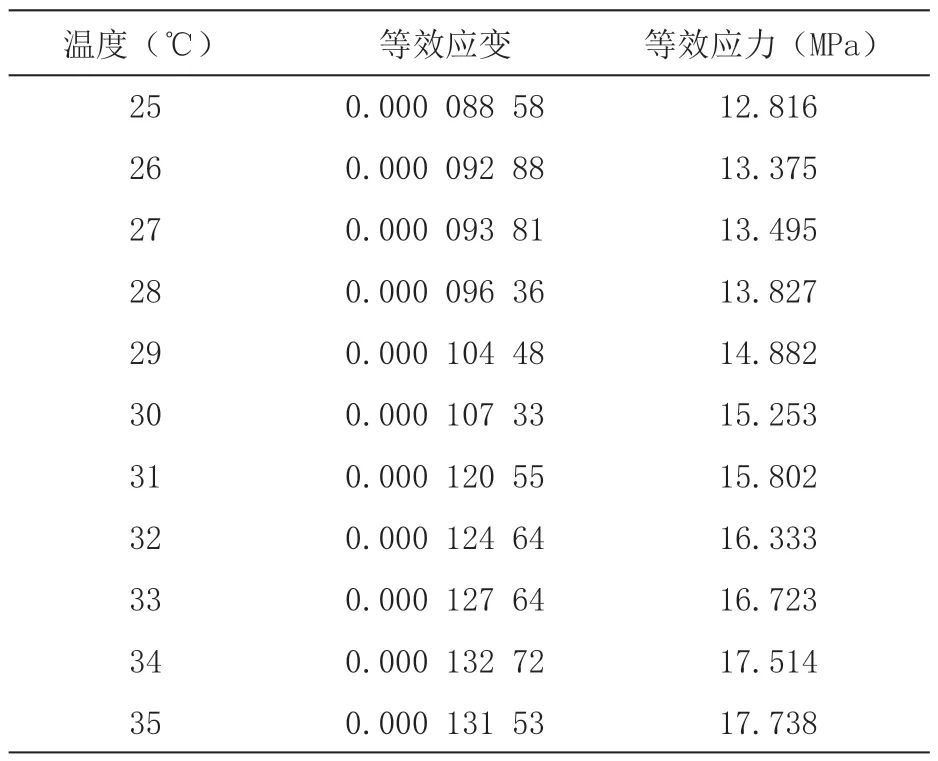
表4 有限元分析结果

表5 有限元分析结果

图5 30 ℃有限元分析结果

基于图4（a）和图4（b）所示的八层板和六层板基本有限元结构，建立不同孔径、焊盘直径和镀层厚度的有限元模型，然后施加相同的温度条件ΔT=30 ℃，获得等效应力和等效应变结果如表 5 和表 6 所示。编号为3和8 的有限元模型分析结果如图6 和图7 所示。

图6 样本3 有限元分析结果

图7 样本8 有限元分析结果

2.3 有限元分析结果与理论结果的比较

为了验证理论模型的准确性，利用2.2 节建立的MBPTH 模型计算不同温度条件和不同几何参数组合的理论结果。然后将有限元分析结果与理论结果作对比，计算误差大小。

2.3.1 不同温度条件

基于八层板表 3 所示的几何参数设置，利用MBPTH模型计算不同温度条件下镀通孔的轴向应力、径向应力和周向应力结果如表6 所示，理论结果和有限元分析结果对比情况如表7 所示。

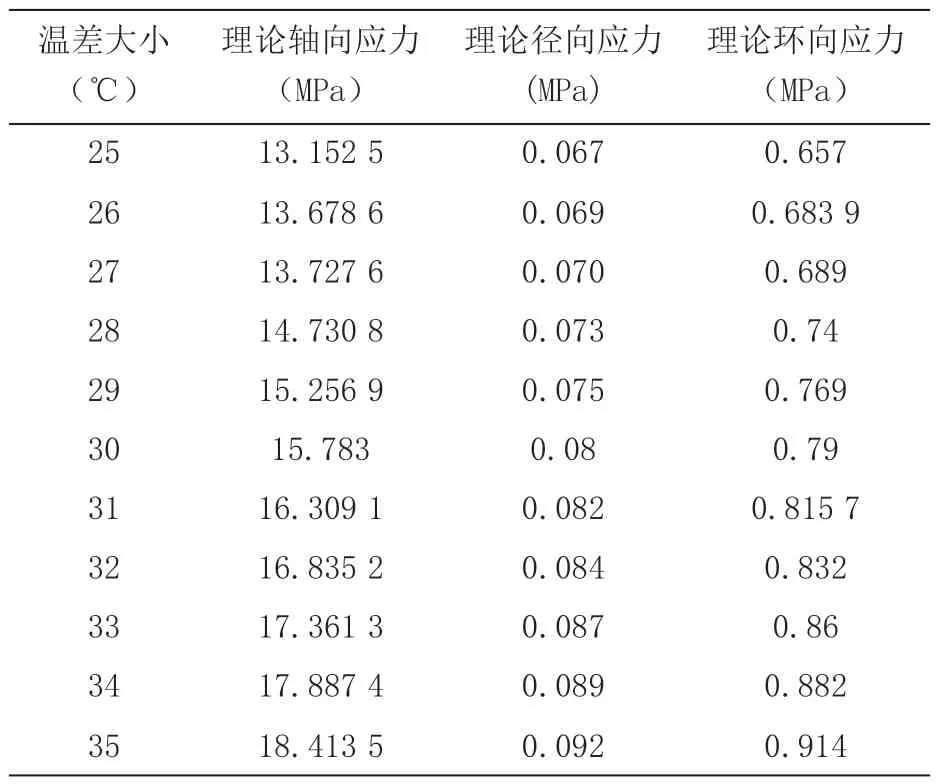
表6 模型理论计算结果

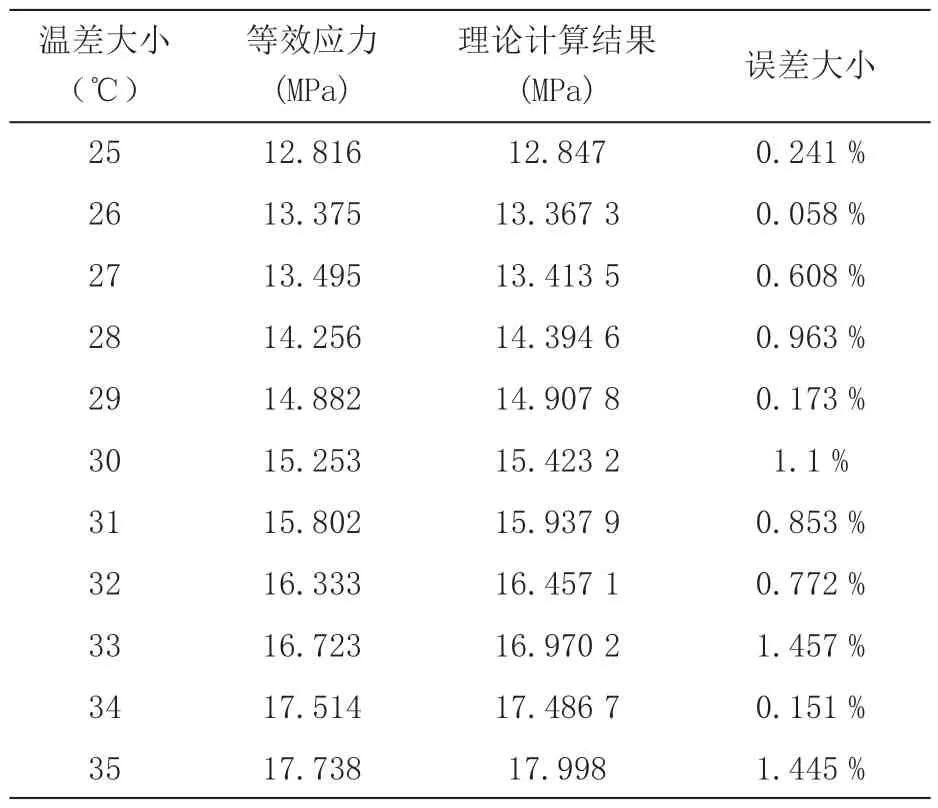
表7 理论结果和有限元分析结果对比情况

2.3.2 不同几何参数组合

利用MBPTH 模型计算上述10 个不同几何参数组合镀通孔ΔT=30 ℃条件下的理论结果，轴向应力、径向应力和周向应力结果如表8 所示，理论结果和有限元分析结果对比情况如表9 所示。

表8 不同参数组合的理论计算结果

表9 有限元分析结果与理论结果对比情况

通过表8 和表9 对比结果可以说明在一定的误差允许范围内，模型理论结果与有限元分析结果一致，验证了MBPTH 模型的准确性。

3 结论

本文在梁结构的基础上，利用圆形薄板内径简支和外径自由基本力学方程推导出多层板镀通孔不同位置的应力-应变情况结合边界条件给出了最大应力应变的解析结果。基于简化结构在有限元分析软件中进行了不同温度条件和不同几何参数组合下的应力应变分析，并与理论计算结果进行对比，验证了解析模型的合理性和准确性，为估算多层板镀通孔寿命提供了依据。