弹性延迟退休改革对子女人力资本投资和老年劳动供给的影响
李明桥,金瑀琦
(西南石油大学,四川 成都 610500)
一、问题的提出
未来20 年,我国将面临新增劳动力供给萎缩和人口年龄结构加速老化的双重困境。根据《2020年第七次全国人口普查主要数据》测算可知,2020 年我国0~60 岁各年龄段人口占比由高到低依次为41~60 岁、21~40 岁、0~20 岁。随着时间的流逝,0~20 岁年龄段人口不断变为新增劳动力,41~60 岁年龄段人口则逐渐退休,退出劳动力市场的人口规模大于新增劳动力规模,将导致老年抚养比不断上升从而加重社会养老负担。为应对人口老龄化对城镇职工基本养老保险基金可持续性的不利影响,党的二十大和2022 年底召开的中央经济工作会议均明确提出“实施渐进式延迟法定退休年龄”的政策目标。对于如何逐步延迟退休,从保险精算视角进行研究的文献争议的焦点在于是否应该“男女同步”以及最终的法定退休年龄是否应该存在性别差异等方面[1-4]。曾益[5]认为每年延迟6个月,直至男女法定退休年龄同岁(65 岁)是较为理想的选择,刘万[6]认为延迟法定退休年龄仍然应该存在性别差异,即男性65岁、女性60岁。这些文献的共识体现在延迟退休能提高养老保险基金的可持续性。
运用保险精算方法的前提条件是劳动者严格按照法定退休年龄退休,然而我国提前退休现象十分普遍[7],人力资源和社会保障部统计数据显示2015年我国企业职工平均退休年龄不足56岁。学界关于提前退休的研究成果也较为丰富[8-10],这些都表明保险精算方法的前提条件在我国不一定成立。当存在提前退休行为时,如果延迟法定退休年龄仅对政府部门和国有企业等单位的劳动者产生影响,而无法作用于中小微企业或灵活就业的劳动者,那么保险精算方法仍以法定退休年龄作为缴纳养老保险费的最大年龄就会高估养老保险基金收入,因此运用保险精算方法得出的研究结论有待商榷。
保险精算方法忽略了劳动者对延迟退休政策的反应,为弥补这方面不足,一些学者研究了延迟法定退休年龄政策下的劳动者应对行为。Vogel[11]使用世代交叠模型研究发现延长老年劳动供给时间有利于提高人力资本投资水平,增加的人力资本和延长的劳动供给时间共同作用,部分抵消了人口加速老龄化的不利影响。Fetter[12]研究发现政府对低收入老年人口的支持计划不仅没有延长劳动供给时间,反而促使老年劳动者积极退出劳动力市场。Simon[13]研究了法国把法定退休年龄由60 岁延长到61 岁的政策效果,发现该政策虽然延长了老年劳动供给时间,但是一些劳动者仍然在60 岁退出劳动力市场,通过失业补助金维持生活。上述研究表明在延迟退休改革中要关注劳动者对政策的反应,因此国内学者[14-16]建议在延迟法定退休年龄改革中引入弹性退休制度,也就是说政府在逐步延迟法定退休年龄的过程中,当劳动者的最优退休年龄大于法定退休年龄时,劳动者仍然有选择继续工作的权利。弹性退休制度把何时退休的权利赋予劳动者,可避免改革后的法定退休年龄还存在“一刀切”的问题。如果政府施行弹性延迟退休政策,那么劳动者就会根据个人情况选择合适的退休年龄,这样的制度安排既延迟了退休年龄又关注了劳动者福利,有利于减少延迟退休改革的阻力。
现有文献虽然关注了弹性延迟退休制度,但是鲜有文献研究该制度对养老保险基金的长期影响。为弥补这方面的不足,本文以弹性延迟法定退休年龄政策作为研究背景,运用世代交叠模型研究劳动者退休年龄的选择问题。研究目标在于分析弹性延迟退休政策下劳动者的决策行为,以及这种决策行为对养老保险基金可持续性的影响。具体研究思路如下:首先,劳动者选择退休年龄的目标是实现终身效用最大化,劳动者效用水平由消费、退休闲暇、子女人力资本三部分构成。其次,模型中劳动者生存时间可分为成年期和老年期两个阶段,在第一阶段劳动者不但需要花费物质成本抚养子女,而且为了培育下一代人力资本还需要花费时间教育子女,因此劳动者在成年期面临工作时间和教育子女时间的分配问题,从而可确定教育子女的时间投资。当劳动者刚步入老年期时则子女进入了成年期,老年期劳动者已经在成年期完成了养育子女的任务,老年期时间分配问题演变为多少用于继续工作与多少用于退休闲暇,从而可确定老年劳动供给时间并间接推算出劳动者的退休年龄。最后,在保证养老保险基金收支平衡的前提下,弹性延迟退休政策的目标是既要延长老年劳动供给时间,又要激励劳动者增加教育子女的时间投入。如此制定延迟退休制度的原因在于:一方面,延长老年劳动供给时间既能减少养老保险基金支出又能提高基金收入;另一方面,增加教育子女的投入时间有利于增加下一代人力资本,而增加的人力资本能提高劳动者子女的工资收入,这样就会提高未来养老保险基金收入,这两方面共同作用能确保养老保险基金长期可持续。
二、理论模型
本文采用Koichi[17]和汪伟[18]的两期世代交叠模型分析框架,研究背景假定为政府实施弹性延迟法定退休年龄政策,也就是说如果劳动者偏好的退休年龄大于法定退休年龄,那么劳动者仍然具有继续工作的权利。因此在弹性延迟退休政策背景下,世代交叠模型的劳动者最优决策就确定了老年劳动供给时间,模型基本框架构建过程如下。
(一)劳动者(效用最大化)
在t期成年劳动者的终身福利水平Ut由消费(Cy,t和Co,t+1)、退休闲暇1-lt+1、子女人力资本ht+1三部分构成,具体如式(1)所示。假设劳动者在成年期和老年期都有1单位时间禀赋并且确定性地存活至成年期期末,在老年期生存概率为π。劳动者根据效用最大化原则配置成年期消费Cy,t、老年期消费Co,t+1、退休闲暇1-lt+1、子女人力资本ht+1。退休闲暇1-lt+1由老年期1单位时间禀赋扣除老年期劳动供给时间lt+1所得。参数θ表示劳动者对退休闲暇的偏好程度,θ值越大表明退休闲暇给劳动者带来的效用越大,劳动者越偏好提前退休。参数β表示劳动者主观贴现因子,β值越小表明劳动者越偏好当期消费Cy,t。参数n和σ分别表示养育子女数量和父母对子女的利他程度也就是父母关爱子女程度。参数σ值越大表明父母关爱子女程度越高,在此条件下子女数量n越多或者子女人力资本存量ht+1越大,则父母效用水平就越高。就子女人力资本ht+1的形成而言,本文采用Becker[19]的人力资本生产函数生成,具体如式(2)所示。其中:d表示教育部门生产率参数,ht和et分别表示t期成年劳动者人力资本和教育子女的投入时间。
劳动者在成年期(t期)的预算约束方程如式(3)所示,因为本文中工资率w表示具有1单位人力资本的劳动者工作1单位时间所获得的工资收入,所以wht为有效工资率也就是人力资本为ht的劳动者工作1单位时间所获得的工资收入。表达式(1-et)(1-τ)wht表示劳动者在成年期缴纳养老保险后的工资收入,其由有效工资率wht、成年期劳动时间1-et、扣除养老保险缴费后的工资占工资收入的比例1-τ三者之积构成。本文假定参数q(养育每个子女的物质成本)是劳动者工资收入的固定比例,因此(1-et)(1-τ)whtqn表示养育子女的总花费。由此可知:式(3)等号右边是劳动者在成年期的可支配收入,是劳动者在成年期的工资总收入扣除养老保险缴费和养育子女的物质成本后的收入;式(3)等号左边表示劳动者在成年期的可支配收入用于当期消费Cy,t和当期储蓄St的部分。值得强调的是,t期成年劳动者人力资本为ht时对应的个体储蓄为St,所以t期的总储蓄为StNtht,其中Nt为t期的成年劳动者人数。劳动者在老年期(t+1期)的预算约束方程如式(4)所示,因为Rt、r、lt+1分别表示t期资本收益率、养老金替代率、劳动者在老年期的劳动供给时间,所以劳动者在老年期缴纳养老保险后的工资收入为(1-τ)whtlt+1、老年期获得的储蓄总收益为RtSt、养老金为rwht(1-et+lt+1)。因此式(4)表明劳动者在老年期的所有收入都用于老年期消费Co,t+1。
(二)厂商(利润最大化)
假定厂商在完全竞争市场下使用物质资本和有效劳动进行生产,生产行为可由规模报酬不变的柯布-道格拉斯生产函数表示,具体如式(5)所示。其中,A、K、L、α(0≤α≤1)依次表示生产技术水平、物质资本存量、有效劳动供给、资本产出弹性。t期的有效劳动供给Lt是指在计算劳动供给量时不但要包含成年与老年两类劳动者数量(Nt和Nt-1)以及劳动时间(1-et和lt),而且要包含劳动者人力资本存量(ht和ht-1)。在弹性延迟退休政策下,t期的有效劳动供给是由t期成年劳动者的有效劳动Ntht(1-et)和t-1 期成年劳动者在老年期(t期)的有效劳动πNt-1ht-1lt两部分构成,具体如(6)式所示。把有效劳动的人均产出yt和有效劳动的人均资本存量kt分别定义为yt=Yt/Lt和kt=Kt/Lt,则式(5)可表示为
参照汪伟[18]的处理方法,本文假定世代交叠模型中1单位时间禀赋的时间跨度为30年,物质资本在各期内完全折旧。根据上述假定,在完全竞争要素市场下,厂商利润最大化下的有效工资率和资本收益率分别如式(7)和式(8)所示。由此可知∂(wht)/∂(kt)>0、∂Rt/∂kt<0,这表明其他条件不变时有效劳动的人均资本存量kt越大则当期有效工资率wht越高、资本收益率Rt越低,反之亦然。
(三)政府(养老保险基金收支平衡)
在弹性延迟退休政策下,成年期劳动者缴纳的养老保险费τ(1-et)whtNt由养老保险缴费占工资的比例τ(下文简称“缴费比例”)、个体工资收入(1-et)wht、劳动者人数Nt三者之积构成。同理,老年期劳动者缴纳的养老保险费τwht-1ltπNt-1由缴费比例τ、老年期个体工资收入wht-1lt、t-1期成年劳动者在老年期(t期)的存活人数πNt-1三者之积构成。养老保险支付给退休人员的养老金r(1-et-1+lt)wht-1πNt-1由养老金替代率r、劳动者在成年期和老年期的工资收入(1-et-1+lt)wht-1、t-1期成年劳动者在老年期(t期)的存活人数πNt-1三者之积构成。
政府的目标是确保养老保险基金收支平衡,t期养老保险基金总收入与总支出的预算平衡表达式如式(9)所示。因为n为成年期劳动者养育的子女数量,所以t期成年劳动者人数Nt可以表示为t-1期成年劳动者养育的子女数量(Nt=nNt-1)。t期成年劳动者人力资本ht与t-1 期成年劳动者人力资本ht-1的关系是由人力资本生产函数式(2)决定的,因而t期成年劳动者的人力资本表达式为ht=det-1ht-1。综上所述,养老保险基金总收入与总支出的预算平衡方程式(9)可变为以劳动者个体为依据的预算平衡方程式(10)。
(四)资本市场出清
资本市场出清条件为t期的物质资本总投资等于t-1期总储蓄。物质资本在各期内完全折旧的条件下,因为只有成年期劳动者才会发生储蓄行为,所以资本市场总投资与总储蓄的出清条件为式(11)。用资本市场出清方程式(11)除以有效劳动供给量Lt即式(6)可得出有效劳动下的人均资本存量表达式,具体如式(12)所示。
三、模型求解
(一)劳动者最优决策行为
在成年期式(3)和老年期式(4)的预算约束条件下,劳动者的决策目标是实现终身福利水平最大化。在给定有效工资率wht和资本收益率Rt的情况下,通过拉格朗日函数并结合式(2)的人力资本生产函数,可解得劳动者最优决策的欧拉方程,具体如式(13)~(15)所示。
第一,欧拉方程式(13)表明如果要实现终身福利水平最大化,那么劳动者就要平滑两期的消费水平,其中表示成年期1 单位工资收入用于当期消费所产生的效用增量。如果劳动者把成年期1 单位工资收入用于储蓄,那么在老年期获得的总收益就为Rt。因为表示老年期1 单位工资收入用于消费所产生的以成年期衡量的效用增量,所以表示劳动者把成年期1单位工资收入用于老年期消费所产生的以成年期衡量的效用增量。因此,当欧拉方程式(13)成立时,劳动者不可能通过调整两期消费水平来提高终身福利水平,这表明劳动者平滑了两期消费水平。
第二,欧拉方程式(14)表明如果要实现终身福利水平最大化,那么劳动者不但要确定成年期消费水平Cy,t,而且要确定当期教育子女的投入时间et。由效用函数式(1)和人力资本生产函数式(2)可知教育子女投入时间的边际效用为σ/et。因为欧拉方程式(14)中的表示如果劳动者把成年期的1 单位时间禀赋全部用于工作,那么劳动者以老年期衡量的终身总收入就是由成年期工资收入Rt(1 -τ)(1 -qn)wht和老年期养老金rwht两部分构成,所以式(14)中的表示成年期减少1单位工资收入所能换取的成年期时间。由此可知,式(14)等号右边表达式的经济学含义就是劳动者将在成年期减少1单位工资收入而节约的工作时间用于教育子女所带来的效用增量,而式(14)等号左边表示将成年期1 单位工资收入用于当前消费所带来的效用增量,当式(14)成立时说明劳动者在成年期作出了最优决策,从而确定了教育子女的投入时间。
第三,欧拉方程式(15)表明如果要实现终身福利水平最大化,那么劳动者不但要确定老年期消费水平Co,t+1,而且要确定退休闲暇时间1-lt+1。由于式(15)中的()1 -τ+r wht表示如果把老年期1 单位时间禀赋全部用于工作,那么劳动者在老年期的总收入就由缴纳养老保险后的工资收入(1-τ)wht和养老金rwht两部分构成,值得一提的是老年期劳动者没有抚养子女的物质成本花费,因此工资收入表达式(1-τ)wht中不包括1-qn,式(15)中的表示老年期减少1 单位收入所获得的退休闲暇时间。通过效用函数式(1)可得出消费和退休闲暇的边际效用分别为和因而式(15)说明劳动者为了实现终身效用最大化,在老年期增加1 单位收入用于消费所带来的效用增量要等于减少1单位收入而增加的退休闲暇所带来的效用增量。
(二)动态一般均衡求解
由资本市场出清条件式(12),结合劳动者预算约束方程式(3)~(4)、厂商生产要素方程式(7)~(8),以及满足劳动者终身福利水平最大化的欧拉方程式(13)~(15),可推导出稳态下以有效劳动衡量的人均资本存量k*的表达式,具体如式(16)所示,该式中各变量的计算方法如式(17)~(22)所示。因为稳态下的人均资本存量k*可最终由模型中的各参数表示,所以在此基础上可依次求出稳态下的有效工资率wh*、资本收益率R*、劳动者在成年期的消费、老年期的消费、教育子女的投入时间e*、老年劳动供给时间l*。考虑到稳态下以有效劳动衡量的人均资本存量k*表达式(16)较为复杂,所以本文采用数值模拟方法分析弹性延迟退休制度对劳动者教育子女的投入时间和老年劳动供给时间的影响。为了解劳动者决策行为的变化情况,本文以当前未实施延迟退休政策的现实情况作为研究背景构建基准模型,分析从当前退休制度转变为弹性延迟退休制度如何影响劳动者的决策行为(限于篇幅基准模型的构建及求解过程未列示,结果留存备索)。
四、参数取值与数值模拟结果分析
(一)参数取值与数值模拟应注意的问题
1.参数取值。本文把世代交叠模型中成年期和老年期的时间跨度都设定为30 年,具体参数设置规则如下:第一,主观贴现因子β反映了劳动者在老年期获得的1单位效用贴现到成年期的程度,β值越小则老年期效用贴现到成年期就越少,表明相较于老年期效用而言劳动者更关注成年期效用,反之亦然。参照Yew[20]的做法将各年主观贴现因子赋值为0.98,本文在30年时间跨度条件下的主观贴现因子取值为β=0.9830≈0.55。第二,相较于老年期的消费,参数θ反映了劳动者更偏好退休闲暇的程度,参照Goraus[21]的做法将θ赋值为0.588。第三,参数σ表示劳动者关爱子女程度,参照景鹏[22]的做法设定σ=0.195。第四,参照Becker[19]的做法,设定教育部门生产率参数d=6。第五,参数q反映了劳动者养育每个子女的物质成本占其工资收入比例,参照汪伟[18]的做法设定q=0.1。第六,就养育子女数量n而言,参照《国家人口发展规划(2016—2030年)》数据,我国2015年总和生育率为1.5左右,因为模型中劳动者(1人)代表一个家庭(夫妻2人),所以设定养育子女数量n=1.5/2=0.75个。第七,就老年期生存概率π而言,模型中老年期时间跨度为30年,由《“十四五”国民健康规划》可知2020年我国人均预期寿命接近78岁,平均退休年龄约56岁,退休后剩余寿命为22年,因此老年期生存概率π=22/30≈0.733。第八,参照汪伟[18]的做法,设定物质资本产出弹性α=0.45,生产技术水平参数A=10。
2.数值模拟应注意的问题。第一,数值模拟中要确保养老保险基金收入等于支出,也就是要使养老保险基金收支平衡方程式(10)成立。养老保险基金收入仅来源于成年期和老年期的劳动者缴纳的养老保险费,不包括政府财政补贴。因此在没有财政补贴的条件下,政府可通过调整退休年龄、缴费比例和养老金替代率实现养老保险基金收支平衡。第二,关于缴费比例τ的取值范围问题。国务院办公厅2019 年发布的《降低社会保险费率综合方案》把养老保险单位缴费比例下调为16%,个人仍为8%,所以当前缴费比例为16%+8%=24%。既有研究[18,23]表明养老保险缴费比例合理区间为10%~22%,所以本文把缴费比例区间设置为10%~24%。第三,因为效用函数单调性变换不影响劳动者决策行为,所以进行数值模拟时设定初始劳动者人力资本存量h1=1。第四,在养老保险基金收支平衡条件下,关于缴费比例τ和替代率r两者关系的处理方法如下:首先,构建缴费比例和替代率的各种组合,构建过程中缴费比例和替代率两参数步长分别设为1%和0.1%,替代率取值范围为10%~60%;其次,根据动态一般均衡的参数表达式求出稳态下的教育子女投入时间e*、老年劳动供给时间l*、劳动者终身福利水平U*;最后,如果在稳态下缴费比例与替代率的组合导致养老保险基金盈余或赤字,那么根据养老保险基金收支平衡原则剔除这些组合。
(二)弹性延迟退休制度的数值模拟结果分析
根据稳态下各变量的参数表达式与参数取值,本文可得出相应的数值模拟结果。
第一,弹性延迟退休制度提高了养老金替代率。图1 为弹性延迟退休制度对养老金替代率的影响,如图1 所示给定养老保险基金收支平衡条件,在弹性延迟退休制度下,无论哪个养老保险缴费比例所对应的养老金替代率都始终高于当前退休制度下的养老金替代率。对这个数值模拟结果的解释如下:首先,相较于当前退休制度而言,弹性延迟退休制度延长了劳动者在老年期的劳动供给时间,从而提高了养老保险基金收入;其次,老年期劳动供给时间的延长会导致劳动者退休后养老金计发月数缩短,从而使各月养老金收入增加。这两方面作用表明如果政府实施弹性延迟退休制度,那么在养老保险基金预算平衡条件下会提高养老金替代率。
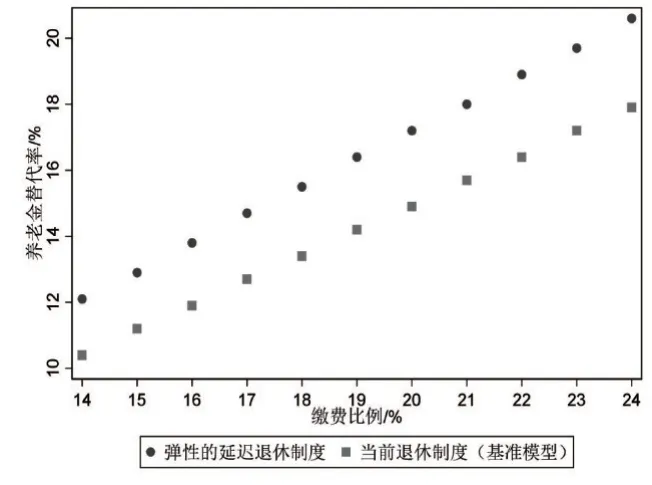
图1 弹性延迟退休制度对养老金替代率的影响
值得注意的是,图1中模型拟合的当前退休制度下的养老金替代率是实际情况的极端值。如图1所示给定养老保险基金收支平衡条件下,现阶段养老保险缴费比例24%对应的模型拟合养老金替代率为17.9%,而根据国家统计局2020年数据,我国养老金替代率为41.27%。两者之间差距较大的原因在于:首先,本文在计算养老保险基金收入时未纳入政府财政补贴,从而导致模型的养老保险基金收入低于实际情况;其次,模型中老年人口抚养比并未考虑到现实人口结构,从而使模型中人口老龄化程度高于实际情况。由于模型中以1 个代表性劳动者作为分析对象并且养育子女数n=0.75 个,这导致老年人口抚养比为1/0.75≈1.33,而根据第七次全国人口普查数据我国老年人口抚养比为0.295,远低于模型取值。以上两方面因素导致模型拟合的养老金替代率低于实际情况,由此可知模型拟合的养老金替代率是在老龄化程度比较高和缺乏财政补贴的极端不利条件下得出的,因此模型拟合结果是实际情况的极端值。
第二,弹性延迟退休制度导致劳动者终身福利水平下降,这主要归因于弹性延迟退休制度降低了劳动者成年期消费水平。图2为弹性延迟退休制度下劳动者福利变化情况,如图2所示无论在哪个养老保险缴费比例下,相较于当前退休制度而言弹性延迟退休制度导致的劳动者效用变化量均为负数,这表明劳动者终身福利水平下降。由劳动者终身福利构成要素可知:首先,弹性延迟退休制度延长了老年劳动供给时间,这会挤压退休闲暇时间从而导致劳动者退休闲暇效用下降(图2中退休闲暇效用变化量为负数);其次,弹性延迟退休制度虽然降低了劳动者成年期消费但是提高了老年期消费,从而导致这两期消费对劳动者终身福利水平的作用完全相反;最后,子女人力资本增加虽然提高了劳动者终身福利水平但是作用较小。一方面弹性延迟退休制度提高老年期消费所获得的效用增量与缩短退休闲暇时间所造成的效用损失量相当,另一方面弹性延迟退休制度下子女人力资本增加所带来的效用增量较小,由此可知弹性延迟退休制度下劳动者终身福利损失主要归因于成年期消费的下降,如图2所示成年期消费导致的福利损失量与劳动者福利损失量基本重合。
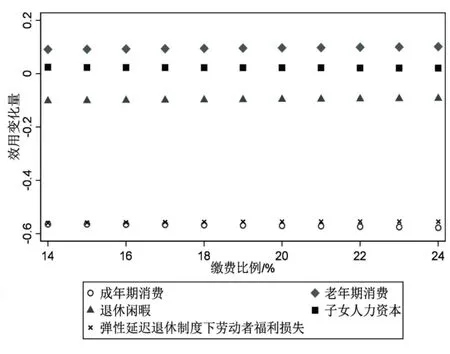
图2 弹性延迟退休制度下福利变化量
第三,弹性延迟退休制度下劳动者会增加教育子女的投入时间,养老保险缴费比例越低越有利于提高子女人力资本水平。本文的世代交叠模型假定成年期1 单位时间禀赋对应的时间跨度为30 年,用模型拟合的教育子女投入时间乘以30 可转化为以年为单位的投入时间,具体如图3 所示。可知在弹性延迟退休制度下劳动者教育子女的最优投入时间为3.94~3.98年,而当前退休制度下最优投入时间为3.66 年且不受养老保险缴费比例的影响。图3 右坐标表明在弹性延迟退休制度下,养老保险缴费比例越低则劳动者教育子女的投入时间增量越大,从而越有利于提高子女人力资本水平。
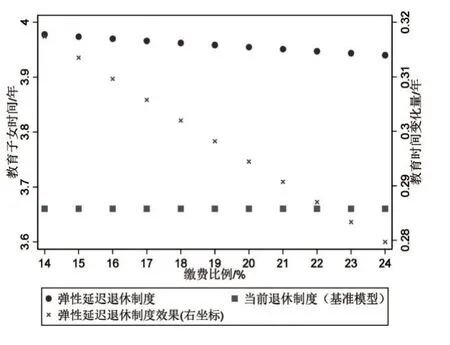
图3 弹性延迟退休制度下教育子女投入时间
第四,给定养老保险基金收支平衡条件,弹性延迟退休制度下退休年龄、养老保险缴费比例、养老金替代率三者之间是协同调整的关系。在弹性延迟退休制度下劳动者决策行为的拟合结果如表1所示,可知当养老保险缴费比例为24%时,政府为实现养老保险收支平衡所确定的养老金替代率为20.6%。模型拟合结果表明劳动者为追求终身效用水平最大化愿意把老年期1 单位时间禀赋的32.37%用于工作,又由参数取值中老年期的生存概率π=0.733 和老年期时间跨度30 年可知劳动者在老年期愿意付出的劳动供给时间为32.37%×0.733×30≈7.12 年,再结合当前实际平均退休年龄56 岁可得弹性延迟退休制度下劳动者退休年龄为63.12岁。
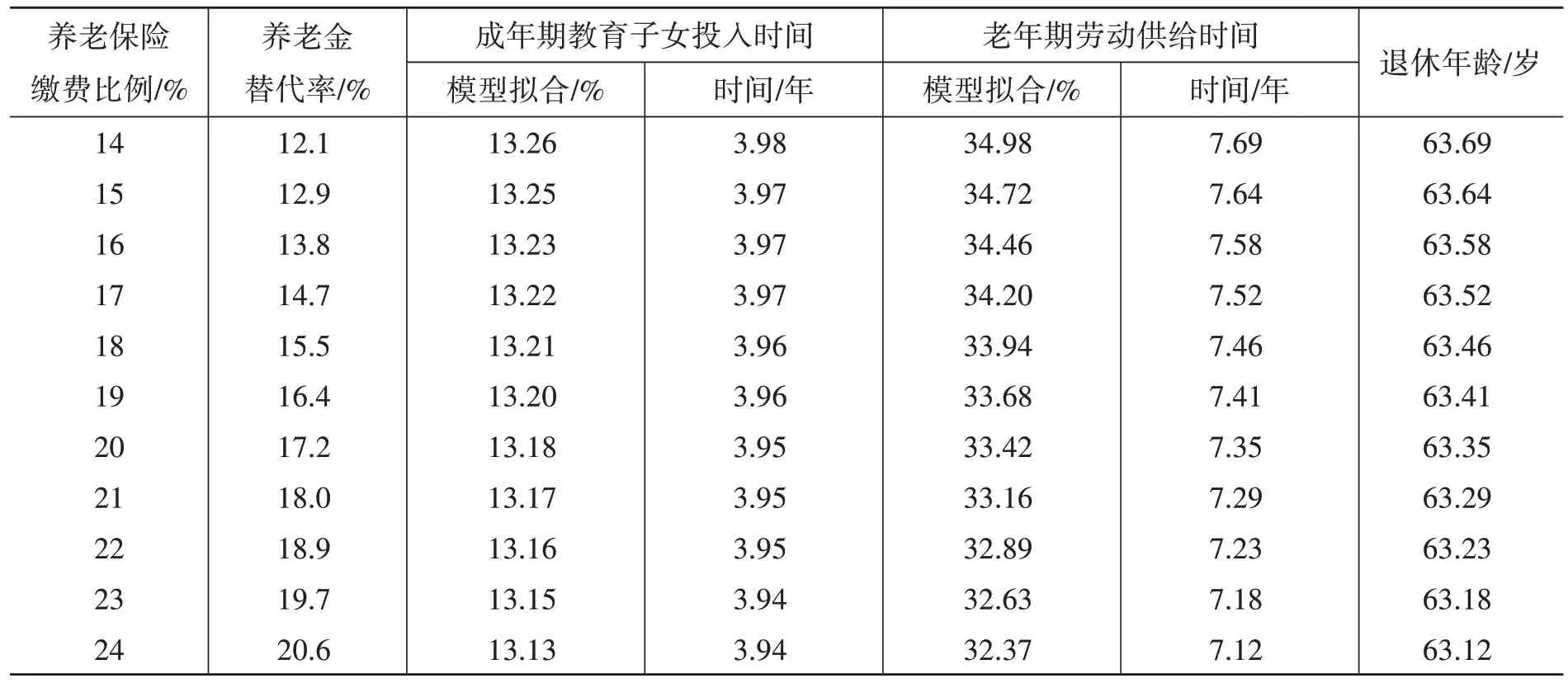
表1 弹性延迟退休制度下劳动者决策行为拟合结果
由表1 可知,在弹性延迟退休制度下,如果政府逐渐降低养老保险缴费比例,那么为了实现养老保险基金收支平衡就要下调养老金替代率。在此过程中劳动者根据终身效用最大化原则,不但会逐渐增加教育子女的投入时间而且会延长老年劳动供给时间。由此可知,弹性延迟退休制度下实现养老保险基金收支平衡是退休年龄、养老保险缴费比例、养老金替代率三者协同调整的结果。综上所述,政府逐渐降低养老保险缴费比例不但有助于延长老年劳动供给时间,而且有助于提高劳动者子女人力资本水平,这将有助于持续提升国民人力资本存量。
(三)弹性延迟退休制度下劳动者异质性分析
前文以当前退休制度为基准,分析了弹性延迟退休制度下代表性劳动者教育子女的投入时间和老年劳动供给时间的变化情况。下文以此为基础分析劳动者异质性对子女人力资本投资和老年劳动供给的影响,主要关注以下4个方面的异质性:劳动者生育子女数量、劳动者在老年期的生存概率、劳动者偏好退休闲暇的程度、劳动者关爱子女程度。
1.关于劳动者生育子女数量异质性的分析。《国家人口发展规划(2016—2030年)》数据显示,我国2015年总和生育率为1.5左右,因而前文进行模型拟合时设定1个代表性劳动者生育子女数量为0.75个,这表明代际之间人口数量是在减少的。模型中没有考虑到代际之间人口数量相同和人口数量增加两种情况,因此本文拟合了生育子女数量分别为1个和1.25个的两种情况,模型拟合结果如图4~图6所示(图中缺失的点是因为在该缴费比例下动态一般均衡无解)。
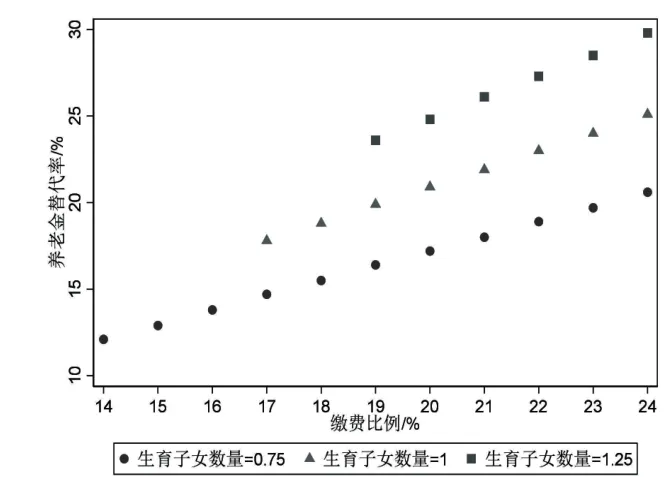
图4 生育子女数量与养老保险收支平衡
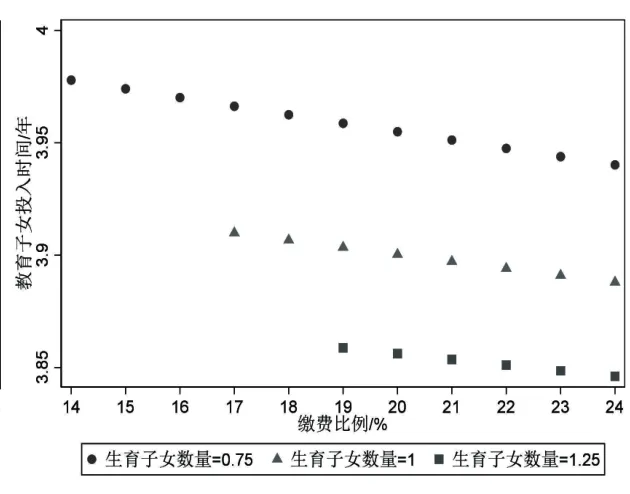
图5 生育子女数量与教育子女的投入时间
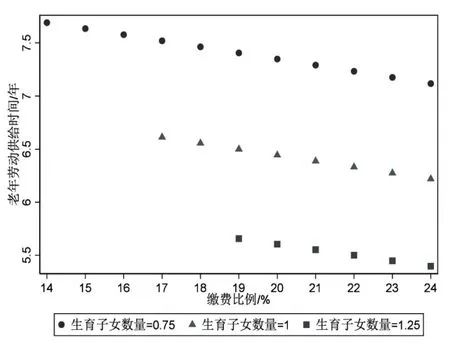
图6 生育子女数量与老年劳动供给时间
具体而言:一方面,劳动者生育子女数量越多养老保险收支平衡下的养老金替代率越高。以当前养老保险缴费比例24%为例,如图4所示,在弹性延迟退休制度下当劳动者生育子女数量为0.75个时对应的养老金替代率为20.6%,当生育子女数量为1个即代际之间人口数量相同时对应的养老金替代率为25.1%,当生育子女数量为1.25个即代际之间人口数量增加时对应的养老金替代率为29.8%。另一方面,生育子女数量越多劳动者教育子女的投入时间越少、老年劳动供给时间越短则退休年龄越低。以当前养老保险缴费比例24%为例,如图5所示,在弹性延迟退休制度下当劳动者生育子女数量依次为0.75 个、1 个、1.25 个时,所对应的劳动者教育子女的投入时间依次为3.94 年、3.88 年、3.83 年,在其他养老保险缴费比例下投入时间也都是递减的,这表明生育子女数量越多劳动者教育子女的投入时间越少。同样,以当前养老保险缴费比例24%为例,如图6 所示当劳动者生育子女数量依次为0.75 个、1 个、1.25 个时,所对应的老年劳动供给时间依次为7.12 年、6.22 年、5.4 年,在其他养老保险缴费比例下老年劳动供给时间也都是递减的,这表明生育子女数量越多劳动者的老年劳动供给时间越短则退休年龄越低。
2.关于劳动者预期寿命异质性的分析。前文参数取值中生存概率参数值为0.733,是由退休后剩余寿命22 年除以老年期时间跨度30 年所得的,由此可知劳动者预期寿命越长则退休后剩余寿命越长,劳动者在老年期的生存概率就越高,因此本文还拟合了老年期生存概率为0.833和0.933的两种情况,模型拟合结果如图7~图9所示(图中缺失的点是因为在该缴费比例下动态一般均衡无解)。

图7 预期寿命与养老保险收支平衡
具体而言:一方面,在养老保险收支平衡条件下,劳动者预期寿命越长则养老金替代率越低。以当前养老保险缴费比例24%为例,如图7所示,在弹性延迟退休制度下当劳动者生存概率为0.733时,养老保险收支平衡对应的养老金替代率为20.6%。当生存概率为0.833 和0.933 时养老保险收支平衡对应的养老金替代率为18.5%和16.9%,同样在其他养老保险缴费比例下也表现为劳动者老年期生存概率越高养老金替代率越低,由此可知劳动者预期寿命越长则养老金替代率越低。另一方面,预期寿命越长则劳动者教育子女的投入时间越少、老年劳动供给时间越长,退休年龄越高。以当前养老保险缴费比例24%为例,如图8 所示,在弹性延迟退休制度下当劳动者老年期生存概率依次为0.733、0.833、0.933时,所对应的劳动者教育子女的投入时间依次为3.94年、3.83年、3.72年,在其他养老保险缴费比例下投入时间也都是递减的,这表明预期寿命越长劳动者教育子女的投入时间越少。同样,以当前养老保险缴费比例24%为例,如图9 所示,当劳动者老年期生存概率依次为0.733、0.833、0.933时,所对应的老年劳动供给时间依次为7.12年、7.96年、8.78年,在其他养老保险缴费比例下老年劳动供给时间也都是递增的,这表明预期寿命越长则劳动者老年劳动供给时间越长,退休年龄越高。
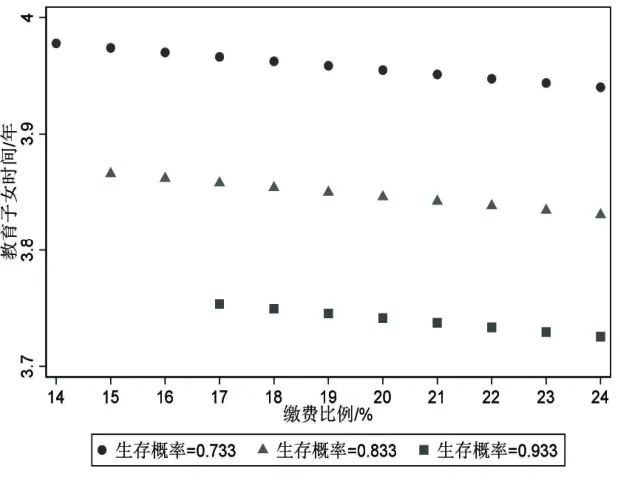
图8 预期寿命与教育子女的投入时间
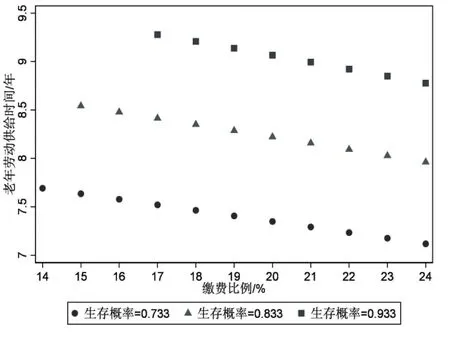
图9 预期寿命与老年劳动供给时间
3.关于劳动者退休闲暇偏好异质性的分析。前文参数取值中退休闲暇偏好的参数值为0.588,本文还拟合了退休闲暇偏好参数值为0.688和0.788的两种情况,模型拟合结果如图10~图12所示。
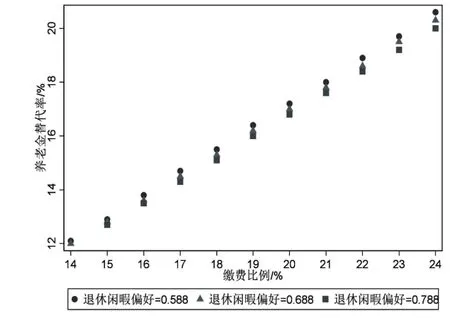
图10 退休闲暇偏好与养老保险收支平衡
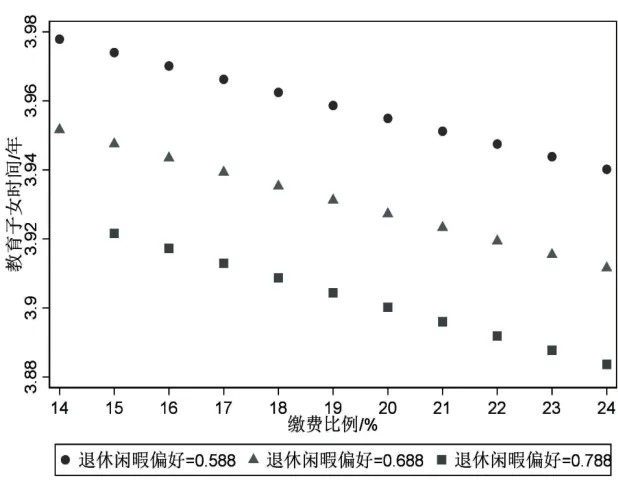
图11 退休闲暇偏好与教育子女的投入时间
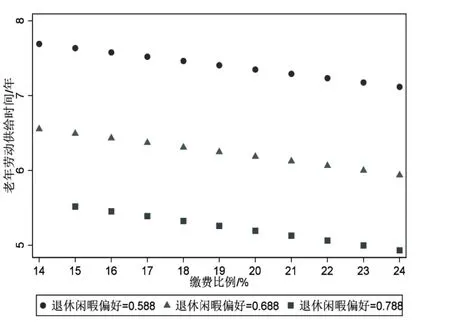
图12 退休闲暇偏好与老年劳动供给时间
具体而言:一方面,在养老保险收支平衡条件下,劳动者退休闲暇偏好程度越高则养老金替代率越低。以当前养老保险缴费比例24%为例,如图10所示,当退休闲暇偏好为0.588时养老保险收支平衡对应的养老金替代率为20.6%,当退休闲暇偏好为0.688 和0.788 时养老保险收支平衡对应的养老金替代率为20.3%和20%。同样,在其他养老保险缴费比例下也表现为退休闲暇偏好程度越高则养老金替代率越低,由此可知劳动者越偏好退休闲暇则养老金替代率越低。另一方面,退休闲暇偏好程度越高则劳动者教育子女的投入时间越少、老年劳动供给时间越短,退休年龄越低。以当前养老保险缴费比例24%为例,如图11所示,退休闲暇偏好依次为0.588、0.688、0.788时,所对应的劳动者教育子女的投入时间依次为3.94年、3.91年、3.88年,在其他养老保险缴费比例下投入时间也都是递减的,这表明退休闲暇偏好程度越高则劳动者教育子女的投入时间越少。同样,以当前养老保险缴费比例24%为例,如图12 所示,当退休闲暇偏好依次为0.588、0.688、0.788 时,所对应的老年劳动供给时间依次为7.12年、5.93年、4.93年,在其他养老保险缴费比例下老年劳动供给时间也都是递减的,这表明退休闲暇偏好程度越高则老年劳动供给时间越短,退休年龄越低。
4.关于劳动者关爱子女程度异质性的分析。前文参数取值中劳动者关爱子女程度的参数值为0.195,本文还拟合了劳动者关爱子女程度参数值为0.225和0.255的两种情况,模型拟合结果如图13~图15所示。
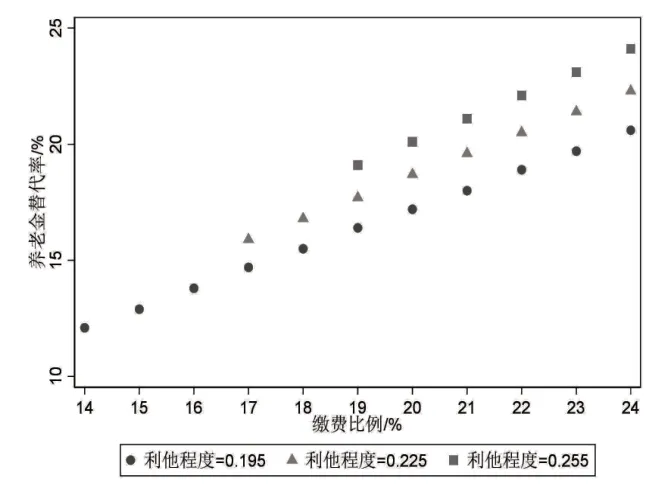
图13 关爱子女程度与养老保险收支平衡

图14 关爱子女程度与教育子女的投入时间
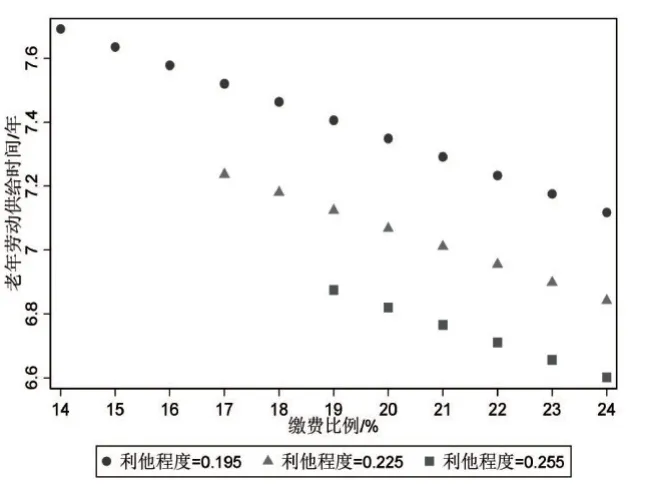
图15 关爱子女程度与老年劳动供给时间
具体而言:一方面,在养老保险收支平衡条件下,劳动者关爱子女程度越高则养老金替代率越高。以当前养老保险缴费比例24%为例,如图13所示,当劳动者关爱子女程度参数值为0.195时养老保险收支平衡对应的养老金替代率为20.6%,当劳动者关爱子女程度参数值为0.225 和0.255 时养老保险收支平衡对应的养老金替代率为22.3%和24.1%。同样,在其他养老保险缴费比例下也表现为劳动者关爱子女程度越高则养老金替代率越高,由此可知劳动者越关爱子女则养老金替代率越高。另一方面,劳动者关爱子女程度越高则劳动者教育子女的投入时间越多、老年劳动供给时间越短,退休年龄越低。以当前养老保险缴费比例24%为例,如图14 所示,劳动者关爱子女程度参数值依次为0.195、0.225、0.255时,所对应的劳动者教育子女的投入时间依次为3.94年、4.44年、4.92年,在其他养老保险缴费比例下投入时间也都是递增的,这表明劳动者关爱子女程度越高则劳动者教育子女的投入时间越多。同样,以当前养老保险缴费比例24%为例,如图15所示,当劳动者关爱子女程度参数值依次为0.195、0.225、0.255时,所对应的老年劳动供给时间依次为7.12年、6.84年、6.6年,在其他养老保险缴费比例下老年劳动供给时间也都是递减的,这表明劳动者关爱子女程度越高则老年劳动供给时间越短,退休年龄越低。
五、结论与建议
人口老龄化加速背景下政府提出了“实施渐进式延迟法定退休年龄”的政策目标,本文运用世代交叠模型,从子女人力资本投资和老年劳动供给视角分析了在延迟退休改革中引入弹性退休制度对劳动者决策行为的影响。研究发现:第一,虽然弹性延迟退休制度提高了养老金替代率,但是降低了劳动者终身福利水平,这主要归因于弹性延迟退休制度降低了劳动者成年期消费;第二,弹性延迟退休制度下劳动者会增加教育子女的投入时间,政府调低养老保险缴费比例不但能提高子女人力资本水平而且有助于延长老年劳动供给时间;第三,劳动者生育子女数量、预期寿命、退休闲暇偏好、关爱子女程度4个方面的异质性都会影响劳动者关于子女人力资本投资和老年劳动供给的决策行为。
对此,本文提出如下政策建议:第一,延迟退休改革中应该引入弹性退休制度,这样劳动者可根据个人情况选择合适的退休年龄,这种制度安排既延迟了退休年龄又降低了劳动者福利损失,不仅有利于延迟退休改革政策顺利实施,还有利于社会和谐稳定;第二,要拓宽养老保险基金收入来源渠道。本文研究发现仅依靠劳动者缴纳养老保险费实现的养老金替代率较低,为增加养老保险基金收入,要厘清各级政府财政补贴养老保险基金的责任,加快完善国有资本充实社保基金制度并尝试建立社保基金捐赠接收制度,鼓励社会各界向社保基金捐款;第三,政府不但要调低养老保险缴费比例而且要完善多支柱养老保险体系。虽然调低养老保险缴费比例降低了养老金替代率,但是其既能提高子女人力资本水平又能延长老年劳动供给时间,因此可以通过完善多支柱养老保险体系来填补养老保险缴费比例下调导致的养老金损失。

