层状全空间介质中重叠回线的瞬变电磁响应

刘建鹏, 车海清, 朱 华, 刘 飞, 孙 岩

(核工业二九〇研究所, 广东 韶关 512029)

地面瞬变电磁法是发射和接收装置均位于地面的时间域方法,接收回线中得到随时间衰减的感应电动势,能有效地反映该点竖直深度方向的电性特征[1-3]。但随着复杂环境的地质勘探任务需求增加,特别是在工程隧道、煤炭巷道超前探测、全空间地质灾害等方面,全空间瞬变电磁法具有勘探效率高、对低阻体灵敏和无须接地等优点,全空间瞬变电磁法已经成为首选的地球物理方法,并逐渐成为矿井勘探领域研究的热点[4-9]。尤其受工作条件等因素限制,重叠回线装置应用较为广泛。

伴随着煤炭等非金属矿的开采和交通运输的开发,国内已经取得了许多的研究成果。部分研究通过物理实验的方法,探究出重叠回线的分辨率和信号强度主要跟发射回线参数有关,并利用等磁矩的方式将多匝回线等效为同等面积的大半径回线,得出小回线装置同样具有较大的探测深度[10-12]。理论研究则根据电磁场原理,结合数理方面已经能模拟多维瞬态扩散场,而对于一维瞬态扩散场研究较缓,与传统磁偶源理论不同,可通过研究层状海洋模型的回线源解析解,来探究全空间与半空间瞬变电磁法的联系与区别[13-22]。

从电磁场扩散原理出发,研究全空间中回线源产生的瞬变电磁场,分析了直接求解的响应和柱坐标下求解的响应表达式,并利用贝塞尔函数的积分式将这两种解进行了统一,推导了层状全空间重叠回线的响应和计算方法,从而探究发射半径对全空间瞬变电磁场的影响规律。将该计算方法应用于实测矿井数据中,经拟二维断面分析,计算结果证实了方法的有效性。

1 均匀全空间的求解

1.1 直角坐标系下的求解

如图1所示,在电导率为σ、磁导率为μ0的均匀全空间中,存在一个发射电流为I、半径为r的重叠回线,在t时刻的感应电压为[3]

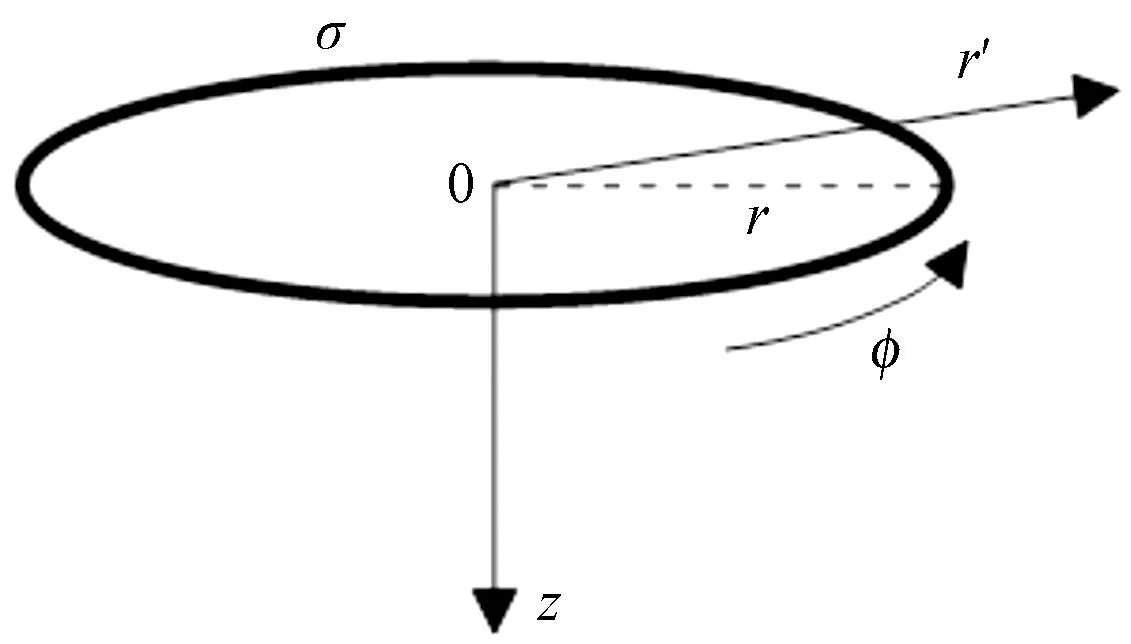
图1 全空间中的回线源

(1)

式中:

(2)

式中:R为观测点到原点的距离,R=2rsin(φ/2)。则式(2)为

(3)

式(1)变为

(4)

考虑第一类修正的贝塞尔的积分表达式[18],令v=1有:

(5)

结合式(4),则可以得到感应电压表达式为

(6)

1.2 柱坐标系下的求解

如图1所示,在柱坐标系(r′,φ,z)下,回线源的中心处为坐标原点(0,0,0),参数与图1一致,得到的水平方向电场为[14]

(7)

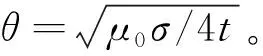
利用法拉第电磁感应定律,得

V(t)=∮Eφ

(8)

将(7)式代入(8)式中,则有

(9)

对比式(6)和式(9)可知,两种方法得出的感应电压完全相同,其中u1=θr,两者可以相互验证。

2 全空间层状介质的响应计算方法

如图2所示,建立全空间层状模型,Ti、Tj分别为第i层、j层的厚度(i=1,2,…,N-1,N;j=1,2,…,M-1,M);σi、σj分别为第i层、j层的电导率;半径为r的水平重叠回线源位于薄层中(层厚非常小,可忽略影响),拉普拉斯域下瞬变电磁感应电压为[13]。

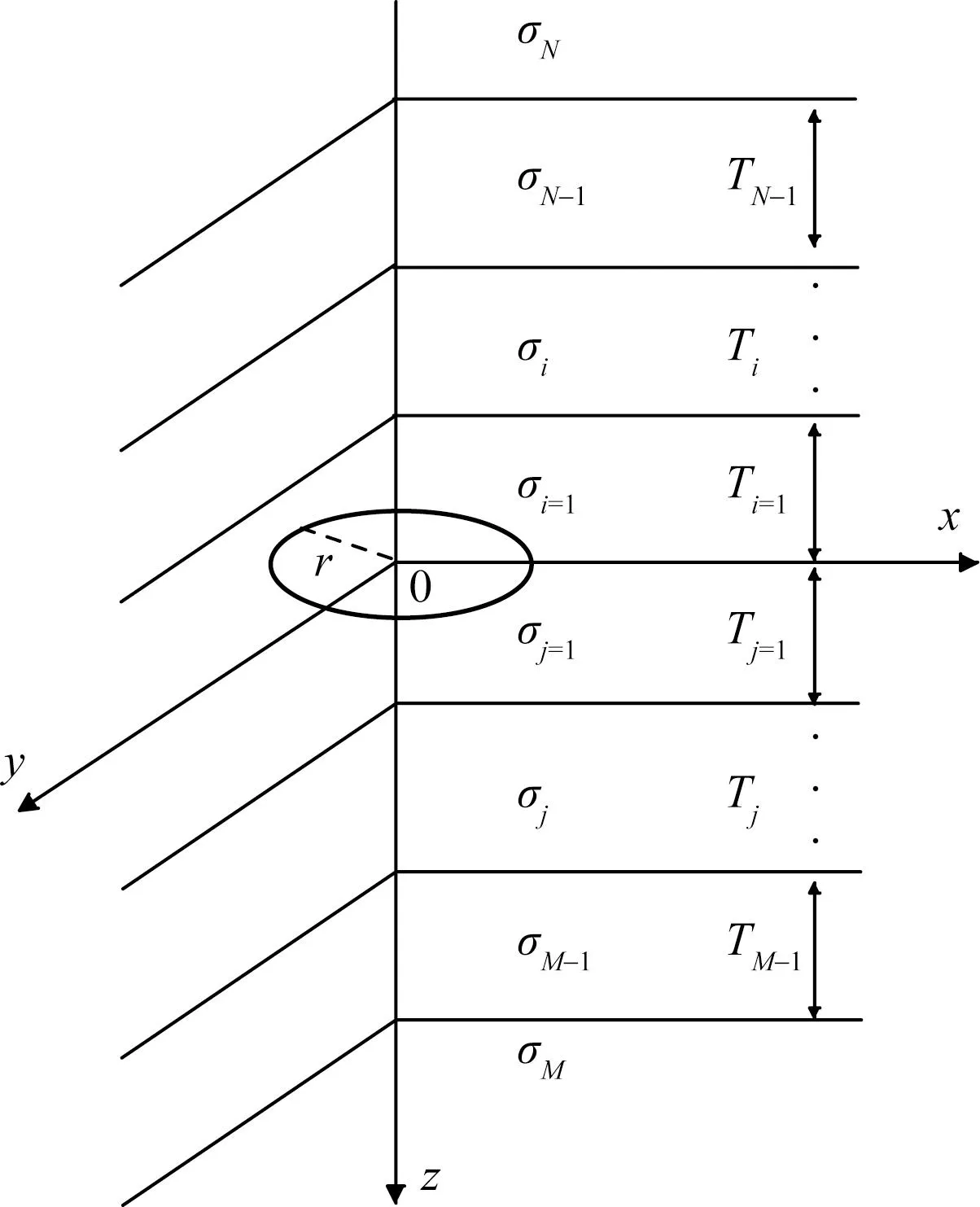
图2 位于层状介质中的重叠回线

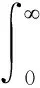
(10)

式中:s为拉普拉斯变量,s与F(λ)有关;J1为第一类一阶贝塞尔函数;磁矩m=Iπr2。其他参数与图1一致,F(λ)的推导公式为

(11)

式中:P、Q为每个层位之间的递推值;Ki=λ2+sμ0σi,Kj=λ2+sμ0σj;Ki、Kj为第i层、j层的波数。

递推的关键步骤是得到末端层的P、Q值,即当i=N、j=M时有Qi=N=μ0/Ki=N,Pj=M=μ0/Kj=M。即波数为Ki=N=λ2+sμ0σi=N,Kj=M=λ2+sμ0σj=M。

由上述可知,求解全空间重叠回线瞬变电磁响应的算法步骤为:从上下末端层(第N层,第M层)开始,逐步往中间递推,得到相应第一层的P1、Q1,代入式(10),最终经拉普拉斯逆变换得到时间域感应电压为

(12)

式中:L-1为拉普拉斯逆变换。与常规的地面瞬态响应计算方法相同,式(12)可联合汉克尔变换和正余弦变换得到时间域的瞬态响应[19-20]。

3 瞬变电磁响应规律

3.1 均匀全空间瞬变电磁场扩散规律

根据全空间瞬变场的扩散规律,回线源关断后产生的瞬变电磁场为水平方向的电场[9](后称为电场),研究电场在空间上的变化规律能直观地了解场的扩散特征。由式(7)可知,考虑一个垂直于φ平面且包含回线轴线的平面,该平面有利于直观展示瞬变电磁场随延时时间的扩散规律。另一方面,为研究电场在r方向、z方向的传播规律,可以给定一个半径r(m)或者深度z(m),得到电场在深度或者半径上的变化特征。

如图3所示,水平回线源在0.3 ms、1 ms和3 ms时的电场分布,其半径为40 m,全空间电导率为1/100 S/m,回线中的电流为3 A。在均匀全空间介质中,二次场的扩散规律依然满足“烟圈效应”,并且“烟圈”会在x轴、z轴方向上运动,而电场极值中心位置保持在r轴上。另外,电场的扩散形态并非规则的圆形,说明在瞬态场在空间中传播存在一定的方向性,不同方向的速度不同。在不均匀介质中,受+z、-z、+r方向的共同作用,似椭圆的电场将变得不光滑、不对称,受地下结构复杂多变的影响,满足扩散方程的电场形成更复杂的扩散,难以判断引起电场变化的异常来自+z还是-z方向。

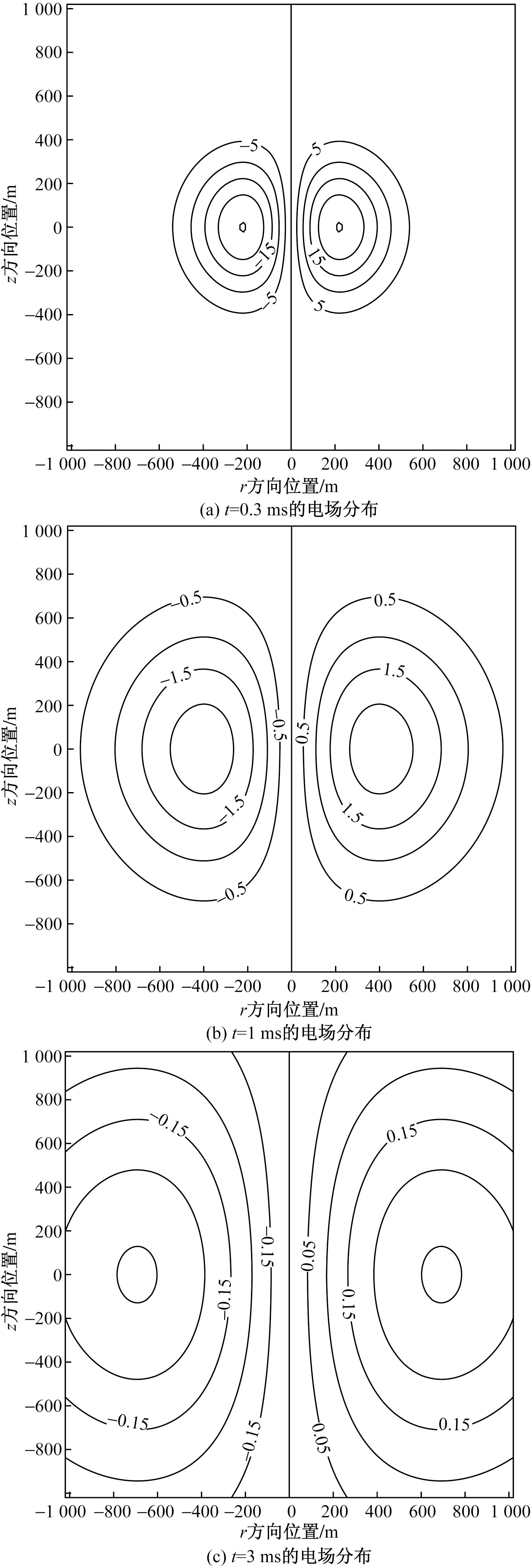
图3 全空间介质不同时刻的电场分布

3.2 全空间响应验证

回线半径是重叠回线的重要参数,决定了发射、接收回线的几何尺寸和磁矩。考虑半径对应电压的影响,建立半径分别为2、4、10、20、40、80、200 m的均匀全空间模型,同时为检验全空间层状解的精确性,利用相同参数的层状解来计算均匀介质,并呈现半径为4 m时的相对误差曲线。由图4可知,对于归一化感应电压而言,均匀全空间响应曲线形态基本相同;结合式(6)和式(9)对延时时间t的两个极限状态(早期t→0,晚期t→∞),在早期的响应遵循t-1衰减,经过渡期,晚期响应遵循t-5/2衰减;半径对早期的幅值影响大,将Kaufman[3]中的早期响应进行归一化,可得到响应与半径成反比关系,例如在半径为80和200 m时,前者的早期响应大于后者,到晚期则相反。另一方面,如图4和表1所示,层状解的响应相对误差较大值分布在延时时间始末时段,且相对误差都在4%以内,说明算法有效且较准确。

表1 不同半径的平均相对误差

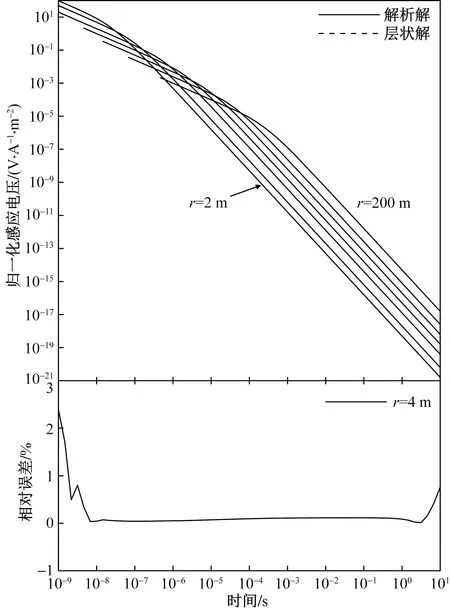
图4 不同半径尺寸的解析解和层状解

4 瞬变电磁响应特征

4.1 典型全空间响应特征

上文已经讨论尺寸对均匀全空间的影响,得出计算的层状解具有较高的精确度,为研究尺寸与层状介质响应的影响规律提供了基础。建立全空间的四层模型,发射回线的上半空间为均匀介质,下半空间为类似地面的H型,通过Swidinsky[21]分别得到全空间瞬态响应以及晚期视电阻率,如图5所示。

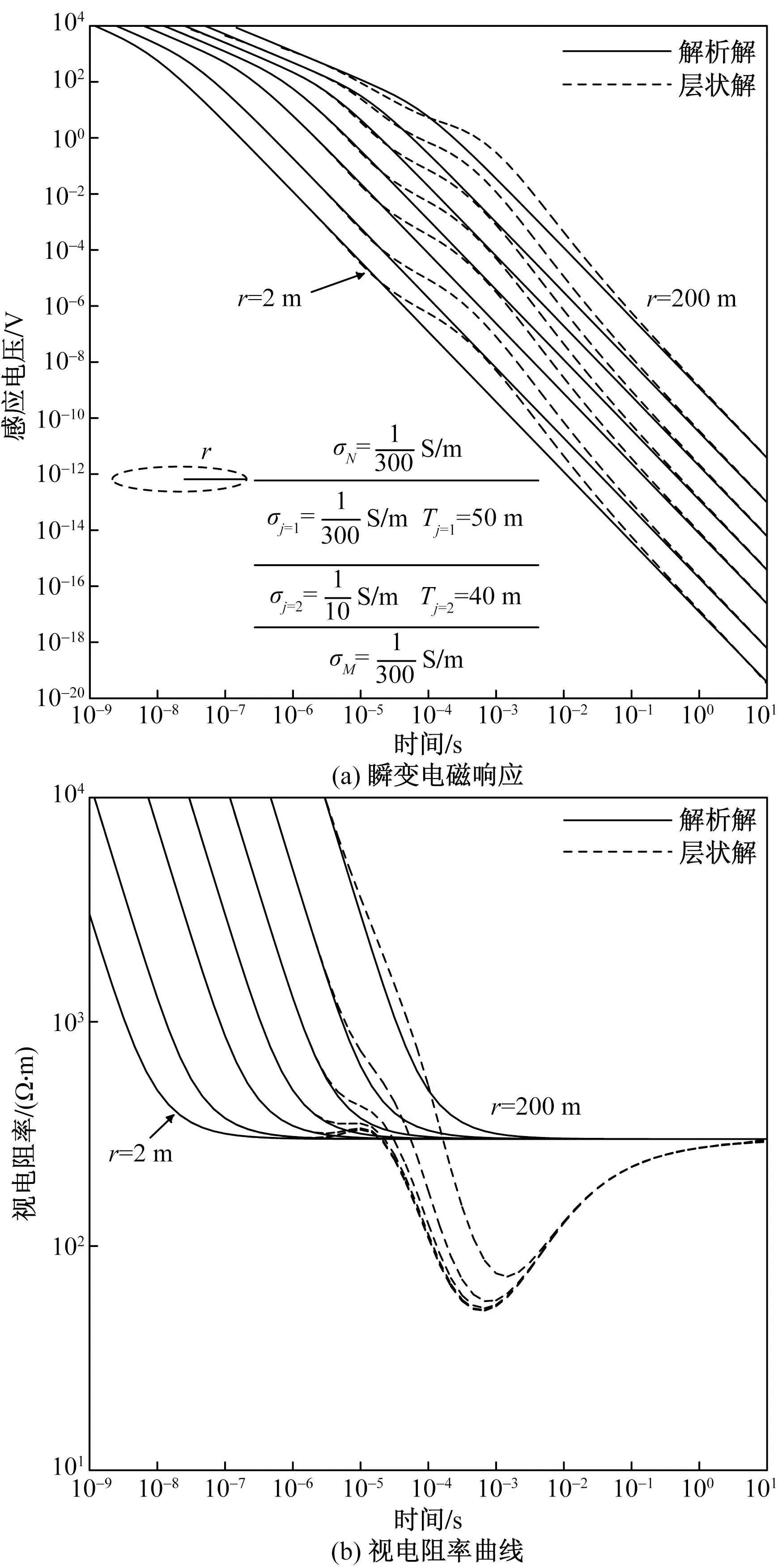
图5 四层全空间不同半径尺寸的响应和视电阻率曲线

由图5(a)可知,对比均匀全空间,回线半径小于层厚时,层状解响应脱离均匀解析解的时间基本一致;反之,则随半径的增加而延后,但其尾支形态的“回归时间”是一致的。“早期”响应的强度不随回线源半径的改变而改变,仅延时时间不同,即回线半径越大其低阻引起的响应时间越延后。另一方面,延时时间在0.1～100 ms时,通过增加回线源的半径能显著地增大响应值,进而提高响应的信噪比,这段时间正是矿井瞬变电磁数据采集的主要测量时间段,例如延时时间为1 ms时,半径从2 m增加到200 m,层状解感应电压从5.02×10-9V增加到0.30 V。由图5b可知,均匀全空间的晚期视电阻率应用范围随半径的增加而延后;当发射半径大于等于目标层厚度时,晚期视电阻率上移,不利于晚期各个公式的应用。

考虑一个较为典型的七层模型,下半空间地电参数保持不变,上半空间与下半空间关于发射层对称,即σi=1=σj=1=1/300 S/m,σi=2=σj=2=1/10 S/m,σN=σM=1/300 S/m,仅中间夹有空气层,其厚度为4 m,其他参数与图5一致。同样得到全空间瞬态响应以及对应的晚期视电阻率曲线,如图6所示。

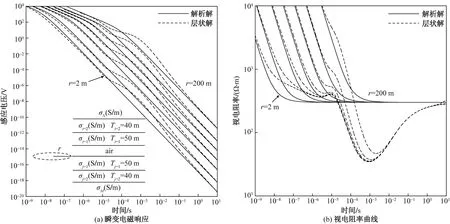
图6 七层全空间不同半径尺寸的(a)响应和(b)视电阻率曲线

由图6(a)可知,上半空间的变化,对于小尺寸的早期影响比较大,说明空气层作为一种真实存在的影响因素,不能直接忽略,这与实际应用中的结果一致。另一方面,受电磁波传播的对称性,上半空间低阻层的表征基本与下半空间重合,其响应表现在同一时段且叠加后的强度更大,但是不改变层状解脱离均匀解析解的延时时间,仅对表征响应的结果分析无法判断低阻层来自上半空间或者下半空间,与前文结果相同,这正是全空间效应的表现形式之一。由图6(b)可知,半径越小,巷道的影响越明显,但对于薄层的巷道不影响目标层的表征。

4.2 不同尺寸多层全空间响应特征

在考虑装置半径对响应的影响时,可以换一个角度:在改变层位中覆盖层、低阻层层厚的条件下,探讨相同半径在不同层厚尺度时对响应的影响,即半径为40 m,厚度分别为2、4、10、20、40、80、200 m及∞。图7、图8分别为不同层厚下的全空间响应和视电阻率结果。综合这些响应结果可以得出:随着低阻层层厚小于、等于到大于半径改变时,全空间瞬变电磁响应对异常持续时间越长,偏离解析解的程度越明显;随着异常体离发射位置越来越远,视电阻率也越 “偏离”真实值,且值偏大。

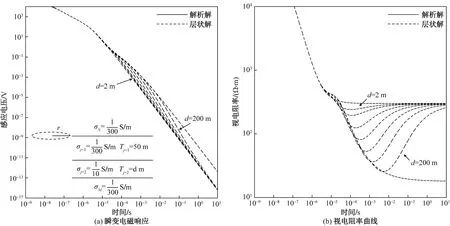
图7 四层全空间不同低阻层层厚尺寸的(a)响应和(b)视电阻率曲线

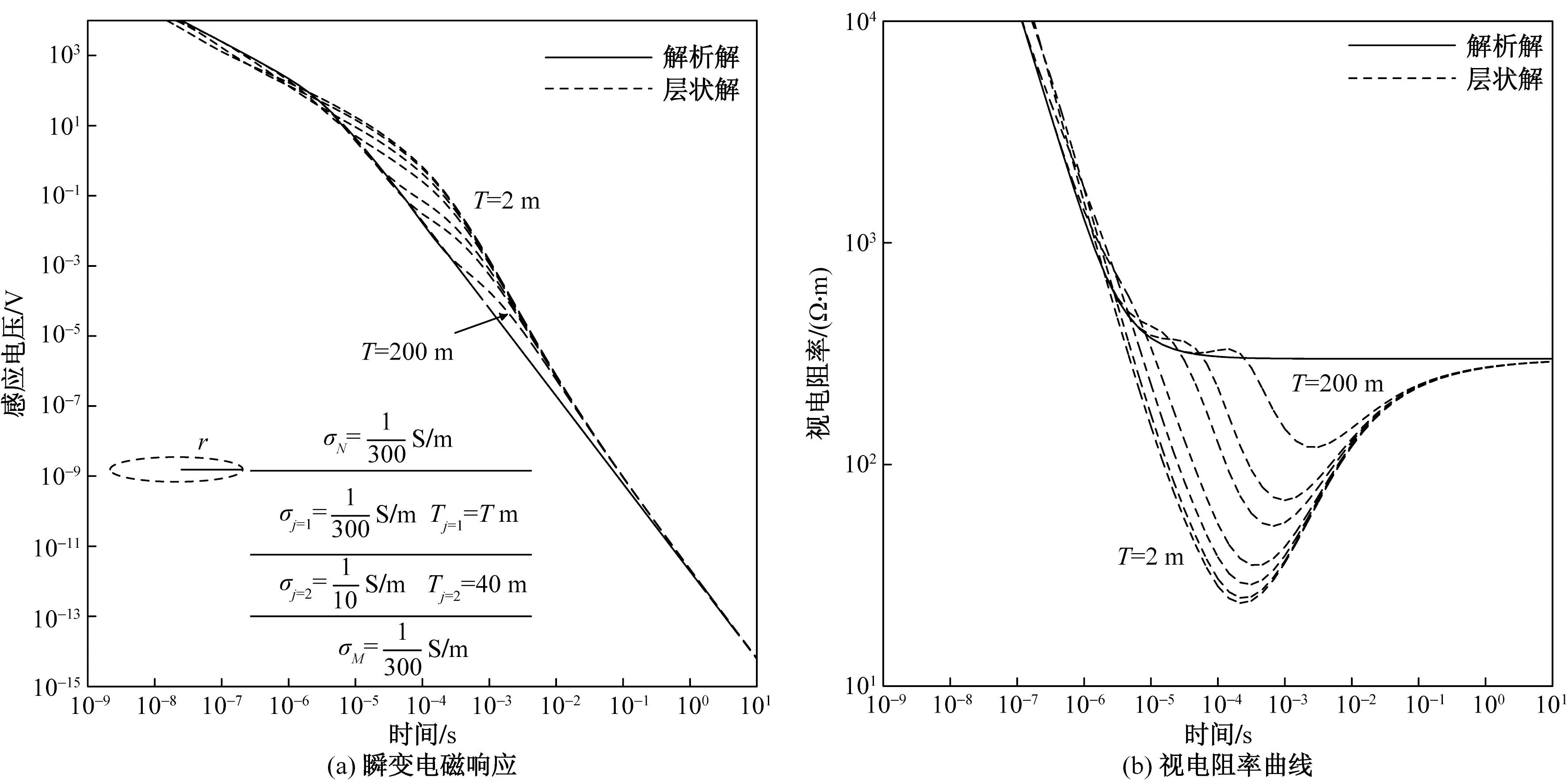
图8 四层全空间不同覆盖层层厚尺寸的(a)响应和(b)视电阻率曲线

5 应用实例

湖南省内煤矿众多,为了解某煤矿开采中掘进面上顶板的矿体分布情况,利用重叠回线发射源的瞬变电磁法开展超前探测。图9(a)为实测数据的视电阻率断面图,视深度结果采用于景邨[23]提出的矿井瞬变电磁法时间-深度转换公式;视电阻率采用杨海燕等[24]提出的全区视电阻率计算公式。由图可知,该区域横向变化明显,在x轴上的35 m和50～80 m位置上存在相对的低阻体,且数值较煤矿而言相近,该区域存在煤的可能性大。在此基础上,建立了全空间模型,如图9(b)所示,在x轴上布置点距为4.4 m的测线,长度为110 m,测点的z方向为全空间层状结构,其他参数与采集装置相同。图9(c)为理论数据的视电阻率断面图。由图9可知,两个断面图结构上较为吻合,理论数据的视电阻率断面明显反映两个低阻异常体的位置和形态。断面结果说明采用研究介绍的方法得出的全空间响应能反映瞬态场在地下的扩散规律。

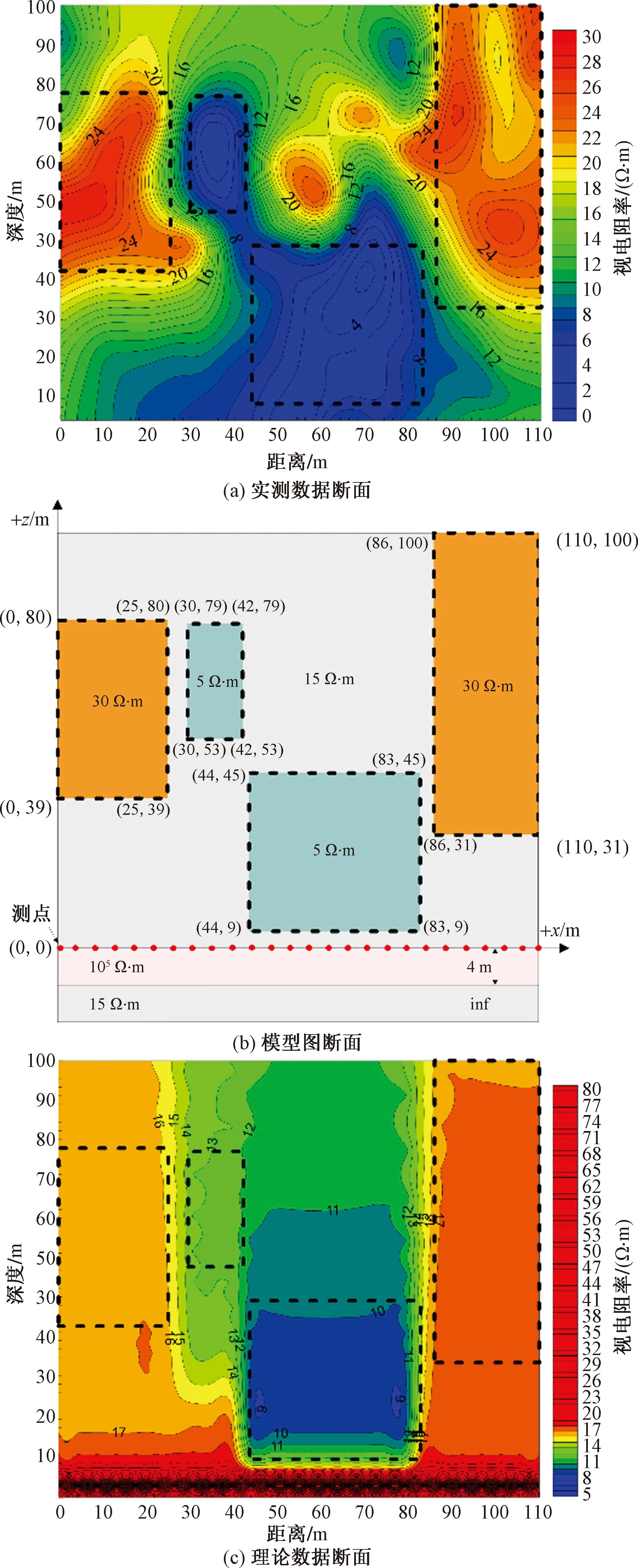
图9 实测数据断面、模型图断面和理论数据断面

6 结论

位于全空间中的回线源,通过直接计算和采用柱坐标系计算的方法能得出相同的瞬变电磁响应;并以此为基础,得到垂直平面上的水平方向电场,该电场呈椭圆状,证实回线源装置探测具有一定的方向性,同时这也构成了全空间瞬变电磁场难以分辨异常体位置的复杂性。

在不同半径条件下的瞬变电磁响应,相对“早期”响应,全空间响应与半径成反比,且按延时时间t-1衰减。

采用层状解公式计算的均匀全空间响应,具有相对误差较小和精度较高等特点,能够用来计算层状空间的瞬变电磁响应;在“早期”响应中,强度不随回线半径的变化而改变,只是延时时间不同,即回线半径越大响应时间越延后。在“晚期”响应中,通过增加回线源的半径能显著地增大响应值,可以提高地下瞬变电磁法的抗干扰性能。

对于全空间的晚期视电阻率应用范围,当发射半径大于等于目标层厚度时其视电阻率值上移,不利于晚期公式的应用。半径越小,巷道对早期响应的影响越明显,但其对目标层的表征影响较小。