结构力学位移法基本思想表述及课程思政映射与融入

蒲 爽，蔡继伦，陈方舟，郭丽娟，雷 阳，黄川腾*

（1.遵义师范学院工学院，贵州 遵义 563006；2.遵义职业技术学院建筑与艺术设计系，贵州 遵义 563006；3.中建四局第三建设有限公司，贵州 遵义 563006）

超静定结构是有多余约束的几何不变体系，因体系未知量（内力和多余约束）超过3 个，无法仅通过三个力平衡方程（式1）直接求解。力法和位移法是求解超静定结构的两种基本方法，其本质都是找寻新的方程，以便联合三个力平衡方程求解体系全部未知量，不同之处在于找寻平衡方程的基本思想不同。

如图1 所示，力法基于变形协调的基本思想，通过取消多余约束代以多余未知力将超静定结构转化为静定结构（即力法基本结构），针对每一个多余约束建立变形协调方程（即力法基本方程），变形协调方程表征的是基本结构在多余未知力和外荷载共同作用下引起的多余约束方向位移与原结构一致。

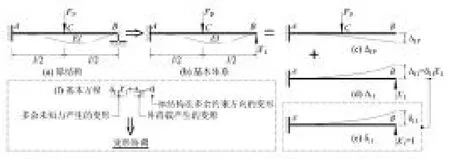
图1 力法基本思想的图解分析

力法基本思想和基本方程物理概念明晰，符合学生认知逻辑，其基本结构为静定结构，基本方程中主系数、副系数和自由项均通过图乘法计算，都是课程前面章节的学习重点，前后知识过渡连续、自然，学生掌握程度较好。但也应注意到，当求解具有个多余约束的超静定结构时，需至少完成(+3)/2 次图乘法，还需求解一个元1 次方程组；当较大且不能通过对称性简化结构时，计算工作量较大，甚至可能无法手算求解。位移法尤其适用于高次超静定结构的计算，而且是常用的渐近法（如力矩分配法、无剪力分配法）和适用于计算机计算的矩阵位移法的基础，在超静定结构力学领域，位移法有着承前启后的重要作用。

线弹性结构在荷载和非荷载作用下，其内力与位移之间具有确定的一一对应关系，意味着可以由内力计算位移或由位移计算内力，前者是力法的求解手段，后者是位移法的求解手段。龙驭球将力法和位移法比作“对联”[1]——形式相同、实质相异。在位移法讲授和学习时，往往将其与力法比照、模仿，这是高效的做法。但因为对“由力计算位移”的过程更熟悉，加之力法的基本未知量实际上与之前“结构几何组成分析”章节联系密切，力法显然更符合长久以来形成的思维定式，教与学都更加容易。由于缺少符合逻辑的、可解释的、统一的解题思路（或解题“想法”），位移法理解难度较大，导致教与学更多侧重在解题技法层面，忽视了力学逻辑和力学概念的构建。由于缺乏逻辑假设，在诸如“基本未知量选取”“基本方程建立”“弯矩图符号规定”等问题上，学生很难“知其所以然”。总体上，因为位移法基础概念多、建模思想理解难度大、常数记忆量大、符号定义复杂、知识过渡存在突变，造成教学效果较差，对此众多教师对位移法教学开展了大量研究与探讨。

（1）教学技巧方面

吴耀鹏[1]、李远瑛[2]和蔡长青[3]分别针对含刚性斜杆的平面有侧移刚架、带滑动支座斜杆刚架和具有剪力静定杆的超静定问题提出了计算的技巧。黄志刚[4]对位移法的基本思路和基本未知量的确定进行探析和归纳，深化了位移法“分解”+“叠加”的求解思路。赵志军[5]提出一种“复旧导新”的教学设计，引导学生从已掌握的力法方法，通过思考、类比分析来过渡到位移法的建立。徐丰[6]指出准确求得位移法基本方程中的刚度系数和自由项是学生运用位移法解题的难点，提出了一套避免刚度系数和自由项符号发生混乱的解题规则。

（2）教学手段方面

田振国[7]对力法、位移法、力矩分配法等超静定结构计算方法进行了归纳、梳理，便于有针对性地选取合理方法。阙仁波[8]提出以目标为导向，从总体到具体的“总体教育方法”，并以位移法为例展示了教学方法。邱秀梅[9]提出位移法教学时应与力法对应起来加以比较、总结、提炼，抽取两种方法的理论精髓，形成解法口诀便于学生掌握。李炜明[10]提出采用一题多解的手段对各种超静定结构计算方法、过程进行总结与比较，以便让学生掌握各种方法之间的联系与差异，有利于更为系统地掌握解法要点与技巧。

上述对位移法教学的探讨集中在教学技巧和教学手段上，厘清了基本概念、凝练了解题技巧，有助于提升教学效果，但对位移法基本思想的讲授仍未跳出传统范畴，且鲜有涉及课程思政与位移法的有机融合。本文尝试从能量视角，基于“能量平衡”阐述位移法基本思想，重新梳理在荷载及非荷载条件下位移法的解题思路，最后，针对力学课程思政存在的问题，提出以哲学概念为纽带的力学课程思政模式，并以位移法为例展示了课程思政映射与融入的路径和做法。

1 结构力学中的能量原理

万泽青[11]整理和归纳能量原理的知识体系，指出了能量法与静力法的对偶关系，明确了基于最小势能原理的解法本质上是以能量形式表示的位移法。龚相超和胡百鸣[12]探讨了如何完善能量原理的知识体系，如何在力学系列课程中系统地进行优化教学，提出了几门课程间关于加强能量原理教学相关性的几点建议，指出虚功原理的教学是建立能量知识体系的关键。龙驭球[13,14]探讨了结构力学教学的方法论，指出力法和位移法实质是能量法，梳理了结构力学中包括传统形式和能量形式在内的诸多对偶关系，详细探讨了结构力学中的能量原理。前述诸多学者已从理论上论证了能量法与静力法、位移法与最小势能原理的关系，上述观点可作为本文的理论基础和前提，不同之处在于，本文不从数学角度严密论证能量原理之于位移法，而是基于课程教学，以学生为中心，以如何更容易理解、更好熟练掌握位移法为导向，借用“能量原理”着重从物理概念上阐述位移法教学。

2 基于能量视角的位移法教学

在位移法教学中，需要解决三个问题：一是杆端内力与杆端位移（转角、侧移）及荷载之间的函数关系；二是确定结构基本未知量；三是建立求解基本未知量的位移法基本方程。其中尤以推导建立位移法方程是重难点，通常有两种建立方式：一是直接平衡法。不通过基本结构，而借助于杆件的转角位移方程，根据先“拆散”、后“组装”结构的思路，直接由原结构的力偶（独立结点角位移处）或力（独立结点线位移方向）平衡条件建立位移法方程；二是典型方程法。通过选择基本结构，并将原结构与基本体系比较，得出建立位移法方程的平衡条件。典型方程法能以统一的、典型的形式给出位移法方程，其推导方式与力法基本方程的推导方式十分相似，互相呼应，有助于进一步理解位移法基本方程的意义。本文以典型方程法开展基于能量视角的位移法教学。

2.1 基于能量视角的位移法基本思想

下面以具有一个独立结点位移的两个算例说明基于能量视角的位移法基本思想。

如图2(a)所示刚架及图3(a)所示排架，根据结构几何组成分析可知，二者均为有多余约束的几何不变体系，荷载（也包括支座移动、温度变化、制造误差等广义荷载，下同）未作用之前，结构处于稳定状态（假定为稳态一）。静力荷载（指荷载由零逐渐以微小的增量缓慢地增加到最终值，结构在静力加载过程中，荷载与内力始终保持平衡）作用在结构上以后对结构做实功，相当于向稳态一中注入能量，体系最终会归于新的稳定状态（假定为稳态二，也就是结构稳定承载荷载的状态），达到稳态二的充要条件是结构各截面内力（M, FQ, FN）在对应广义位移（d, d,du）上做功，宏观表现为结构发生形变（挠曲和侧移）以便吸收能量，当注入能量与吸收能量相等时，达到稳定状态。

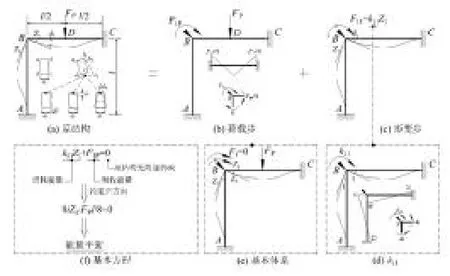
图2 位移法基本思想的图解分析之一——一个独立结点角位移

图3 位移法基本思想的图解分析之二——一个独立结点线位移

观察图2，作用于BC 杆的集中荷载并未与AB杆接触，但仍旧引起了AB 杆的形变及内力，原因在于集中荷载首先引起BC 杆挠曲，进而引起BC 梁B端转动（转角为Z1）。由于B 结点为刚节点，汇交于B 点的杆件变形前后相对夹角不变，因此BC 梁左端转动必然带动AB 杆上端同方向转动（转角同样为Z1），AB 杆上端转动带动整个杆件发生变形。观察图3，均布荷载并未与CD 杆直接接触，但仍旧引起了CD 杆的形变及内力，原因在于均布荷载首先引起AB 杆侧移（侧移为Z1），加之BC 杆轴向变形刚度无穷大，必然导致CD 杆发生同方向侧移（侧移同样为Z1），进而带动整个杆件发生变形。

图2 所示刚架中刚结点B的转角和图3 所示排架中顶端的侧移引起了结构的整体变形，这种具有“纽带、承递”作用的杆端变形称为“核心变形”，在位移法中，亦称作独立结点位移。很显然，“核心变形”带来的结构整体性对于结构受力来说是有利的，从能量角度解释，可视为更多的杆件通过变形吸收能量则各杆件变形较为均匀合理，否则若只有荷载直接作用杆件吸收能量可能会造成变形过大。

在实际情况下，静力荷载施加在结构上会同时伴随结构形变，在本文中，将这一连续、同步过程拆分为荷载施加步（简称“荷载步”）和形变发生步（简称“形变步”）。荷载步只考虑与荷载直接接触杆件在静力荷载逐步增加到指定值的过程中产生的内力（如，图2 中作用于BC 杆的集中力由0 逐渐增加至FP，图3 中作用于AB杆的均布荷载由0 逐渐增加至）；形变步只考虑结构发生宏观的挠曲或侧移。显然，为了实现荷载步和形变步的独立，在荷载步中不考虑结构整体变形，必须人为限制“核心变形”的“纽带、承递”作用。为此，在独立结点位移处增加附加约束（图2b为独立结点角位移，附加约束为刚臂；图3b 为独立结点线位移，附加约束为支座链杆），阻止发生“核心变形”（可将附加约束想象为一只无形的手，这只手握紧结点B让其不再发生转动，或是表现为抵住结点C 让其不再发生侧移）。但在形变步中，必须还原结构的整体变形特性，可令附加约束转动结点（如图2c 所示，转角为Z1）或拉动结构侧移（如图3c所示，侧移为Z1），从而使结构变形与原结构相同。

在位移法中，将在独立结点位移处增加了附加约束的结构称作基本体系（如图2e 及图3e 所示）。为了建立位移法基本方程，将附加约束作为研究对象，并从能量角度寻找平衡方程：在荷载步中，静力荷载引起附加约束中的反力偶（或反力），视为吸收能量（从无到有，隐含被动性。如图2b及图3b中1P）；在形变步中，附加约束主动发生变形（转动或平动），视为消耗能量（从有到无，突出主动性。如图2c 及图3c 中F11）。由于原结构没有附加约束存在，因此针对每一个附加约束，必然要求能量“吸放”相等，即：

上式表征了能量视角下的位移法基本思想，需特别说明的是，“能量”主要有反力偶和反力两种形式，取决于独立结点位移的类型。对于只有1 个独立结点位移的结构，式（2）进一步显示为：

式（3）为位移法基本方程，式中：k11表征在形变步中发生单位形变时附加约束消耗的能量，可由等截面单跨超静定梁在支座位移下弯矩图查询得到（即形常数表，各教材均有集中罗列）；1P表征在荷载步中荷载单独作用时附加约束吸收的能量，可由等截面单跨超静定梁在荷载作用下弯矩图查询得到（即载常数表，各教材均有集中罗列）；Z1表征结构在特定荷载作用下“核心变形”的大小（对于图2 所示刚架为刚节点B 的转角，对于图3 所示排架为结构顶部的水平侧移）。为了便于实现能量的叠加运算，须约定独立结点位移正方向（图2 中约定刚节点顺时针转角为正，图3中约定结构水平向右侧移为正），附加约束反力偶（或反力）正方向与独立结点位移正方向一致。约定正方向后，在查询或记忆形常数表和载常数表时，只需关心弯矩图形状及弯矩值，不需关注弯矩值符号，大大降低了记忆量，减小了计算出错的可能。

由式（3）求解出Z1后，根据弯矩图叠加可求解整个结构的最终弯矩图。

2.2 多个独立结点位移结构

图4 所示结构有两个“核心变形”——刚节点B 处的转角和结构顶端的侧移，即结构独立结点位移数为2，这两个“核心变形”确保了没有和外荷载直接接触的杆件同样可以参与受力，保证了结构的整体性。分别在B 结点和C 结点添加附加刚臂和附加支座链杆，并约定独立结点位移正方向，得到基本结构和基本体系，分别如图4(b)和4(c)所示。如前所述，把荷载作用在结构上引起变形的过程拆分为荷载步、形变步1 和形变步2 三个独立过程。分别以附加刚臂和附加支座链杆为分析对象，确定在上述三个独立过程中能量的吸收和消耗，最终根据式（2）完成基本方程组推导。对于有多个独立结点位移的结构，基本方程推导可借助表1 完成。

表1 基于能量视角的位移法基本方程推导

图4 位移法基本思想的图解分析之三——多个独立结点位移

表1 展示了基于能量视角的位移法基本方程推导流程，根据能量平衡可得到多个独立结点位移状态下位移法基本方程：

根据图5，式（5）中Fip可由载常数表绘制MP图后根据结点力偶平衡和附加支座方向力的平衡计算；k11和k21可由形常数表绘制1图计算得到；k12和k22可由形常数表绘制2图计算得到。

图5 系数和自由项计算

2.3 非荷载因素——支座移动下的位移法

基于能量视角的典型方程法，同样适用于非荷载情况下的超静定结构位移法求解，本文以支座移动为例，如图6 所示两跨连续梁，支座A 发生A转动，支座C 发生△C竖向平动。将支座移动（转动或平动）视为广义荷载，仍旧可以把结构在支座移动下发生形变的连续过程拆分为荷载步（广义荷载单独作用）和形变步（仅独立结点位移处发生变形）两个独立过程。此例以附加刚臂为研究对象，从能量平衡的角度，在荷载步中吸收能量（1p），在形变步中消耗能量，基本方程如式（3）所示。

图6 位移法基本思想的图解分析之四——非荷载因素

3 位移法教学的思政映射与融入

教育部在2020 年5 月颁布的《高等学校课程思政建设指导纲要》中明确指出，“推进课程思政建设是落实立德树人根本任务的战略举措，是全面提高人才培养质量的重要任务”[15]，对于专业教育课程，要求“从课程所涉专业、行业、国家、国际、文化、历史等角度，增加课程的知识性、人文性，提升引领性、时代性和开放性”。对思政元素的挖掘是目前结构力学课程思政的研究热点，传统建筑、大国工程、事故案例、名家事迹、行业标兵、区域特色等素材自然可以服务于课程思政。但结构力学课程思政尚存在专业知识与思政案例“两张皮”以及思政素材囿于力学和结构范畴的问题。

结构力学诸多概念（或方法）之间的伴生关系与哲学中辩证统一的思想相通，因此将力学方法与哲学思想相联系，进而借助高度凝练、概括的哲学思想作为课程思政切入点，实现力学教学与思政案例的“软融入”，能极大拓展思政素材选择范畴，如此，有利于提升专业课程的广度、深度和温度。故此，本文提出“力学知识点→哲学思想→思政素材→思想引导”的课程思政模式，完全可以借助各种案例素材针对性开展价值观教育、传统文化教育、宪法法治教育、劳动与心理健康教育、中华优秀传统文化教育、时政舆论引导等育人工作。根据这一思政模式，基于能量视角，选取“力法与位移法的互补统一、万物相连”“独立结点位移在保证结构受力整体性中体现出的关键少数作用”“结构受力整体性体现的个体和集体关系”“位移法基本方程体现出的平衡思想”等角度作为切入点开展位移法课程思政。本文展示若干位移法课程思政映射与融入设计，如图7 所示。

图7 位移法课程思政映射与融入设计

4 结论

本文针对结构力学求解超静定结构的核心方法——位移法，总结了现有教学存在的不足，阐述了基于能量原理的位移法基本思想，在“能量”及“平衡”思想统领下，介绍了位移法重难点（基本未知量、基本体系、基本结构）的教学思考，进一步通过4 个算例展示了利用“能量”思维的位移法解题思路和步骤。最后，针对现有结构力学课程思政存在“两张皮”和素材选取面狭窄的问题，提出“力学知识点→哲学思想→思政素材→思想引导”的课程思政模式，并以“互补统一”“关键少数”“个体与集体”“平衡思想”等哲学概念为切入点，展示了位移法课程思政映射与融入设计。