IHIE在滚动轴承损伤识别中的应用

孟秋静，杨 钢，王红卫

（1.上海电子信息职业技术学院 中德工程学院，上海 201411； 2.重庆交通大学 机电与车辆工程学院，重庆 400074；3.东南大学 机械工程学院，江苏 南京 210096）

由于长期的高速重载运行，轴承滚珠与内外圈之间易发生磨损，诱发机械设备的共振和损伤［1］。轴承的故障包含了不同损伤类型，也包含不同的损伤程度。因此，建立滚动轴承不同类型和程度的损伤识别模型具有重要意义。

轴承振动是非线性的时间序列，一般采用熵值方法提取其中的非线性信息，如多尺度熵、排列熵等。为从不同尺度表征信号的动态特性，陈鹏等［2］通过多尺度排列熵（multi-scale permutation entropy， MPE）提取轴承的故障信息，实现了轴承损伤的准确检测，但MPE 的粗粒化处理不够精细。为提高分析精度，董治麟等［3］提出了复合多尺度排列熵（complex multi-scale permutation entropy， CMPE），用于轴承的损伤特征提取。随后，Li等［4］在CMPE的基础上，提出了精细复合多尺度排列熵（refine complex multi-scale permutation entropy， RCMPE），可精准识别轴承的损伤类型和损伤程度。然而MPE、CMPE 和RCMPE 这3 种方法的粗粒化处理本质上是一个低通滤波器，其在构建粗粒化序列时仅保留了信号的低频特征，忽略了高频特征［5］。

为提取振动信号的高频特征，Tian 等［6］提出了层次排列熵（hierarchical permutation entropy，HPE），取得了较高的损伤识别精度；然而HPE 随着层数的增加会失去统计可靠性。为此，Li 等［7］利用改进的层次处理缓解了传统层次分析的偏差，提出了改进层次排列熵（improved hierarchical permutation entropy，IHPE），对齿轮箱振动信号进行分析；然而IHPE 会忽略信号的振幅信息，遗漏关键特征。

极限学习机（extreme learning machine，ELM）被广泛用于损伤识别领域。在使用ELM 进行损伤识别前，需要预先给定隐藏层阈值和输入权重，并使用优化算法对两个参数进行自适应优化［8］。

海 鸥 优 化 算 法（seagull optimization algorithm，SOA）具有原理简单、调整参数少等优点，将其用于ELM 的优化，能增强分类器的分类性能和泛化性。例如，孟瑞等［9］使用SOA-ELM 模型对人类的手部动作进行了识别，取得了不错的识别效果。

本文提出了改进层次增长熵（improved hierarchy to increase entropy，IHIE），用于捕捉振动信号的低频和高频信息；再采用SOA-ELM 模型，对IHIE 损伤特征进行损伤分类；最后，采用两组不同损伤类型和损伤程度的滚动轴承数据集，对基于IHIE和SOA-ELM模型的有效性进行检验。

1 改进层次增长熵（IHIE）

IHIE改进了多尺度增长熵（multi-scale increase entropy，MIE）和层次增长熵（hierarchy to increase entropy，HIE）分析不够全面的缺陷，增长熵（increment entropy，IncrEn）的理论参考Wang等［10］的研究。

1.1 IHIE

Jiang 等［11］提出了层次分析方法，可以同时从低频和高频的角度评估信号的动态特性。但是，层次处理会随着层次数k的增加而缩短时间序列的长度。为此，提出了IHIE 方法，该方法利用移动的平均和差分处理代替经典的层次处理，使得层次序列的长度不会随着层次k的增加而缩短。IHIE 的步骤如下：

步骤1对于信号X{x(k)，k=1，2，…，N}，定义平均算子Q0和一个差分算子Q1：

步骤2运算符的矩阵形式(j=0或j=1)在层次数k处可以定义为

步骤3对于k∈N 和唯一向量[r1，r2，…，rk]，整数e定义如下：

式中：{rm，m=1，2，…，k}∈{0，1}为第m层的平均或差分运算符。

步骤4基于向量[r1，r2，…，rk]，可以定义信号的层次分量如下：

步骤5计算各层次分量的增长熵，定义为

1.2 IHIE、HIE和MIE的仿真信号分析

IHIE 的参数包括数据x、嵌入维数m、分辨率参数R和层次数k。Wang 等［10］发现在m=2 和R=4时IncrEn 的分析效果最佳，因此笔者设置m=2 和R=4。对于k，通常设置为k≥3，本文设置k=3。对于数据x，其长度需要进行合理设置。考虑长度N分别为1 024、2 048、3 072、4 096、5 120 和6 144 的白噪声（white Gaussian noise，WGN），计算不同长度WGN的IHIE，如图1所示。

图1 不同长度WGN的IHIE值Fig.1 IHIE values of WGN of different lengths

由图1 可知，当N=1 024 时，熵值曲线互相重合，证明IHIE 对数据长度不敏感。为获得更准确的复杂度测量结果，笔者考虑将N设置为2 048，以避免长度对算法性能的影响。

为了对比IHIE、HIE和MIE的性能，对数据长度N=2 048的WGN进行测试，结果如图2所示。

图2 WGN的IHIE、HIE和MIEFig.2 IHIE， HIE and MIE of WGN

由图2 可知，随着节点的增加，IHIE 出现了较大的跳动，在节点5 处取得最小值，随后曲线上升。而WGN 的复杂性在全频段保持相对一致。因此，MIE 和HIE 都可以较好测量WGN 的复杂性，而IHIE 除了在尺度因子为5时曲线发生跳变，其他节点的熵值也基本保持不变，证明IHIE 也能够较好地测量信号的复杂度。

为量化3 种方法的稳定性，采用IHIE、HIE 和MIE 来分析50 个独立且长度为2 048 的WGN，每种方法的误差见表1。

表1 50组独立WGN的分析误差Tab.1 Analysis error of 50 independent WGN groups

表2 实验1的样本的详细信息Tab.2 Details of the sample in experiment 1

由表1 可知，在大多数节点上，HIE 和MIE 的标准差大于IHIE，这表明IHIE 方法在测量信号的复杂性时具有最好的稳定性。

2 基于海鸥优化算法的极限学习机

极限学习机的隐含层阈值和输入权重对ELM的性能影响较大，为此引入SOA［12-13］来优化ELM，确保了优化的准确性和效率。适应度函数设置为

式中：TF为训练样本的错误识别数量；tF为测试样本的错误识别数量；Tall为训练样本总数；tall为测试样本总数。

SOA优化ELM的具体的步骤如下：

步骤1初始化ELM和SOA的参数，给定海鸥种群的规模、最大迭代次数、变量维度。

步骤2随机产生海鸥种群，各海鸥的位置由隐含层阈值和输入权重进行控制。

步骤3对海鸥的位置进行更新，计算新的适应度，并对比之前的适应度，保存适应度较小的值作为当前最佳解。

步骤4若达到最大的迭代次数，则保存当前获得的最佳适应度，否则返回步骤3。

步骤5根据最优适应度确定海鸥位置参数，即对应ELM的最佳输入权重和隐含层阈值。

3 基于IHIE 和SOA-ELM 的轴承损伤识别

滚动轴承的损伤识别流程为：① 假设滚动轴承有u种损伤类型，每种损伤类型采集50 组样本。② 计算每个样本的IHIE 值，构建表征滚动轴承状态的损伤特征向量。③ 每种损伤类型随机抽取30个样本作为训练样本，剩余20 个样本作为测试样本。④ 给定SOA 的参数（种群大小、最大迭代次数），并对SOA-ELM 模型进行训练。⑤ 基于训练完毕的SOA-ELM 模型，对测试样本进行分类，判断轴承的损伤类型和损伤程度。

4 实验及结果分析

4.1 凯斯西储大学轴承数据验证

振动信号在负载为1 471 W、采样频率12 kHz、电机转速为1 797 r/min的条件下进行采集，采集了滚动轴承的4 种故障状态下的振动信号，分别是健康（标记为NOR）、内圈损伤（标记为IR1、IR2、IR3）、滚动体损伤（标记为B1、B2、B3）、外圈损伤（标记为OR1、OR2、OR3）。不同的编号代表不同的故障严重程度，例如IR1、IR2 和IR3 的损伤程度分别为0.177 8、0.355 6 和0.533 4 mm，上述10种状态的数据的分类编号分别是1～10。利用IHIE 提取10 种状态振动信号的损伤特征，如图3所示。

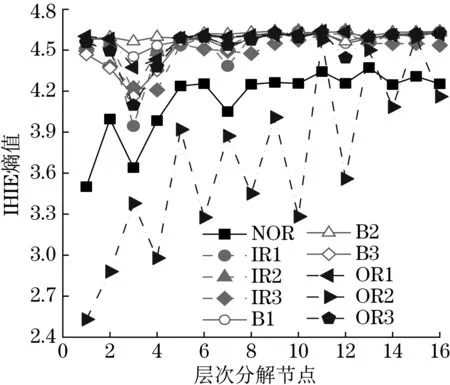
图3 滚动轴承样本的IHIE损伤特征Fig.3 IHIE damage characteristics of rolling bearing samples

由图3 可知，IHIE 能较好地区分轴承的不同损伤状态，特别是NOR 和OR1样本具有显著的差异，证明IHIE 能够表征滚动轴承的不同损伤状态。随后，为了证明IHIE 的有效性和优越性，将由HIE、IHPE、MIE 提取的故障特征输入至SOE-ELM 中进行故障识别，结果如表3所示。

表3 IHIE和IHPE方法的损伤识别结果对比Tab.3 Comparison of damage identification results between IHIE and IHPE methods

由表3可知，HIE、IHDE均取得了100%的识别准确率，证明这两种方法都可以有效识别滚动轴承的不同损伤类型和损伤程度。MPE取得了91.5%的识别准确率。而MIE和HIE方法的识别准确率分别为82%和56.5%，均低于IHIE，证明改进层次处理能够显著提高IncrEn的特征提取性能。

为验证IHIE 的优势，对不同数据长度下基于IHIE 和IHPE 的识别准确率以及特征提取效率进行研究，结果见表3。

由表3 可知，IHPE 在特征提取性能方面要优于IHIE 方法，即使数据长度较短，IHPE 依然能够取得超过98.5%的准确率，证明了其有效性。而IHIE 方法在数据长度大于1 024 后，损伤识别准确率也超过了98%，具有有效性。然而，IHPE 的特征提取效率非常低，特别是在数据长度为512时，其需要441.74 s 进行特征提取，而IHIE 仅需要88.27 s，效率大约是IHPE 的5 倍；在数据长度为2 048 时，IHIE 的效率大约是IHPE 的2 倍。因此，IHIE 不仅具有良好的性能，而且具有较高的效率。

4.2 圣朗戈瓦尔工程技术学院轴承数据验证

为进一步验证本文提出的IHIE-SOA-ELM 损伤识别方法的通用性，利用另一个滚动轴承数据集进行实验，实验平台如图4所示［14］。

图4 滚动轴承实验平台Fig.4 Rolling bearing test platform

在该实验中，转速为2 050 r/min，采样频率为70 kHz，加速度计的型号为PCB 3456A01，采集了轴承座3 个方向的振动信号。试验轴承型号为NU205E。模拟了3 种轴承损伤，分别是内圈、滚动体和外圈，每个损伤类型均包含4 种不同程度的损伤，加上健康状态，共有13 种振动数据。每组样本的长度为2 048个数据点，样本的信息见表4。利用IHIE 方法提取滚动轴承振动信号的损伤特征，如图5所示。

表4 滚动轴承实验样本信息Tab.4 Rolling bearing test platform

图5 滚动轴承样本的IHIE损伤特征Fig.5 IHIE damage characteristics of rolling bearing samples

由表5 可知，在节点为1 时，IHIE 能够区分部分样本，随着节点的增加，区分能力进一步增强，证明了进行层次分析的必要性，但是无法根据熵值来判断样本的损伤状态。

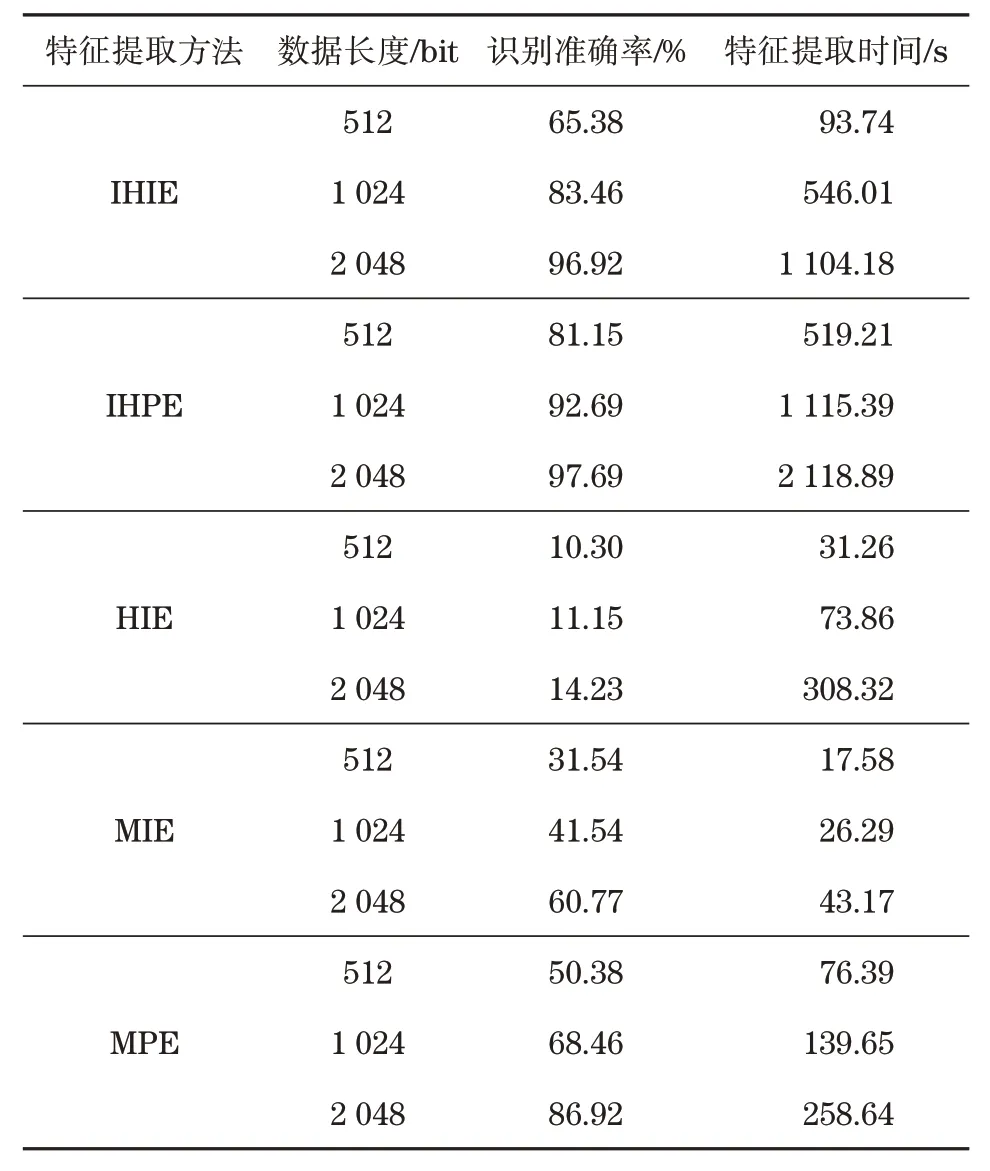
表5 5种方法的损伤识别结果对比Tab.5 Comparison of damage identification results of 5 methods

为了进一步识别滚动轴承的不同损伤状态和损伤程度，利用SOA-ELM 进行特征样本的识别，结果如图5所示。

由表5 可知，IHIE 取得了96.92%的分类准确率，即该方法可以较为有效地识别滚动轴承的故障类型和故障程度。

可以发现，IHIE 虽然准确不是最高的，低于IHPE，但其具有较高的效率。虽然IHPE 的准确率达到了97.69%，但其在特征提取部分所花费的时间几乎是IHIE的2倍，效率非常低。因此，综合来看，所提出的IHIE-SOA-ELM 模型具有较高的效率和准确率，具有一定的优越性。

为进一步验证所提方法的有效性，选择最近5年文献中的相关检测方法进行了对比，见表6。其中，分类器仍然采用SOA-ELM，仅选用文献中的特征提取方法。将提取的故障特征输入至SOA-ELM模型中进行故障识别，并统计特征提取时间。

表6 对比文献的详细信息Tab.6 Comparative literature details

由表6 可知：准确率最高的是文献［10］中提出的RCMPE 方法，达到了95.77%，但特征提取的时间也最长，需要1 338.46 s；特征提取时间最少的为RCMDE 方法，只需要96.09 s，但是准确率仅为76.15%。因此，对比这些方法，所提出的IHIE 方法具有相对优异的性能。

5 结论

针对滚动轴承多个损伤状态和损伤程度下的识别问题，提出了一种结合IHIE 和SOA-ELM 的滚动轴承损伤识别方法。利用两组滚动轴承损伤数据集，对该方法的有效性进行了评估和验证。

（1） IHIE 避免了MIE 无法分析信号高频信息的缺点，同时缓解了HIE 不充分的层次化处理，更适合于提取滚动轴承的损伤特征。

（2） 在两组滚动轴承的损伤识别实验中，IHIE和SOA-ELM分别取得了100%和96.92%的识别准确率，同时特征提取时间分别为848.84 s和1 104.18 s，综合性能最优。