考虑安装误差6σ稳健设计的减速器改进齿面接触分析

徐作栋，董月清，阳小勇

（1.天津职业技术师范大学 机械工程学院，天津 300222； 2.湖南三一工业职业技术学院 智能制造学院，湖南 长沙 410129；3.洛阳有色金属加工设计研究院 技术部，河南 洛阳 471039； 4.湖南大学 机械工程与运载学院，湖南 长沙 410008）

锥齿轮在实际使用中，存在着安装尺寸误差并发生变形的情况［1-2］。锥齿轮在运转时，由于存在一定安装误差，一方面会引起齿轮齿面发生接触性能的变化，导致齿面接触印痕偏离理想条件；另一方面还会形成波动幅度较大的传动误差曲线，使齿轮副传动状态不稳定，出现振动、冲击的情况，齿轮副无法正常运转，使齿轮系统的可靠性下降［3-5］。从当前锥齿轮的加工成本与制造技术水平层面考虑，如要进一步提升齿面平整度与安装精度将会引起成本的明显升高，并不能实现整体经济效益的提升［6］。由此可见，为降低齿轮的安装偏差，促进整体系统稳定性的提升，需要进一步改善啮合特性，这也是优化锥齿轮齿面的重要措施。

Baxter［7］构建了4×2的矩阵用于分析安装误差引起的二阶啮合效果变化，计算时通过差分方法取代求导过程。Litvin 等［8］主要测试了不同错位条件下锥齿轮发生齿面接触整体的变化，同时探讨了安装误差造成的传动误差差异。蔡香伟等［9］通过运用解析计算的方式研究了安装误差引起的齿面啮合性能变化，同时重点分析了敏感度矩阵和V/H 检验的相互影响。根据以上研究结果，吴训成［10］通过显示模式推导得到接触点在公切面中沿垂直方向形成的安装误差敏感度，同时建立了计算公式来实现齿面主动设计。唐进元等［11］分别测试了不同预设点的安装误差灵敏性，重新调整了预定锥齿轮主动设计模式，得到最优预设初始点位置参数，使误差灵敏度系数明显减小；苏进展［12］对差曲面进行全曲率优化调整，从而在安装锥齿轮时获得更优的误差敏感度，通过优化计算确定了可以降低安装误差敏感度的参数，采用量化算法确定了齿面印痕参数，测试了不同安装误差下发生的印痕参数变化规律，针对上述各项参数构建了敏感度矩阵，并利用仿真模型进行了验证，对小轮加工过程的各项参数优化处理得到具有稳定参数的印痕齿面。

本文借鉴前期关于齿轮安装误差与印痕量化的研究成果，在分析安装误差基础上根据印痕特性与6σ稳健优化的方法构建目标函数，通过Monte Carlo 算法完成抽样，采用多岛遗传算法实现二阶接触参数优化并调整安装误差。对比了本文提出的优化方法和确定性优化方法差异性，表明采用本文设计的稳健性方法满足可靠性要求。

1 考虑安装误差的承载接触模型

锥齿轮发生啮合的过程中，齿面在啮入与啮出期间一直保持相切的状态，通过齿轮接触分析（load tooth contact analysis，TCA）实现锥齿轮副接触过程的仿真分析。加入安装误差向量E作为影响因素的条件下采用局部综合法进行分析，对齿面加工参数进行设计优化得到TCA［13］表达式如下：

式中：E为系统的安装误差向量；sp、sg、θp、θg、ϕr1、ϕr2为轮曲面结构参数。

TCA未考虑载荷因素造成的影响，以加载齿轮接触分析（load tooth contact analysis， LTCA）开展分析，得到以下的方程：

式中：F为大小n×n的柔度矩阵；p为载荷矢量；w为间距矢量；Θ为在轮齿弹性变形阶段产生的大轮转角；r1为小轮接触点回转半径矢量；r2为大轮接触点回转半径矢量；d为发生n维变形时得到的间距矢量；T1为小轮输入扭矩。当p≥0，d取值0；当p＜0 时，d取值大于0，d取值为1，2，…，n，n为啮合位置可能发生接触的离散点数量。

LTCA 中包含TCA 算法结果，以式（2）进行计算时，存在安装误差的情况下进行LTCA 计算时，对间距向量与回转半径矢量实施坐标转换，得到安装误差加载齿轮接触分析（installation error load tooth contact analysis，IELTCA）计算式：

2 考虑安装误差的6σ稳健设计

2.1 6σ稳健设计理论

设计产品组成结构及对其进行使用测试时，设计方式与各项影响因素的改变都会反映到产品质量的变化层面，可以将上述变量分成确定性和不确定性2 种类型［14］。齿轮系统安装过程中产生的误差属于不确定变量。6σ稳健优化方法属于一项统计学方法，初始设计阶段可以先建立齿轮安装误差概率模型进行啮合质量分析，根据6σ分析的方法判断各个随机变量引起的啮合性能变化，由此确定符合啮合特性与可靠性的最佳解。按照6σ稳健方法进行优化设计的具体过程是先在某一设计点设置随机扰动信号，再通过算法获得靠近均值点的样本数据，从而评价此方案可靠度与稳健性。以6σ稳健优化方法和确定性优化方法进行差异对比的结果［15-16］如图6 所示。根据如下模型计算式进行稳健优化设计：

式中：X1=［x1，…，xi，…，xn］属于随机变量；y为输出响应；μy、μxi为设计变量；σy、σxi为输出响应方差；xui、xli依次对应随机设计变量xi上限与下限；n为σ水平，在n取值6的情况下，得到6σ稳健模型。

与确定性方法进行比较可知，6σ稳健设计方法可以在远离约束边界条件下得到可靠性优化解。建立目标函数f（x），当随机变量波动幅度为±Δx1时，目标函数形成了±Δf1的大幅波动，位于稳健设计点处；随机变量波动为±Δx2时，目标函数形成了±Δf2的小幅波动，有效抑制稳定性解失效率并减小波动区间，结果如图1所示［16］。

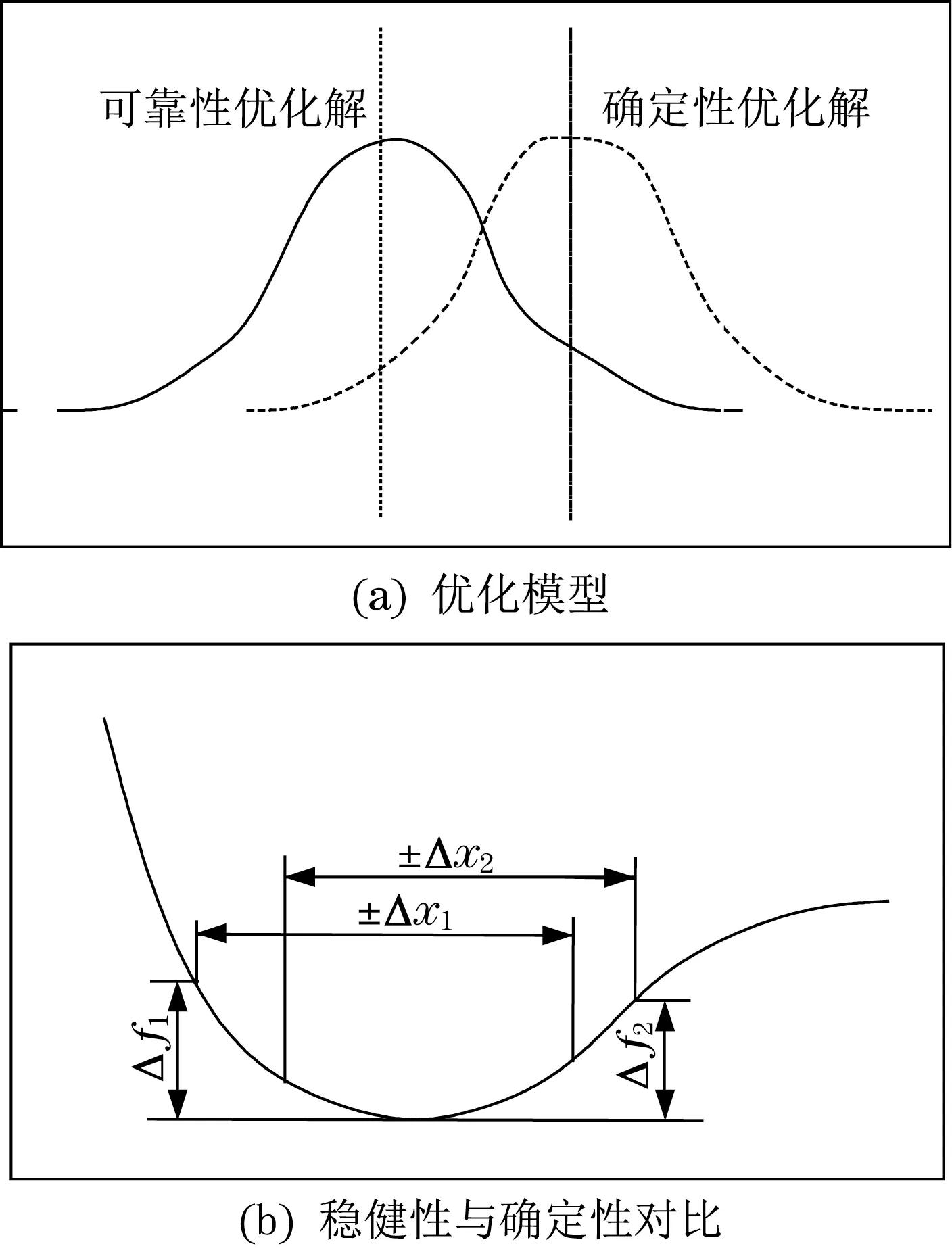
图1 稳健性优化模型Fig.1 Robust optimization model

2.2 基于IELTCA优化设计数学模型

本文以锥齿轮副含安装误差作为依据进行承载接触分析（IELTCA），同时优化了齿面接触印痕中心当量，通过齿面印痕特征当量确定约束表达式，获得下述安装误差齿面6σ稳健优化模型［16］：

式中：η为接触轨迹和齿根之间形成的夹角；m'0为传动比一阶导数；δ为接触区域长半轴与齿宽之比；Hp为小轮轴向位移；Hg为大轮轴向位移；L为大小轮轴线位移；α为大小轮轴线偏角。

目标函数如下：

式中：W1、W2为权重系数；S1、S2为对目标均值和标准差进行归一化的系数；μg、σg分别为印痕中心位置当量值的均值和标准差；E0为期望目标值。

约束条件如下：

式中：S'、d'、e'属于印痕范围、方向与传动精度误差当量；μxi、σxi为xi均值和标准差；xmin、xmax为变量上、下限。

安装误差边界设置见表1，接触边界设置见表2。

表1 安装误差边界设置Tab.1 Installation error boundary setting

表2 接触边界设置Tab.2 Contact boundary settings

由式（5）和式（6）可知，利用6σ稳健优化方法得到的目标函数存在如下2个方面的特征：① 位于印痕中心区域的当量值符合平均性能目标，达到了最低均值。② 发生安装误差波动的情况下，获得与动性能目标相符的输出响应结果，此时达到最低标准差。

根据约束条件考虑印痕常规特征与接触区间形成传动误差变化。采用6σ稳健优化模型进行分析时可以确保方案满足适用性，并在锥齿轮传动阶段获得稳定的安装误差。6σ稳健优化的具体流程［16］如图2所示。

图2 考虑安装误差的6σ稳健优化流程Fig.2 6σ robust optimization flow chart based on installation error

3 算例

本次选择WPLF040型锥齿轮传动过程开展6σ稳健优化处理，齿轮的各项基本参数见表3，初始二阶接触参数见表4。安装误差呈现随机正态分布的特点，以标准差值作为极限值；二阶接触参数都呈现均匀分布的状态，结果见表5 和表6。通过敏感度系数优化确定性，再根据DFSS 分析方法，计算多目标优化的线性加权均值。

表3 齿轮基本参数Tab.3 Basic parameters of round blanks

表4 初始接触参数Tab.4 Initial contact parameters

表5 印痕特征响应结果Tab.5 Results of characteristic response of impressions

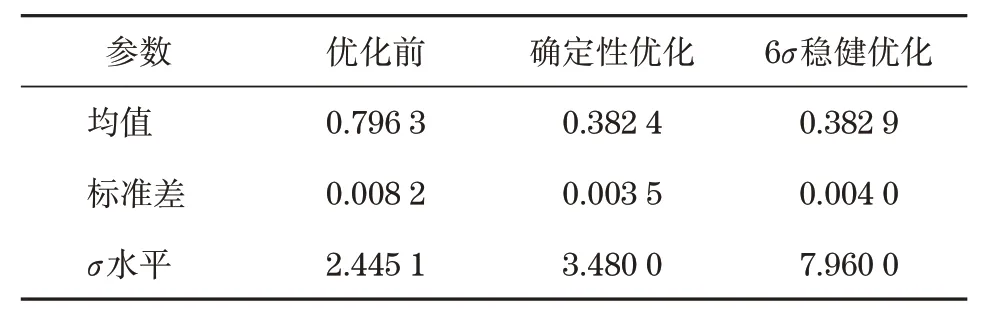
表6 传动误差响应结果Tab.6 Transmission error response results

设定相同的初值，并保持确定性优化结果和稳健优化结果处于同样的安装误差条件下，便于对结果进行比较。按照6σ方法开展分析，对正态随机安装误差进行优化得到二阶接触参数，通过Monte Carlo抽样的方式完成3种结果的100次随机抽样，再对包含安装误差的齿面接触印痕实施IELTCA计算。表5与表6给出了各项参数计算结果。

通过分析3 种方案安装误差随机抽样响应数据可知，没有经过优化的最初参数受到安装误差的影响较大，发生了印痕中心位移的大幅波动，形成了2.43σ的传动误差，未达到稳健性约束的状态，存在失效的问题。通过确定性优化后促进了安装误差稳健性的提升，传动误差为3.52σ，可靠度超过99.9%，此时形成了波动较大的印痕中心，因此并未形成优化边界，存在一定缺陷；6σ稳健优化过程有助于印痕特征形成更稳定的安装误差，传动误差为达到8σ水平，同时可靠度超过99.993 7%，波动区间都未超过优化边界，并实现了印痕中心波动程度的大幅减小，获得了稳定性更高的齿轮系统。

为了比较各方案的控制性能，根据IELTCA 分析接触印痕与传动误差变化曲线。齿轮传动特性对比如图3 所示。由图3 可知，处于不同的二阶接触参数下对应的印痕特征也存在显著差异，显著改善了各安装误差下的传动误差。由于6σ稳健设计传动误差波动相对确定性优化方法减小了30%，由此推断6σ稳健设计具备更优可行性。

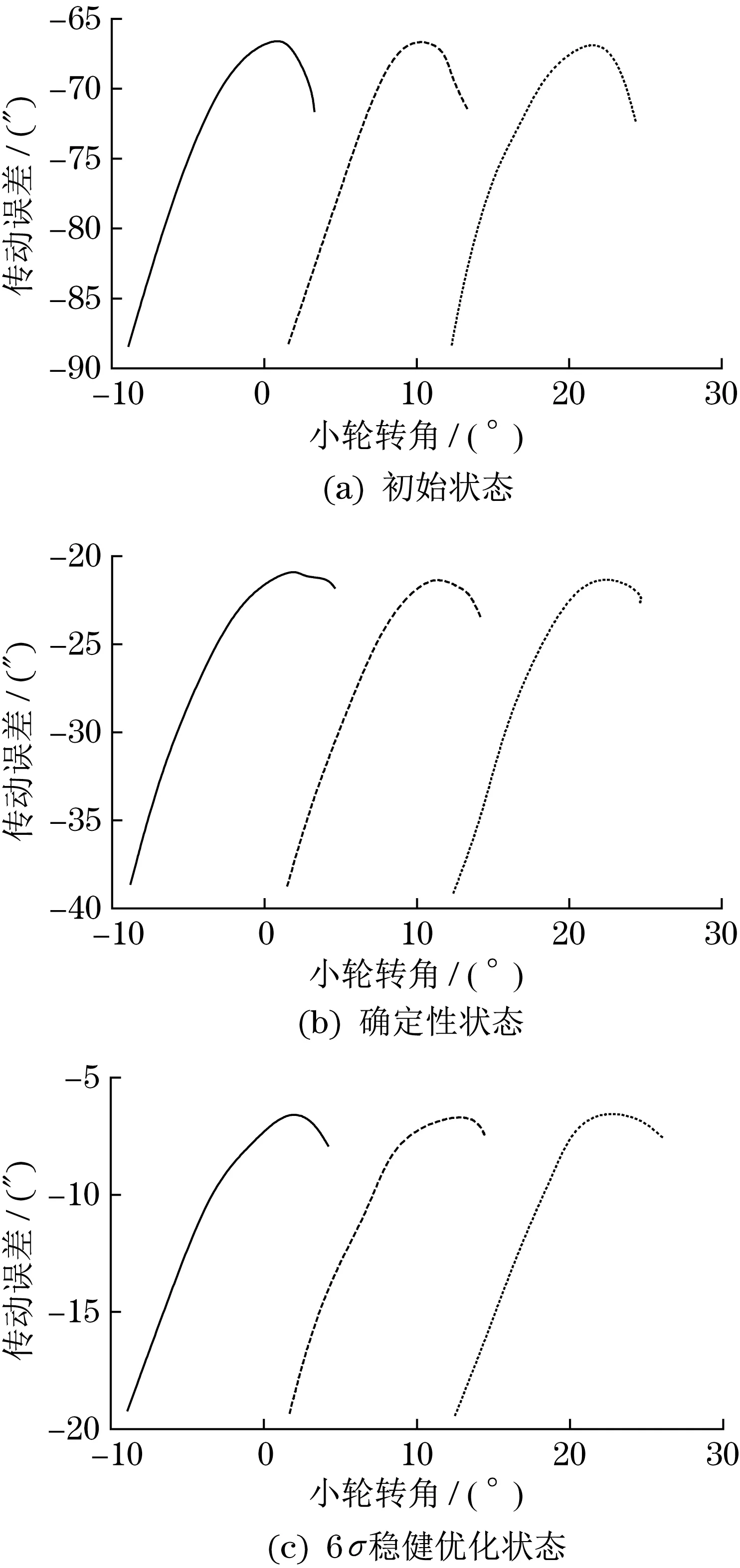
图3 齿轮传动特性对比Fig. 3 Comparison of gear transmission characteristics

5 结论

（1） 6σ稳健优化过程有助于印痕特征形成更稳定的安装误差，可靠度超过99.993 7%，实现了印痕中心波动程度的大幅减小，获得了稳定性更高的齿轮系统。

（2） 处于不同的二阶接触参数下对应的印痕特征也存在显著差异，显著改善了各安装误差下传动误差。6σ稳健设计方法相对确定性优化方法，传动误差波动减小了30%，可行性更好。