复合材料变截面压杆变形性能研究
马 森 赵启林
(1 武警警官学院训练基地,广州 510440)
(2 南京工业大学机械与动力工程学院,南京 211816)
文 摘 为了对复合材料变截面压杆的变形性能进行理论预测,本文以航天器空间桁架结构中的复合材料变截面压杆作为研究对象,首先,基于经典层合板理论,将复合材料变截面杆的壁板等效为主方向与杆轴线方向一致的正交异性板,此时复合材料变截面杆可近似为正交异性杆;其次,基于弹性变形理论和小变形假设,推导了反映杆轴向变形能力的等效轴压刚度理论公式;最后,利用有限元对等效轴压刚度理论的准确性进行了验证。结果表明,不同中间半径和变截面段长度条件下,理论值和有限元值之间的偏差基本保持在3%以内;不同铺层角条件下,理论值和有限元值之间的偏差基本保持在2%以内。因此,本文的理论能够较准确地预测复合材料变截面压杆的变形。
0 引言
空间桁架结构由一定数量的一维杆件在空间拼接而成,非常适用于大型或特大型航天器的构建[1-2]。复合材料因具有诸多性能优势,在卫星承力筒[3]、支架[4]、结构板[5]、支撑杆[6]等场合得到了大量应用。在空间桁架结构中利用复合材料杆作为主承力杆可以充分发挥复合材料的材料优势和桁架的结构优势,在满足结构性能要求的前提下,使得结构的质量更小。
航天器结构上的桁架通常由接头和复合材料杆套接而成,杆通常为变截面杆,变截面杆在实现构件轻量化、提升构件的连接性能等方面较均匀杆件均具有优势,2010 年NASA[6]首次将复合材料变截面杆应用于登月器桁架结构中。前期已有变截面杆结构方面的研究,如王建华[7]推导了在多个横、轴向力协同作用下锥形钢管杆变形的解析计算方法;崔允亮等[8]基于光纤监测技术对大直径变截面钢管复合桩承载性状进行了研究;N.K.GUPTA 等[9]对空心和泡沫填充的复合材料变截面壳进行了轴向荷载作用下的实验研究;H.N.R.WAGNER 等[10]对轴压荷载条件下的复合材料变截面锥形壳进行的屈曲问题的研究;本文作者前期也对复合材料变截面杆进行了研究[11],取得了一定的成果。
基频是在对航天器结构进行设计时需要考虑的重要因素,复合材料桁架结构在满足结构的基频要求方面很有优势[12],在质量确定的情况下,桁架杆的轴向变形性能(或轴压刚度)成为影响桁架结构基频的主要因素。目前,对复合材料变截面杆轴向刚度性能的研究还比较少,本文以航天器桁架结构中的复合材料变截面压杆作为研究对象,从理论角度出发研究杆的轴向变形性能,为复合材料在航天领域的应用提供支撑。
1 复合材料变截面压杆轴向变形问题
复合材料变截面压杆是指截面尺寸沿轴线方向变化的复合材料空心杆,该类杆具有易于实现结构轻量化、便于实现与节点的连接等优点,是航天器桁架结构中常用的主承力构件,如美国Altair 号登月器[6]空间桁架结构主承力构件,如图1所示。

图1 美国Altair号登月器空间桁架结构Fig.1 Aerospace truss structure of America Altair lunar lander
典型复合材料变截面杆的结构和材料相关参数示意图如图2 所示,杆横截面为圆形,沿轴线方向主要分为两个部分:均匀段和变截面段。该类杆与传统杆的区别主要体现在两个方面:材料方面,杆身由复合材料缠绕而成,变形需要考虑复合材料的各向异性;结构方面,杆的横截面尺寸沿轴向是变化的,杆的变形不能再按照均匀杆来考虑。
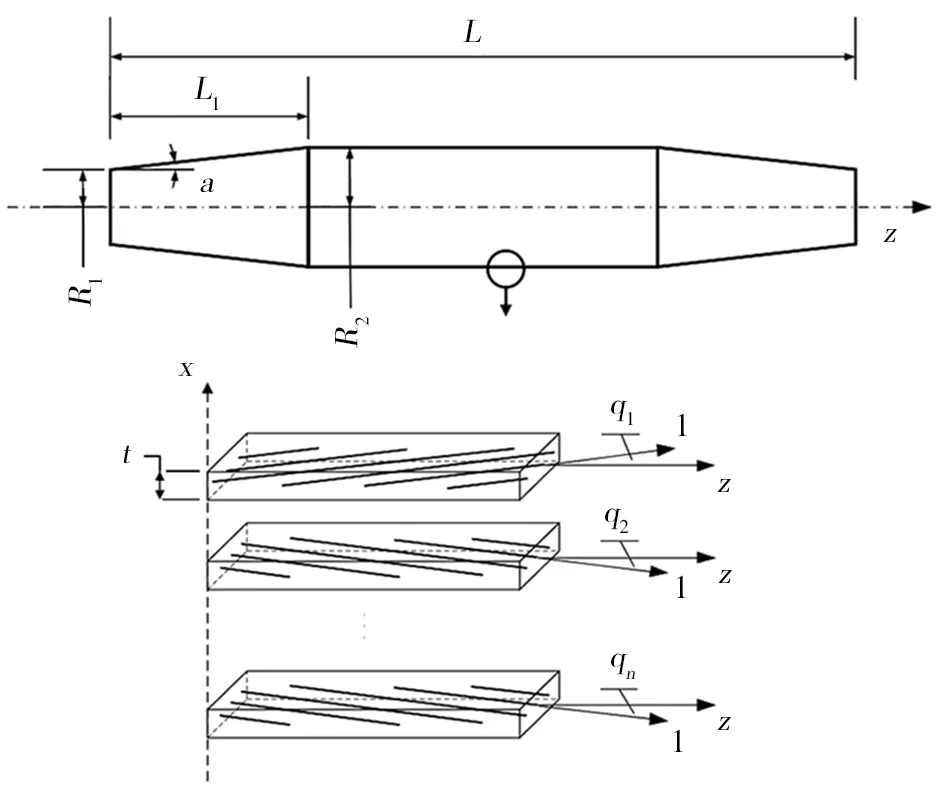
图2 典型复合材料变截面杆结构及材料示意图Fig.2 Diagram of structure and material of composite strut with varying cross-section
对于图2中的复合材料变截面杆,截面变化可以通过截面半径沿轴线方向的变化方程表示:
式中,半锥角α表示变截面段回转体母线与杆轴线方向的夹角,小变形情况下可以认为截面半径的方程保持不变。
作为航天器空间桁架结构的主承力构件,复合材料变截面杆的轴向变形性能(轴向刚度)对结构的基频产生重要影响,因此对复合材料变截面杆的轴向变形性能进行分析十分重要。
2 基本方法
本文采取的基本思路是:首先基于经典层合板理论,将空心杆壁板的平衡-对称复合材料层合板等效为主方向与杆轴线方向一致的正交异性单层板(图3),求得该正交异性单层板主方向的弹性参数;然后基于小变形假设,根据轴向荷载F和结构特点求得沿轴线方向的变形ΔL,继而根据式(2)求得杆的等效轴压刚度[EA]。

图3 平衡-对称复合材料层合板的近似Fig.3 Approximation of balanced-symmetric composite laminates
[EA]反映了复合材料变截面杆在轴力作用下的轴向变形能力,[EA]越大,杆件的轴向变形能力越小,[EA]越小,杆件的轴向变形能力越大。
2.1 刚度等效参数
对于复合材料层合板,以单位尺寸的壳体微元作为研究对象,该微元体上的内力分别为Nx、Ny、Nxy,根据复合材料力学[13-14],层合板内力和应变之间的关系可以写为:
式中,aij(i,j=1,2,6)为六阶柔量矩阵a中对应位置的元素,称为柔量系数,柔量系数是和材料参数、层数、铺层厚度、铺层角度有关的量。对于平衡-对称铺层,忽略平面内、外的应力耦合效应,在单向荷载Nx(Ny=Nxy=0)的作用下
可得x方向的弹性模量
式中,h为层合板的厚度。同理可得y方向的弹性模量
2.2 轴向变形计算公式
变截面杆的母线可以看作在A 点出现折点的折线(图4),其中区域①对应杆的变截面段、区域②对应杆的均匀段。
轴向荷载F的作用下,由于环向约束等作用(实际应用中,在折点A 处一般也会做加强处理),可以假定杆件在折点A 处承受图4所示的“滑轮约束”,即在外界荷载F的作用下,A 点两侧所承受力的大小是相等的,亦即
此时,A点两侧回转体母线方向的面力均为:
式中,Rz为任意一点z处的截面半径。
对图4 中复合材料变截面杆轴向变形的分析可以针对变截面段和均匀段分别考虑。
2.2.1 变截面段轴向变形的分析
如图5所示,取左侧变截面段作为研究对象。

图5 变截面段结构Fig.5 Structure of the part with varying cross-section
母线为直线,由空间几何关系可得母线的长度
截面上任意一点z处的半径Rz可以根据公式(1)求得,则z处单位圆周上母线方向的面力为
式中,h为杆壁板的厚度。
平均应变为
式中,Ez为杆壁板沿母线方向的弹性模量,可以根据式(5)求得。
将平均应变Δε沿母线方向积分可得母线方向的变形量:
根据空间几何关系可得沿杆轴线方向的长度变化量为:
2.2.2 均匀段轴向变形的分析
均匀段长度L2=L-2L1,半径为R2,轴力F作用下,均匀段轴向变形为:
荷载p作用下的轴向变形量为变截面段和均匀段变形之和:
根据杆的长度和变形可以求得杆的等效轴压刚度[EA]:
从式(18)可以看出,影响复合材料变截面杆轴向变形性能的参数既有材料层面的参数Ez,也有结构层面的参数L1、R1、R2等。
下面利用有限元对该公式的准确性进行验证。
3 数值算例
本节利用有限元对推导的复合材料变截面杆等效轴压刚度理论进行验证。
3.1 算例描述
算例中用到的材料为IM7/5582 复合材料铺层,材料属性如下:E1=144.79 GPa,E2=E37.58 GPa,G12=G213.6 GPa,μ12=μ21=0.3,μ23=0.35。单个铺层的厚度标记为t。
利用有限元分析软件ANSYS对复合材料变截面进行参数化建模和变形计算,典型有限元模型如图6所示。

图6 复合材料变截面杆典型有限元模型Fig.6 Typical finite element model of composite strut with varying cross-section
ANSYS 中,在复合材料变截面压杆一端施加轴向压力F,并计算其轴向变形量ΔL,根据式(2)即可求得其等效轴压刚度[EA]。
3.2 结果及分析
分别改变变截面杆中间半径R2、变截面段长度L2和复合材料铺层角θ的值,分析这些参数的改变对等效轴压刚度[EA]理论准确性的影响。
3.2.1 中间半径R2的影响
控制IM7/5582 复合材料铺层的厚度为t=0.1 mm、铺层序列[75,-75,-65,65,65,-65,-75,75](与环向的夹角)、杆长L=1 600 mm、变截面段的长度L1=400 mm、固定端半径R1=20 mm、轴向荷载p=128 kN。取R2为区间[25,100] mm中的一系列值。
图7 给出了理论和有限元计算结果随R2的变化趋势;图8给出了理论值和有限元值之间的偏差随R2变化的趋势。

图7 R2对等效轴压刚度的影响规律Fig.7 Influence of R2 on the equivalent axial compression stiffness

图8 理论值和有限元值之间的偏差随R2变化的趋势Fig.8 Deviation between theoretical value and finite element value along with the change of R2
从图7 可以看出,随着R2的增大,等效轴压刚度[EA]随之增大,这是因为R2增大后,杆的横截面面积增大,在弹性模量保持不变的情况下,杆的等效轴压刚度基本与横截面面积成正比,此时杆的等效轴压刚度肯定增大。
从图8 可以看出,随着R2的增大,理论值和有限元值之间的偏差基本保持在3%以内。
3.2.2 变截面段长度L1的影响
控制杆总长为L=1 600 mm、固定端半径R1=20 mm、中间半径R2=60 mm、铺层序列[75,-75,-65,65,65,-65,-75,75](与环向的夹角)、轴向荷载p=128 kN。取L1为区间[100,750] mm 中的一系列值,得到的计算结果如图9所示,理论值和有限元值之间的偏差如图10所示。

图9 L1对等效轴压刚度的影响趋势Fig.9 Influence of L1 on the equivalent axial compression stiffness
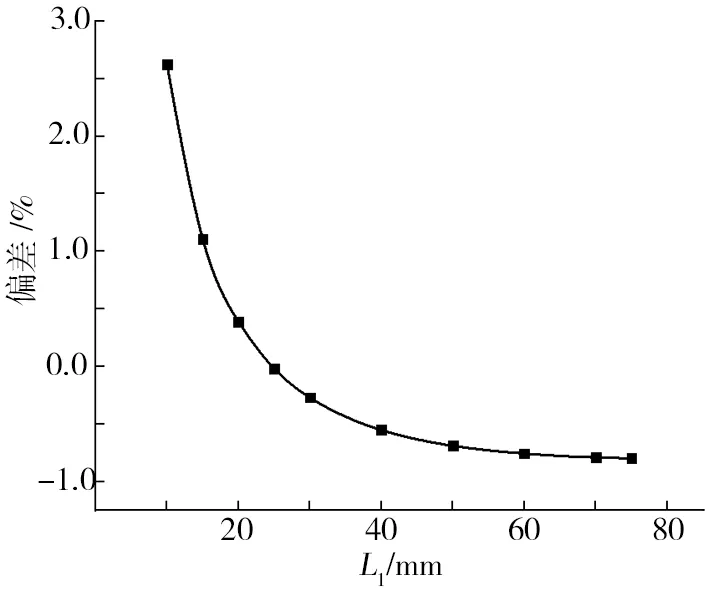
图10 理论值和有限元值之间的偏差随L1变化的趋势Fig.10 Deviation between theoretical value and finite element value along with the change of L1
从图9 可以看出,在其他参数固定的情况下,随着L1的增加,等效轴压刚度[EA]随之减小,这是因为随着L1的增大,相同位置处,杆件的横截面面积变小,轴向应力增大,轴向变形增大,加大了杆件的轴向变形,等效轴压刚度变小。
从图10可以看出,随着L1的增加,理论值和有限元值之间的偏差基本保持在3%以内。
3.2.3 铺层角的影响
控制杆总长为L=1 600 mm、固定端半径R1=20 mm、中间半径R2=60 mm、变截面段长度L1=400 mm、轴向荷载p=128 kN。铺层序列为[θ]bs形式,“[θ]bs”表示铺层按照平衡-对称方式排列,铺层角θ取区间[0,90]中的一系列值,得到的计算结果如图11所示,理论值和有限元值之间的偏差如图12所示。
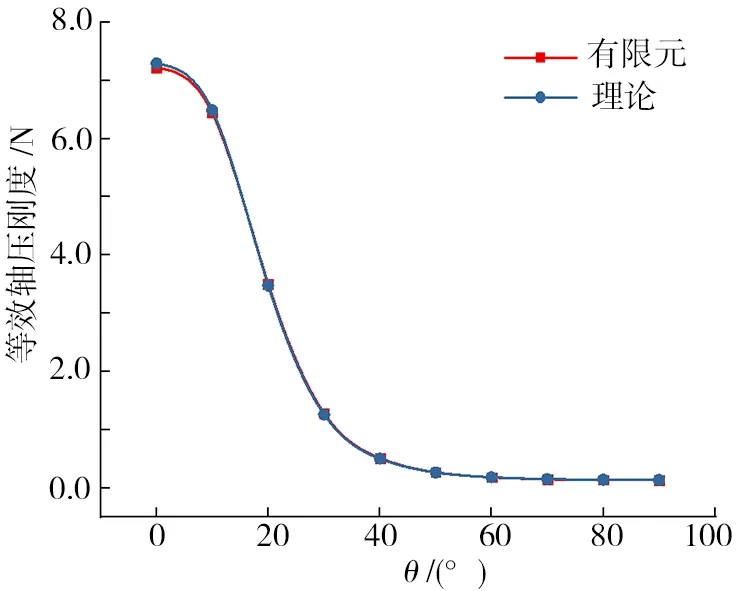
图11 铺层角对等效轴压刚度的影响趋势Fig.11 Influence of ply angle θ on the equivalent axial compression stiffness

图12 理论值和有限元值之间的偏差随铺层角θ变化的趋势Fig.12 Deviation between theoretical value and FE value along with the change of ply angle θ
从图11可以看出,在其他参数固定的情况下,随着铺层角的增加,等效轴压刚度随之减小,这是因为随着铺层角的增大,杆件壁板的铺层在轴线方向的等效弹性模量Ez减小,相同荷载时杆的变形增大,等效轴压刚度减小。
从图12可以看出,随着铺层角的变化,理论计算值和有限元计算值之间的偏差基本保持在2%以内。
3.3 讨论
本节分析了复合材料变截面杆中间半径、变截面段长度和铺层角的变化对等效轴压刚度的影响。结构层面,考察了中间半径和变截面段长度对等效轴压刚度理论准确性的影响,理论值和有限元值之间的偏差基本保持在3%以内。材料层面,考察了铺层角对理论值准确性的影响,理论值和有限元值之间的偏差基本保持在2%以内。
本节的工作表明,提出的理论能够较好地预测复合材料变截面杆的轴向变形性能。
4 结论
本文的工作拓展了复合材料结构计算理论的研究,研究结果对实际工程中的复合材料结构设计具有指导意义,为进一步工作奠定了基础,具体研究过程中得到以下结论。
(1)分析复合材料变截面压杆的轴向变形性能,在材料层面需要考虑复合材料铺层力学性能的影响,在结构层面需要考虑截面变化的影响。
(2)复合材料变截面杆的壁板由多个铺层角度不同的复合材料缠绕而成,利用等效参数的思想将复合材料空心杆的壁板等效为主方向与杆轴线方向一致的正交异性板,此时复合材料杆可以近似为正交异性杆,同时可以得到正交异形板主方向的材料弹性参数;
(3)针对得到的正交异性杆,基于小变形假设,推导了反映杆轴向变形能力的等效轴压刚度计算公式,该公式可以同时考虑材料参数和结构参数;
(4)利用有限元对推导的等效轴压刚度理论的准确性进行验证和讨论,结果表明,本文的理论能够较准确地预测复合材料变截面杆的轴向变形性能。

