斜纹机织热塑性复合材料低速冲击损伤及多尺度数值模拟研究

章韫杰 高飒飒 王泽雨

（陕西科技大学机电工程学院，西安 710021）

文 摘 机织复合材料在服役过程中不可避免地遭受低速冲击而引起内部损伤，导致材料性能减退。本文以斜纹机织热塑性复合材料为研究对象，通过实验与模拟相结合的方法研究其在低速冲击下的损伤行为。构建了微观、介观和宏观串行的多尺度模型对斜纹机织热塑性复合材料低速冲击损伤行为进行预测，并在5和10 J的冲击能量下，对其进行低速冲击试验以验证该多尺度模型的正确性。结果表明，微观、介观和宏观串行的多尺度模型能够准确地预测出斜纹机织热塑性复合材料的冲击损伤特性；在较大的冲击能量下，材料正面和背面均出现了损伤，且损伤以纤维断裂为主；低速冲击数值模拟所预测的力响应曲线与试验结果表现出良好的一致性，数值模拟损伤面积的误差在10%以内。

0 引言

机织热塑性复合材料具有良好的力学和成型性能，广泛应用于各种结构件［1］。而航空复合材料结构件，在实际服役中会受到砂石、冰雹等物体的低速冲击，从而引起材料的损伤。在后续受力情况下，由冲击引起的损伤会逐步扩展，造成材料力学性能的衰退，进而引起结构件失效，形成重大安全隐患。因此，开展机织热塑性复合材料低速冲击损伤的研究十分必要，可为复合材料结构件的服役提供安全保障。

国内外学者对纤维增强树脂基复合材料的低速冲击损伤进行了大量的研究，包括不同温度、湿度等环境下的材料老化［2］，冲击角度、冲击物的形状和材质［3］以及材料自身结构［4］对其抗冲击性能的影响。但以上研究工作大多数是针对单向热固性复合材料层合板，只有少部分是关于机织热塑性复合材料，且主要集中在研究环境温度［5］和树脂力学性能［6］对其冲击损伤特性的影响。由于冲击试验的成本和时间周期较高，部分研究者对机织复合材料冲击损伤进行了数值模拟研究［7-8］。然而，多数研究只在机织复合材料的宏观层面展开，而机织热塑性复合材料的多尺度特性，决定了其力学性能不仅依赖于其构成材料（基体和增强体）的力学性能，同时也依赖于材料的微观结构。

在多尺度建模方面，已有的研究工作大多是对热固性复合材料进行多尺度建模，并预测其力学性能和损伤行为［9-10］。惠新育等［9］基于能量法在微观和介观尺度下对平纹编织SIC/SIC 复合材料层合板的弹性常数进行了预测，引入Tsai-Wu 准则及最大应力准则，在介观尺度下对材料的纵向拉伸强度进行了预测。MA 等［10］在微观尺度中采用平均场法预测具有纳米填料基体的弹性模量，将该弹性模量输入介观模型预测整体力学性能，然后，将该力学性能输入到宏观模型中进行低速冲击模拟。上述研究虽然考虑了材料的多尺度特性，但其在数值模拟中将基体和纱线视为弹性体，未考虑塑性变形。

针对这一问题，SUN 等人［11］利用多尺度建模的方法开发了碳纤维增强聚合物复合材料的模型框架，提出了单向复合材料的弹塑性损伤本构模型，通过介观尺度的代表性体积单元（RVE）分析了机织物和片状模塑复合材料的失效机制。ZHOU 等［12］分别为纱线、基体和界面层建立了具有塑性、拉压不对称性的损伤本构模型，以预测材料的损伤。上述研究虽然考虑了机织复合材料的塑性变形，但仅在微观和介观尺度上考虑材料的内部损伤，并未研究微观和介观尺度上的损伤对材料宏观力学性能的影响。

本文采用试验和数值模拟相结合的方法，研究斜纹机织热塑性复合材料在低速冲击下的损伤行为。首先，根据斜纹机织热塑性复合材料的多尺度模型框架（图1）建立了多尺度模型，其考虑了微观尺度的基体塑性变形以及介观尺度的基体和纱线（本文的纱线是指浸入基体的纤维束）塑性变形，以实现微观-介观-宏观之间的参数传递。其次，通过微观RVE 模型预测纱线的力学性能，然后将其传递到介观RVE 模型预测宏观机织热塑性复合材料的力学性能。最后，在宏观尺度上进行低速冲击模拟，并与试验结果进行对比以验证模型的有效性。本文对促进机织热塑性复合材料在各类工程中的应用具有重要的意义。

图1 多尺度模型框架Fig.1 Multi-scale model framework

1 材料及试验准备

1.1 材料制备

1.1.1 原材料

本研究的原材料为斜纹机织热塑性复合材料预浸料，碳纤维为T300/3K，其力学性能参数如表1 所示（由上海邦麟复合材料科技有限公司提供）。基体为尼龙6（PA6），型号为YH-800，其力学性能通过试验测定。

表1 T300/3K碳纤维的力学性能参数1）Tab.1 Mechanical properties of T300/3K carbon fiber

1.1.2 机织热塑性复合材料试样的制备

机织热塑性复合材料由8层预浸料压制而成，将150 mm×100 mm 的预浸料堆叠放置于表面均匀涂抹聚氨酯脱模剂的模具中，温度达240℃时，将模具置于平板硫化机中（ZS-407DP-30-400），如图2 所示。进行预热，预热时长为10 min，然后在0.1 MPa 压力下预压4 min 后，将压力增至1 MPa，保温保压20 min，待冷却至室温后进行脱模。固化完成后，利用磨抛机去除毛刺与飞边，最终制备的机织热塑性复合材料样本尺寸为150 mm×100 mm×2.72 mm。

图2 层合板成型过程Fig.2 Laminate forming process

1.2 试验准备

1.2.1 树脂基体的力学性能测定

拉伸试验和压缩试验是在万能试验机（ETM104 B）上进行的，拉伸试样和压缩试样通过注塑机（TT1-130F2V）注塑成型。在成型前，树脂颗粒需要在110℃的真空下干燥10 h。

树脂基体的拉伸测试依据ASTM D638 标准，设定万能试验机的拉伸速率为5 mm/min，利用DIC（VIC-3D）追踪其应变变化，测得弹性泊松比和塑性泊松比。压缩测试参照ASTM D695 标准，以1 mm/min 的压缩速率测得压缩应力应变曲线，获取压缩强度。最终得到树脂基体PA6 的力学性能参数，如表2所示。

表2 树脂基体PA6的力学性能参数Tab.2 Mechanical properties of PA6 resin matrix

1.2.2 低速冲击试验

根据ASTM D7136 标准，使用Instron Dynatup 9250HV 落锤冲击试验装置（图3）对1.1.2 所制备的机织热塑性复合材料试样进行低速冲击试验，冲头质量为5.607 kg。试样放置在图3 所示的矩形夹具中，下方有一个125 mm×75 mm矩形开口，4个橡胶头夹住试样防止其向平面外移动。冲击能量的大小由冲头初始高度控制，试验需进行两组（冲击能量为5和10 J），每组至少进行3次以保证结果的重复性。

图3 落锤冲击试验装置Fig.3 Drop weight impact test device

2 机织热塑性复合材料多尺度模型

2.1 多尺度有限元几何模型

根据图1 的多尺度模型框架，分别构建了微观、介观和宏观的有限元模型，以实现微观-介观-宏观之间的参数传递。

2.1.1 微观尺度RVE模型

微观尺度的RVE 定义了碳纤维嵌入基体的周期性阵列结构，如图4所示。RVE的几何尺寸大小为单位值，即长度和宽度为L=W=1，高度H=纤维体积分数为κ=0.6（由上海邦麟复合材料科技有限公司提供）。纤维和基体的力学性能参数分别如表1和表2所示，用于后续机织热塑性复合材料力学性能的计算模拟。

2.1.2 介观尺度RVE模型

机织热塑性复合材料介观尺度RVE 模型主要由基体和机织物组成［图5（a）］，机织物由经纱和纬纱交替机织组成，且两种纱线的力学性能相同。机织物的横截面［图5（b）］几何参数见表3。根据其几何参数在三维软件中绘制出介观RVE 的几何模型，所建立的RVE 几何模型的长和宽均为6.8 mm，厚度为0.34 mm。

表3 机织物横截面的几何参数Tab.3 Geometric parameters of woven fabric cross-section

图5 介观尺度RVE Fig.5 Meso-scale RVE

2.1.3 宏观低速冲击模型

宏观尺度有限元模型包括机织热塑性复合材料、支撑板和冲头，其尺寸均与试验一致。冲头的质量亦与试验一致，其在Abaqus中通过材料属性定义。冲头与试样之间采用一般接触算法，摩擦因数为0.3。试样和支撑板之间采用绑定约束，并对支撑板的底面施加固定约束。每层试样的单元类型为C3D8R，层与层之间插入零厚度的内聚力单元（COH3D8）以模拟层间界面。为了保持层间应力的连续性，内聚力单元与其上下相邻单元共节点。所建立的宏观低速冲击模型如图6所示。

图6 宏观低速冲击模型Fig.6 Macro-scale low-velocity impact model

2.2 周期性边界条件

在介观尺度和微尺度的数值模拟中，必须对RVE 施加周期性边界条件以保证位移边界连续性。LI［14］提出RVE 平行边界表面上的每一对节点的位移为：

上式的关系可以通过设置平行边界表面上每对节点之间的位移线性约束来实现。

2.3 损伤模型

图7为材料损伤模型框架。在该模型中，为碳纤维和宏观机织热塑性复合材料建立弹性损伤模型，为热塑性基体和介观尺度的纱线建立弹塑性损伤模型。并将上述损伤模型通过Abaqus 软件的VUMAT用户子程序嵌入执行。

图7 材料损伤模型框架Fig.7 Material damage model framework

2.3.1 碳纤维的弹性损伤模型

碳纤维由于其长径比较大，表现出横观各向同性的特点，采用最大应力准则来表征纤维的损伤起始［15］：

式中，Xft和Xfc分别为纤维的拉伸和压缩强度，σi为纤维的应力，i=1，2，3。

本文采用基于断裂韧性的损伤退化准则来描述纤维的损伤演化，并引入特征长度Lc来定义失效应变，以减轻网格依赖性。

对于纤维来说，拉压载荷下等效初始应变及最终失效应变的表达式分别如下：

式中，Ef11为纤维纵向方向模量，Gft和Gfc分别为纤维的拉伸及压缩断裂韧性。

损伤演化如下：

式中，εf为纤维纵向的应变分量。为损伤变量，当其达到1时，单元完全失效并删除。纤维连续损伤模型详细定义参考文献［15］。

2.3.2 基体的弹塑性损伤模型

基体可视为各向同性的弹塑性固体，遵循Melro等人提出的各向同性损伤定律［16］，采用了抛物面屈服准则：

式中，Xmt和Xmc分别是拉伸和压缩强度。J2是偏应力张量的第二不变量，I1是应力张量的第一不变量，其表达式为：

式中，σ11、σ22和σ33为基体的应力。

基体损伤起始为［16］：

损伤阈值rm可定义为：

基体采用指数型损伤演化，其表达式为

式中，Am为基体退化定律参数，基体连续损伤模型详细定义参考文献［16］。

2.3.3 纱线的弹塑性损伤模型

纱线在不同方向的拉伸和压缩上均表现出各向异性的力学行为，因此纱线的弹塑性行为由Liu-Huang-Stout 屈服准则［12］描述。屈服准则的定义如下：

式中，F、G、H、I、J、K、M、N为当前各向异性的特征参数。1 方向（纵向）沿纤维方向，2 方向（横向）垂直纤维方向。F、G、H、I、J、K、M、N的定义如下：

式中，Xwt和Xwc表示纵向拉伸和压缩强度，Ywt和Ywc表示横向拉伸和压缩强度，Sw12是面内剪切强度，Sw13是面外剪切强度。

为了捕捉不同方向的失效模式，采用改进的Chang-Chang 失效准则［12］判断其损伤起始，损伤起始如下：

式中，rI为损伤阈值，为负载函数：

纵向拉伸（σ11＞0）：

损伤演化为指数型损伤演化：

式中，AI为定义纱线退化定律参数，纱线连续损伤模型详细定义参考文献［17］。

2.3.4 机织热塑性复合材料的弹性损伤模型

机织热塑性复合材料可视为弹性体，其每一层可以看作正交异性材料。因此采用6 种损伤变量描述其损伤起始［18］：

经向拉伸（σ11＞0）：

经向压缩（σ11＜0）：

式中，Xht和Xhc分别为经向的拉伸和压缩强度，Yht和Yhc分别为纬向拉伸和压缩强度，Zhc为面外压缩强度，Sh13和Sh23是面外剪切强度，Sh12是面内剪切强度。

应力加载过程中，一旦达到失效标准（Ri≥1），即进行损伤演化，其定义为：

式中，mi为材料退化定律参数，i为相应的损伤模式，机织热塑性复合材料连续损伤模型的详细定义参考文献［18］。

2.4 内聚力模型

材料层与层之间通过插入内聚力单元来模拟其分层损伤。损伤的发生由二次名义应力准则［19］判定，该准则为：

式中，tn、ts和tt表示界面单元的法向正应力和面内剪切应力代表界面单元的法向强度和面内剪切强度。

损伤发生后，利用Benzeggagh-Kenane 定律［19］描述界面的损伤演变：

表4 层间内聚力单元力学性能参数Tab.4 Mechanical properties of inter-layer cohesive element

3 结果讨论和分析

3.1 机织热塑性复合材料力学性能参数预测

采用2.1.1 所建立的微观RVE 模型预测纱线的力学性能，分别对施加了周期性边界条件的微观RVE 模型进行纵向拉伸和压缩、横向拉伸和压缩、面内剪切和面外剪切的虚拟加载试验。图8 为不同边界条件下微观RVE 应力应变曲线图，在纵向拉伸和纵向压缩时，碳纤维为主要受力对象，故强度最高，拉伸模量和压缩模量相同；在横向拉伸、横向压缩和面内剪切时，应力应变曲线呈非线性，因为此时纱线的强度主要由基体决定。最终纱线的力学性能参数如表5所示。

表5 纱线的力学性能参数Tab.5 Mechanical properties of yarns

图8 不同边界条件下微观RVE应力应变曲线图Fig.8 Micro-RVE stress-strain curves under different boundary conditions

将基体和纱线的材料参数输入到介观尺度模型中，由于斜纹机织热塑性复合材料具有横观各向同性的特征，对2.1.2 所建立的介观RVE 模型施加周期性边界后，进行纵向拉伸和压缩、法向拉伸和压缩、面内剪切和面外剪切的虚拟加载试验，得到单层试样的力学性能参数。依据文献［20］的结论，机织物层合板的强度与层数成正比，得知冲击试样（8层）的强度为单层试样强度的8 倍。表6 给出了斜纹机织热塑性复合材料的力学性能参数。

表6 斜纹机织热塑性复合材料的力学性能参数Tab.6 Mechanical properties of twill woven fabric reinforced thermoplastic composites

3.2 机织热塑性复合材料冲击损伤分析

3.2.1 冲击力分析

将5 和10 J 冲击能量的冲击试验与数值模拟的结果进行对比。由图9（a）冲击力-时间曲线可见，相同冲击能量下，仿真和试验曲线一致性良好。在冲击能量为5 J 时的曲线呈正弦形，加载和卸载部分是平滑的，但在达到最大冲击力之前，曲线出现了轻微的振荡，主要原因是在冲击力上升阶段材料已经产生了一定的损伤。同样的，在冲击能量为10 J 时，在达到最大冲击力之前材料已经产生了损伤，曲线出现了轻微的振荡，当冲击力达到最大时，材料损伤加剧，出现了剧烈的振荡，导致冲击力突然下降。

图9 冲击力在不同能量下试验和仿真对比图Fig.9 Comparison of test and simulation of impact force under different energies

图9（b）冲击力-位移曲线对比图，仿真和试验的曲线趋势一致。两种冲击能量下的曲线均呈现出3个阶段：第一阶段为冲头向下冲击试样，此时冲击力随着位移增加而增大，冲击力与位移为线性关系。第二阶段为振荡阶段，此时冲击力和位移均已接近最大值。第三阶段是冲头回弹阶段，试样弹性势能转化为冲头的动能使冲头发生回弹，整个回弹过程呈非线性。冲击能量为5 J 的曲线较为平滑的，而冲击能量为10 J的曲线较为振荡。

3.2.2 吸收能量分析

图10为两种冲击能量下仿真和试验所得的吸收能量-时间曲线对比图，相同冲击能量下仿真和试验的曲线趋势一致。试样在两种冲击能量下的吸收能量-时间曲线可分为3 个阶段：第一阶段吸收能量快速增加，其曲线的斜率也在逐渐增大，该阶段对应冲击力-时间曲线中的冲击力上升阶段，此时试样出现损伤，冲头的动能被吸收；第二阶段吸收能量增长的趋势变缓并达到最大值，此阶段对应于冲击力-时间曲线的振荡阶段，也标志着冲头从向下冲击变成向上回弹；第三阶段吸收能量下降，此阶段全程为冲头的回弹过程，由于弹性势能作用于冲头，因此试样吸收的能量逐渐减少，使得其能量最终稳定下来，此时的能量即为试样最终所吸收的能量。

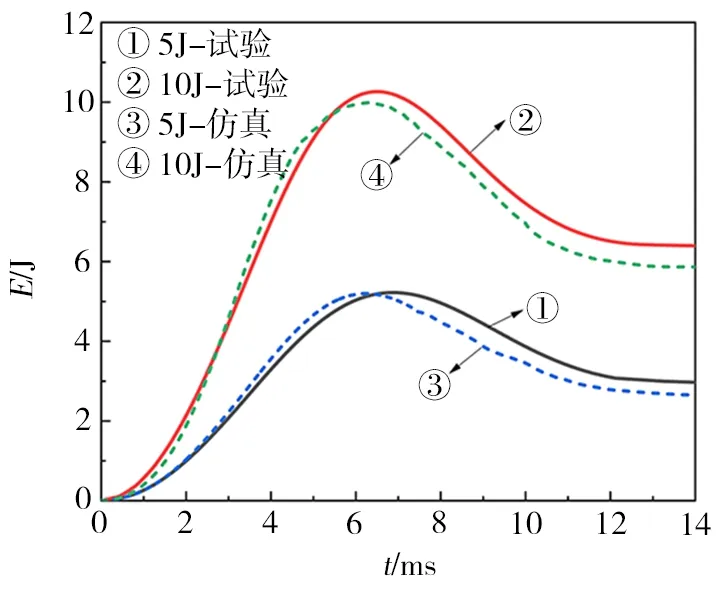
图10 吸收能量-时间曲线Fig.10 Absorbed energy-time curve

3.2.3 损伤形貌分析

图11 图12 为试样受冲击后的损伤形貌图，可以看出，冲击能量越大，试样损伤越严重。5 J能量冲击时损伤较小，对冲击正面目视时发现有轻微损伤，损伤区域呈菱形，该区域在光镜下观察到表面基体已出现裂痕，而对冲击背面目视时几乎观察不到损伤，在光镜下同样如此。10 J能量冲击时损伤严重，对冲击正面和背面目视时均观察到损伤。其中，冲击正面在目视的情况下观察到损伤从中心向两侧扩展，该区域呈长方形，光镜图片显示出纤维断裂。冲击背面的损伤更加严重，其纤维已被冲出表面，呈凸起状，损伤区域呈圆形，通过光镜可以观察到该区域出现了较为严重的纤维断裂以及纤维拔出。

图12 10 J能量的冲击损伤形貌Fig.12 Damage morphology under 10J energy

图13 图14 为试验与数值模拟的损伤对比图，在数值模拟中，5 J冲击的正面（图13）、10 J冲击的正面［图14（a）］和10 J冲击的背面［图14（b）］均产生了损伤，其与试验观察一致。损伤形状亦与试验一致，5 J冲击下的正面损伤和10 J 冲击下的背面损伤均聚集于冲击处，而10 J 冲击下的正面损伤向两侧扩展。表7对比了它们的损伤面积，所有冲击能量下损伤面积的误差均在10%以内，证明了本文所建立的多尺度模型的准确性与可靠性。

表7 试验与数值模拟损伤面积比较Tab.7 Comparison of damage area between test and numerical simulation

图13 5 J能量下试验与数值模拟正面损伤对比图Fig.13 Comparison of damage between test and numerical simulation at front side under 5J energy

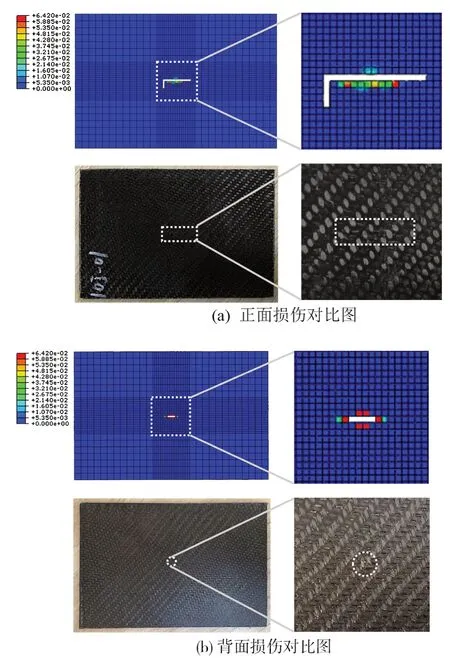
图14 10 J能量下的试验与数值模拟损伤对比图Fig.14 Comparison of damage between test and numerical simulation under 10J energy

4 结论

本文构建了一种基于基体和纱线塑性变形的微观-介观-宏观串行的多尺度模型，利用其预测斜纹机织热塑性复合材料的低速冲击损伤行为，并将其与试验结果进行对比，得到以下结论。

（1）微观-介观-宏观串行的多尺度模型考虑了微观尺度基体的塑性变形以及介观尺度基体和纱线的塑性变形，分别建立了基于抛物面屈服准则和Liu-Huang-Stout屈服准则的弹塑性损伤模型，能够准确地预测出斜纹机织热塑性复合材料的冲击损伤特性。

（2）两种不同能量下的低速冲击试验表明，冲击能量较大时材料冲击正面和背面均出现损伤，且损伤以纤维断裂为主。

（3）低速冲击数值模拟所预测的描述冲击损伤特性的冲击力-时间曲线、冲击力-位移曲线和吸收能量-时间曲线均与试验结果表现出良好的一致性，且数值模拟所得到的损伤面积与试验对比误差在10%以内。