基于粒子群算法的水库灌区输水灌溉管道布局优化方法
许 斌
(吉安市水利水电规划设计院,江西 吉安 343000)
水是人类生存必不可缺的物质,在农业生产、日常生活中有重要作用[1]。我国的淡水资源有限,分布差异较大,难以满足每个人的生产生存需求,随农业生产活动规模增加,我国出现了严重的水资源供求问题。研究表明[2],早在2013年,我国的农业灌溉用水总量就突破了3000亿m2,单位公顷的灌溉水量也超过了6000m3,尽管耗水量较高,但利用系数相对较低[3],局部地区的水资源利用系数甚至低至0.4[4]。提高灌溉水利用率不仅可以增加农业产量,还能解决目前严重的水资源供求问题[5],推动我国的农业发展。目前我国主要使用输水管道进行灌溉,因此,要想进一步提高灌溉水利用率,需要设计一种有效的输水灌溉管道布局优化方法。
输水管道灌溉具有几个显著特点,其一,灌溉相对方便;其二,易受灌溉水源的位置、环境等因素影响[6],其三,部分使用频率较低的管道布设成本较高。针对上述输水管道灌溉特点可知,输水灌溉成本主要包括管材成本和能耗成本[7],只有保证两者的配置最优化,且满足科学合理要求才能提高灌溉管道的应用效果。相关研究人员针对水库灌区灌溉管道布局特点设计了若干种常规的输水管道灌溉布局优化方法,主要通过调整管径,降低管网压力来排除地形、流量等对灌溉造成的影响[8]。受管网不同节点的灌溉特性动态变化影响,大多数灌溉管道布局方法的灌溉布局成本偏高,难以提高灌溉利用系数,因此,本文基于粒子群算法设计了一种全新的水库灌区输水灌溉管道布局优化方法。
1 水库灌区输水灌溉管道粒子群算法布局优化方法设计
1.1 基于粒子群算法构建灌溉管道布局优化模型
为了解决常规的灌区输水灌溉管道布局优化方法使用整数编码遗传函数布局寻优时受管道各布局节点管径动态约束影响[9],导致的管道布局灌溉成本偏高问题,本文基于粒子群算法构建了灌溉管道布局优化模型。粒子群优化算法可以假设一个随机搜索场景,将寻优的点位看成不同的粒子,确定优化函数的适应值,从而获取最优粒子解。在粒子群寻优的过程中需要预先进行PSO初始化,进行更新迭代,获取更新极值,此时的粒子更新式vi+1Ⅱ如式(1)所示。
vi+1Ⅱ=ωviⅡ+c1·r1·(pbestⅡ-presentⅡ)+c2·r2·(gbestⅡ-presentⅡ)
(1)
式中,ω—粒子的惯性权重;viⅡ—粒子的速度;pbestⅡ—粒子目前的位置;gbestⅡ—个体极值;presentⅡ—全局极值;c1、c2—学习因子;r1、r2—随机数。
结合上述的粒子更新式可以设置灌溉管道布局优化模型Ca,如下:
(2)
式中,p—管道布局维护费用;t—管道投资偿还时间;γ—管道连接状态;c—管道数量;l—管道管段长度,m;HP—管道灌溉系数;QP—泵基础流量,m3/s;P—灌溉扬程,m。
实际管道布局过程中,还需要考虑不同节点约束压力对布局结果造成的影响[10],因此本文设计了节点压力约束式,如下:
Pj≥Pjmin,j=1,2,3,…,m
(3)
式中,Pj—管道各个节点压力;Pjmin—各个节点的最低允许压力;m—管道节点数量。
此时根据各节点压力约束式,可以处理约束条件,将原有的目标函数转换成无约束优化问题,此时生成的粒子群布局适应度函数f,如下:
(4)
式中,M—管道优化布局正数。
根据上述的粒子群布局适应度函数可以进行管网管径布局统一,每个粒子位置矢量对应一条布局管线,对于离散的管径可以重新定义数组,有效地进行计算处理,当取值为0时,说明该管线可以去除。在管道布局的过程中可能会出现布局连续值,影响最终的布局优化结果,因此,本文对布局变量进行了离散化处理,调整了管径的编码,初步获取了管道的布局连接关系,粒子群算法的布局示意图如图1所示。
图1 粒子群布局示意图
由图1可知,通过上述的粒子群灌溉管道优化布局过程可以有效提高搜索精度,降低迭代问题对布局优化造成的影响。
1.2 利用MATLAB进行输水灌溉管道布局求解
使用上述的粒子群灌溉管道布局优化模型优化后,输水灌溉管道布局问题变成了一个近似规划线性问题,因此,本文利用MATLAB进行了编码解码处理,对上述模型进行了有效求解。求解的过程可以看成空间映射转换问题,通过相应的代码获取唯一解。首先需要设置MATLAB初始种群,进行随机选择,此时需要将产生的结构数据组合,构成一个结构群体,设置有效的进化参数进行迭代,获取符合求解要求的种群规模。
为了获取满足输水灌溉管道灌溉要求的布局成本最小值,需要设置约束条件,确定惩罚函数v,如下:
v=γmin{3hmax-2hmin}
(5)
式中,hmax—出口压力约束;hmin—管径压力约束。
使用上述惩罚函数可以得到相关的惩罚系数,此时可以设计求解遗传操作,对不同适应度个体进行随机采样,求解的布局概率Pi如下:
(6)
式中,f(xi)—个体的适应度。
根据布局概率可以确定获取解的相似性,选取最优布局保存策略,进行随机交换,此时可对比单点、两点、多点交叉的特点,获取基因幅度变化,设定控制参数,见表1。

表1 求解控制参数
由表1可知,对不同规模下的管道布局函数进行分析,获取控制参数,从而生成了MATLAB程序代码,如下SelCh=select(′sus′,Chrom,FitnV,GGAP),使用上述代码可以获取有效的灌溉管道布局解集,实现管道最优经济化布局。
2 实例分析
2.1 概况及准备
为了验证设计的基于粒子群算法的水库灌区输水灌溉管道布局优化方法的布局效果,本文选取X项目区进行实例分析,已知X项目区位于某市偏远区域,面积约234km2,地势高低差异大,由北向南呈阶梯状下降,地势最高点海拔为481m。X项目区属于温带季风气候,年平均气温适中,最高气温出现在7月。封冻期在11月下旬,湿润指数偏低,干旱指数偏高。其主要在夏秋两个季节降雨,冬季和春季易出现干旱,因此其种植的农作物为玉米,已知灌溉率为70%时玉米的亩产量最高。
本文选取的研究区域占地面积较大,可以将其划分为若干个灌溉单元,不同的灌溉单元需配置不同的泵房,前池尺寸与泵房尺寸需按照单元面积设置。X项目区的输配水管包括干管、支管等,项目区的布置示意图如图2所示。
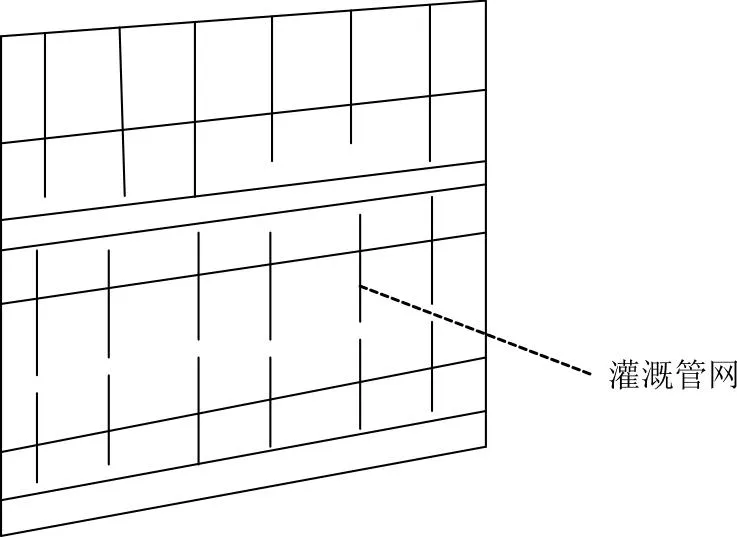
图2 X项目区布置示意图
由图2可知,X项目区设置了多个加压管网区,使用不同的方式泵水、供水,灌溉区设置水栓为240个,包括多个轮灌组。不同支管的灌水时间不同,拟定总灌水时间为165h。
X项目区使用对称灌溉法灌溉,每个干管的出水状态可以决定管网的压力均衡情况。此时可以使用MATLAB软件进行数据拟合,获取X项目区的造价拟合参数。已知管道灌溉布局费用主要由造价费用和泵运费用组成,因此,可以按照目标函数最小原则进行调整,设置不同的管段,每个管段的高程不同,此时可以预设轮组的划分方式,该项目工程不同管段的参数数据见表2。

表2 不同管段参数数据
由表2可知,结合上述不同管段的参数数据可以进行后续的管道布局优化实例分析。
2.2 应用效果与讨论
结合上述的概况及准备,可以进行管道布局优化实例分析,即使用本文设计的基于粒子群算法的水库灌区输水灌溉管道布局优化方法进行布局优化,记录不同管段的灌溉成本,将其与预设成本对比,实例分析结果见表3。

表3 实例分析结果
由表3可知,使用本文设计的基于粒子群算法的水库灌区输水灌溉管道布局优化方法进行布局优化后不同管段的灌溉成本均低于预设灌溉布局成本,证明本文设计的基于粒子群算法的水库灌区输水灌溉管道布局优化方法的布局效果较好,具有一定的经济价值。
3 结语
常规的输水灌溉管道布局方法缺乏有效的优化模型,布局效果较差,灌溉管道布局不合理,存在整体灌溉成本过高的问题,不符合目前的灌溉经济性需求。因此,本文基于粒子群算法,设计了一种全新的水库灌区输水灌溉管道布局优化方法。并通过实例分析,证明应用本文设计方法能够降低灌溉管道布局成本,具有一定的应用价值,为推动我国农业发展有重要意义。
但是本文未针对不同的灌溉方式(如喷灌、滴灌或洪灌)确定管道的尺寸和布置,还有更多的进步空间。因此在接下来的研究中,将重点关注不同的灌溉方式,完善本文方法,为水利工程可持续发展提供有效的技术支持。

