基于RBF神经网络的河道疏浚工程岸坡稳定性分析

曾秀娟，谢 涛

(赣州市水利电力勘测设计研究院，江西 赣州 341000)

现阶段随着我国经济水平的不断提高，交通运输行业越来越发达[1]。我国交通运输行业的重心已经由陆地扩大到海洋与河流。水利条件较为优越的城市开辟了越来越多的新航道，用以运载经济货物或乘客。随着我国航道数量不断增多，目前水运航道出现了较为饱和的情况，部分航道无法支撑其较大的运载需求，导致航道拥挤或运载效率低下等情况。为提高水运航道的运载量，需要对航道进行疏浚工程施工，即拓宽原有航道的宽度，增大水运航道的运载量。除此之外，部分天然航道存在由于缺乏科学的设计规划，导致航道堵塞，也需要对其进行疏通[2]。而在进行航道疏浚工程的过程中，为了防止海浪对建筑产生腐蚀作用，或者水体对建筑底部产生水压，导致建筑坍塌的情况，需要建造岸坡来保证内部工程的安全进行。岸坡可以隔绝水体与施工建筑，保护建筑不受海水的冲击，在河道疏浚工程中承担着十分重要的作用。然而现阶段，我国河道疏浚工程中岸坡存在经常失稳的问题，由于原料的限制，在正常阻挡水体侵扰时，岸坡自身的结构也会受到水体的冲击，导致结构不稳，出现变形或坍塌的情况[3]。如果疏浚工程持续时间过长，那么岸坡受海浪侵蚀的时间也会增加，将会加大岸坡崩落、崩塌的风险。因此需要在岸坡完工后对其稳定性进行分析，排查可能会影响岸坡坍塌的隐患，以此来保证河道竣工的施工能够顺利完成。同时，分析岸坡的稳定性也有利于对岸坡的失稳进行有效的预测与预防，做到在坍塌之前及时发现问题并采取补救措施，减少岸坡崩塌的风险，从而减少不必要的工程损失，保证施工人员的生命安全，提高河道疏浚的工程质量[4]。

但是当前使用的河道疏浚岸坡稳定性分析方法，存在分析误差较大、分析精度较低的问题，不利于河道疏浚工程的实际需求。为了解决这一问题，本文提出基于RBF神经网络的河道疏浚工程岸坡稳定性分析方法，以期为我国水利工程的建设提供一定的技术支持。

1 基于RBF神经网络的河道疏浚工程岸坡稳定性分析

1.1 建立RBF神经网络模型

RBF神经网络是一种具备单隐藏层的神经网络，可用于河道疏浚工程中对岸坡的稳定性进行预测与分析。对此首先需要建立基于RBF神经网络模型，具体建立步骤如图1所示。

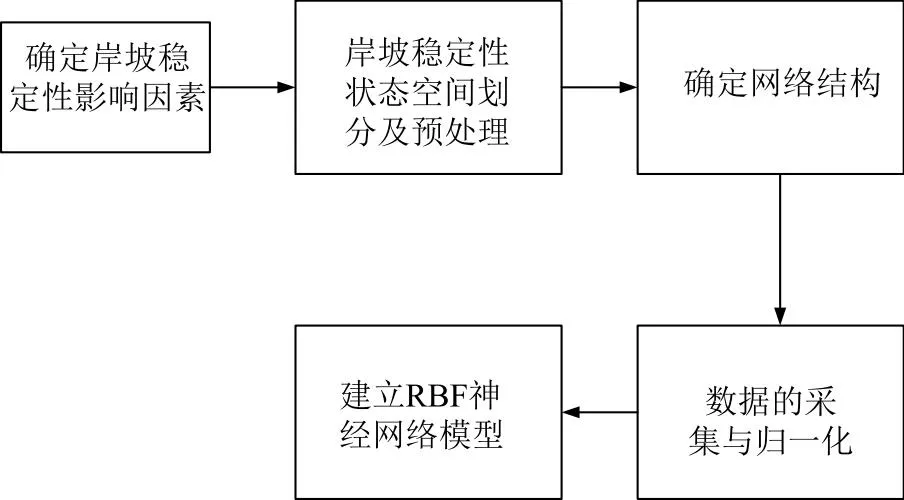
图1 RBF神经网络模型流程图

首先需要确定影响河道疏浚岸坡稳定性的因素，将该因素作为模型的输入参数[5]。在河道疏浚工程中，影响岸坡稳定性的因素一般可以分为岸坡高度、岸坡垂直高度与水平宽度的比值、单位容积内岸坡重量、岸坡荷载力、全反力与支持力的最大夹角、岸坡两端堤线的垂直距离、坡面泥沙凝聚力、单位重量内水体的机械能这8种。而根据灰色理论，可以将影响岸坡稳定性最主要的因素确定为全反力与支持力的最大夹角、岸坡两端堤线的垂直距离、坡面泥沙凝聚力、单位重量内水体的机械能和单位容积内岸坡重量这5个因素，将这5个因素作为主要预测因子输入进神经网络模型中，输入的神经元个数为5个。

在确定了影响岸坡稳定性的主要因素后，需要对岸坡的稳定性状态进行判断与划分，以便于神经网络模型能够更好的判断岸坡稳定性[6]。一般来讲岸坡的稳定性状态通常可以用“稳定”、“不稳定”、“极其不稳定”、“非常稳定”、“潜在失稳”等来进行描述，这里为了便于模型进行学习与判断，直接将岸坡空间状态分为“稳定”与“不稳定”两种状态，分别用0和1来表示。用稳定系数M来评价岸坡的稳定性状态，M通常是由多个岸坡相关的安全系数综合决定的[7]。根据河道疏浚工程岸坡设计方案，稳定系数的临界值一般取1.75，则可以得出稳定系数与稳定性的描述关系，即：

M≥1.75时为稳定状态，M<1.75时为不稳定状态。

因此，模型的输出参数为“0”或“1”，分别代表岸坡处于稳定状态或不稳定状态。而输入参数为5个，即岸坡稳定性的影响因素[8]。接下来需要对网络结构进行确定，在RBF网络结构中，除了输入层与输出层之外还包含一层中间层，需要对中间层的节点数量进行确定，节点数量如果过少，则模型无法实现复杂条件判断；节点数过多则会影响模型的判断准确性，经过科学测试，当中间层节点数为10个时，模型的训练与学习能力最强，因此将中间层节点数定为10，构建3层神经网络结构，具体结构图如图2所示。

图2 RBF神经网络结构图

为了提高模型的预测能力，需要为模型提供学习样本，即对岸坡数据进行采集与归一化。在历史工程案例中，选取最具代表性的岸坡参数做为模型的学习样本。在筛选过程中，注意要避免特征相同的样本数量过多，提高模型的学习效率与训练效率[9]。同时选取的参数需要覆盖所有岸坡的参数特征，保证模型能够进行全面的学习。在采集完基础数据后，需要对数据进行归一化处理，再输入进模型当中。所谓归一化就是将参数全部归至[0，1]的区间内，方便模型进行学习，对采集数据进行归一化可采取下列公式进行：

(1)

式中，x—输入的参数；X1—归一化后的数据；max—该参数能取到的最大值；min—其最小值。

对数据进行归一化后，即可将以归一化的数据输入至模型中进行学习与训练，利用BF算法对模型进行训练，具体流程如图3所示。

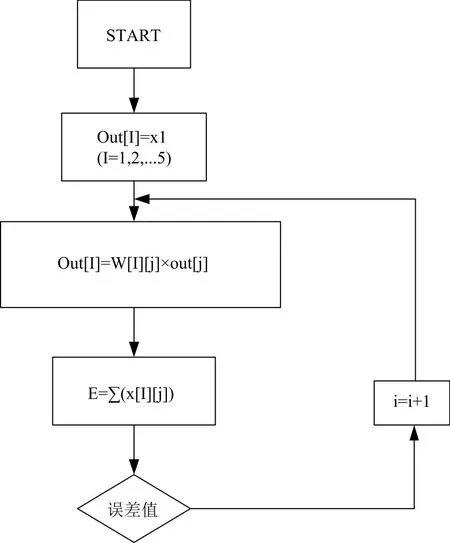
图3 RBF网络模型训练流程

根据上述流程对RBF神经网络模型进行训练，即可得到训练完成的网络模型，可用该模型对岸坡稳定性进行分析与预测。

1.2 岸坡稳定性分析

利用构建完成的RBF神经网络模型对岸坡稳定性状态进行分析，主要分为两部分。需要为模型提供大量工程样本供模型进行学习，构建影响稳定性因素与稳定状态之间的映射关系，使模型获得求解途径。待学习完毕后，即可将岸坡的各项指标输入进神经网络，模型会将其学习到的工程理论与指标进行匹配，通过自动学习与推理，对岸坡的实际结构状态进行分析。在此过程中还需利用圆弧滑动算法计算岸坡的变形量，具体公式如下：

(2)

式中，γ—岸坡偏移量，mm；q—岸坡土面宽度，m；b—岸坡顶部荷载力，N；W—荷载的标准重力值，N；α—岸坡水平线与弧线的夹角，(°)；P—岸坡中心到弧线圆心的垂直距离，m；Y—弧线的半径，m；∑M—因摩擦因素产生的转动力矩，N·m。

岸坡受到摩擦力产生的偏移量则为：

(3)

式中，γ1—岸坡因摩擦力产生的偏移量，mm。

岸坡在水平方向受到的地震摩擦力为：

(4)

式中，W—岸坡水平方向的地震系数；C—岸坡综合稳定系数；γ2—地震摩擦力，N。

岸坡水体分布压力值为：

(5)

式中，β—水体压力分布系数；c—水体凝聚力标准值，Pa；ς—水体分布压力值，Pa。则岸坡变形量可表示为：

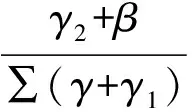
(6)

根据上述步骤即可计算出岸坡的变形量。将该变形量作为输入参数输入进RBF网络模型当中，即可完成对岸坡稳定性的分析。并根据上述公式计算结果，获取岸坡安全系数Fs，具体如下：

(7)

式中，f—岸坡载荷，N；Mi—块体的变形分量。至此，可通过岸坡安全系数，实现对河道疏浚工程岸坡稳定性的判断，完成基于RBF神经网络的河道疏浚工程岸坡稳定性分析方法的设计。

2 实验验证

为了更好地说明提出的基于RBF神经网络的河道疏浚工程岸坡稳定性分析方法在分析精度优于传统的分析方法，在理论方面设计完成后，进行实验测试环节，对该分析方法的实际分析效果进行分析。

2.1 实验环境描述

本次实验选取常规的岸坡稳定性分析方法作为对比对象，选用一个具有明显破坏迹象的典型库岸边坡作为分析对象，利用两种分析方法对其进行稳定性分析，最后与实际测量计算出的安全系数进行对比，通过比较分析方法与实际安全系数的拟合程度，来证明分析方法的分析精度。本次选取的库区岸边坡地质结构如图4所示。

图4 某库区岸坡地质结构图

根据上图可知，该岸坡积累的厚度在空间上呈现分布不均的特点，下伏基岩较厚，逆向岩层较薄，具体组成岩体成分为泥岩、石英砂岩和其他硅质岩。

选取的库区岸坡为中低山溶蚀地貌，岸坡宽度在900m以上，横断面间距为50m，非汛期时的水位线在240m以上，属于大型库区岸坡。勘探深度应达到最大冲刷深度以下3～5m，对卵石层不宜少于8m，对砂层不宜少于10m，基岩应进入中风化层不少于1m。在靠近岸坡边缘布置9个钻孔，15个探坑，钻孔深度应穿过可能坍岸面以下5m。整体坡度较为平缓，岩体露出较少，表面的植被发育完全。岸坡岩土层结构参数见表1。

表1 岸坡岩层结构

上述结构参数表可作为两种分析方法的主要数据支撑进行分析操作。同时为了提高实验结果的可靠性，考虑到实际施工过程当中天气的多变性，本次实验选择利用模拟软件对岸坡进行模拟降雨的操作，模拟在不同降雨强度下，岸坡参数的实际变化，记录在降雨环境下岸坡高度、岸坡垂直高度与水平宽度的比值、单位容积内岸坡重量、岸坡荷载力、全反力与支持力的最大夹角、岸坡两端堤线的垂直距离、坡面泥沙凝聚力、单位重量内水体机械能等参数，在此基础上利用两种分析方法对岸坡的稳定性进行分析，本次模拟降雨强度范围设定为0～200mm。

2.2 实验结果与分析

2.2.1模型样本训练

选择该水库工程的数据作为训练样本供RBF神经网络模型进行训练与学习。随机选取300组数据作为样本集，并按照260∶20∶20的比例，将样本集划分为训练集、预测集和验证集。经过7个训练周期，期望输出值为0.84，实际输出值为0.83，期望输出与实际输出值大小几乎相同，且相对误差较小，训练精度为98.7%，测试精度为96.4%，训练结果满足实验要求，可将模型应用至该水库工程岸坡稳定性分析之中。

2.2.2结果分析

以岸坡安全系数Fs为实验指标，得出库区岸坡安全系数计算结果如图5所示。

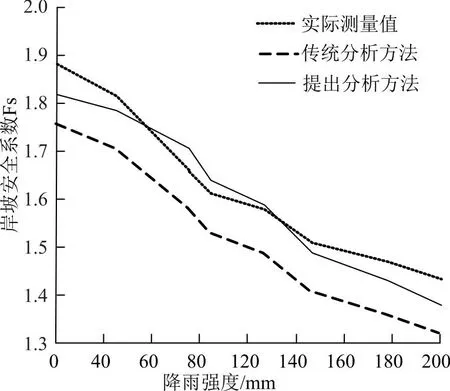
图5 库区岸坡安全系数计算结果

根据实验结果可知，岸坡安全系数会随着降雨强度的增加而有所变化。随着降雨强度的增加，岸坡的安全系数会逐步递减。当降雨强度超过200mm时，岸坡安全系数会下降到1.5以下。通过对比实际测量值与分析方法分析值的拟合程度，可以看出传统的分析方法分析出的岸坡安全系数与实际测量计算出的安全系数差距较大，说明传统的稳定性分析方法存在一定的误差，无法对岸坡的实际稳定情况进行准确分析。而提出的基于RBF神经网络的河道疏浚工程岸坡稳定性分析方法分析出的岸坡安全系数在与实际测量分析值的拟合程度上明显更高，说明提出的岸坡稳定性分析方法能够对岸坡安全结构等方面进行精确分析。

由此可以证明，本文设计的基于RBF神经网络的河道疏浚工程岸坡稳定性分析方法的分析精度更高。这是由于提出的岸坡稳定性分析方法建立了RBF神经网络模型，可以对通过实际参数对岸坡稳定性进行精准预测，能够满足河道疏浚工程中对岸坡的分析需求。

3 结语

本文所提出的河道疏浚工程岸坡稳定性分析方法与BRF神经网络结构进行了有效地结合，通过将岸坡变形量作为输入参数输入进神经网络模型中，实现对岸坡空间稳定性的智能化分析，极大地提高了分析的准确性，在分析结果上具有较高的科学度与可靠度。

但是由于时间的关系，本文在研究中没能考虑更多的影响河道疏浚工程岸坡稳定性的风险因素，因此在接下来的研究中，将对风险因素展开研究，为保障对河道疏浚工程中的施工人员的生命安全、减少不必要的工程损失、提高整体的施工质量，提供更多的技术支持。