一种基于静态贝叶斯的降雨诱发尾矿坝失稳评估模型

胡靖雯 聂 闻 芦 松 王震豪 Pooya Saffari

(1.中北大学理学院,山西 太原 030051;2.中国科学院福建物质结构研究所,福建 福州 350000;3.金属矿山安全与健康国家重点实验室,安徽 马鞍山 243000;4.青岛城市学院土木工程学院,山东 青岛 266071)

尾矿坝是一种用于堆放矿山废弃物的形似堤坝的构筑物,其中可能含有高浓度的可溶性重金属化合物。 作为一个高势能的危险源,其对矿山安全生产、生态环境和人民生命财产安全造成了巨大的威胁[1]。 我国现存尾矿坝12 655 座,具有数量大、新增多、高危坝分布多且广的特点[2]。 在所有尾矿坝失稳的致灾因素中,降雨是导致其失稳的主要因素之一,占据了尾矿坝失稳事故总量的24%[3]。 例如2010 年9 月21 日,强降雨导致了广东省银岩锡矿尾矿坝倒塌,造成22 人死亡,523 间房屋倒塌,直接经济损失达1 900 万元[4]。 2010 年10 月4 日,由于异常降雨,匈牙利Ajka 赤泥大坝发生灾难性坍塌,波及下游1 017 ha 的土地,致使367 处不动产受损,多人受伤[5]。 鉴于国内外尾矿坝溃坝的惨痛教训,我国对其安全运行愈发重视,对尾矿坝失稳的机理研究和预测愈发重要。

近年来,不少学者对尾矿坝的溃坝机制展开研究,为尾矿坝的安全管理提供了理论支撑。 宋志飞等[6]明确了尾矿坝子坝高度是尾矿沉积规律的主要外部影响因素。 YIN 等[7]在剖面模型试验的基础上,对尾矿坝不同高度、不同工况下的稳定性进行了分析,并考虑了尾矿坝堆积材料多层次的复杂特征。 部分学者运用数值仿真模拟方法预测溃坝,缪海波等[8]、侯永莉等[9]通过GEO-Studio 软件进行渗流模拟,李海港等[10]通过数值模拟试验,分析了尾矿坝的溃坝演化规律,然而数值仿真的边界条件理想化易造成结果失真。 随着机器学习算法的发展,学者们将其应用到尾矿坝领域:NIE 等[11]通过建立改良的水箱模型预测孔隙水压变化;DU 等[12]运用InSAR 时间序列对尾矿坝进行风险评估;王飞跃等[13]拟合浸润线观测孔水位与库水位的函数曲线,求得尾矿坝浸润线矩阵用于进行稳定性分析;李辉等[14]通过层次分析法和信息熵理论计算主客观权重,得到组合因子的辨识向量,根据置信度准则对尾矿坝的稳定性进行了评价。 由于尾矿坝失稳时其内部属性相互作用的复杂性与不确定性,传统的分析方法如故障树[15]、层次分析法[16]、事故树法[17]在解决问题的不确定性方面略显不足。 上述方法均无法有效解决各级事件之间的关联性,而分析各级事件之间的相关性在实际工程中十分必要。

贝叶斯网络(Bayesian Network,BN)是由美国加州大学PEARL[18]首次完整提出的一种不确定知识模型,该方法可以很好地弥补以上方法的不足。 BN作为一种概率模型,提供了一种直观方式表达大量相互关联变量的联合分布,变量代表了可能发生故障的原因、不同的故障模式及可能的后果[19]。 贝叶斯网络通过更新给定的观测值分布,以一致的概率方式表示不确定的结果,在电力系统评估[20]、房地产市场[21]、煤与瓦斯突出[22]等领域得到应用。 目前,贝叶斯分析先验概率的确定仍是凭借主观猜测[23],寻找先验概率科学的求解方法对提高结果精度至关重要。 本研究通过GeNIe 软件进行贝叶斯分析,预测尾矿坝在不同降雨量下各空间维度的失稳情况,分析不同降雨事件下尾矿内部属性的变动及相互作用机制,研究其失稳机理,并对其稳定性进行评价分析。

1 模型构建

1.1 基本原理

贝叶斯网络是一种非循环有向图及相关参数的集合,可通过逻辑推理解决不确定性问题[24]。 BN 由模型结构和相关参数组成。 图1 中每个节点对应一个系统变量,箭头代表直接的定性概率依赖,节点X1和X2是节点X3的父节点,节点X3是X1和X2的子节点。

图1 BN 网络示意Fig.1 Schematic of BN network

贝叶斯公式为

式中,P(X1)为标准化常量;P(X2)为先验概率;P(X1|X2)为似然率;P(X2|X)1为后验概率。

先验概率P(X2)反映的是在观测数据之前对其的认知[25]。 似然率PX1|X2()反映了在固定参数的情况下得到的某观测值的可信程度。 后验概率P(X2|X)1是贝叶斯网络预测结果,反映了在固定参数和模型的情况下对事件的知识。 标注化常量P(X1)可视为归一化系数。

1.2 概率拟定

由于BN 节点是布尔属性(Bool)的特点,即只有0、1 两种状态[26],故需将数据转译成概率代入BN 网络。 通过信息增益[27]选取特征在决策树分类算法中使用广泛,技术较为成熟,其通过计算所有特征值化分数据集得到,信息增益最高的特征值为最优值。

熵就是信息的期望值,即数据集的无序度,其值越小,变量的不确定性就越小,可进行如下计算:

式中,Hs为数据集的熵值;n为分类数目;pi为选择分类i的概率。

信息增益可由下式计算:

式中,D为数据集;A为特征;g(D,A) 为特征A对训练数据集D的信息增益。

现成的数据集可以较大程度上减少参数化BN所需的工作。 但是当数据集很小时,许多条件案例由于没有数据记录,没有足够的数据基础支撑条件概率的学习。 针对这一问题,ONISKO 等[28]提出了Noisy-OR 来减少条件概率数据需求的方法,并给出了Leaky Noisy-or gate 模型。 节点X的条件概率可表示为

式中,Xa为事件X的父节点之一;Pa为事件X与Xa的连接概率;Xc为所有未知因素的综合;Pc为事件X与Xc的连接概率;Xp为事件X的父节点的集合。

2 实例分析

2.1 工程概况

落木坑尾矿库地理坐标为东经114° 21′16″,北纬25°23′08″,根据《选矿厂尾矿设施设计规范》(ZB J1-90),该尾矿库为二等库,其基本参数取值见表1。

表1 落木坑尾矿库概况Table 1 General situation of Luomukeng tailings pond

该尾矿库所处区域气候温暖湿润,属于中亚热带季风湿润气候,年降水强度1 563 mm,全年最大降雨强度为61.7 mm/h,日降雨量最大为121 mm,年蒸发量为1 445.47～1 846.8 mm,降雨量及温度如图2 所示。 尾矿坝所处区域降雨量较大,雨水对其稳定性的影响不容忽视。

图2 大余县2020 年降雨量及气温Fig.2 Rainfall intensity and temperature in Dayu County in 2020

2.2 模型试验

本研究采用物理堆坝模型试验重建尾矿坝的堆积过程[29],落木坑尾矿库的鸟瞰图如图 3(a)所示。根据尾矿库现场的情况和实际研究的可行性,确定模型比尺为1 ∶100。 模型长约13 m,宽7 m,高1.5 m,倾角约35°。 尾矿坝由1 个初级坝和4 个子坝组成。建坝初期,采用自下而上递增的方法,修建了4 级子坝。 初级坝采用红黏土建造,4 个子坝的材料是从落木坑尾矿中收集的尾矿。 试验模型如图3(b)所示。

图3 落木坑尾矿库Fig.3 Luomukeng tailings dam

在堆坝模型试验的基础上,采用专用的降雨模拟装置,再现降雨过程对尾矿坝的影响。 本研究尾矿坝模型试验系统主要由4 部分组成,即山地模型、放矿系统、供水系统、降雨系统,如图4 所示。

图4 试验模型照片Fig.4 Photos of the experimental model

为了模拟大坝尾矿的堆积过程,将尾矿浸泡在少量的水中,并放置在一个大塑料桶中。 尾矿沿塑料桶底部直径8 cm 的PVC 管注入尾矿池。 降雨设备由6组相同直径的喷嘴组成(每组6 个喷嘴),降雨强度可以在0 到100 mm/h 之间变化。 参考中国气象局颁布的降雨强度等级,结合试验实际情况划分标准,试验的降雨强度分为15、25、35 mm/h 3 个等级。 降雨设定持续时间为10 min,关闭降雨设施后,每级坝20 cm 深处随机取样测量实时含水率。 取样方法为每级坝随机取3 个样品,共12 个样品,样品质量为3 kg,取样位置如图3(b)所示,将样品装入塑料袋中进行后续的试验测试。 取样后,取样产生的孔洞用相同的材料填充。 等待模型排水完毕,进入下一个降雨模式,重复前面的步骤,直到完成3 组降雨测试试验。分别在每级坝体内部埋设4 个孔隙水压计,位置沿坝体中轴线剖面布设,以初级坝为基准点,计算获得不同降雨量下不同区域的尾矿初始浸润线高度。

根据《试验室玻璃器皿密度计》(GB/T 21785—2008)进行了比重计试验,试验仪器为TM85 尾矿密度仪。 根据《煤炭筛分试验方法》(GB/T 477—2008)进行筛分试验,装置为GZS-1 型高频振动筛。 大雨时部分尾矿的级配曲线如图5 所示。 由图5 可知:不同高度尾矿的材料非均质特性明显,各级坝的级配曲线在尾矿粒径为0.002～0.600 mm 时差异较大。 尾矿位置越高,颗粒级配曲线越陡,尾矿的粒径比较均匀。

图5 大雨时尾矿的粒径级配累积曲线Fig.5 Cumulative curve of particle size gradation of tailings during heavy rain

根据《土壤检测第23 部分:土粒密度的测定》(NY/T 1121.23—2010),利用环刀法测量尾矿的密度。 直剪试验依据的规范为《土工试验方法标准》(GB/T 50123—2019),采用的设备为ZJ 应变控制直剪仪,通过直剪试验获得样品的黏聚力c和摩擦角φ。 限于篇幅,部分参数取值见表2。 由表可知:降雨量越大,浸润线位置越高;高处的尾矿黏聚力较小,摩擦角略小,含水率较大,密度较低。

表2 部分参数取值Table 2 Values of part parameters

3 基于静态贝叶斯的尾矿坝稳定性分析

基于尾矿库各参数自身的性质将其划分为两类:物理参数,包括浸润线、密度、含水率;力学参数,包括黏聚力、摩擦角、抗滑力和滑动力。 通过查阅相关资料[30],基于各参数的逻辑关系,建立了如图6 所示的模型。 为了丰富样本数据,提高信息增益的准确性,针对每个节点进行拉格朗日多项式插值[31]。 通过选取信息增益最高值划分数据集,并将其作为预警值判断每个节点的状态,据此计算先验概率。 由于贝叶斯模型以安全因子为标准评判坝体是否失事,故选择该值作为评价指标划分各个参数区间。 以密度为例说明求取过程,当安全因子为1 时密度值就是该参数的预警值。 按照式(4)计算信息增益,密度最小值为2.32,为了保证结果精度,从2. 32 开始,每次增加10-6,直至计算到最大值2.99。 当信息增益值最大达到2.750 001 时,该值即为密度的区间划分值。 计算出密度大于该值的概率占总体的31.42%,该值即为尾矿失稳时密度的先验概率。 各个节点状态如图6所示,箱子下方左右两侧数据分别表示数据的最大和最小值,中间数据表示该节点的预警值,箱中百分比为先验概率。

图6 节点状态Fig.6 Node status

当节点值大于预警值时,即Xi=1,节点处于危险状态;反之,Xi=0,节点处于安全状态。 将坝体稳定即“坝体失稳”节点的状态为“0”作为标准学习各个节点的状态。 以抗滑力为例说明建模过程,设含水率为事件X,设其父节点降雨,高度分别为X1,X2。 基于模型试验,将降雨分为小中大3 个等级,分别为X1=1,X1=2,X1=3,假设发生各降雨量的概率相等,每个等级的降雨量发生概率为33. 33%。 尾矿坝为四级坝,分别为X2=1,X2=2,X2=3,X2=4,将每级坝的概率设为25%。 统计X=1 时各个节点的状态,计算的概率参数见表3。

表3 含水率的概率参数Table 3 Probability parameters of the water content

将含水率的概率参数代入式(5)中,计算含水率的条件概率。 含水率在一二级坝时的条件概率见表4。

表4 含水率的条件概率Table 4 Conditional probability of water content

根据《尾矿库安全规程》(GB 39496—2020),将尾矿的安全系数划分为4 个等级(表5)。

表5 尾矿安全系数及其状态Table 5 Safety factor and status of tailings

将所有节点的条件概率输入建立的网络中,各节点的右下角会出现“√”脚标,得到如图7 所示的模型,State 0 表示该节点仍处于安全状态,State 1 表示该节点处于危险状态。 本研究尾矿坝表层发生失稳,滑动力、抗滑力及安全系数的计算采用无限边坡模型[32]:

图7 贝叶斯条形图Fig.7 Bar graph of Bayesian

式中,β为潜在的滑动面倾角,(°);ρ为土体平均密度,g/cm3;H为土面至破坏面的深度,m;c′为潜在滑动面的有效土壤黏聚力,N/m2;φ′为潜在滑动面的有效摩擦角,(°);PWP为潜在滑动面的孔隙水压力,Pa。

为了模拟潜在失稳效果,在试验初期设置了较高的尾矿库库区水位线,因此计算的失稳概率会普遍偏高。 展示各个降雨事件下不同空间位置的尾矿参数的贝叶斯结果如图8 所示。 小雨时,各级坝几乎处于稳定运行状态;中雨时,尾矿坝虽然稳定概率较高,但与小雨相比,其稳定运行的概率有所降低,尾矿坝有局部失稳风险且失稳的概率略有增加;与小雨和中雨条件下的尾矿坝情况相比,大雨时其失稳的概率增高,一级坝稳定运行的概率较大,其余子坝极有可能处于临界失稳状态。 综合分析得到如下结论:

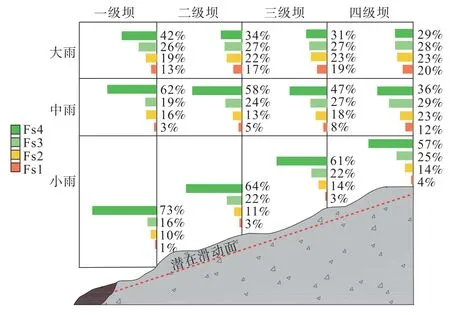
图8 尾矿坝失稳分析结果Fig.8 Results of instability analysis of tailings dam

(1)降雨量增加导致尾矿坝失稳风险明显加大。结合表2 分析原因:降雨量增加使得更多的雨水入渗到尾矿中,导致含水率增长和浸润线抬升;含水率增长也将进一步导致浸润线上升;雨水入渗坝体,填充了尾矿骨架之间的孔隙,尾矿单元内的水量增加,含水率较大。 水的润滑作用使尾矿的黏聚力降低,抗滑力下降,坝体更易失稳。

(2)同等降雨条件下,尾矿位置越高,其失稳的概率越大。 结合图5 分析可得,不同高度尾矿的材料非均质特性明显,高处尾矿的尾矿粒径均匀,缺乏小颗粒填充大颗粒之间形成的孔隙,颗粒之间距离比较远,单位面积上土粒的接触点少,颗粒之间的咬合作用较弱,黏聚力较小;雨水迸溅和径流冲刷导致尾矿表面颗粒向下迁徙,加剧了不同空间位置尾矿的差异性。 高处颗粒缺失,密度较低,影响尾矿的摩擦角;因此,尾矿抗滑力降低,失稳概率增加。

4 结 论

本研究以江西落木坑尾矿坝为例,通过1 ∶100 大比尺模型试验获取不同降雨量下尾矿的浸润线、黏聚力、摩擦角、含水率和密度的样本数据,并利用无限边坡模型计算了滑动力、抗滑力和安全系数。 结合信息增益和Leaky Noisy-or gate 模型,建立了一种新的基于贝叶斯的尾矿坝稳定性评估模型,阐明了尾矿坝的失稳机理,预测了不同降雨事件下不同空间位置的尾矿坝的状态。 所得结论如下:

(1)相较于传统的贝叶斯分析,通过信息增益计算先验概率大大降低了模型分析的主观性。相较于其他不确定性分析方法,使用Leaky Noisy-or gate 模型求各节点之间的条件概率,降低了因节点信息缺失或失真造成的偏差,极大提高了模型计算精度。 通过GeNIe 软件建模,实现了结构和参数的自学习,发挥了该软件在贝叶斯推理方面的显著优势,并可以通过结果进行反推,追溯坝体破坏的原因。

(2)降雨量对尾矿参数变动有着显著影响,并且随着降雨量增加,各参数之间的相互作用更加明显。降雨量增加使更多雨水入渗到坝体中,导致尾矿含水率增长和浸润线抬升,含水率增加又将导致浸润线进一步上升以及黏聚力降低。 由于尾矿坝空间非均质特性,坝体高处粒径均匀,本就容易失稳,而雨水迸溅和径流冲刷造成的坝体侵蚀将差异变得更大,高处尾矿的失稳风险进一步加剧。 降雨通过改变尾矿的物理参数影响力学参数,从而改变坝体稳定性。

(3)本研究所建模型的分析结果与试验实测记录相符,说明该模型有一定的可靠性,可适用其他工况下的坡体稳定性分析。 不足之处是该模型没有考虑时态作用下尾矿坝稳定性各影响因素的变动,鉴于动态贝叶斯在描述随机演化不确定关系方面的优势,下一步考虑将贝叶斯网络与时间信息相结合,形成一种可处理时序数据的随机模型。