一种基于偏度和峰度联合检测的频谱感知算法*

谭哲雯,雷可君,杨 喜,汪旭明,谭宇豪

(吉首大学通信与电子工程学院,湖南 吉首 416000)

随着无线通信技术迅猛发展,无线终端设备对频谱资源的需求与日俱增.在这种背景之下,频谱资源短缺成为无线通信领域亟待解决的问题.针对这一突出问题,目前有2种解决方案可供选择:一是挖掘尚未开发利用的频谱资源,如THz与可见光等频率较高的频段,二者有望应用在下一代移动通信技术中;二是多项调查报告显示,传统频谱分配方案使得授权频谱资源利用效率普遍较低[1-3],故可充分利用这些空闲的授权频谱.认知无线电(Cognitive Radio,CR)技术通过有效感知闲置频谱并允许次级用户动态接入,能极大提升现有频谱资源的使用效率.CR技术可以利用频谱空穴,其原理在于非授权用户伺机访问已授权的频谱资源,即非授权用户在特定的时间和位置,使用授权用户并没有占用或没有充分利用的频谱资源,从而提升频谱使用效率.次级用户通过检测授权主用户的频谱占用情况来找到频谱空洞的过程,称为频谱感知[1].在CR网络中,次级用户不能因为切换到一个可用的频谱上而干扰到主用户.与此同时,次级用户应该高效识别和利用频谱空洞,以提高认知网络的吞吐量和服务质量.因此,频谱感知算法的检测性能对主用户通信和CR网络都至关重要.

典型的频谱感知算法包括能量检测[2]、匹配滤波器[3]、循环平稳特征检测[4]等.但是这些方法都有各自适用的特定场景及应用上的缺点,如次级用户需要事先知道主用户信号、传输信道或者噪声的部分/全部特征,显然这些信息在实际的通信过程中难以获得.为了克服这些困难,有学者提出了一类基于Jarque-Bera(JB)检测的频谱感知算法[5-8],该类算法通过检验接收信号是否服从高斯分布来判断信道占用情况,并采用偏度和峰度参数作为检测依据.这些算法无需接收信号及传输信道的统计参数等先验信息,可以很好地克服上述3种经典算法存在的问题.遗憾的是,这些算法局限于渐近条件下,需要很大的样本数目才能获得可靠的感知结果,因而极大地限制了算法的应用.为了提升有限样本条件下的检测精度,笔者拟设计一种全新的基于接收信号偏度和峰度联合检测的频谱感知算法(简称“联合检测算法”).该算法利用归一化的样本偏度和样本峰度构造统计判决量,可以有效拓展JB类检测算法的适用范围.

1 感知判决模型

设认知用户采样的接收信号X=(x(1),x(2),…,x(NS)).在CR中,为了检测主用户信号,建立以下二元假设检验模型:

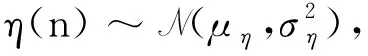
(1)

在无线传输过程中,信号受到多径衰落的影响,因而当信道被占用时,s(n)的概率分布情况取决于多径衰落信道模型.以常用的瑞利(RAYLEIGH)信道为例,s(n)的概率密度函数

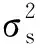
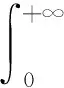
其中“*”表示线性卷积运算.由此可得[5]

(2)

其中Φ(x)是标准正态随机变量的累积分布函数.对比(1)和(2)式可知,由于主用户信号的加入使得H1状态下接收信号的分布明显区别于H0状态下的高斯分布,因此可以通过检验接收信号的分布来判断主用户信号是否出现,由此建立以下二元假设检验模型:

(3)

有必要指出,以上是以瑞利信道接收信号为例来说明基于统计分布进行频谱感知的适用性,(3)式同样适用于其他非高斯主用户接收信号的检测场景.

2 偏度和峰度联合检测及判决门限的计算

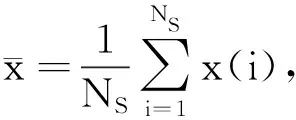
(4)

(5)

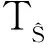
(6)

当TX接近0时,可以认为只有高斯噪声存在;当TX大到一定程度时,可以认为是主用户信号的出现导致该值发生变化,由此判断授权信道被主用户占用.于是,正态性检验问题(3)转化为二元假设检验问题

相应地,判决规则表述为:比较检验统计量TX与判决门限λ,若TX≥λ,则判断主用户信号存在;否则判断主用户信号不存在.判决门限λ的设置由目标虚警概率及其统计分布共同决定.

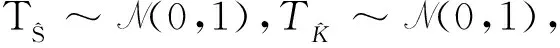
从而可得联合检测算法的虚警概率

经计算得到

由此可得判决门限的表达式

(7)

联合检测算法的流程如下:

(ⅱ)根据(6)式计算感知判决TX.

(ⅲ)根据(7)式计算感知判决门限λ.

(ⅳ)判决:若TX≥λ,则判断主用户信号存在;否则判断主用户信号不存在.

由于联合检测算法感知判决量和门限的计算均不依赖于信道及噪声参数,因此它是一种全盲主用户信号检测算法,可以有效解决噪声不确定等问题.

3 仿真实验

仿真过程中,目标虚警概率设置为0.1,样本数目N设置为30,80,200,所有仿真结果均经5 000次Monte-Carlo实验得到.图1给出了联合检测算法与经典的JB频谱感知算法的检测概率对比结果.

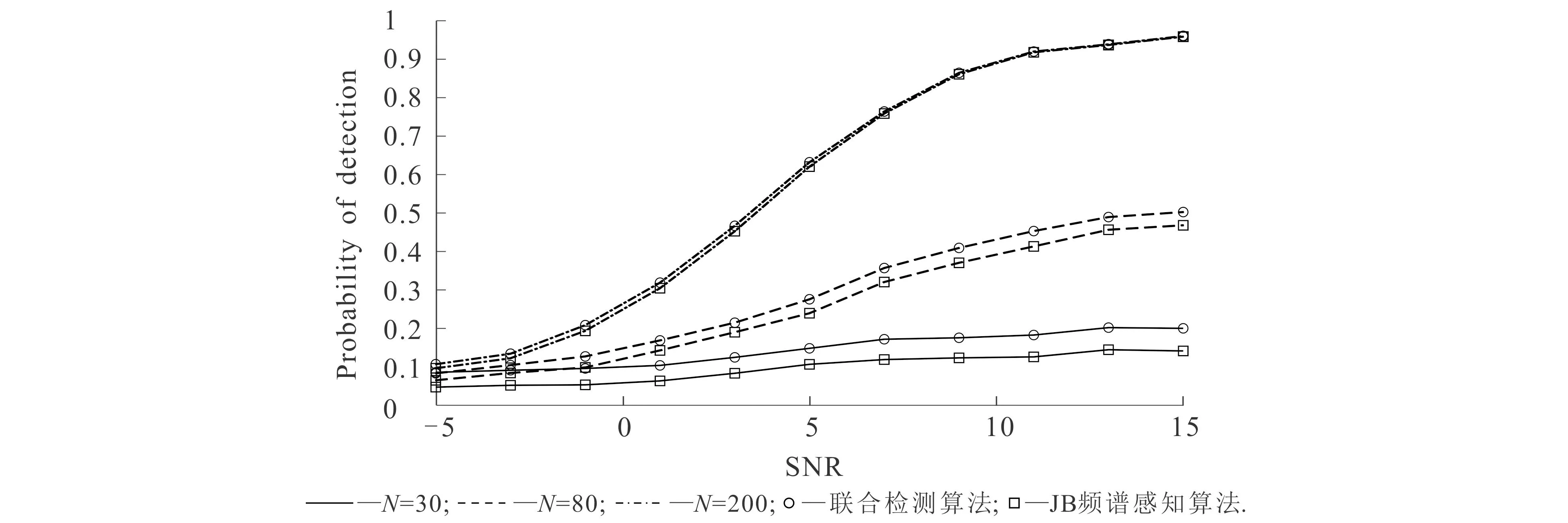
图1 不同信噪比和样本数目下2种算法的检测概率Fig. 1 Detection Performance of the Algorithms with Different Numbers of Samples and Signal-to-Noise Ratios

从图1可知,在不同样本数目下,联合检测算法的检测概率比JB频谱感知算法的高,特别是在小样本条件下表现得更明显;随着样本数目的增加,2种算法的检测概率曲线接近重合,特别是在高信噪比条件下.由此可知,与JB频谱感知算法相比,联合检测算法在小样本的检测条件下更具优势.

表1给出了目标虚警概率为0.1时,不同信噪比和样本数目下2种算法的实际虚警概率.

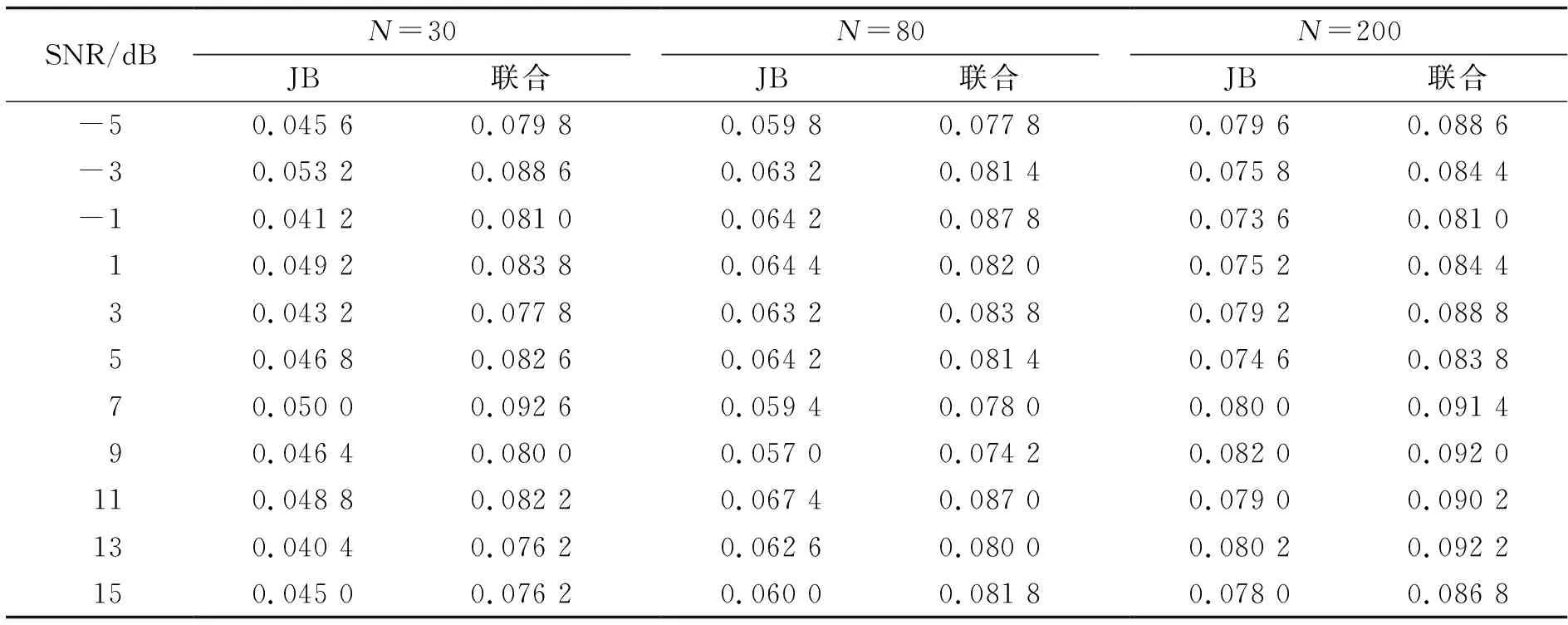
表1 不同信噪比和样本数目下2种算法的实际虚警概率Table 1 Actual Probability of False Alarm of the Two Algorithms with Different Signal-to-Noise Ratio and Numbers of Samples

从表1可知,在不同样本数目下,与JB频谱感知算法相比,联合检测算法产生的实际虚警概率更接近目标虚警概率0.1,说明其获得的感知判决结果更可靠,感知性能更优.

受试者工作特征(Receiver Operating Characteristic,ROC)曲线是另一个评价检测算法性能的有效工具.样本数目设置为50,80,100,图2展示了信噪比为8 dB时2种算法的ROC曲线.注意到在实际的CR中,目标虚警概率通常设置为较小的值,因此图2只给出虚警概率为0～0.5时的结果.

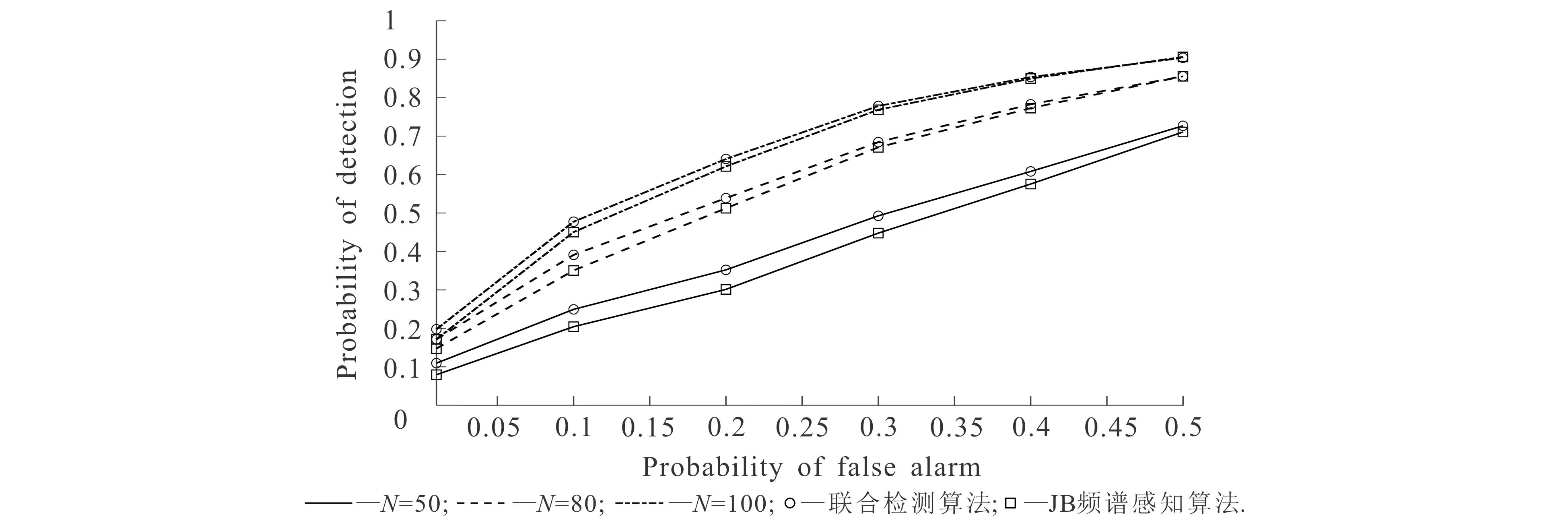
图2 不同虚警概率和样本数目下2种算法的检测概率Fig. 2 Detection Probability for the Two Algorithms with Different Numbers of Samples and False Alarm Probability

从图2可知:在小样本条件下,联合检测算法的ROC性能曲线明显优于JB频谱感知算法;随着样本数目的增加,2种算法的检测概率曲线接近重合,特别是在高虚警概率条件下.由此可知,与JB频谱感知算法相比,联合检测算法在小样本的检测条件下性能更高.

4 结语

经典的JB频谱感知算法采用渐近条件下的分布结果进行设计,使得在小样本条件下,算法的理论判决门限与真实判决门限之间存在较大偏差,这既降低了检测结果的可靠性,也限制了算法性能的提升.为了解决这一问题,笔者设计了一种基于偏度和峰度联合检测的频谱感知算法.该算法利用归一化的样本偏度和样本峰度构造感知判决量,并考虑有限样本数目的影响,是一种非渐近条件下理论判决门限的计算方法.仿真结果表明,相比JB频谱感知算法,联合检测算法产生的感知判决结果更可靠,且在小样本检测条件下获得的检测概率更高.