不同参数条件下抗滑桩的力学性状分析

高超

【摘    要】：为了研究不同参数抗滑桩对边坡加固效果的影响，选取不同截面形状抗滑桩分别在相同截面积、抗弯刚度、不同桩间距和相同抗弯刚度、不同截面面积两种情况进行数值模拟，运用强度折减法对桩-边坡体系进行计算，分析安全系数随抗滑桩截面形状、桩间距、截面面积的变化趋势，发现抗滑桩截面边数目与边坡加固效果之间的必然联系，揭示不同截面形状、截面面积和桩间距对抗滑桩内力、边坡位移的影响规律。

【关键词】：抗滑桩；桩间距；截面形状；抗弯刚度；边坡加固

【中图分类号】：TU473.1【文献标志码】：A【文章编号】：1008-3197（2023）02-19-08

【DOI编码】：10.3969/j.issn.1008-3197.2023.02.005

Analysis of Mechanical Properties of Anti-slide Pile under Different Parameters

GAO Chao

（China Railway Design Corporation， Tianjin 200063， China）

【Abstract】：In order to study the influence of different parameters of anti-slide pile on the slope reinforcement effect， the paper selectes anti-slide piles with different section shapes for numerical simulation under the two conditions of the same sectional area， bending stiffness， different pile spacing， same bending stiffness and different section area. By using the strength reduction method to calculate the pile-soil unit， the paper analyzes the variation trend of safety coefficient with section shape， pile spacing and section area of anti-slide pile， discovers the inevitable relation between the number of sides of anti-slide pile section and the reinforce effect of slope and reveals. The influence law of different section shapes， section areas and pile spacing on internal force and slope displacement of anti-slide piles.

【Key words】：anti-slide pile; pile spacing; cross-section shape; flexural rigidity; slope reforcement

抗滑樁以抗滑能力大、桩位布置灵活、支挡防护效果好等特点，被广泛应用到各种边坡防护工程。实际工程中，抗滑桩截面形状多种多样，桩间距布设等也没有确定的方案，研究抗滑桩截面形状、桩间距、截面面积等参数对维护边坡稳定、降低工程造价等具有重要意义。目前，国内外已有不少学者开展了抗滑桩不同参数对边坡加固效果影响的相关研究。Cai F等[1]、 Ugai K等[2]对桩-边坡体系进行了相应的理论计算并对抗滑桩部分参数进行了分析，发现抗滑桩抗弯刚度和桩顶条件对边坡稳定性影响比较大，合理设计锚固端长度可有效降低成本。周记名[3]、司光武[4]、朱兴帅[5]、李贤等[6]、郑百录等[7]、年廷凯等[8]借助数值模拟、模型试验等方法，就不同截面形状抗滑桩的受力以及破坏机理进行了研究，发现矩形和圆形群桩承受滑坡推力基本相近，对桩间土拱效应的形成有一定影响；圆形抗滑桩在施工过程中安全性更高，而矩形抗滑桩的受力更好。李浩等[9]、丁桥军等[10]、谢明星等[11]采用单因素分析法，研究了不同桩间距对边坡位移、安全系数、桩身土压力等的影响，发现桩间距变化对桩身弯矩影响较小，不同深度桩身土压力受桩间距的影响较为明显。

目前对抗滑桩截面形状的研究大多集中于矩形和圆形，对正方形、正六边形、正五边形等不同截面形状抗滑桩加固效果的研究较少，针对抗滑桩加固效果与截面边数、截面面积、抗滑桩截面形状与合理桩间距间的相互联系也没有定论，本文选取5种截面形状和5种桩间距，研究不同参数抗滑桩对边坡加固效果的影响规律。

1 模型建立

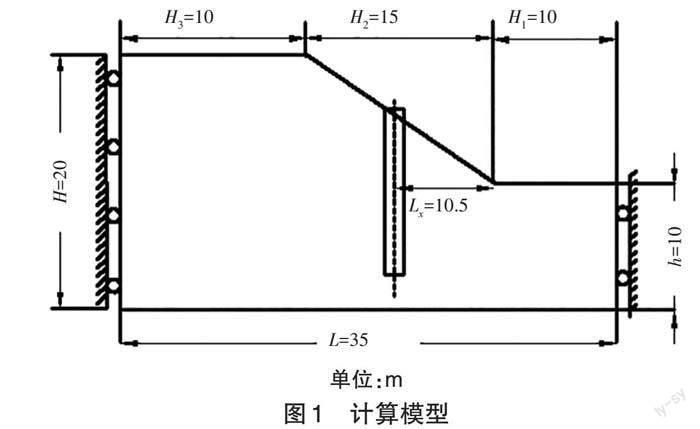
采用典型边坡算例[12～13]，抗滑桩加固于主滑区，模型长L为35 m、高H为20 m、进深W为10 m，主滑段坡比为1∶1.5，滑坡体抗滑区水平长度L1为10 m，主滑区长L2为15 m，后缘区长L3为10 m；抗滑桩长度统一取Lp为15.5 m，桩心距坡脚水平距离LX为10.5 m，桩心间距S分别取3、3.5、4、4.5、5 m。见图1和表1。

选取截面面积为1 m2，截面形状为正方形、长方形、正六边形、正五边形、圆形，桩间距为3、3.5、4、4.5、5 m研究不同截面形状抗滑桩在不同桩间距下边坡加固效果；选取截面形状为正方形、长方形、正六边形、圆形研究相同抗弯刚度、不同截面形状的抗滑桩在不同横截面积下边坡加固效果。建立模型时遵循参数一致原则，共需建立29个分析模型。见图2。

模型四周边界均为约束法向位移，底面为固定约束。桩-边坡体系以桩体侧面和底面为主控面，岩体表面为从属面，采用面面离散分析，法向定义为硬接触，切向摩擦系数均设为0.51，桩与岩体均采用六面体、C3D8单元进行计算。见表2。

2 计算结果分析

2.1 抗滑桩参数对安全系数影响

对数值模型进行强度折减，计算不收敛时安全系数随抗滑桩截面形状和桩间距变化关系。见表3和图3。

桩间距相同，随着抗滑桩截面边数的增加，安全系数逐渐降低，当边数趋近无线多时，截面形状趋近圆形，此时安全系数最小。若边坡滑动方向已知，长方形抗滑桩为最优选择；若滑动方向未知，正方形抗滑桩为最优选择。由于抗滑桩塑性变形较小，可近似看做刚性挡墙，在滑动方向已知的情况下，垂直滑动面边与平行滑动面边比值越大，墙面越宽，滑动位移越小，抗滑能力越强，安全系数越大。

截面形状相同，随着桩间距逐渐增大，安全系数逐渐减小，当桩间距无限大时，相邻两桩互相影响忽略不计，可近似看做单桩作用，此时安全系数最小。截面形状为正方形和长方形、桩间距＜4 m时，安全系数变化趋势较慢；桩间距超过4 m后，安全系数下降趋势较快；桩间距宜设为4 m。截面形状为正五边形和正六边形、桩间距＜4.5 m时，安全系数变化较小；超过4.5 m时，安全系数变化较大；桩间距宜设为4.5 m。截面形状为圆形时，为防止边坡失稳，桩间距宜≥5 m。不难发现，随着截面边数逐渐增大，最优桩间距有逐渐递增，当桩间距过分增大，会导致边坡稳定性反而下降；因此抗滑桩间距应在一定范围，与工程实践相符。

2.2 抗滑桩接触应力随抗滑桩参数变化规律

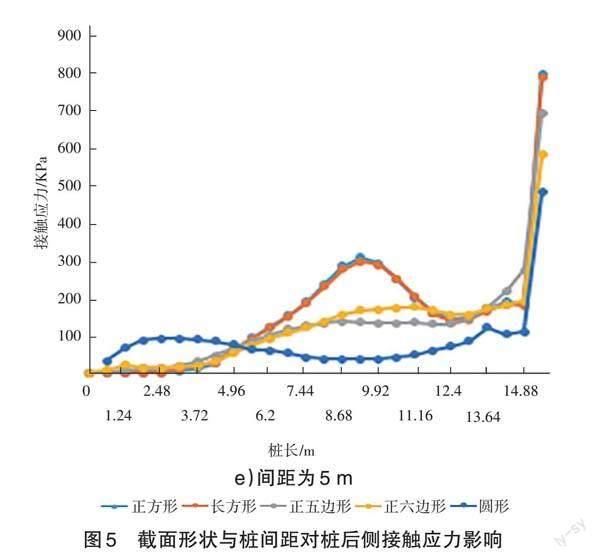
以抗滑桩前后为路径，分别提取计算结果不收敛时桩两侧的接触应力。见图4和图5。

抗滑桩底应力较集中且不受截面形状和桩间距的影响。在工程实践中，为防止应力过大造成底部折桩，应适当增加抗滑桩底部强度。桩间距对抗滑桩应力分布情况几乎没有影响，截面形状对抗滑桩应力分布有较明显影响；桩前和桩后随桩间距的变化趋势基本相同，但桩前接触应力近似为桩后接触应力的2倍，这是由于抗滑桩型心距离坡脚水平距离较大，而距离坡顶水平距离较小；另外，相同桩间距下，正方形最大接触应力最大，圆形接触应力较小，间接可以说明随着截面边数增加，接触应力出现逐渐缩小的趋势。

接触应力均在距桩顶4～12 m出现较大波动，整体应力峰值均随桩间距增大出现减小的趋势，增大到一定程度接触应力变化趋于平缓。截面形状为正方形和长方形、桩间距＜4 m时，接触应力减小趋势较为明显，超过4 m后变化幅度较小；截面形状为正五边形和正六边形、桩间距＜4.5 m时桩两侧接触应力变化较小，超过4.5 m时变化幅度较大；截面形状为圆形、桩间距3～5 m范围内接触应力均有较明显减小趋势；因此圆形抗滑桩间距应＞5 m。接触应力随桩间距变化规律基本与安全系数随桩间距变化情况相符，证明了结论的可靠性。

2.3 坡体变形随抗滑桩参数变化规律

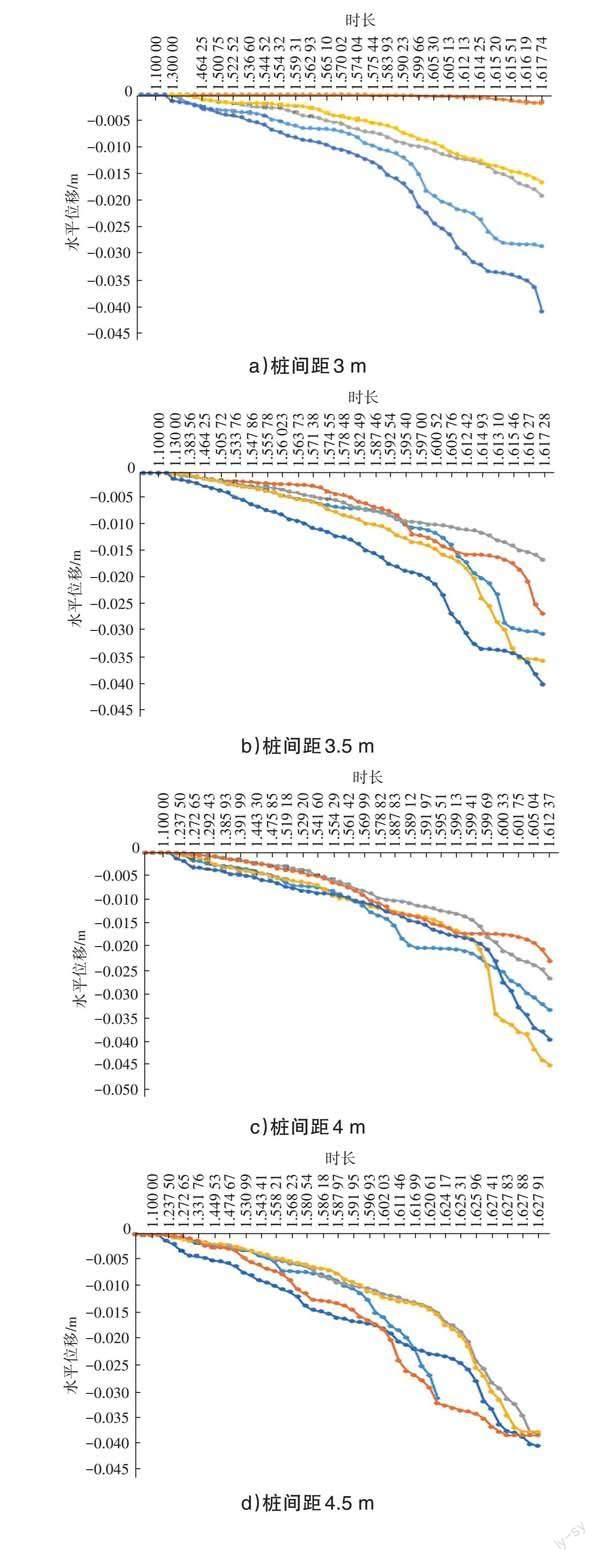
选取坡脚任一点，研究不同时间下，桩间距与桩截面对坡体水平位移影响。见图6。

坡体整体位移方向不随截面形状和桩间距发生变化，均向左。相同桩间距下，长方形截面加固效果最理想；圆形截面坡体变形较大，综合考虑施工不便等因素，工程实践中应尽量避免使用圆形抗滑桩。从正方形到圆形，截面边数逐渐增加，坡体位移逐渐变大；可近似看做截面边数与坡体加固效果负相关。

随计算时长增加，坡体位移增大；从时长1.600 00开始，位移出现较大变化且随桩间距增加，位移突变出现时间逐渐提前。不同截面形状抗滑桩对桩间距变化的敏感度不同，正方形和长方形截面在桩间距＞4 m后位移变化较小；正六边形截面抗滑桩在桩间距＞4.5 m后位移基本不变，与由安全系数和接触应力得到的不同截面形状抗滑桩最优桩间距基本相同。

2.4 相同安全系数下抗滑桩内力及位移分布规律

为研究不同截面抗滑桩两侧内力随安全系数变化规律，分别提取单抗滑桩在折减系数分别为1.25、1.45时桩的接触应力和水平剪力（当桩间距为无限远时，桩间影响较小，可近似作为单桩处理）。见图7-图10。

相同折减系数，截面形状对桩身内力分布几乎没有影响，这是由于桩长、岩体一定情况下，岩体作用于抗滑桩的接触力不变，故在不考虑桩的微变形情况下，桩身内力分布情况也是一定的；相同桩身，折减系数越高，应力越集中，桩后应力集中程度越强。随着边数增多，截面越趋近于圆形，此时应力呈圆弧状。

折减系数1.25，随着截面边数增多，抗滑桩位移在一定程度上有逐渐减小的趋势且方形截面整体变形幅度较大，这是由于方形较圆形抗滑桩更容易出现应力集中，从而对桩体产生幅度较大的变形，与实际情况相符。见图11。

当折减系数从1.25增长到1.45，纵向沿着桩身的剪力峰值提高幅度超过40%；圆形截面剪力峰值提高幅度最大，为46.14%。但实际工程中，抗滑桩所能承受的剪力存在上限值，超过会发生塑性变形甚至破坏。见图12。

同抗弯刚度下，截面形状对桩水平位移方向和位移分布几乎没有影响，较大水平位移均在桩顶；矩形比圆形抗滑桩桩身位移大。见图14。

四种截面桩中，从正方形到圆形桩两侧接触应力峰值依次增大，水平剪应力依次减小，内力分布情况基本相同，桩前侧接触应力和水平剪应力较大变化均在距桩顶4～12 m位置。可近似认为，随着截面边数增多，接触应力逐渐增大，水平剪应力逐渐减小。这是由于随着截面边数增大，抗滑桩截面逐渐趋于圆形，圆形桩承受较大接触应力，承受剪力相应较小，与实际情况相同。见图15和图16。

3 结论

1）相同桩间距下，随着抗滑桩截面边数增加，安全系数逐渐降低，当边数趋近无限多时，截面趋近圆形，安全系数最小。若边坡滑动方向已知，长方形抗滑桩为最优选择；若滑动方向未知，正方形抗滑桩为最优选择。由于抗滑桩塑性变形较小，可近似看做刚性挡墙，在滑动方向已知的情况下，垂直滑动面边与平行滑动面边比值越大，墙面越宽，滑动位移越小，抗滑能力越强，安全系数越大。相同抗滑樁截面形状下，随着桩间距逐渐增大，安全系数也逐渐降低，当桩间距无限大时，相邻两桩互相影响忽略不计，可近似看做单桩作用，此时安全系数最小。

2）截面形狀为正方形和长方形时，最优桩间距近似为4 m；截面形状为正五边形和正六边形时，最优桩间距近似为4.5 m截面形状为圆形时，桩间距至少应＞5 m。由此可知：随着截面边数逐渐增大，最优桩间距有逐渐增大的趋势，但间距过分大会导致边坡稳定性下降，因此抗滑桩间距应在一定范围。

3）应力集中在桩底位置不受截面形状和桩间距影响；工程实践中，为防止应力过大底部折桩，应适当增加抗滑桩底部强度。桩间距对抗滑桩应力分布情况几乎没有影响，截面形状对抗滑桩应力分布有较明显影响；桩前和桩后随桩间距的变化趋势基本相同，但桩前接触应力近似为桩后接触应力的2倍。另外，相同桩间距下，正方形最大接触应力最大，圆形接触应力较小，间接可以说明随着截面边数增加，抗滑桩接触应力出现逐渐缩小的趋势。

4）边坡整体位移方向不随截面形状和桩间距发生变化，均向左。相同桩间距，长方形截面加固效果最理想；圆形加固变形较大，综合考虑圆形状施工不便等因素，应尽量避免使用圆形抗滑桩。抗滑桩加固边坡中，截面形状从正方形到圆形，截面边数逐渐增加，坡体位移逐渐变大；可近似看做截面边数与坡体加固效果负相关。随计算时间的增加，坡体位移增大，从计算时长1.6开始，位移均变化较大且随着桩间距在一定范围内的变化，位移突变情况出现时间逐渐提前。

5）相同折减系数下，不同截面形状对桩身内力分布几乎没有影响，在不考虑桩的微变形情况下，桩身内力分布情况是一定的。在相同桩身处，抗滑桩安全系数越高，应力越集中，桩后应力集中程度越强。随着边数增多，截面越趋近于圆形，此时应力呈圆弧状。此外，随着截面边数增多，抗滑桩位移在一定程度上有逐渐减小趋势且方形抗滑桩整体变形幅度较大；这是由于方形抗滑桩较圆形桩容应力更易集中。纵向沿桩身剪力峰值随折减系数增大而增大；实际工程中，抗滑桩所能承受的剪力存在上限值，当达到抗滑桩所能承受的范围时抗滑桩将会发生塑性变形甚至破坏。

6）相同抗弯刚度条件下，正方形和长方形安全系数均大于正六边形和圆形截面桩，可近似认为随着截面边数增加安全系数逐渐减小，接触应力逐渐增大，水平剪应力逐渐减小；抗滑桩截面对桩水平位移方向和位移分布几乎没有影响，不同截面桩较大水平位移均桩顶且矩形抗滑桩比圆形抗滑桩桩身位移大。

参考文献：

[1]Cai F ，Ugai K . Numerical analysis of the stability of a slope reinforced with piles[J]. Soils and Foundation，2000，40（1）：73-84.

[2]陈昌富，肖淑君.基于加权残值法和统一强度理论抗滑桩合理锚固深度的确定方法[J].工业建筑，2009，39（1）：85-89.

[3]周记名. 圆形截面抗滑群桩抗滑机理研究[D].成都：西南交通大学，2015.

[4]司光武. 矩形与圆形截面抗滑桩离心模型试验及颗粒流数值模拟研究[D]. 成都：西南交通大学，2017.

[5]朱兴帅. 不同截面抗滑桩承载性状研究[D]. 湘潭：湖南科技大学，2017.

[6]李    贤，徐则民.圆形截面抗滑桩受力分析及实验研究[J].公路交通科技（应用技术版），2018，14（2）：115-117.

[7]郑百录，冯    瑞.机械成孔圆形桩与人工挖孔矩形桩对比分析——以西南某运营高速公路路基变形处治工程为例[J].西南公路，2018，（2）：51-53.

[8]年廷凯，徐海洋，李东晨.不同截面型式抗滑桩加固边坡数值分析[J].大连理工大学学报，2013，53（5）：695-701.

[9]李    浩，殷德胜.地质条件及桩间距对桩身土压力的影响[J].人民黄河，2019，41（S2）：147-150.

[10]丁桥军，董铁斌.抗滑桩参数变化对土质边坡稳定性的影响研究[J].公路与汽运，2020，（1）：68-71.

[11]谢明星，郑俊杰，曹文昭，等.联合支挡结构中抗滑桩设计参数分析与优化[J].华中科技大学学报（自然科学版），2019，47（7）：1-7.

[12]Jinoh Won，Kwangho You，Sangseom Jeong，et al. Coupled effects in stability analysis of pile-slope systems[J]. Computers and Geotechnics，2005，32（4）：304-315.

[13]Wei W B，Cheng Y M. Strength  reduction analysis for slope  reinforced with one row of piles[J].computers and geotechnics，2009，36（7）：1176-1185.