抗滑桩加固边坡稳定性分析及优化研究
岳英龙
(烟台职业学院 建筑工程系,山东 烟台 264670)
抗滑桩作为一种有效的支挡结构,因其具有抗滑能力强、布置灵活、施工方便等特点,在边坡工程中得到广泛应用。以往针对抗滑桩的理论分析主要是通过建立相应的数学或物理模型,研究土体侧向移动对抗滑桩的影响[1-2]。常用的极限平衡法需要对桩体受力形式及边坡滑动面进行假设,无法全面反映抗滑桩—边坡的耦合效应以及边坡的滑移特征[3-4]。近年来,随着计算机技术的不断发展,数值分析方法特别是基于强度折减技术的有限元法或有限差分法[5-6]给抗滑桩加固边坡的数值模拟提供了新的手段。文献[7]利用极限平衡法和有限差分软件 FLAC3D分析边坡稳定性,并从边坡稳定系数和抗滑桩的力学响应2方面加以比较。文献[8]利用 FLAC3D软件,分析了含抗滑桩的边坡稳定性优化问题。然而,在抗滑桩数值分析中,仍有2个重要问题有待解决:抗滑桩加固位置对桩身的内力、变位以及边坡滑移面的影响;抗滑桩弹性模量的选取。目前,在抗滑桩工程的优化模拟中,对于桩长的优化较多,而对于抗滑桩加固位置的优化,常以边坡的稳定系数作为唯一的优化指标,没有考虑抗滑桩在不同加固位置时桩身的内力、变位响应以及边坡滑移面的变化趋势。此外,以往的数值模拟通常是考虑单个因素进行分析,没有考虑抗滑桩因素间的相互作用,由此得出的结果可能存在一定偏差。在钢筋混凝土抗滑桩工程中,对桩体弹性模量的研究较少,对其取值的规定也不够严格,常根据工程经验确定。抗滑桩的弹性模量对边坡稳定性、自身内力及变位有何影响,尚待研究。
本文结合考虑桩—土相互作用的强度折减法,对抗滑桩加固边坡进行数值分析,研究抗滑桩的布设位置、桩长、弹性模量等因素对边坡整体稳定系数的影响,分析在各种工况下抗滑桩内力、桩身变位特点,以期为抗滑桩工程设计提供参考。
1 抗滑桩加固作用的数值建模
在FLAC3D软件中,可采用实体单元和桩单元[9-10]这2种方法模拟抗滑桩。本文采用桩单元模拟抗滑桩。桩单元与实体模型网格之间的相互作用(桩—土相互作用)通过法向和切向的耦合弹簧实现。耦合弹簧为非线性弹簧—滑块连接体,它们能够在桩单元节点处实现桩单元与实体单元网格间力和弯矩的传递,如图1所示。
1.1 剪切连接弹簧的力学特性
桩和网格的交界面的剪切强度由在桩的端节点处的弹簧—滑块系统表示。在桩节点和围岩网格之间的相对位移而产生的剪切力为:
(1)
式中,Fs为连接弹簧产生的剪切力;csstiff为连接弹簧承受的剪切刚度;usi为抗滑桩的轴向位移;usm为介质岩土面的轴向位移;L为桩的单元长度。

图1 抗滑桩力学模型Fig.1 Mechanical model of anti-slide pile
1.2 法向连接弹簧的力学特性
抗滑桩连接弹簧的法向力求解:
(2)
式中,Fn为耦合弹簧产生的法向力;cnstiff为耦合弹簧承受的法向刚度;uni为垂直于桩轴向方向桩的位移;unm为垂直桩轴方向上的介质面位移;L为桩单元的有效长度。
2 数值模型
设置某边坡的高度为20 m,坡度比为1∶1,依据平面应变原理建立相应的计算模型,建模时需考虑边界条件的影响;同时在边坡的临坡面处设置加密网格措施,提高模型计算的精度。模型共设置6 216个节点,共计4 410个单元,如图2所示。初始应力场按照自重应力场予以考虑,土体相关参数见表1。设定边界约束条件为下部固定约束,边坡左右两侧为法向约束,边坡上部设定为自由边界。相关测试土体采用能兼顾关联流动拉伸屈服和非关联流动剪切屈服的Mohr-Coulomb法则[11]进行计算。模型计算的收敛准则采用不平衡力比率为10-5内[11]。采用强度折减法计算边坡整体稳定系数,以计算是否收敛作为边坡失稳判据[12]。当边坡达到临界失稳状态时,必然是一部分岩土体相对于另一部分发生无限制的滑移,于是边坡体被明显地分为滑体和稳定体 2 部分,可将这2部分之间的分界线定义为滑动面。利用自编FISH语言将该曲线和边坡线数据取出,从而量化滑动面上各点的位置。

图2 数值模型Fig.2 Numerical model

表1 边坡的物理力学参数Tab.1 Physical and mechanical parameters of slope
3 抗滑桩布置方案
初始计算结果显示,临界滑移面剪出口位置在坡脚以上。若抗滑桩布置在坡脚,则抗滑桩不会穿过滑移面,达不到加固效果,故无需在坡脚布桩。具体位置是:抗滑桩加固位置水平投影到坡脚距离Lx从2.5 m变化到20.0 m,步长为 2.5 m。边坡水平投影长度L=20.0 m,Lx/L=1/(8.0~1.0)。以下简称这 8个设桩位置分别为L1—L8。滑体厚度最小值出现在L1处,为4.6 m。因此,取最小桩长为6.0 m,增幅为2.0 m。抗滑桩截面形式为矩形,桩宽b=1.0 m,高h=1.5 m。抗滑桩布置如图3所示,物理力学参数见表2。
4 抗滑桩优化分析
4.1 桩位置和桩长对边坡稳定性的影响
(1)抗滑桩加固位置对边坡稳定性的影响。从图4可知,当在坡顶或坡脚处设桩时,边坡稳定系数略比无桩状态时高。在桩长较小时,相同桩长对应的稳定系数较接近,说明在桩长较小时,抗滑桩加固位置对边坡稳定性的影响较小。当桩长超过16 m时,抗滑桩加固位置的影响明显增大:桩长为16~20 m 时,L4曲线(边坡中部位置)对应的稳定系数最大;当桩长超过20 m时,最优设桩位置不再是边坡中部,而是在L5位置,说明最优设桩位置与抗滑桩嵌固深度有关。因此,在抗滑桩工程设计中,当桩长较长时,将抗滑桩布设位置从边坡中部往坡顶偏移一定距离(本工程为L/8),抗滑桩加固效果将更显著。

图3 抗滑桩的布置示意Fig.3 Layout of anti-slide piles

表2 物理力学参数Tab.2 Physical and mechanical parameters
(2)抗滑桩桩长对边坡稳定性的影响。从图4可看出,抗滑桩越长,稳定系数越高,即边坡越安全,但达到一定长度后,抗滑桩长度增加起不到明显的效果。这说明在抗滑桩加固边坡工程中,存在一有效嵌固深度H,且H受到设桩位置的影响;在L5位置有最大的嵌固深度,见表3。此外,从图4还可看出,在有效桩长内的稳定系数和桩长的关系都近似于抛物线。

图4 抗滑桩加固位置、桩长对边坡稳定系数的影响Fig.4 Influence of anti slide pile reinforcement position and pile length on slope stability coefficient

表3 抗滑桩加固位置对其有效嵌固深度的影响Tab.3 Influence of anti-slide pile reinforcement position on its effective embedded depth
4.2 桩位置和桩长对边坡临界滑移面的影响
在边坡上的设桩位置不同,边坡的临界滑移面也不同,如图5所示。随着抗滑桩位置往坡顶靠近,剪出口位置也往坡顶移动,临界滑移面逐渐往边坡临坡面移动,破坏模式由深层滑动逐渐变为浅层滑动;抗滑桩位置在L1和L2时,边坡临界滑移面位置基本一致,在L2到L5位置之间,相同的抗滑桩位置增量(Lx=2.5 m)引起的滑移面位置的变化较大,且剪出口位置的变化量大致相等;当抗滑桩加固位置在L6时,边坡滑移面的变化趋势发生了突变,剪出口位置突变到坡脚以外,临界滑移面也不再近似为圆弧形。
固定抗滑桩位置于L5,改变抗滑桩桩长,得到桩长对边坡临界滑移面的影响如图6所示。

图5 桩位置对边坡临界滑移面的影响Fig.5 Influence of pile position on critical slip surface of slope
从图6可看出,随着桩长增大,滑移面逐渐向边坡内部移动,破坏模式由浅层滑动变为深层滑动;当桩长超过24 m时,边坡的临界滑移面位置发生突变,迅速靠近坡面,剪出口位于抗滑桩顶部,由原先的深层滑移转变为浅层滑移。这是由于抗滑桩加入土体后,桩与土体形成复合结构,提高了土体的抗滑能力。边坡的滑移面逐渐往坡内移动;但当桩长达到一定程度时,复合体的范围较大,此时向坡内移动的滑移面稳定系数大于临坡面的滑移面稳定系数,从而使边坡的滑移面转移到临坡面位置。
4.3 桩位置和桩长对桩身内力和变位的影响
沿抗滑桩的剪力分布如图7所示,沿抗滑桩的变位曲线如图8所示。从图7、图8可看出,随着抗滑桩加固位置向坡顶移动,桩身最大剪力先增大后减小,最大值都出现在L3处。这是因为抗滑桩设置在L1和L2位置时,相应的临界滑移面基本不通过抗滑桩;在L4位置及之后,滑移面向临坡面靠近,滑坡体体积减小,这都使得抗滑桩受到的滑坡推力减小,因此,抗滑桩布设在L3处时,剪力最大。经计算,最大剪力是L5处的3.9倍。可见,若将抗滑桩布设在L3位置,需要更大的桩身截面或布置更多的受力钢筋。此外,在L6及之后位置,抗滑桩的桩身剪力均近似相等,说明越靠近坡顶,抗滑桩布设位置对抗滑桩内力影响越小。从图8可知,随着抗滑桩加固位置向坡顶移动,桩顶挠度先增大后减小,在L3处达到峰值;在L6及之后位置,桩顶挠度很小,仅为19.2 mm;另外,在L7、L8位置,桩身的变位曲线近似为直线,说明抗滑桩产生转动,可能发生倾覆破坏。这是由于抗滑桩布设在L7、L8位置时,边坡滑体厚度较大(图5),因而抗滑桩嵌固深度较小,锚固不足。

图8 不同桩位置沿抗滑桩的变位曲线Fig.8 Displacement curve diagram along the anti-slide pile
另外,布置抗滑桩在L5处,不同桩长工况下的抗滑桩内力、变位响应如图9、图10所示。从图9可知,随着桩长增加,桩身剪力随桩长的变化并不明显,最大剪力只有最小剪力的1.4倍,最大剪力点不随桩长改变,保持在距离桩顶7 m左右的位置。从图10可知,随着桩长的增加,桩顶挠度逐渐减小,对于相同的桩长变化量H,桩顶挠度减小的幅度不断变小;当桩长超过16 m时,继续增加桩长,桩顶挠度不再变化;当抗滑桩桩长只有10 m时,桩顶挠度达955 mm,这与边坡原始状态的最大水平位移相近,且变位曲线近似为直线,说明抗滑桩发生转动而不是弯曲。这是因为抗滑桩过短,嵌固深度不足,可能产生倾覆破坏。

图9 不同桩长工况下沿抗滑桩的剪力分布Fig.9 Shear force distribution diagram along the anti-slide pile
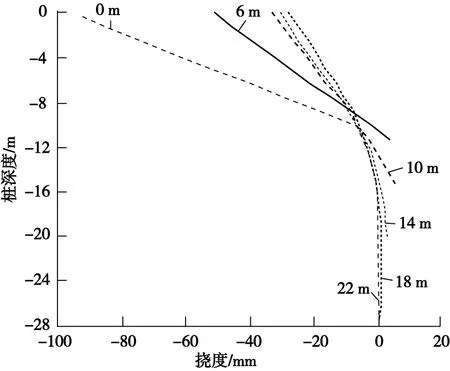
图10 不同桩长工况下沿抗滑桩的变位曲线Fig.10 Displacement curve diagram along the anti-slide pile
4.4 抗滑桩弹性模量对边坡稳定性影响
固定抗滑桩位置于L5,仅调整抗滑桩弹性模量进行分析。抗滑桩弹性模量对边坡稳定系数的影响见表4。从表4可知,随着弹性模量增加,稳定系数增加较小,近似认为抗滑桩弹性模量对边坡稳定系数无影响。

表4 抗滑桩弹性模量对边坡稳定系数的影响Tab.4 Influence of anti-slide pile elastic modulus on slope stability coefficient
4.5 抗滑桩弹性模量对桩身内力和变位的影响
沿抗滑桩的剪力分布如图11所示。不同弹性模量下沿抗滑桩的变位曲线如图12所示。从图11 可知,随着桩身弹性模量的增加,桩身剪力增大,其变位减小。原因在于随着抗滑桩弹性模量的增大,抗滑桩刚度相应增大,在桩—土体共同作用下,抗滑桩承受的内力也相应增大,而桩身内力、桩顶挠度变化幅度均十分有限,桩顶挠度相差为3.4 mm。综合边坡稳定系数和抗滑桩内力、变位分析,提高抗滑桩弹性模量减小桩体变位,但不能提高边坡的稳定性,且提高桩体弹性模量会采用更高强度等级的混凝土或受力钢筋,将提高抗滑桩造价。因此,在抗滑桩设计中,应合理确定抗滑桩弹性模量。

图11 不同弹性模量下沿抗滑桩的剪力分布Fig.11 Shear force distribution diagram along the anti-slide pile
5 结论
利用本文所提的数值方法分析了抗滑桩在边坡加固的工程应用效果,得出了设桩位置、桩长、弹性模量等因素对边坡稳定性、桩体受力及变位的影响,结论如下。

图12 不同弹性模量下沿抗滑桩的变位曲线Fig.12 Displacement curve diagram along the anti-slide pile
(1)抗滑桩加固位置对于边坡稳定系数的影响程度同桩长有关。当桩长较小时,抗滑桩加固位置的变化对于边坡稳定性的影响很小;反之,影响显著增强。同时,抗滑桩设桩最优位置也受其影响。若桩长较短,则布设抗滑桩于边坡中部具有最好的加固效果;反之,在边坡中上部设桩对边坡稳定性更好。
(2)抗滑桩加固位置往坡顶靠近,桩身内力、桩体变位先增大后减小,并在边坡中下部同一位置同时达到最大。
(3)抗滑桩桩长增大,桩体剪力变化很小。对于桩顶自由约束的抗滑桩,若嵌固深度不足,则抗滑桩可能发生倾覆破坏。在抗滑桩加固边坡工程中,存在一有效嵌固深度H:当桩长超过H时,继续增大桩长并不能提高边坡的稳定系数;在有效嵌固深度内,边坡稳定系数和桩长的关系符合抛物线特征。
(4)提高抗滑桩弹性模量可减小桩体变位,但不能提高边坡稳定系数,同时,提高抗滑桩弹性模量会提高造价。因此,在抗滑桩工程设计中,应合理确定桩身弹性模量。

