孔洞特征模型特征分割及自适应分层算法

潘科峰，孔令旺，赵刚

（1.青田县职业技术学校 智能制造学部，浙江 丽水 323900；2.吉林工程职业学院 信息工程学院，吉林 四平 136000；3.吉林大学，长春 130021）

近年来，3D 打印技术已经成为智能制造领域的研究热点。3D 打印技术本质上采用了离散堆叠的思想，离散过程是指通过计算机对三维数据模型进行分层，获得一系列的二维平面轮廓。堆叠是指使用打印耗材逐层填入模型二维平面轮廓内，完成整个模型的实体制造过程[1-2]。由于3D 打印逐层叠加的制造原理，模型表面会出现“阶梯”状层纹，当层厚较大时，阶梯效应较为明显，模型的成形质量较差[3-4]。为了提升熔融沉积成形3D 打印的制件质量，减小阶梯效应对模型精度的影响，一般采用减小分层厚度的方式，但是该方式会增加模型成形耗时，因此传统等厚分层不能很好地解决成形质量和打印耗时之间的矛盾。自适应分层能够根据模型的轮廓特点自行调整分层的层厚，在一定程度上能够提升制件的成形质量，减少打印耗时。传统等厚分层和自适应分层均采用整体式分层的策略，对于孔洞特征模型，通过调整模型整体分层层厚来平衡成形质量和打印耗时的效果较差。

模型分割能够根据模型特征将模型分成不同部分，再对不同部分的模型进行分层处理，进而提升模型的成形质量。Wang 等[5]基于视觉显著性的分割方法，通过水平和垂直分割平面，将模型分为多个段块，然后对每个分割段进行了自适应分层处理。王春香等[6]同样采用模型分割原理先完成了模型的凸起特征分割，再分别进行自适应分层，但该方法为人工分割，对复杂模型不太适用。Kristian 等[7]运用聚类的方法找到多组分割交点和分割法线，通过正交法线和分割中心实现模型分割，并对分割后的模型进行边缘体素化，通过计算模型的体积损失误差，找到误差最小的方向，对模型进行等厚分层处理，该方法的模型体素化过程会降低算法处理效率。根据层厚判据及侧重点的不同，自适应分层算法的效果有所区别。林琼洁等[8]、田仁强等[9]和Wang 等[10]通过STL 模型三角面片法向量与成形方向的夹角实现了自适应调节层厚，有效提升了模型成形质量，但成形时间较长。LYU 等[11]提出了一种基于体积误差最小原则，寻找最优三角面片法矢量与成形方向的夹角来实现自适应分层的方法。Pan 等[12]通过比较两分层轮廓的面积变化情况，确定了下一层分层厚度，但由于模型形状多变，成形精度较差。魏效玲等[13]和周惠群等[14]利用模型外轮廓曲线切线与打印方向夹角实现了自适应分层，但其算法处理过程较为复杂。王军伟等[15]、韩江等[16]、Navangul 等[17]、朱敏等[18]主要考虑了模型特征丢失及偏移问题，通过改进分层算法，有效识别和保留了模型的微小细节特征，但缺乏考虑阶梯效应对模型的影响。

针对目前整体式分层算法对孔洞特征模型分层不能较好协调成形精度和打印耗时之间关系的问题，本文提出了一种孔洞特征模型特征分割及自适应分层算法，并给出了针对STL 模型孔洞特征分割位置的判定方法，以及对分割后模型自适应分层处理的具体过程。

1 孔洞特征模型分割

1.1 STL 文件读取

STL 模型文件采用以大量三角面片拟合轮廓的方式表达模型几何特征，文件中主要包含三角面片的顶点坐标数据和三角面片的法向矢量，具有格式简单、易读取等优点，是目前最常用的3D 打印模型文件[19-21]。STL 模型文件有2 种数据格式：文本格式（ASCII）和二进制格式（Binary）[22]。本文通过MATLAB 平台读入二进制格式的STL 模型，由于螺母模型内部螺纹以及拇指轮模型的外侧滚花在实际制造过程中要求较高，因此使用如图1 所示的螺母模型和拇指轮模型算法进行验证。

1.2 阶梯效应与衡量参数

完成STL 模型读入后，要进行分层处理。分层处理通常以一系列分层平面求取STL 模型的每一层截面轮廓曲线，然后偏移轮廓曲线，计算出模型外壳打印路径，并对模型进行填充及路径规划，最后输出数控程序指令G-code，3D 打印机按照G-code 完成模型实体制造[23-24]。

分层获取模型每一层的二维平面轮廓，在打印过程中，熔融耗材按照层厚高度填充模型轮廓，如果上下两层的轮廓不相同，势必会造成打印的模型实体与STL 模型存在一定偏差，即阶梯效应，如图2 所示。其中z为成形方向，D、d为层厚，T为模型表面，α为模型在该处轮廓切平面的法向矢量与成形方向z的夹角，ΔVi是第i层实体与STL 模型的几何误差。当分层厚度为D时，模型分层层数较少，成形效率较高，几何误差ΔVi较大，即阶梯误差较大；反之，当分层厚度为d时，模型分层层数增加，成形效率降低，几何误差ΔVi减小。同时，α随着模型曲率发生变化，在相同层厚下，当α较小时，几何误差ΔVi较大；反之，当α较大时，几何误差ΔVi较小。

图2 STL 模型阶梯效应示意Fig.2 Schematic diagram of the step effect of the STL model:a) large thickness slicing; b) small thickness slicing

自适应分层能在模型曲率变化大区域，即当α较小时，自动减小层厚，进而达到减小几何误差ΔVi和降低打印耗时的目的。在实际分层应用中，通过ΔVi来衡量几何误差的计算过程较为复杂，因此，有学者提出通过阶梯高度来衡量模型的几何误差。相邻分层平面的Zi和Zi+1分层示意图如图3所示。其中，αj为模型在该处三角面的法相矢量与分层方向z的夹角，夹角的计算如式（1）所示；di+1是第i+1 层的分层厚度，δi为阶梯高度，即该层模型实体与模型表面T的最大距离[25]。

图3 分层几何误差示意Fig.3 Schematic diagram of sliced geometric errors

由图3 可以建立di+1、δi、αj三者之间的关系，如式（2）所示。

由式（2）可知，当αj不变时，层厚di+1减小，阶梯高度δi减小，模型精度提升；当层厚di+1无限小时，阶梯高度δi无限趋近于0，模型成形实体与STL模型一致。受限于打印机制造工艺，分层厚度不可能无限制减小，因此，模型分层厚度介于设置的最大分层厚度和最小分层厚度之间，当层厚在这个区间内时，可以通过设置期望阶梯高度δi、计算模型层厚（依据式（2）），来保证模型的成形精度。模型与单个分层平面交有多个三角面片，并且这些三角面片的法向矢量不尽相同，为了保证计算出的层厚能够符合该层相交的所有三角面片，式（2）中αj采用的是同一分层平面相交的三角面片中法向矢量与z轴夹角的最小值，同时为了衡量模型整体打印质量，计算每层分层平面相交三角面片的阶梯高度均值，再对所有层的阶梯高度求均值，如式（3）所示。

式中：k为当前层相交三角面片数；δi为根据式（2）计算得到的第j个三角面片的阶梯高度；n为分层层数；为整体模型的平均阶梯高度。

2 自适应分层算法

2.1 孔洞特征分离

采用与当前层相交三角面片的法向矢量与z轴相交的夹角最小值进行自适应分层的层厚计算。对于孔洞模型，整体式分层同一层相交三角面片分别包含孔洞特征三角面片和其他部分三角面片，显然采用整体式获取的层厚能够满足设置的期望阶梯高度，但是这会增加一部分模型的分层层数，降低了打印效率。如果将孔洞特征模型分成孔洞特征部分和其他部分，分别进行自适应分层，可将影响层厚计算的三角面片范围缩小到局部区域所包含的三角面片，分层的层厚更贴合模型特征。模型中处于水平的三角面片在分层过程中无法与分层平面相交，因此，可以通过剔除模型底部和上部水平三角面片的方式，使孔洞特征部分的三角面片与其他区域的三角面片处于非邻接状态，然后通过拓扑搜索将两部分模型所包含的三角面片分离[26]，分离结果如图4 所示。

图4 孔洞特征分离Fig.4 Hole feature separation

2.2 三角面片法向量分层算法

在本文的分层算法中，通过式（2）计算不同大小法向量夹角对应的层厚，设置的期望阶梯高度值为0.05 mm，最小层厚为0.02 mm，最大层厚为0.3 mm。在层厚允许区间内，角度α-分层厚度d的变化曲线如图5 所示。将计算获得的不同高度分层平面分别与螺母模型分离出的两部分三角面片求交线段，获得分层轮廓，然后进行轮廓偏移求出壳体的打印路径，螺母模型孔洞特征和其他部分自适应的分层模拟图如图6所示。按照完整模型以等厚分层方法计算获得模型的填充区域并生成支撑，最后将壳体、填充和支撑等部分的打印路径整合在一起，输出完整的模型打印G-code。

图5 法向矢量夹角与层厚关系Fig.5 Normal vector angle vs. layer thickness

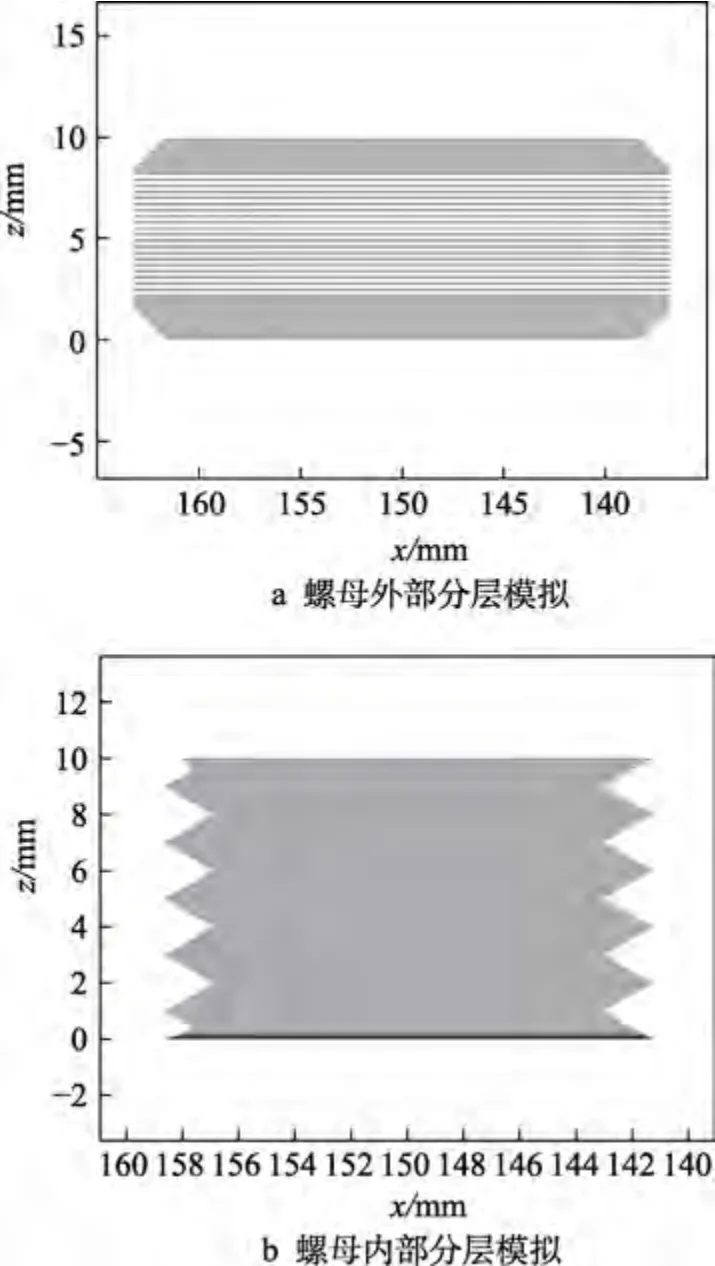
图6 模型各部分自适应分层模拟Fig.6 Adaptive slicing simulation for all parts of the model:a) simulation of the outer layering of the nut;b) simulation of the internal layering of the nut

2.3 分层算法流程

由于在自适应分层处理过程中，根据式（2）计算的是下一层的厚度，因此，需要人为设置第一层分层厚度，并且从第二层分层开始为自适应分层，本文分层算法流程如图7 所示。

图7 本文分层算法流程Fig.7 Slicing algorithm process in this paper

1）步骤1：读取二进制格式的STL 模型文件，设置分层厚度范围为最小层厚dmin至最大层厚dmax，然后根据式（1）计算所每个三角面片法向矢量与z轴的夹角α，并将模型上下底的水平三角面片剔除，对剩余三角面片建立拓扑结构。

2）步骤2：以任意模型孔洞特征包含的一个三角面片tir1为起始，根据建立的拓扑结构，遍历所有三角面片，这样将可以通过tir1拓扑搜索得到的三角面片信息存入 facet1中，不能拓扑搜索到的存入facet2中。

3）步骤3：求出facet1、facet2与层高zi、zj相交的三角面片，分别查询其中的最小夹角αi、αj，然后根据式（2）计算出层厚dlayer1、dlayer2，判断计算的层厚是否在设置层厚范围内，若是小于最小层厚，则下一层层高为上一层层高加上dmin；若大于最大层厚，则下一层层高为上一层层高加上dmax；若在层厚范围内，则下一层层高为上一层层高加上dlayer1或dlayer2。

4）步骤4：判断当前层高是否大于zmax，若分层高度大于zmax则分层结束，并将两部分分层轮廓线整合为一体，否则返回步骤3。

3 分层模拟及实验性打印

3.1 分层模拟

本文使用的2 个示例模型的3 种分层算法分层模拟图如图8 所示。3 种分层算法分别是等厚分层算法、文献[9]所提三角面片法向量自适应分层算法及本文所提分层算法，其中等厚分层算法得到的层厚为0.3 mm。从图8 可以看出，文献[9]实现了整体式自适应分层，本文分层算法实现了孔洞内外特征单独自适应分层。

图8 3 种分层算法分层模拟对比Fig.8 Slicing simulation comparison of 3 slicing algorithms: a) uniform slicing of the nut model; b) nut model literature [9] slicing; c) the nut model sliced in this article; d) uniform slicing of the thumb wheel model; e) thumb wheel model literature [9]slicing; f) the thumb wheel model sliced in this article

3.2 模型实体打印

为了验证本文分层算法的实际打印效果是否符合上述分层模拟结果，将2 个示例模型分别以等厚分层算法、文献[9]所提三角面片法向量自适应分层算法及本文所提分层算法输出的G-code 导入桌面级FDM打印机中完成实体制造，打印耗材使用PLA 线材，填充密度设置为30%。2 个示例模型3 种分层算法的实际打印图像如图9 所示。对于螺母模型，等厚分层实体打印模型内部的螺纹牙型未成形，文献[9]分层算法和本文分层算法模型内部的牙型成形较好。对于拇指轮模型，等厚分层算法模型外部的滚花成形较为粗糙，文献[9]分层算法和本文分层算法模型外部的滚花成形较为清晰。

图9 3 种分层算法实物打印对比对比Fig.9 Comparison of 3 slicing algorithms for physical printing: a) uniform slicing of the nut model; b) nut model literature [9] slicing; c) the nut model sliced in this article; d) uniform slicing of the thumb wheel model;e) thumb wheel model literature [9] slicing; f) the thumb wheel model sliced in this article

在示例模型打印过程中，记录了示例模型的各分层算法打印耗时，并通过式（3）计算了模型在不同算法中的平均阶梯高度值，如表2 所示。可以看出，当等厚分层的层厚为0.02 mm 时，模型成形质量最好，打印耗时最长；当分层厚度为0.3 mm 时，成形质量最差，打印耗时最少。文献[9]自适应分层算法和本文算法的成形精度和成形时间均处于等厚分层算法中2 种层厚数据之间，但是与文献[9]自适应分层算法相比，本文分层算法的精度分别提升了20.18%和62.68%，打印耗时分别缩短了34 min 和11 min。

表2 3 种分层算法实际打印数据Tab.2 Actually printed data of 3 slicing algorithms

4 结论

针对整体式分层算法对孔洞特征模型分层的层厚不够合理及成形时间较长等问题，提出了一种孔洞特征模型特征分割及自适应分层算法。本文自适应分层算法充分考虑到阶梯效应对模型精度的影响，采用先分割模型孔洞特征，再分别对各部分自适应分层的策略，实现了分层层厚更加贴合模型特征的目的，能够较好地平衡成形精度和成形效率之间的关系。