开采沉陷中GPS高程拟合代替四等水准测量方法研究
张晓东
(山西三元福达煤业有限公司,山西 长治 046000)
为保障煤矿安全生产,解决好建筑物下、铁路下和水体下压煤开采问题,《煤矿测量规程》要求,首采面及重要建构筑物必须建立地表移动观测站或专门观测站,观测站的高程精度须达到四等水准以上精度要求。目前,按进行观测站的形变监测时所使用的仪器可划分为传统手段和新技术。其中,传统手段主要包括:水准、全站仪和GPS等,新技术主要包括机载LiDAR、InSAR等[1]。由于目前规范中尚未规定新技术应用于地表移动观测站监测时的具体要求,因此在应用新技术时也会建立观测站进行验证。但是,传统的水准测量和三角高程测量适用于平原和植被不茂密的山区,且效率低、工作强度大;对于植被茂密的山区一般采用GPS观测,GPS数据处理时多应用卡尔曼滤波、神经网络等数学模型,这些方法处理的均为某一点的多次GPS数据,且要求数据量大。然而,对于单一工作面观测而言,视工作面长度的不同,一般仅需观测8~16期,同一观测站的观测次数少,从而导致误差分布不一定符合正态分布,使得使用常规GPS 数据处理方法时适用性差。因此,针对山区煤炭开采沉陷监测时,应用GPS高程拟合代替四等水准测量的方法研究成为亟待解决的问题。
目前,制约着GPS代替四等水准测量主要有两个:一是GPS测量的是大地高,水准测量的是正常高,两者间存在高程异常差值;二是GPS本身的高程观测精度低于四等水准。针对这两个主要问题,本文提出了基于观测线地形拐点的高程异常拟合方法和基于下沉曲线的GPS数据处理方法,实现了在山区开采沉陷中采用GPS高程拟合代替常规四等水准测量。
1 项目概况
研究案例位于山西省长治市武乡县,工作面走向长度1 200 m,倾向长度220 m,煤层倾角12°,平均煤厚3.2 m。工作面上方为中低山岭,沟谷发育,有2条“V”字型冲沟与工作面斜交,坡度较大,最大高差可达190 m,且植被茂密,灌木丛生,现场如图1所示。

图1 现场影像Fig.1 On-site images
为研究山区高程异常分布规律,同时验证GPS处理精度,在工作面上方布设了1条倾向观测线和半条走向观测线,相邻地表移动观测站间距约为25 m。其中,首次和末次观测时同时采用三角高程和GPS进行观测,中间8期数据仅采用GPS进行测量。根据相关规范、文献和现场监测成果,在山区采用三角高程可达到四等水准的同等精度[2]。
2 基于地形拐点的高程异常拟合
目前,常用的高程异常拟合方法主要有重力法和解析法两种,其中采用重力法拟合精度较低[3],解析法是应用多面函数、多项式等数学模型拟合高程异常的空间分布,因而对已知点的分布要求较高,而地表移动观测站一般沿走向和倾向主断面布置成“十”或“T”型[4],因此将观测点作为已知点进行全区域拟合是不合理的。针对这一问题,本文提出了一种基于观测线地形拐点的高程异常拟合方法。
2.1 观测线上高程异常分布规律
地表移动观测站一般布设在主断面上,虽然实际布设时考虑到地形等影响可能略有偏差,但总体呈现为直线或近似直线形状,因此可将高程异常拟合问题从曲面拟合简化为曲线拟合,图2和图3分别给出了走向和倾向观测线上高程异常与地形的无因次曲线。
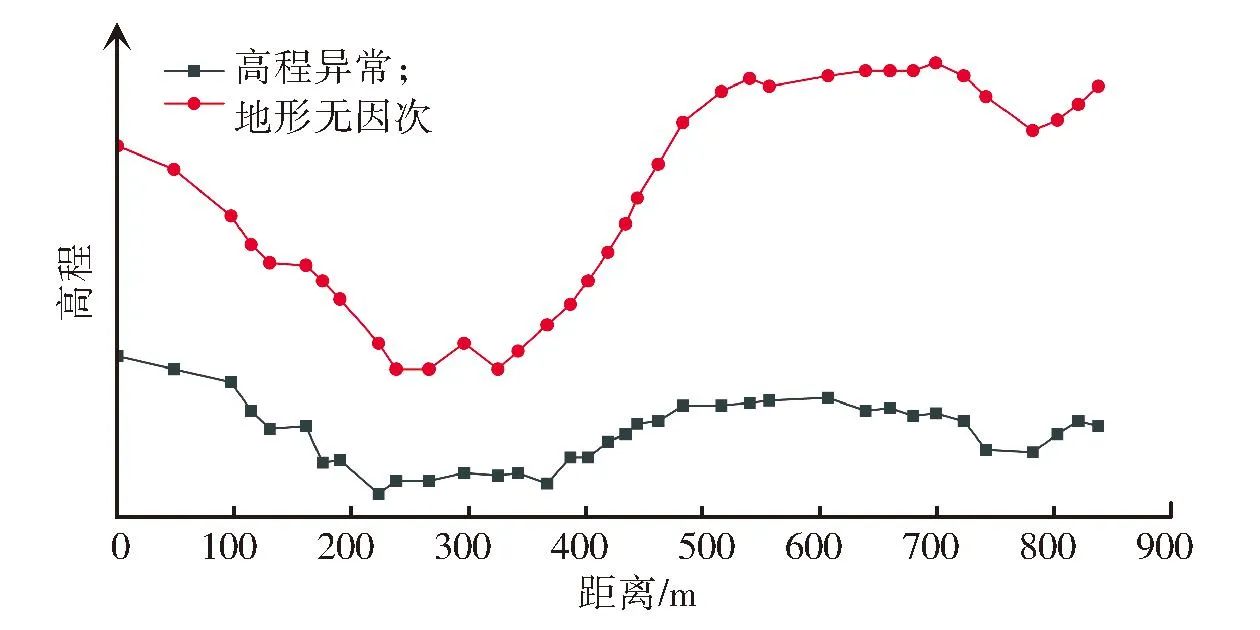
图2 走向观测线高程异常与地形的无因次曲线Fig.2 Elevation anomaly and terrain dimentionless curves toward observation line
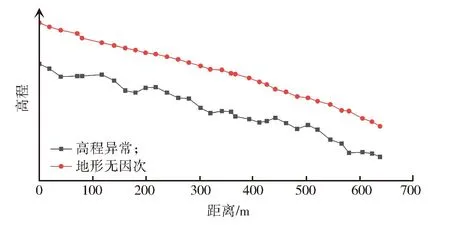
图3 倾向观测线高程异常与地形的无因次曲线Fig.3 Elevation anomaly and terrain dimentionless curves leaning to observation line
从图中可看出:①高程异常随地形的变化而变化,整体上具有正相关性;②高程异常的拐点一般出现在地形的拐点位置,但地形的拐点并不全是高程异常的拐点;③在直线型高程异常拟合时,选取地形拐点作为高程异常拟合的关键点更合理。
由于倾向观测线高程异常分布较为简单,以下仅对走向观测线高程异常进行拟合。结合地形起伏情况,选取观测线起点、终点和中间5个地形拐点作为已知点,分别采用三次样条曲线和多项式曲线拟合整条观测线的高程异常曲线,其余点用于拟合精度的检核。
2.2 三次样条拟合
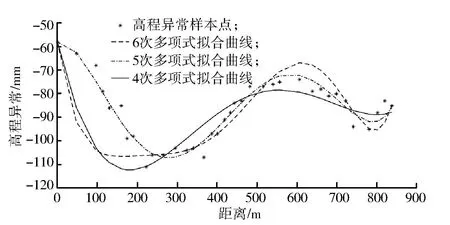
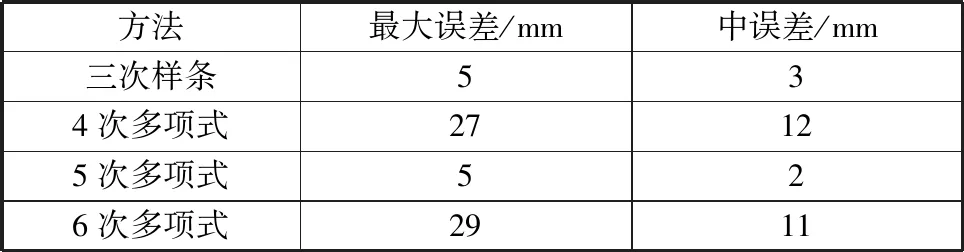
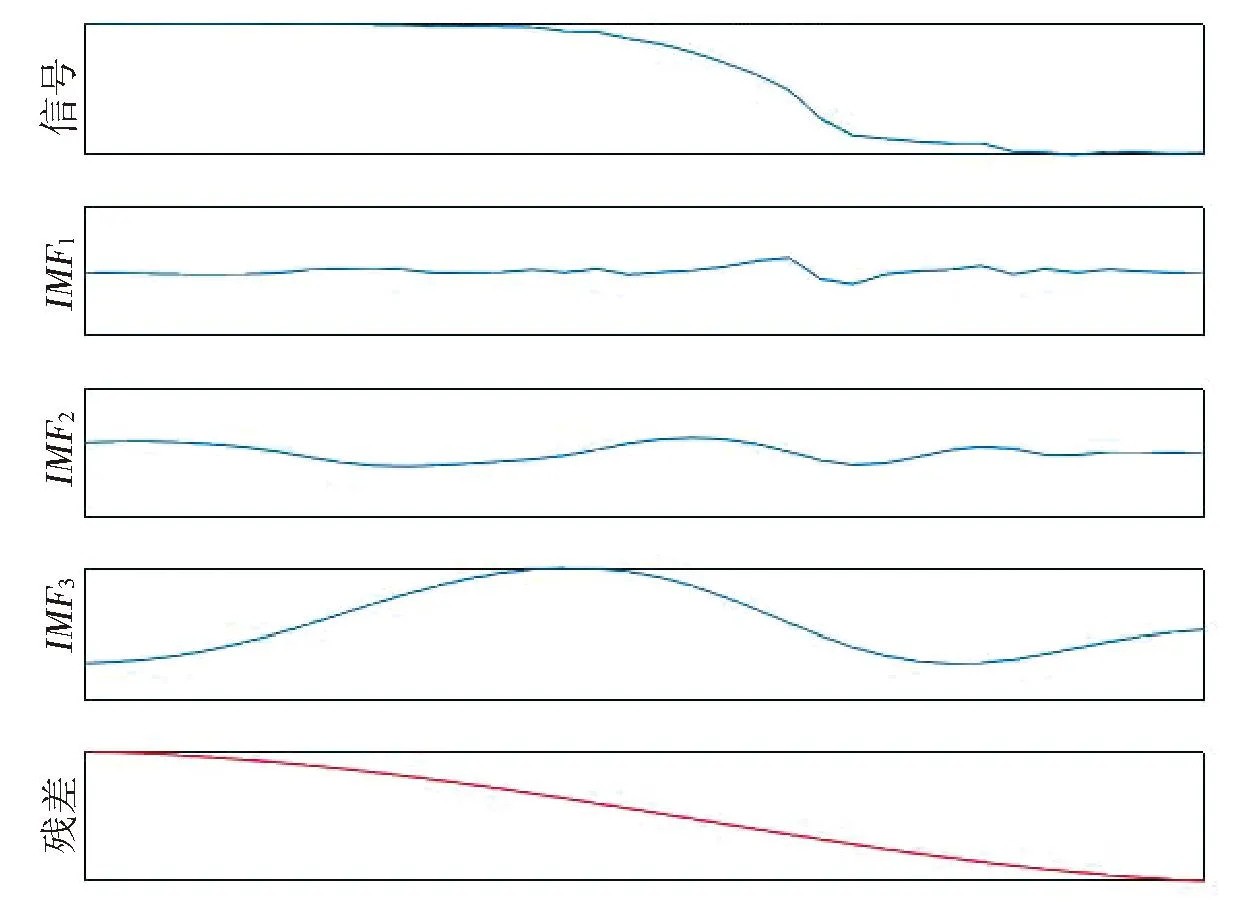
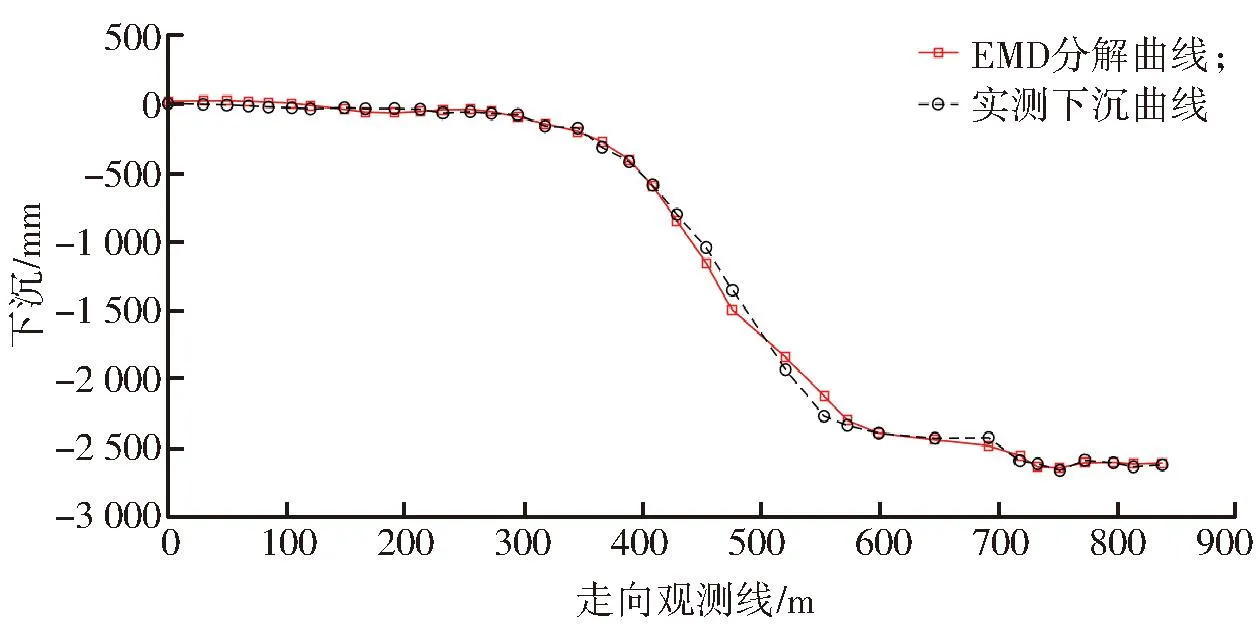
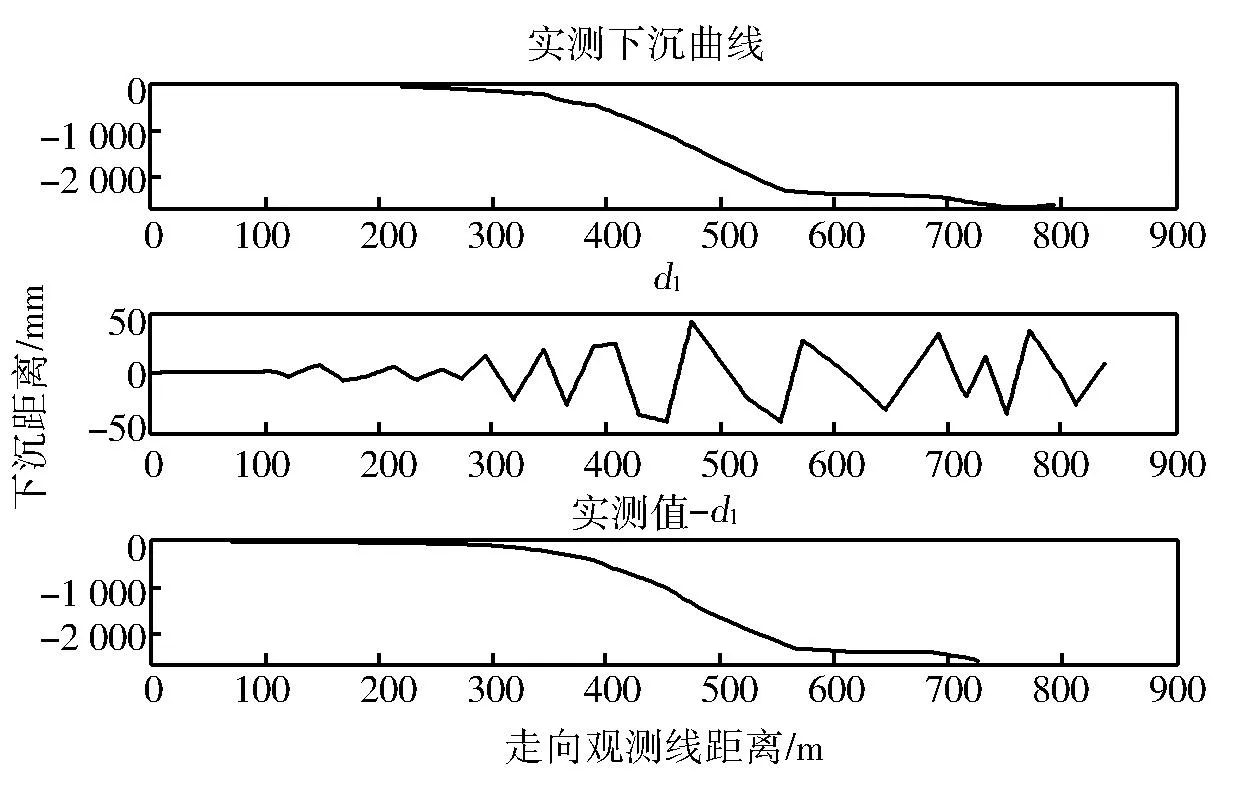
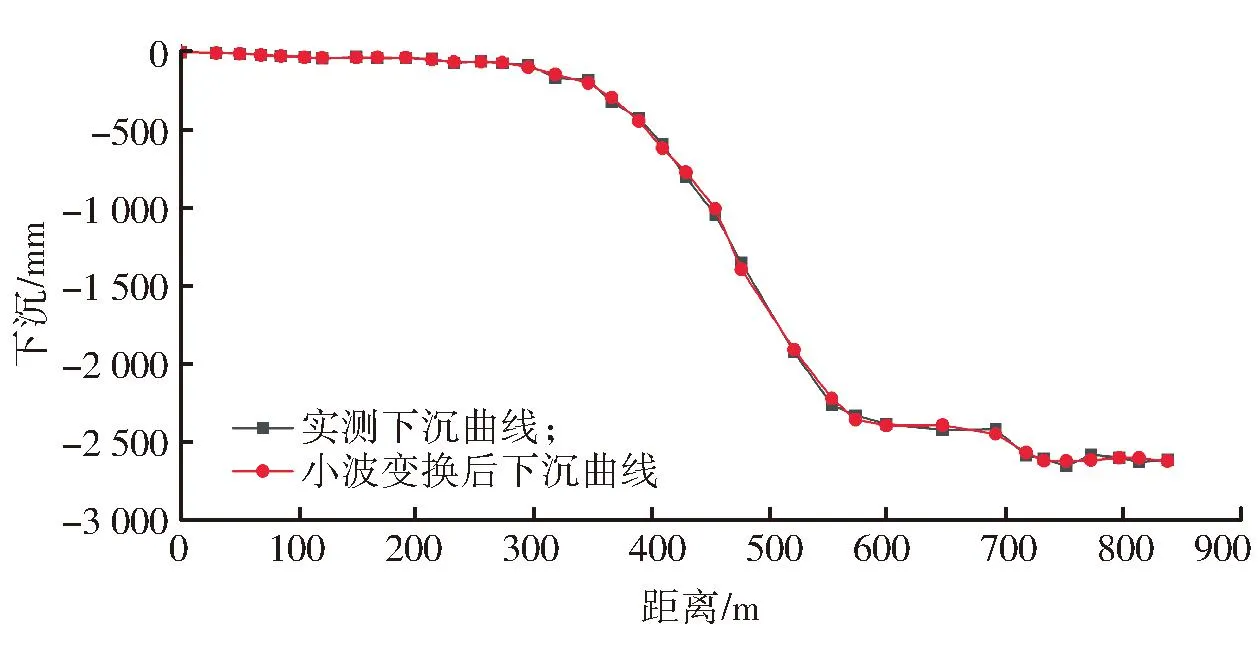
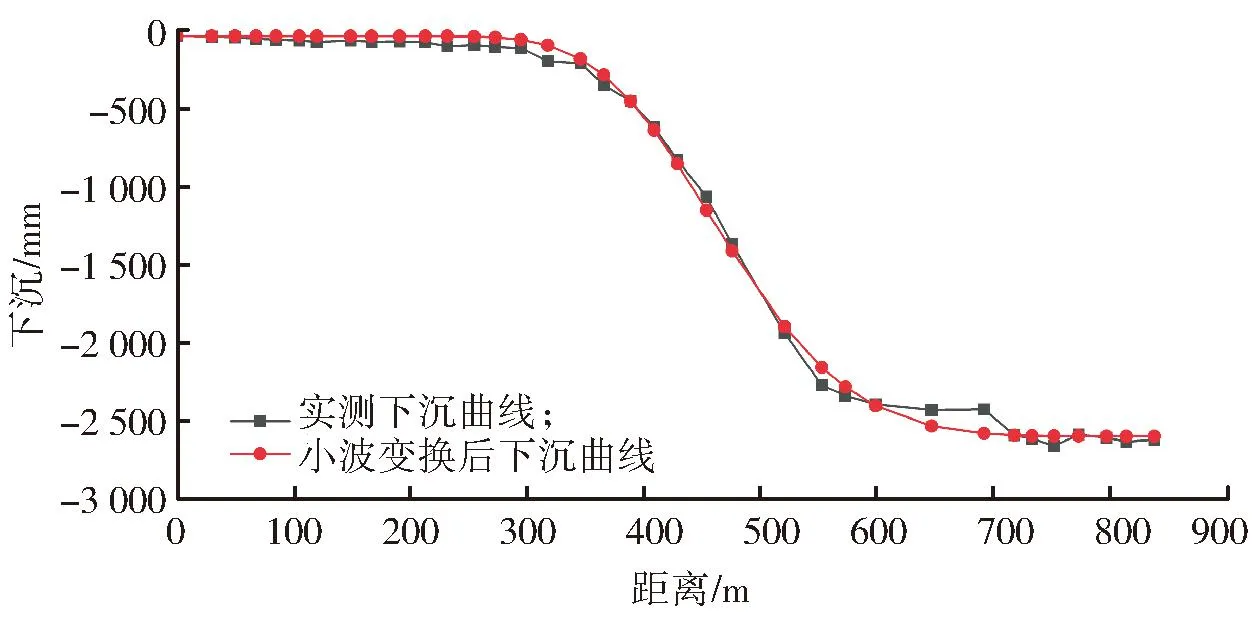
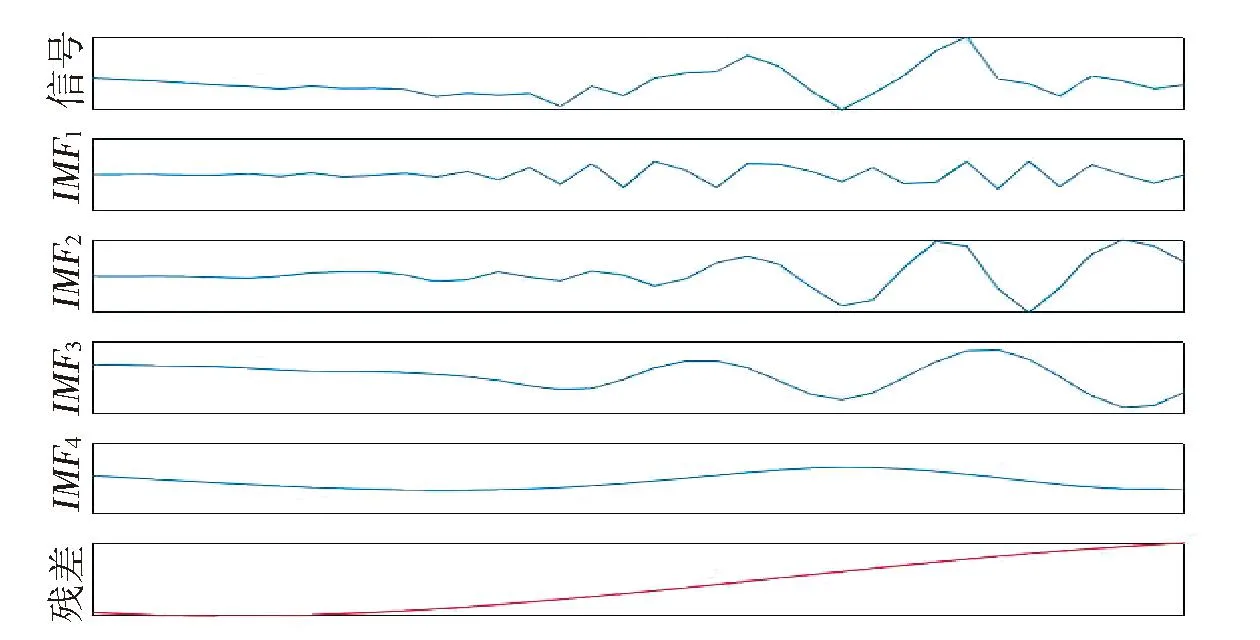
设区间[a,b]上有n个节点,a=x1 图4 三次样条高程异常曲线Fig.4 Elevation anomaly curve of cubic spline 多项式拟合是基于最小二乘原理采用n次多项式去拟合包含训练样本点在内的所有观测点[6]。本次样本点数为7个,最高可进行6次多项式拟合,为对比不同多项式阶数的拟合效果,分别进行4次、5次和6次多项式拟合,拟合结果如图5所示。 图5 多项式高程异常曲线Fig.5 Polynomial elevation anomaly curves 根据本案例中选取的7个样本点和29个检查点,分别进行上述三次样条拟合和4次、5次、6次多项式拟合,根据拟合结果得出拟合精度如表1所示。 从表1中可知:①拟合精度最高为5次多项式拟合和三次样条拟合,4次和6次多项式拟合精度最差,说明多项式阶次越高并不代表着拟合效果越好;②在实际观测中,若仅观测地形拐点,无法确定多项式阶次取何值时的拟合效果最好,因此采用三次样条拟合比采用多项式拟合更合理;③在实际观测时仅需采用三角高程或水准观测地形拐点处的高程,极大地提高了观测效率。 表1 拟合精度统计表Table 1 Fitting accuracy 针对开采沉陷中用GPS 代替四等水准测量时所存在的两个问题,在上一节研究中指出,可在仅采用三角高程或水准观测地形拐点处的高程的情况下,采用三次样条拟合法获取全观测线的高程异常值,但仍需解决GPS自身观测精度低于四等水准的问题。 针对这一问题,本文以地表稳定后走向下沉曲线上36个观测点的作为研究对象,分别采用常规的EMD、小波分析以及改进的下沉剖面函数3种方法对其GPS监测成果进行处理分析,并根据三角高程的观测数据对比分析不同方法的处理效果。 经验模式分解(empirical mode decomposition,EMD)方法是美国学者HUANG提出的自适应信号分析方法[7]。EMD方法认为,任何复杂非平稳信号都是由简单的非正弦函数分量信号组成的,一维信号x(t)可分解为多本征函数imf和分解余量r,如公式(1)所示。 将GPS观测的下沉值看作是由开采引起的下沉信号和GPS观测的误差信号构成的序列,图6给出了下沉值分解的本征函数曲线,由于GPS观测的下沉曲线主要受采动影响,故将本征函数imfi作为GPS观测误差予以剔除,其余项为采动引起。 (1) 图6 EMD分解图Fig.6 Decomposition diagram of EMD 图7显示了EMD拟合得到的下沉曲线。从图中可看出:斜率变化小的下沉曲线前半段和后半段拟合效果较好,中间段(400~600 m)偏离观测值较远。 图7 EMD拟合下沉曲线Fig.7 Fitted subsidence curvesof EMD 小波变换的过程为:首先将原始信号进行多尺度划分为高频和低频小波系数,并逐层分解低频小波系数,然后对每层的高频小波系数进行阈值处理,最后将小波系数进行重构,即滤除噪声的信号[8]。 将GPS观测的下沉值看作是由开采引起的下沉信号和GPS观测的误差信号构成的序列,GPS误差可看成是高频项,此处仅进行一层的小波分解。 1)将GPS实测下沉值通过小波变换分解为a1和b1,如图8所示。 2)设定阈值,根据误差传播定律,h=h末-h首,计算出下沉值的限差56 mm,将其作为阈值。 3)对分解项进行重构,得到下沉曲线的估计值,如图9所示。 从图中可看出:经小波变换处理后下沉曲线整体拟合较好,但在下沉曲线以300 m为界的前段和后段,d1项(即误差项)的大小明显不同,这与测量误差的随机分布不符。 图8 小波分解图Fig.8 Wavelet decomposition diagram 图9 小波变换后下沉曲线Fig.9 Subsidence curves after wavelet transform GPS实测下沉曲线可看成是由规律性下沉曲线、非规律性下沉曲线和观测误差曲线组成,规律性下沉曲线是满足下沉剖面函数的曲线,占主要成分;非规律性下沉曲线主要由地形变化、特殊地质构造、煤层倾角变化等因素引起。与非规律性下沉曲线相比,GPS观测误差存在于每个观测点且符号具有随机性,即具有高频特征,观测误差的绝对值是有限的,经误差传播定律推导,本案例中GPS实测中误差为28 mm。 由于前面EMD和小波变换2种方法是直接对实测下沉曲线进行处理,导致分解的高频曲线(即误差曲线)中含有部分非规律性下沉曲线,使得误差滤除不理想。针对这一问题,本文提出了一种下沉剖面函数-EMD的误差滤除方法。首先依据剖面函数法和山区下沉盆地主断面地表下沉预计公式迭代计算出规律性下沉曲线,将残余曲线(由非规律性下沉曲线和误差曲线组成)应用EMD方法进行分解,根据2种曲线的特点,分离出误差曲线。 剖面函数法是以某些函数来表示各种开采条件下主断面移动变形分布情况,与概率积分法相比,剖面函数法更适用于表示主断面移动变形情况。目前我国使用最多的剖面函数为负指数函数法,是由煤炭科学研究总院唐山分院根据我国大量实测资料建立的,其下沉表达式如下[9]。 (2) 式中Wm为最大下沉值,m;a为陡度参数;b为形状参数;c为位置参数;h为平均采深,m。 由于山区地表变形与平原有较大的差异性,根据相关文献,山区下沉盆地主断面地表下沉预计公式如下[10]。 W=W1+b2W1tg2α. (3) 其中,坡度影响系数函数 b2(x)=1/[a(x/r)+t]. (4) 式中,W1为类似地质采矿条件下平地下沉值;α为地面倾角;a、t为待定系数;r为主要影响半径,m。 公式(2)中W(x)是不受地形影响的下沉值,即公式(3)的W1,将公式(2)带入公式(3),并将式(3)中的a、t分别替换为d、f,即可得到改进的下沉剖面函数,如公式(5)所示。 (5) 将所有的GPS实测数据应用概率积分法及最小二乘法计算出Wm和r,并作为初始值带入公式(5),根据收集的工作面资料确定平均采深h和每个观测点的地面倾角α,带入公式(5),应用最小二乘法求解待定系数a、b、c、d、f。将拟合结果作为观测值再次求解Wm和r,直至待定系数没有明显变化为止。下沉剖面函数法拟合出的规律性下沉曲线如图10所示。 图10 剖面函数法拟合的规律性下沉曲线Fig.10 Regular subsidence curves fitted by section function method 将GPS实测下沉曲线减去规律性下沉曲线,即为残余曲线(由非规律性下沉曲线和误差曲线组成),应用EMD方法进行分解,图11给出了EMD分解的本征函数曲线,由于误差曲线具有高频特征,且各观测点中误差为28 mm,故将IMF1作为GPS观测误差予以剔除,其余项为非规律性下沉曲线。图12给出了下沉剖面函数-EMD方法的拟合效果,从图中可看出:经下沉剖面函数-EMD方法处理后下沉曲线与三角高程观测的下沉曲线拟合较好。 图11 EMD分解图Fig.11 Decomposition diagram of EMD 图12 下沉剖面函数-EMD方法拟合下沉曲线Fig.12 Subsidence curves fitted by subsidence profile function-EMD method 将36个观测点的三角高程观测数据作为真值,分别对比GPS观测数据、三种方法的拟合数据,统计结果如表2所示。 从表2中可看出: 1)GPS直接观测数据中误差为21 mm,不能满足四等水准的精度要求。 2)EMD和小波分析方法能提高GPS观测数据的精度,但由于规律性下沉占主要成分,分解出的误差项含有部分非规律性下沉,导致精度提高有限。 3)下沉剖面函数-EMD方法的精度要好于小波变换和EMD方法,根据《工程测量》中山区水准线路闭合差的规定,按3测站观测一个测点,可推算出测点中误差最大为10.4 mm,满足四等水准的要求。 表2 拟合精度统计表Table 2 Fitting accuracy 1)通过分析山区高程异常分布规律,提出了基于观测线地形拐点的高程异常拟合方法,对比发现,三次样条方法适用性更强,中误差可将至3 mm,在保证精度的同时减小了三角高程的工作量; 2)根据实际观测情况,文中提出了基于下沉曲线的下沉剖面函数-EMD的GPS数据处理方法,通过对比EMD、小波变换和下沉剖面函数-EMD3种方法的最终拟合精度可知,下沉剖面函数-EMD方法精度最高,中误差为8 mm。 3)通过文中提出的方法进行GPS数据处理,研究案例中按每3测站观测一个测点可推算出测点中误差最大为10.4 mm,可达到四等水准的精度要求,可为类似山区开采沉陷的工程应用中提供借鉴。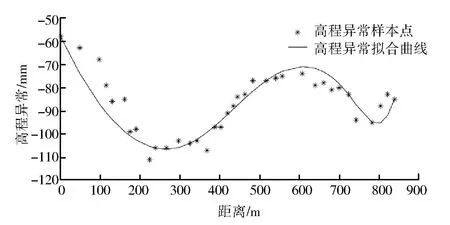
2.3 多项式拟合
2.4 拟合精度分析
3 基于下沉剖面函数-EMD的GPS数据处理方法
3.1 EMD方法
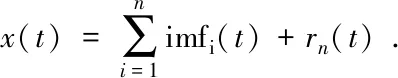
3.2 小波变换方法
3.3 下沉剖面函数-EMD方法
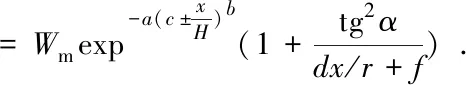

3.4 拟合精度分析

4 结论
——工程地质勘察中,一种做交叉剖面的新方法

