注重课堂动态生成,点燃学生思维活力
张海涛


课堂动态生成是在教学过程中生成的预设以外的教学活动的概括,体现了课堂教学的生动性和可变性,动态生成是对课前预设的补充和完善.在课堂教学中教师根据学生的认知规律和特点,组织学生参与探究活动,激发学生的思维活力,使课堂教学更加精彩纷呈,让课堂教学结构更加符合新课程的理念,促进学生的全面健康发展.
1 精心预设,提供精彩生成前提
课前预设与课堂生成共同构成了教学的统一体,二者相辅相成,缺一不可.课前精心预设是对教学目标、教学内容和教学活动进行的有效准备,不是对学习标准答案的预设,也不是对学生思维活动设置的条条框框.精心的课前预设能够使课堂教学更加具有灵性和魅力,促成更加有效的课堂动态生成.
案例1 以一道问题的教学为例
问题 求出图1中空白部分的面积.
课前预设:(1)如图2,运用几何方法,将图形直接平移进行求解.
(2)根据学生的习惯运用代数思想进行求解,空白部分的面积等于3×4-1×3-1×4+1×1=6.
(3)结合图3进行变式练习,在求解常规图形面积的基础上进一步求解特殊图形的面积,拓展学生的视野,发展学生的思维.
教学解析:课前的精心预设并不是设计教学过程中的每一句话或者仅仅是对各教学环节的时间分配进行静态估算,而是保持开放的心态,对多种教学活动进行充分预设.尤其是要立足学情,尊重学生的差异,着眼不同层次的学生在课堂活动中可能出现的问题以及相对应的教学策略和教学方法.如,在本课教学中笔者以为学生已经掌握了利用几何图形的平移解决问题的方法,在求解图4
阴影部分的面积时,预设会采用图5的方案.但是在提问时发现,学生仍然采用了代数方法进行求解,并且思路清晰.而笔者在课前预设时没有想到这种方法,于是,即兴在黑板上画出了图6,通过图形演示,帮助学生完成了解题过程.
2 和谐课堂,打造精彩生成氛围
当前课堂教学越来越关注学习过程的体验,在体验知识的形成和发展过程中呈现课堂动态生成,涌现出新的思想和新的创意.精心的预设为课堂生成提供了前提,而课堂和谐的教学艺术则决定了课堂生成是否足够精彩.活跃的课堂气氛能够激发学生的思维,调动学生的主观能动性,激发学生的表达和感受.因此,教师要积极营造良好的课堂氛围,营造平等交流的环境,使学生能够主动积极地参与课堂活动,乐于表达.
案例2 一元一次方程的应用
情境:在一次集体露营活动中,师生正在忙着分发碗筷.
生1:老师,今天我们一共多少人吃饭?
师:我们一共准备了55个碗,其中每个人一个饭碗,两个人共用一个汤碗,三个人共用一个菜碗,请你算一算一共有多少人吃饭?
追问:你们觉得用什么办法能够快速计算出吃饭人数呢?
同学们听了这个故事都积极思考,踊跃发言.
教学解析:上述案例2采用了生活中的例子进行导入,能够使学生迅速将新知的学习与现实生活结合起来,激发学生的学习兴趣.案例2中通过每个人使用不同种类的碗计算碗的总量,从而计算出吃饭的人数.在教学中运用即时的生活实例创设情境,激发学生的智慧,促进动态生成.
3 活动探究,推动认知结构动态生成
数学知识的学习不能仅仅依靠单纯的记忆和模仿,而要在活动中操作实践、体验探究和合作交流.在教学中引导学生通过体验探究的方式获取知识,让学生主动发现问题、分析问题和解决问题,落实学生的主体地位,使学生真正参与学习活动的全部过程,推动学生的认知结构在体验和感悟中实现动态生成.
案例3 剪纸活动
活动设计:如图7,按要求将一张长方形纸片进行折叠和剪裁.(学生动手操作,兴趣浓厚.)
问题设计:
问题1 经过剪裁之后,你得到了什么图形?请说一说你的理由.
问题2 你得到的正方形是最大的吗?你能想到其他剪成正方形的方法吗?请大家分组操作.
教学解析:问题1,学生只需要根据自己的操作结果进行回答,但是在说明理由部分,学生有些困难.教师可以引导学生通过实际测量的方式验证自己的判断.问题2引导学生通过分组交流的方式进行探索和思考,激发学生的学习兴趣,让学生能够发挥自己的潜能,思考更多的剪纸方法.通过活动探究的方式激发学生在体验中思考,激活了学生的思维,使学生从认知冲突中进一步完善自己的认知结构,从而在解决问题的过程中发挥创意,产生更加丰富的动态生成.
4 有效引导,激发精彩生成的呈现
弗赖登塔尔强调,最好的学习活动是在“做”中学.通过动手实践,学生能够产生直观的体验和感受,从而经历数学知识的产生与发展过程.教师要关注学生在操作实践中迸发的思维火花,积极引导学生进行深入思考,拓展教学资源,促进精彩生成的呈现.
案例4 算术平方根概念教学
师:小华的奶奶买了两块面积为1 m2的正方形布料准备做成一块桌布,小华家的桌面是面积为2 m2的正方形,现在奶奶按照图8将两个正方形进行拼接,虽然拼成的图形面积和桌面相等,但是形状却不匹配,你能帮奶奶想想办法吗?
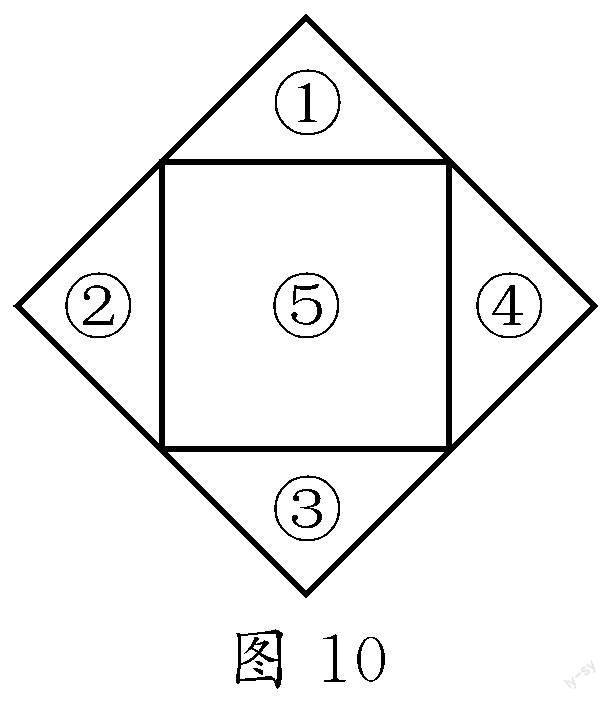
学生动手实践:用剪刀将两张边长相等的正方形纸片进行剪裁,利用已有的知识进行拼接,得到了如图9和图10两种方案.
师生互动交流,总结归纳,运用正方形的轴对称和中心对称性质,分割正方形可以解决上述问题.
师追问:现在奶奶虽然已经知道了怎么进行拼接,但是对于具体的尺寸还不太清楚,你们能帮她算一算面积为2 m2的正方形的边长是多少吗?
生1:设大正方形的边长为x,根据已知条件可得x2=2.
生2:因为12和22分别等于1和4,由此可以估算出1<x<2.
生3:因为x既不可能是整数,也不可能是分数,所以我认为不存在这样的数.
生4:现在只有解方程x2=2,才能计算出大正方形的边长,但是这种方程根据我们已有的知识还不会解,需要学习新的知识.
教学解析:本案例首先引导学生运用正方形的性质进行剪裁和拼接,将两个小正方形变成一个大正方形,进而教师进行问题引导,要求计算大正方形的边长.由于学生还没有学习算术平方根的知识,因此突破了学生已有的知识结构,引发了探究新知的好奇心.
综上所述,教学是动态的师生互动过程.由于学生的差异性,因此课堂上会出现与课前预设不同的意外生成,教師要善于捕捉有效的资源,激发学生创新的思维火花.在教学中只要进行精心的课前预设,运用动态生成的观点及时调整教学策略,激发学生的创造意识,就能成就愈加精彩的课堂.

