基于双注意力机制的成绩预测
张文娟,张 彬,杨皓哲
(同济大学机械与能源工程学院,上海 201800)
随着教育信息化的发展,教育数据挖掘逐渐成为了教育行业关心的重要课题[1]. 教育数据挖掘旨在通过对海量的教育数据的分析,发现隐藏其中的规律和联系,从而帮助教育者更好提高教育质量和教学水平. 合理的学生成绩预测被认为能够有效帮助学生提高学习成绩.
为了实现该目标,Okubo等[2]提出成绩预测分析系统应包含以下三个功能:学习成绩预测、确定成绩重要影响因素、确定反馈时间. 准确的成绩预测可以提前预见学生的最终成绩从而帮助学生避免最坏结果;重要影响因素的确定可以帮助学生有的放矢的改进学习方法,提高学习成绩;合理的反馈时间点既可以较准确的预测学生成绩,又可以给学生留下足够的反应时间. 目前国内外大多数研究也都是围绕这三个方面展开. 例如,Pandey等[3]构建了决策树模型对学生学习成绩进行预测,但仅使用信息增益率筛选了相对重要的影响因素进行预测,没有考虑所有因素;Okubo等[4]对比了循环神经网络(RNN)与传统回归分析对学生成绩的预测效果,得出了RNN网络早期预测效果更优的结论;Lu等[5]利用主成分回归法来实现学生成绩的预测,并且通过设置多时间段对比实验实现了反馈时间的确定;Aydodu等[6]在对前人研究方法进行整理对比的基础上得出利用人工神经网络进行学习成绩预测的方法具有更高精度的结论;李梦莹等[7]利用注意力机制的神经网络解决了成绩重要影响因素的确定问题,但没有考虑对学习者的及时反馈;Hassan等[8]的研究中以五周为间隔设置等距实验点,通过对比实验找到了合适的预测与反馈时间点;杜欣远[9]在研究中按照数据集的时间跨度进行平均分割来确定预测点,并对比预测效果来选择预测与反馈时间点;Waheed等[10]利用神经网络算法,通过多时间段对比实验找到了满意的反馈时间点,既达到了较高的预测准确率,又留给学生足够的反应时间.
分析以上文献,可以看出在成绩预测问题上神经网络算法比传统算法更具优势,同时大多数研究都是基于不同学习行为等因素对学习者影响程度一致的假设展开,并且对时间因素、反馈时间确定等方面研究较少且存在程序繁琐、结果普遍性差等问题,缺乏快速有效寻找合理预测与反馈时间点的方法. 同时,Baker[11]在研究中指出,学习者使用学习软件时的点击率、回复水平以及时间、顺序等多个因素均在教育数据的研究中起着重要作用. 因此,如何更全面准确地利用学习行为和时间序列等数据来对学生成绩进行预测,如何能够在较高预测准确度下快速找到较早的预测时间点,并将较为重要的学习行为反馈给学习者,已经成为亟需解决的一些问题. 对此,本文提出了一种集成了属性特征注意力机制、时间步注意力机制、GRU和一维CNN的基于双注意力机制的GRU-CNN神经网络模型(dual-attention-GRU-CNN,DA-GRU-CNN),在实现较高准确度的学生成绩预测、确定成绩重要影响因素的同时,快捷地确定反馈时间点.
1 问题描述与假设
虚拟学习环境(virtual learning environments,VLE)为学习者提供了一个资源丰富的网络学习平台,同时也记录了学习者的学习行为数据. 本文利用VLE中保存的学习行为数据,对学习者的期末成绩进行预测,同时将不同的学习行为和学习周期内各时间段对学习者期末成绩的影响程度进行可视化分析,从而找到重要的学习行为和可以及时对学习者进行反馈的时间点.
为有效描述基于VLE的大数据预测,做出以下假设:
(1)VLE准确记录了学习者在学习过程中的点击流轨迹,不存在记录错误、遗漏的情况.
(2)每个学习者都具有独一无二的学号,记为学习者i,设n为学习者的个数,V为在线学习者的集合,有|V|=n.
(3)课程期末进行考试,最终成绩y分为Distinction(优秀)、Pass(及格)、Fail(不及格)、Withdrawn(弃考)四个等级,记为Y=(y1,y2,y3,y4)T,其中y1,y2,y3,y4取值为0或1,且y1+y2+y3+y4=1.
(4)不同学期开设的同一门课程内容完全一致,C为课程集合,m为课程数量,g表示第g门课程,则C={cg|g=1…m},P为学期集合,q为学期数,h表示第h学期,则P={ph|h=1…q};同一学习者能且只能在不同学期选修同一门课程,同一学习者选修的不同课程或不同学期的同一课程视为不同记录,记为Ci,g,h,表示学生i在第h学期选修课程g的记录.
(5)设一门课程包括k个学习周,T为学习周的集合,|T|=k,t表示第t周.
(6)学习者学习特征信息:设X∈Rn*k*d表示学习者的学习行为特征,n为学习者数量,k为学习者学习行为特征的时间步长度,d为学习者学习行为特征向量的维度,l表示第l个维度.
(7)学习行为特征:设Ai∈Rk*d表示学生i的学习行为特征,即有X=[A1,A2,…An],该数据通过虚拟学习系统的日志文件获取.
(8)对学习者的反馈是静态的,即对学生仅进行一次反馈,不考虑学生因获得反馈调整学习活动后继续进行反馈的情况.
2 模型算法描述
本文旨在对VLE系统中存储的教育数据进行挖掘与分析,实现对成绩的准确预测,并分析出影响不同学生最终学习成绩的关键学习时段和学习行为中的重要影响因素. 根据Aydodu等[6]的结论,在学生成绩预测方面人工神经网络模型比传统预测方法具有更好的性能,因此本文以神经网络为基础来实现对学生成绩的预测. 同时,考虑到不同学习行为和不同时间阶段对最终学习成绩的影响程度是不同的,本文分别针对学习者的学习行为属性特征和学习的时间步特征加入注意力机制,来赋予各学习行为特征和时间步特征对结果影响的合适权重,从而解决了数据的不同属性特征和时间步对最终结果重要性不同的问题,实现了对信息更为充分的利用. 另外,本文集成了GRU模型和一维CNN模型对时间序列数据处理的优势,将其联合起来引入到VLE大数据分析中,取得了较好的预测精度.
本文所提出的集成了CNN与双注意力机制GRU的模型(DA-CNN-GRU)结构框架如图1所示,模型主要包含6层:输入编码层(input embedding layer)、属性特征注意力层(attribute attention layer)、GRU层(GRU layer)、时间步注意力层(timestep attention layer)、卷积层(CNN layer)、标签预测层(label prediction layer),图中Acquiring data表示原始数据集,Dimension Attention 表示属性维度注意力模块,Timestep Attention表示时间步注意力模块,Global AvgPool表示全局平均池化模块,Concatenation表示特征融合模块,MLP表示多层感知机模块.
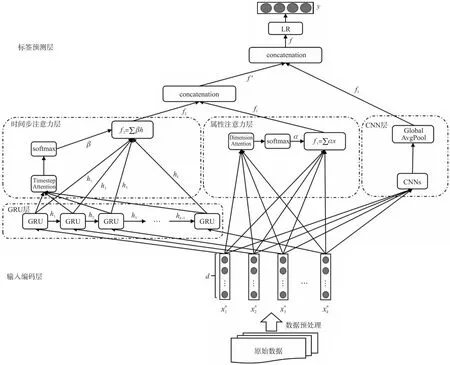
图1 DA-CNN-GRU 模型结构图
2.1 输入编码层
输入编码层主要是对输入数据中的各属性值以及监督学习情况下的标签进行编码预处理. 本文采用因子分解(factorize)方式对学生行为属性进行编码. 预测标签分为四类(优秀、及格、不及格、弃考),对此采用one-hot编码. 从而生成学生i的特征矩阵Ai∈Rk*d和成绩向量yi.
(1)
Y=(y1,y2,y3,y4)T,
(2)
式中,d为学生学习行为的属性特征向量,在本文中固定为20;k为学生学习行为的时间步向量,在本文中固定为38;y1,y2,y3,y4取值为0或1,其中有且只有一项为1.
2.2 属性特征注意力层
通过对各属性特征进行编码后,可以得到特征矩阵A和标签Y.考虑到学习行为的不同属性特征对最终成绩的影响程度不同,本文设计了属性特征注意力机制来解决该问题.属性注意力机制是根据各学习行为属性与最终成绩之间的关系,为各属性特征分配合适的注意力权重,从而解决不同属性因素对学生最终成绩的影响程度不同的问题.本文采用多层感知机(multi-layer perceptron,MLP)来进行注意力权重的分配,将学生特征矩阵A中的每一列向量Al视为对应属性特征向量,即Al=(a1,l,a2,l,…,ak,l)T,代表了第l种学习行为的特征向量,at,l代表行为l的第t维.由于每个学生都记录有共k周的行为数据,因此每一个行为都具有k个维度,从而利用MLP可以得到任意学习行为特征向量Al的注意力权重αl,具体计算过程为:
ul=MLP(Al),l=1,2,…,d.
(3)
用归一化指数函数(softmax)对所得权重进行归一化处理,得到各学习行为特征的注意力得分αl=(α1,α2,…,αd),该过程可以形式化表示为:
(4)
式中,αl指第l个学习行为特征的注意力得分,该得分越高则代表该学习行为对学生最终成绩的影响程度越大,因此向量α可以反映在学习过程中不同学习行为的重要程度.将各学习行为注意力得分向量α与学习行为特征矩阵A中对应位置的学习行为特征值进行加权求和,得到学生属性特征f1,具体计算过程为:
(5)
2.3 GRU层
GRU网络是RNN的一种特殊形式,本文用其来处理学生行为的时间步信息,GRU可用式(6)~(9)描述:
zt=σ(Wz·[ht-1,xt]),
(6)
rt=σ(Wr·[ht-1,xt]),
(7)
(8)
(9)
式中,xt、ht分别代表每个GRU的输入和输出,在本文中即代表学生i第t周的学习行为向量和经过GRU处理的第t周隐藏状态;W*代表对应的权重系数矩阵;zt、rt分别表示GRU中t时刻更新门和重置门的函数表达式;σ表示sigmoid激活函数,其输出值的取值范围为[0,1];tanh表示双曲线正切激活函数.将经过输入编码层处理的学生特征矩阵A中的每一行向量Aj*视为对应的时间步向量,即Aj*=(aj,1,aj,2,…,aj,d),代表了第j个时间步即第j周,aj,l表示第j个时间步的第l个学习行为.由于VLE系统中共记录了d种学习行为,因此每一个时间步都包含d维.把每一个学生的Aj*输入GRU层,通过输出每个GRU在t时刻的状态ht来实现对时间序列数据的编码ht=(ht,1,ht,2,…,ht,d)T,t=1,2,…,k.
2.4 时间步注意力层
为了解决不同时间段的学习数据对最终成绩影响不同的问题,本文对GRU层传递的编码数据h进行时间步赋权,并且可以找出对学生最终成绩影响较重时间段,实现及时反馈.学生第t周行为特征向量xt经过GRU层的处理得到隐藏状态ht,其可以视为利用GRU完成的一种编码. 该层采用MLP实现对编码ht进行注意力权重的分配,从而计算出各时间步的注意力权重βt.具体计算步骤为:
vt=MLP(ht),t=1,2,…,k.
(10)
用归一化指数函数(softmax)对所得权重进行归一化处理,分别得到各时间步的注意力得分β=(β1,β2,…,βk),该过程可以形式化表示为:
(11)
式中,βt指第t个时间步的注意力得分,该注意力得分越高则表明对应时间步的行为对学生最终成绩影响越大,因此可以根据注意力得分向量β来确定反馈时间.将注意力得分向量β与对应的GRU编码后的时间状态h进行加权求和,得到学习行为时间步特征,具体计算过程为:
(12)
2.5 卷积层
卷积神经网络可以对原始数据进行更高层次的表达,从而达到特征提取的目的.本文采用的一维CNN结构常用于处理文本与时间序列数据[12],由数据先验可知有些时序数据之间存在一些较强的相关性,所以能够运用CNN来处理其局部特征.本文将学生特征矩阵Ai输入CNN层,利用一维CNN结构来提取学生行为的时间步数据,卷积层处理得到的学生时间步特征图Ci可表示为:
Ci=f(Ai⊗Wi+bi),
(13)
式中,Ai为学生特征矩阵.对一维CNN而言,学生行为属性维度均默认为d不进行处理,因此仅对时间步维度进行卷积操作.⊗为卷积操作,Wi为卷积核的权重向量,bi表示偏移量,f(·)为激活函数,本文设置为线性整流函数(rectified linear unit,Relu). 本文利用CNN抽取原始数据特征,挖掘多维数据之间的关系,并将处理后得到的特征图Ci输入全局平均池化层(GlobalAvgPool),按列进行平均池化操作,从而得到降维后的平均特征f3.
2.6 标签预测层
由学习行为属性注意力层计算得到的基于学习行为属性的学生特征f1,和由时间步注意力层计算得到的基于学习行为时间步的学生特征f2,是分别从两个维度进行的学生成绩预测,因此所含信息具有互补性,有必要对两个特征进行融合,以便更全面准确地利用信息对学生成绩进行预测.本文选择以串联(concatenation)方式进行特征融合,将两个维度的学习行为特征进行拼接,得到一个完整的学生特征f′,该过程可表示为:
f′=[f1;f2],
(14)
式中,[.;.]表示特征拼接操作.
为了获得更好的预测性能,对前面得到的学生特征f′和对时间步行提取得到的平均特征f3以串联(concatenation)方式进行融合,得到更丰富信息特征f,从而提高模型预测性能,该过程表示为:
f=[f′;f3],
(15)
式中,f3为f1与f2进行特征融合后形成的最终特征.
本文采用逻辑回归的多分类模式对最终特征f进行解码,利用MLP来实现逻辑回归的多分类功能,输出层使用归一化指数函数(softmax)得到各成绩预测类别Y:
Y=MLP(f).
(16)
3 实验
3.1 数据集
本文在英国开放大学提供的基于虚拟学习环境(VLE)的学习分析数据集(open university learning analytics dataset,OULAD)的基础上展开实验[13]. OULAD中共包含22门课程的数据,每门课程开课时间为38周,VLE中共记录有5种学生基本信息和20种学习行为信息,关于数据集的描述如表1所示. 本文所有实验都按照8∶2的比例将数据集划分训练集和测试集,每次实验都用训练集训练数据,并选择最优参数,最后用测试集计算各项指标.

表1 数据集描述表
本文选取OULAD数据集中代号为“FFF”的课程的全部数据,定义为数据集“FFF class”,同时引用Hassan等[8]提供的数据集“Pass-Withdraw”,两数据集中成绩分布如表2、表3所示.

表2 “FFF class”数据集成绩统计表

表3 “Pass-Withdraw”数据集成绩分布表
3.2 实验参数设置
本文所提出的模型基于深度学习框架Keras展开实验,考虑到本文所用样本数量和维度都不是很大,所以模型初步定为单层GRU后经过试验证明增加更多GRU层一方面会大大增加模型的时间复杂度,另一方面存在过拟合倾向,因此最终定为单层GRU. 为了充分提取输入样本特征,注意力层的神经元数量设定为与传入数据的第三维度数量相同,因此针对不同样本进行实验时需要根据输入样本的情况进行调整. 为了防止过拟合的产生,在注意力融合层后加入Dropout层,参数设置为0.3,该函数会随机地使一部分神经元无效,从而在一定程度上防止过拟合. 卷积层数量初步定为3,后根据张永峰等[12]提供的方法进行实验. 考虑卷积层权重分布情况和训练过程中误差变化情况,发现卷积层自第三层开始对模型训练精准度提升的贡献很小,因此最终卷积层数量确定为2层. 由于本文选取数据的时间序列最长为38,因此卷积核长度应在1到38之间选择,所以本文将第一个卷积核长度设为20,数量设为8,卷积核数量以2倍增加,所有卷积核滑动步长均设为1. 最后,采用softmax回归进行解码,由一个三层全连接网络构成,隐含层的激活函数设为“Relu”,输出层的激活函数为“softmax”. 本模型采用的优化器为Adam,网络中其余的参数均采用测试效果较好时的参数或默认参数. 网络结构的具体参数设置需根据不同的数据集的特点来进行调整.
本文采用了准确率(Accuracy)、精确率(Precision)、召回率(Recall)、F1值(F1-Measure)这四个指标进行模型性能度量. 准确率是指分类正确的样本数量占总样本数的比例;精确率表示分类正确的正例的数量占所有预测为正例样本总数的比例;召回率表示分类正确的正例的数量占所有正例样本总数的比例;F1值是精确率和召回率的调和平均值. 通常认为准确率和F1值越高,模型预测分类性能越好.
3.3 实验结果与分析
3.3.1 对比实验
将本文所提出的DA-GRU-CNN模型与支持向量机(support vector machine,SVM)、决策树(decision tree,DT)、深度长短期记忆网络(DEEP-LSTM)等三种其他学者用来解决该问题的模型[14]、[15]、[8],以及CNN、DA-GRU(双注意力GRU模型)等两个机制消融模型在“FFF class”和“Pass-Withdraw”两个数据集中进行成绩预测效果比较,以验证本文提出方法的有效性,实验结果如表4、表5所示.

表4 “FFF class”数据集实验结果对比
从表4和表5可以看出,首先,相比其他学者在该问题上使用的预测模型,本文提出的DA-GRU-CNN模型在两个数据集中均取得了较好的效果;其次,对比Hassan等[8]在该数据集上所提出的DEEP-LSTM模型,DA-GRU-CNN模型性能与其十分接近,但是模型的复杂程度远低于前者,训练时间和反应时间都大大缩短;最后,在与CNN、DA-GRU两个消融模型的比较中,本文的模型也取得了更好的效果,这说明CNN模型提取的时序特征与DA-GRU模型对时序数据编码的特征具有一定的信息互补性,因而两组特征融合后取得了更好的效果.
3.3.2 学习行为可视化分析
为了挖掘出影响学生成绩的具体因素,本文参考李梦莹等[7]的方法对学生学习行为属性特征注意力机制进行了权重可视化分析,图2为利用“FFF class”数据集进行学生成绩预测时各学习行为对最终成绩的影响程度的权重分布图. 该图横坐标代表各学习行为即属性特征编号,代表20种学习活动,纵坐标代表该行为所占权重,权重越大表示对应行为对最终成绩的影响越大,所有活动的权重之和为1. 分析图2可知,编号为1,3,9的三个学习行为对学生最终成绩影响最大,这三个行为分别为课程任务的完成次数、课程主页的浏览次数和课堂测验的完成次数. 由此可以推断出,积极完成课堂测验与课程任务,认真学习课程主页内容是提高“FFF”课程成绩的关键,在对该课程的学习者进行成绩反馈时应该重点强调这三项活动,从而达到帮助其提高最终成绩的目的.
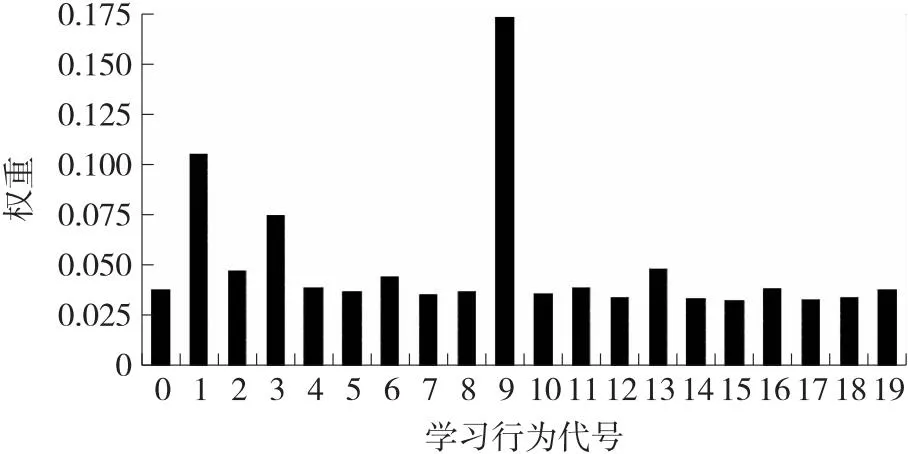
图2 “FFF class”学习行为注意力权重
3.3.3 反馈时间可视化分析
为了能够利用预测分析结果及时对学生进行反馈,从而给予学生足够的学习时间来提高学习成绩,本文在模型中设计了针对时间步的注意力机制,通过对全时间步的注意力权重可视化,来分析各时间步对学生最终成绩的影响程度,从而找到一个合适的学习周,在此周之前所有周的注意力权重之和可以达到一个较高的值,因此利用该周之前的各周数据即可以较准确的进行最终成绩预测,最终实现及时反馈.
在本文之前,不少专家学者对反馈时间的确定问题做出过研究,但大多是基于大量实验来寻找可行点,如Hassan 等[8]曾利用“Pass-Withdraw”数据集进行实验研究,寻找最佳的反馈时间段,从而达到反馈的及时性与准确性的平衡,其实验结果如图3所示. Hassan 等[8]利用其所提出的多层LSTM模型,以5周为间隔在“Pass-Withdraw”数据集上设置对比实验,图3的横坐标为模型训练次数,纵坐标表示预测学生成绩的准确率,5条线分别代表利用前5周、前10周、前15周、前20周、前25周的学生学习行为数据进行实验的结果. 实验结果显示当反馈时间选为25周时,预测学生成绩时可以取得超过95%的准确率,同时也给学生留下了13周的反应时间来提高其学习成绩,因此在第25周时对预测成绩等级处于“Withdraw”的学生进行反馈,督促其学习具有比较好的效果.
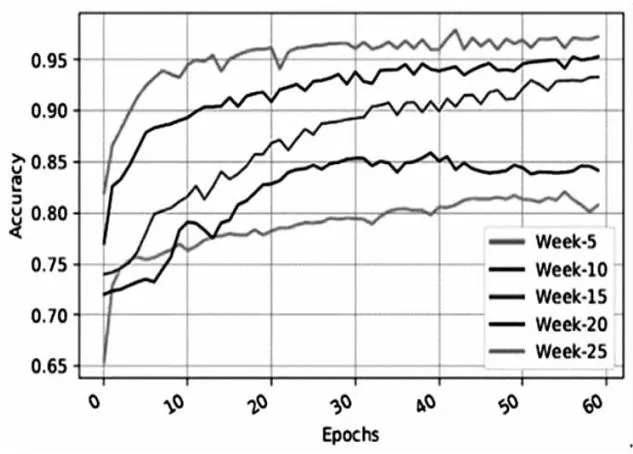
图3 Hassan团队实验结果
为了便于比较,本文也利用“DA-GRU-CNN”模型在“Pass-Withdraw”数据集上进行实验,对38周学习行为进行时间步注意力权重可视化分析,权重分布图如图4所示. 其中横坐标代表各周的标号,从0到37代表38个学习周,每一周的学习活动都会对最终成绩产生一定的影响;纵坐标代表注意力权重的大小,38周活动的权重之和为1,某一周的注意力权重越大,说明该周对学生最终成绩影响程度越大. 从图中可以看出在“Pass-Withdraw”数据集中,影响最终成绩的时间段主要集中在学期的前半部分,第26周以前各周对最终成绩的影响权重总和已经超过90%,这也解释了Hassan等的实验可以在第25周左右取得较好预测效果的原因.
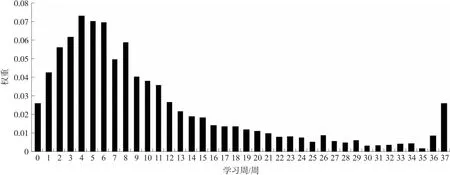
图4 “Pass-Withdraw”时间步注意力权重分布图
虽然Hanssan等的实验结果可以在“Pass-Withdraw”数据集上取得较好的结果,但是其通过定性实验分析来寻找到的结果的反馈及时性与精度的平衡点必然是十分依赖其目标数据集的,适应性较差,一旦更换数据集,就要重新进行实验来寻找平衡点. 因此,为了提升反馈的准确性,实现个性化反馈,本文利用“FFF课程”数据集继续实验,将分类实验进一步细化为二分类实验,即将“FFF课程”数据集按照学生最终成绩划分为“FFF Pass-Fail”、“FFF Distinction-Pass”和“FFF Pass-Withdraw”三组切片,从而可以对不同情况的学习者进行反馈,实现个性化学习. 本文以“FFF Pass-Fail”这个切片为例,继续展开研究,其中仅包含FFF课程中所有成绩为“Pass”和“Fail”的学习者行为数据.
首先在Hanssan等提出的第25周这一时间点展开实验,由于表4和表5已经对多种算法的情况进行了对比分析,所以此处不再赘述其他算法的性能,仅用Hanssan等使用的DEEP-LSTM模型和本文提出的DA-GRU-CNN模型进行对比,对比结果如表6所示. 结果显示,两种模型在第25周这个节点均未取得比较好的预测效果,因此可以看出对于FFF课程的“Pass-Fail”类别的学生成绩进行预测时,第25周并非反馈及时性与准确性的平衡点. 同时,在这种情况下,本文所提出的DA-GRU-CNN模型预测准确率比LSTM模型提高了接近十个百分点,再结合表4、表5的信息可以得出“DA-GRU-CNN”模型对残缺信息的利用水平要高于LSTM模型的结论. 在此基础上,继续利用“DA-GRU-CNN模型”对38周学习时长进行时间步权重分布可视化分析,结果如图5所示.

表6 “FFF Pass-Fail”25周实验结果
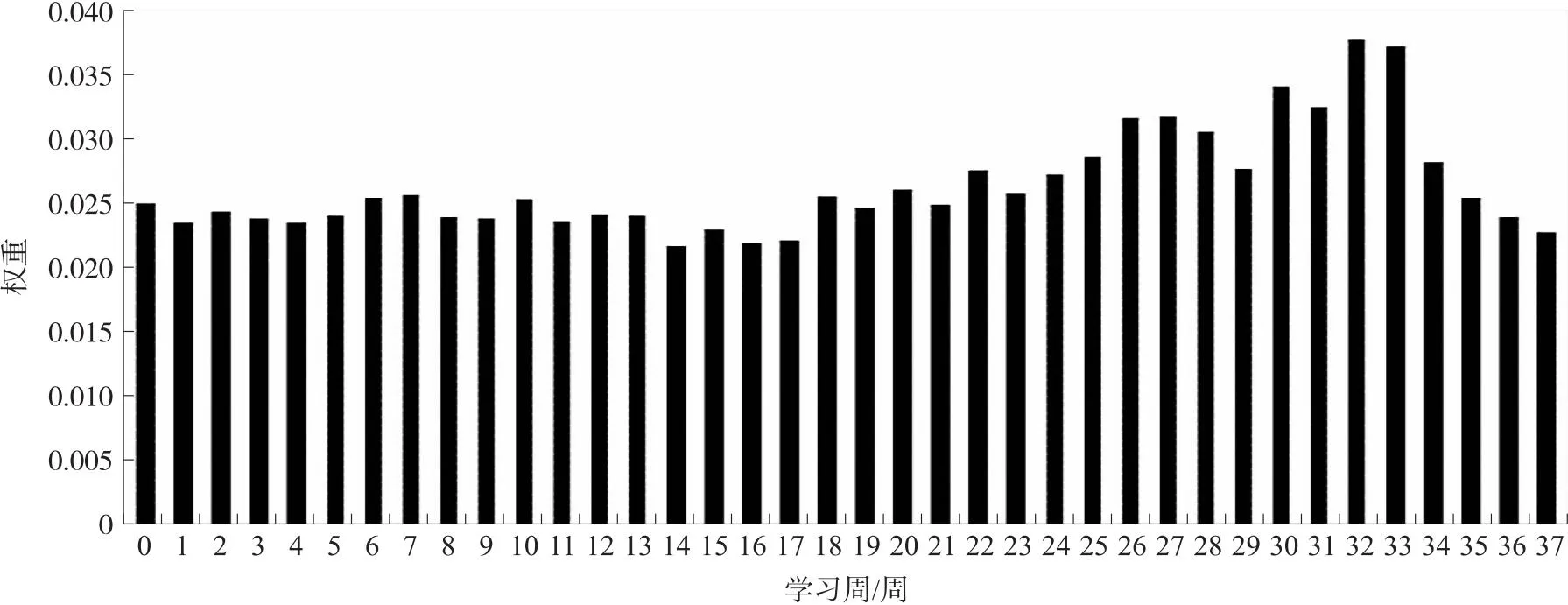
图5 “FFF Pass-Fail”时间步权重分布图
分析图5可知,当预测数据来源时间段选择为0到25周时,有大量高权重的学习周没有被包含在该时间段内,因而出现了预测准确率较低的情况. 若要取权重之和大于0.9的时间段,至少要0到33周,因此推测当反馈时间定在第33周时可以取得比较好的准确率. 为了验证推测,本文从利用0至19周的数据进行预测实验,变量梯度设置为1周,变为利用0至38周的数据进行预测,来寻找可以取得较好预测准确率水平的点,具体实验结果见图6.

图6 “FFF Pass-Fail”预测准确率变化
图6中横坐标表示周数的变化,对应周数表示利用从第0周到该周的数据进行成绩预测;纵坐标表示预测的准确率. 该图展现了DT、SVM、DEEP-LSTM和DA-GRU-CNN四个模型的预测准确率随时间增加而变化的情况. 从该图可以看出第33周以前四个模型的预测准确率随周数上升而上升幅度较大,第33周之后上升幅度较小,且第33周时预测准确率均达到较高水平,与图5所显示的权重分配比例具有较高的一致性,从而可以判定反馈时间定为第33周时可以取得预测准确率与反馈及时性的平衡.
根据以上实验可以看出,本文提出的“DA-GRU-CNN”模型在反馈时间的确定上具有更高的准确性与更好的适应性,不仅使得寻找反馈时间平衡点的过程更为简单,而且能够更好的适应不同的数据集,大大减少了寻找反馈时间平衡点的工作量.
3.4 模型适用性范围分析
在预测学习分析(predictive learning analytics,PLA)中,教育数据往往会来自不同的教育场景,如大学教育、中小学教育、MOOC平台教育等,而算法模型对不同场景的数据处理能力是不同的. Hlosta等[16]在研究中指出,预测学习分析中解决方案的结果高度取决于可供分析的数据,而这些数据取决于其来源教育机构的类型. 然而,这些方法的思路常是相通的,不同的是这些场景下的特征需要根据实际情况进行重新选择,并且大致将当前的教育机制划分为了中小学教育、大学教育、远程成人教育和MOOC教育等类型. 因此有必要对本文提出的模型进行适用性范围分析,从而改善模型的使用并促进进一步研究的展开.
为了对不同场景下的“DA-GRU-CNN”模型适用性进行测试,本文采用了由阿里云天池实验室提供的公开数据集“students-academic-performance-dataset”(后文称“sapd”数据集)对多种算法模型预测性能进行测试比较. 该数据集主要记录了中小学学生课堂表现,包含一学期内学生的八项学习行为,标记为学习行为0到7,分别代表了学生负责家长、课堂举手次数、学习资源查看次数、公告查看次数、参与讨论次数、家长参与学校调查情况、家长满意度、缺课次数. 预测结果如表7所示. 同时,利用本文所提出的“DA-GRU-CNN”模型对sapd数据集中的学习行为权重分布进行可视化分析,结果如图7所示.

表7 “students-academic-performance-dataset”实验结果
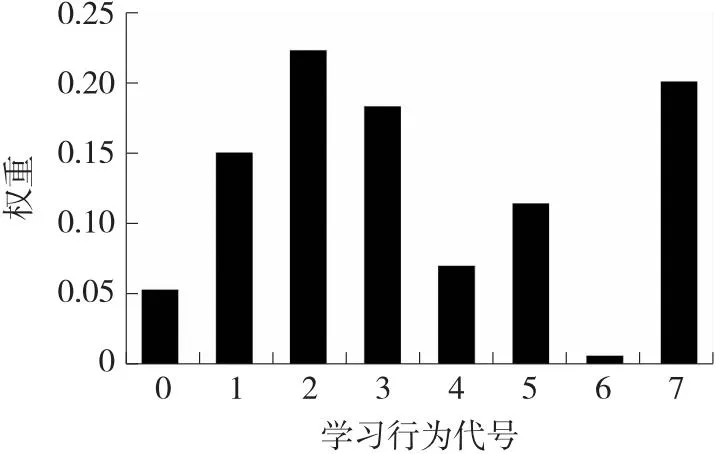
图7 “students-academic-performance-dataset”学习行为注意力权重
根据表7实验结果可知,在对该数据集的处理上,本文所提出的“DA-GRU-CNN”模型效果与其他模型相近,没有突出优势. 分析实验过程可知,由于该数据集是以学期为单位进行的总体统计,而非按照时间序列详细统计学生学习过程中的各阶段数据,因此本文所提出的模型无法完全发挥针对数据时序特征的优势. 由此可以得出结论,本文所提出的“DA-GRU-CNN”模型对数据细节要求较高,需要相关数据能够描述学习者在各阶段的学习行为特征,因此该模型需要在MOOC平台等具有强大数据搜集功能的虚拟学习环境中才可以发挥优势. 另外,从图7中可以看出,1、2、3、7这四项行为对学生成绩影响权重较大,即课堂举手次数、学习资源查看次数、公告查看次数和缺课次数这四项行为对学生成绩影响较大. 同时,对比Amrieh等[17]提出的基于信息增益的滤波器对该数据集进行特征选择的实验结果(图8),可以看出两种算法所提取的重要学习行为基本一致,由此也可以证明本文所提出算法可以较为准确的选择出对学生成绩影响较大的学习行为.

图8 Amrieh团队滤波实验结果
前文实验中采用的“FFF class”和“sapd”两类数据集分别是远程成人教育数据和中小学教育数据. 经过本文实验分析可以看出,在远程成人教育中,对成绩影响较大的学习行为主要是课程任务的完成次数、课程主页的浏览次数、课堂测验的完成次数三项活动;而在中小学教育中成绩影响较大的学习行为主要是课堂举手次数、学习资源查看次数、公告查看次数和缺课次数. 对比两者的影响行为可以发现在两种教育类型下既存在同样的重要行为又存在不同的重要行为. 首先,无论是远程成人教育中的“课程主页浏览次数”还是中小学教育中的“学习资源查看次数”都是对学生学习课程资料次数的统计. 由此可以看出,无论是远程成人教育还是中小学教育都需要重点关注学生对课程资料的学习过程. 同时,成人教育中“课程任务的完成次数”和“课堂测验的完成次数”等行为都是对学到知识的应用和练习,由此可以看出远程成人教育中对课程中学到知识的练习水平对学生成绩影响更大,而中小学教育中“课堂举手次数”“公告查看次数”和“缺课次数”等行为更多反映的是学生在受教育过程中与教育者的互动水平. 对比两者的不同可以推测由于成人和中小学生的学习意愿、精力水平等受教育对象自身特点的不同以及所学习知识的难度不同,对成绩有较大影响的学习行为也不同,因此需要针对不同受教育人群设计不同侧重的教育机制.
4 结论
本文针对虚拟学习环境(VLE)中的成绩预测与结果反馈问题进行了研究. 具体研究内容如下:(1)提出了一种基于大数据分析确定反馈时间的方法,建立了集成双注意力机制的GRU与一维CNN的神经网络模型(DA-GRU-CNN);(2)针对确定重要成绩影响因素和反馈时间的问题设计了双注意力机制GRU算法;(3)在两个公开数据集上进行了实验,结果表明本文提出的模型预测性能较好,能够有效筛选出影响学生成绩的重要学习行为,并且可以更为快捷地确定反馈时间,模型普适性更好. 后续,一方面可以对预测结果的动态反馈问题继续展开研究,从而进一步提高反馈效果,帮助学习者提升成绩;另一方面还可以针对逻辑性较强或抽象性较强的课程产生的数据分别展开研究,进一步提高模型效果.

