三角代数上Jordan同构的刻画
刘 丹,张建华,宋明亮
(1.江苏第二师范学院数学科学学院,江苏 南京 210013)(2.陕西师范大学数学与统计学院,陕西 西安 710062)
设A和B是结合代数,φ:A→B是一个线性双射.若对任意的x∈A且2x=0,有x=0,则称A是2-无挠的.如果对任意x,y∈A,有φ(x∘y)=φ(x)∘φ(y),则称φ是一个Jordan同构,其中x∘y=xy+yx为Jordan积. Jordan同构是算子代数上的一类重要的线性映射,受到了许多学者的关注. 例如:Molnar等[1]证明了三角矩阵代数Tn(F)上的Jordan同构是同构或反同构.这里F是至少包含3个元素的数域.Beidar等[2]推广了这个结论,证明了2-无挠交换环R上的上三角矩阵代数上的Jordan同构是同构或反同构. Lu[3]证明了套代数上的Jordan同构是同构或反同构. Wong[4]研究了上三角矩阵环上的Jordan同构,并给出了Jordan同构是同构或反同构的条件. 本文将通过由零积、Jordan零积或交换零积所确定的子集上线性映射的局部性质来刻画三角代数上的Jordan同构.关于线性映射的局部性质的研究主要有两个方面.一方面是逐点定义的局部映射,如局部导子和局部同构的研究[5-9].另一方面是通过线性映射在某些子集上的局部性质来研究它的整体结构性质(见文献[10-16]).
设A和B是交换环R上的含单位元的代数,M是(A,B)-忠实双边模.在通常的矩阵运算下,称
为三角代数.设U=Tri(A,M,B)是一个三角代数,1A和1B分别是A和B的单位元.记
且
Uij=eiUej(1≤i≤j≤2),
则U=U11+U12+U22且U12是(U11,U12)-忠实双边模.
1 主要定理及其证明
定理1设U=Tri(A,M,B)是三角代数,V是R上2-无挠含单位的代数.则线性双射φ:U→V是Jordan同构当且仅当φ保单位且下列条件之一成立:
(1)φ(x∘y)=φ(x)∘φ(y),其中x,y∈U满足xy=0.
(2)φ(x∘y)=φ(x)∘φ(y),其中x,y∈U满足x∘y=0.
(3)φ(x∘y)=φ(x)∘φ(y),其中x,y∈U满足xy=yx=0.
以下假设φ:U→V是一个满足定理1条件(3)的保单位线性双射.为证明定理1,我们需要以下几个引理.
引理1对任意幂等元p∈U,有φ(p)=φ(p)2.
证明对任意幂等元p∈U,由p(1-p)=(1-p)p=0得
0=φ(p)∘φ(1-p)=2(φ(p)-φ(p)2).
从而φ(p)=φ(p)2.证毕.
引理2设uij∈Uij(1≤i≤j≤2),则
(1)φ(uii)=φ(ei)φ(uii)φ(ei);
(2)φ(u12)=φ(e1)φ(u12)φ(e2)+φ(e2)φ(u12)φ(e1).
证明(1)由于u11e2=e2u11=0,则
φ(u11)φ(e2)+φ(e2)φ(u11)=φ(u11)∘φ(e2)=0.
(1)
从而由引理1和式(1)可得:
φ(e2)φ(u11)φ(e2)=φ(e1)φ(u11)φ(e2)=φ(e2)φ(u11)φ(e1)=0.
因此,
φ(u11)=φ(e1)φ(u11)φ(e1)+φ(e1)φ(u11)φ(e2)+φ(e2)φ(u11)φ(e1)+φ(e2)φ(u11)φ(e2)=
φ(e1)φ(u11)φ(e1).
类似地,我们有φ(u22)=φ(e2)φ(u22)φ(e2).
(2)显然,对任意v12∈U12,有
φ(u12)∘φ(u12)=0.
(2)
又(e1-u12)(e2+u12)=(e2+u12)(e1-u12)=0.则
0=φ((e1-u12)∘(e2+u12))=φ(e1-u12)∘φ(e2+u12)=φ(e1)∘φ(u12)-φ(u12)∘φ(e2)-φ(u12)∘φ(u12).
从而由式(2),
φ(e1)φ(u12)+φ(u12)φ(e1)-φ(u12)φ(e2)-φ(e2)φ(u12)=0.
对上式分别左右同乘φ(e1)和φ(e2)可得:
φ(e1)φ(u12)φ(e1)=φ(e2)φ(u12)φ(e2)=0.
因此,
φ(u12)=φ(e1)φ(u12)φ(e1)+φ(e1)φ(u12)φ(e2)+φ(e2)φ(u12)φ(e1)+φ(e2)φ(u12)φ(e2)=
φ(e1)φ(u12)φ(e2)+φ(e2)φ(u12)φ(e1).
证毕.
引理3设uij,vij∈Uij(1≤i≤j≤2),则
(1)φ(u11∘v12)=φ(u11)∘φ(v12)且φ(u12∘v22)=φ(u12)∘φ(v22);
(2)φ(u11∘v11)=φ(u11)∘φ(v11)且φ(u22∘v22)=φ(u22)∘φ(v22).
证明(1)由于(u11-u11v12)(v12+e2)=(v12+e2)(u11-u11v12)=0.则由引理2和式(2)可得:
0=φ(u11-u11v12)∘φ(v12+e2)=φ(u11)∘φ(v12)-φ(u11v12)∘φ(e2)+φ(u11)∘φ(e2)-
φ(u11v12)∘φ(v12)=φ(u11)∘φ(v12)-φ(u11v12).
这说明
φ(u11∘v12)=φ(u11)∘φ(v12).
(3)
类似地,由(u12+e1)(v22-u12v22)=(v22-u12v22)(u12+e1)=0,我们有
φ(u12∘v22)=φ(u12)∘φ(v22).
(4)
(2)由式(3),一方面
φ((u11∘v11)∘v12)=φ(u11∘v11)∘φ(v12),
(5)
另一方面,我们有
φ((u11∘v11)∘v12)=φ(u11∘(v11v12))+φ(v11∘(u11v12))=φ(u11)∘φ(v11v12)+φ(v11)∘φ(u11v12)=
φ(u11)∘(φ(v11)∘φ(v12))+φ(v11)∘(φ(u11)∘φ(v12))=(φ(u11)∘φ(v11))∘φ(v12)+
2φ(u11)φ(v12)φ(v11)+2φ(v11)φ(v12)φ(u11).
由引理3知,φ(u11)φ(v12)φ(v11)=φ(v11)φ(v12)φ(u11)=0.从而由上式,
φ((u11∘v11)∘v12)=(φ(u11)∘φ(v11))∘φ(v12).
(6)
由式(5)和式(6),则对任意v12∈U12,有
(φ(u11∘v11)-φ(u11)∘φ(v11))∘φ(v12)=0.
(7)
由于φ是满射,则存在x∈U使得
φ(x)=φ(u11∘v11)-φ(u11)∘φ(v11).
(8)
从而由引理2可知,
φ(x)=φ(e1)φ(x)φ(e1)=φ(e1)φ(e1xe1)φ(e1)+φ(e1)φ(e1xe2)φ(e1)+
φ(e1)φ(e2xe2)φ(e1) =φ(e1)φ(e1xe1)φ(e1)=φ(x11),
其中x11=e1x1e1∈U11,于是由式(3)和式(7),
φ(x11v12)=φ(x11∘v12)=φ(x11)∘φ(v12)=φ(x)∘φ(v12)=0.
由于φ是单射,则x11U12={0},并由U12的忠实性得x11=0.从而φ(x)=φ(x11)=0,并由式(8)得
φ(u11∘v11)=φ(u11)∘φ(v11).
类似地,我们由式(4)可得φ(u22∘v22)=φ(u22)∘φ(v22).证毕.
定理1的证明由文献[4]的结论知,如果φ是Jordan同构,则φ保单位且条件(1),(2)和(3)之一成立.反过来,容易验证(1)⟹(3)和(2)⟹(3)分别成立.以下我们假设φ保单位且条件(3)成立.
设u,v∈U,则存在uij,vij∈Uij使得
u=u11+u12+u22,v=v11+v12+v22.
从而由引理3及φ(uii)∘φ(vjj)=φ(u12)∘φ(v12)=0(i≠j)可知,
φ(u∘v)=φ((u11+u12+u22)∘(v11+v12+v22))=φ(u11∘v11)+φ(u11∘v12)+φ(u12∘v11)+φ(u12∘v22)+φ(u22∘v12)+
φ(u22∘v22)=φ(u11)∘φ(v11)+φ(u11)∘φ(v12)+φ(u12)∘φ(v11)+φ(u12)∘φ(v22)+φ(u22)∘φ(v12)+
φ(u22)∘φ(v22)=(φ(u11)+φ(u12)+φ(u22))∘(φ(v11)+φ(v12)+φ(v22))=φ(u)∘φ(v).
因此,φ是Jordan同构.证毕.
设R是含单位的交换环,Mn×k(R)表示R上全体n×k矩阵.对n≥2且1≤m≤n,Mn(R)中形如
设B(H)表示复Hilbert空间H上全体有界线性算子构成的代数.H上的套N是B(H)中包含0和Ι且在强算子拓扑下闭的全序投影族,称
AlgN={T∈B(H):PTP=TP,P∈N}
为关于N的套代数.我们知道上三角矩阵代数与非平凡套代数均为三角代数,从而由[4]和[3]的结论以及定理1,我们有下列推论.

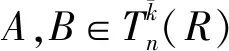
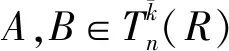
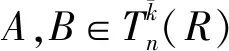
则φ要么是一个同构,要么是一个反同构.
推论2设N和M是复Hilbert空间H上的非平凡套,φ:AlgN→AlgM是一个线性双射且φ(Ι)=Ι,如果下列条件之一成立:
(1)φ(A∘B)=φ(A)∘φ(B),其中A,B∈AlgN满足AB=0,
(2)φ(A∘B)=φ(A)∘φ(B),其中A,B∈AlgN满足A∘B=0,
(3)φ(A∘B)=φ(A)∘φ(B),其中A,B∈AlgN满足AB=BA=0,
则存在可逆算子T∈B(H),使得对任意A∈AlgN有φ(A)=TAT-1或φ(A)=TJA*JT-1,其中J是共轭线性对合.
注1推论2在更弱的条件下得到了与文[14]相同的结论.文[17]证明了保单位且双边保Jordan零积的可加满射是双射,并由此给出了套代数上此类映射的具体结构,而推论2给出了套代数上保单位且单边保Jordan零积的线性双射的具体结构.

