路面不平度模型对车辆侧翻瞬态响应的影响分析

杨晨旭, 路永婕, 王美晨, 郑露峰

(1.石家庄铁道大学 机械工程学院,河北 石家庄 050043;2.石家庄铁道大学 省部共建交通工程结构力学行为与系统安全国家重点实验室,河北 石家庄 050043)

车辆侧翻是车辆瞬态失稳的一种情况,侧翻引发的伤亡率很高,根据美国公路交通安全管理局统计[1],2020年美国全年死于交通事故人数为38 824人,较2019年增长6.8%,其中由于车辆侧翻造成7 107人死亡,占总交通死亡人数的18.3%,较2019年增长13%。为了解决车辆的侧翻问题,学者们从道路线形优化、车辆结构设计和整车动力学等多个角度开展了研究工作。

金智林等[2-3]提出侧翻动态稳定因子的概念并在横向载荷转移率的基础上进行了关于侧翻2次预警研究;IMINE et al[4]考虑了车辆悬架的影响,建立了车辆侧翻模型;宋小文等[5]在考虑悬架和轮胎侧向变形的基础上改进了车辆的侧翻模型;朱天军等[6]在TTR算法基础上对侧翻预警进行改进,并验证了其可以有效地进行侧翻预警;石求军等[7]考虑车辆实际行驶时的挠动问题,提出了RBF-ADSMC算法,较传统SMC算法控制更能减少车辆侧倾角和侧向加速度的变化,提高车辆侧向稳定性。侧翻事故往往也与道路条件有关[8],一些学者也研究了路面激励下车辆行驶稳定性的情况。ELNASHAR et al[9]建立了汽车-道路耦合系统的时域控制微分方程组,研究了车速、路面表面特性和车体自身结构对系统响应的影响;覃凌云等[10]在考虑路面不平度情况下,得出了随着速度的增大,车辆负重轮动载荷与动载荷系数呈近似线性增大的结论;张韡等[11]探究了减速带对车辆平顺性的影响;鲍卫宁等[12]提出了一种既考虑路面不平度同时又可研究侧翻的新模型,得出转向越慢,路面对车辆侧倾角影响越明显的结论。上述文献通过车辆侧翻动力学模型、侧翻指标和不同路面激励对车辆侧翻的影响对车辆的瞬态失稳行为进行了大量研究。但是,大部分的侧翻响应分析都是基于传统的平整路面或者二维随机路面谱模型下进行的,对于各种路面谱激励下,尤其是三维路面不平度激励下的车辆瞬态响应特征研究还不足,而车辆瞬态响应的高精度计算对于改善车辆侧翻的事故率具有重要的意义。

建立了平整路面、二维路面和三维路面等3种不同类型的路面谱模型,综合考虑了双移线工况、鱼钩试验工况和角阶跃工况共3种经典侧翻工况,选取车辆横向载荷转移率、侧向加速度、横摆角速度和侧倾角曲线的时域变化描述车辆在侧向运动中的响应特征,对比了在平整路面、二维路面和三维路面激励下,对车辆瞬态响应变化的影响规律。

1 二维路面谱的构建

1.1 路面不平度功率谱密度

路面不平度可由路面功率谱密度描述其特性,当车辆纵向速度为u,车辆受到的激振频率为f,路面不平度可表示为[11]

(1)

式中,n0为空间频率参考值,n0=0.1 m-1;Gq(n0)为参考空间频率n0下的功率谱密度值。

路面等级可分为A～H 8个等级,选取常用的B级路面进行探究。根据文献[13],B级路面特性参数Gq(n0)几何平均值为6.4×10-5m3,σ2几何平均值为7.61×10-3m。

1.2 傅里叶逆变换法构建二维路面谱

基于傅里叶逆变换法构建二维路面谱基本过程为:利用路面功率谱密度求得傅里叶变换模值、利用随机序列构造出频域信号、通过傅里叶逆变换得到路面不平度序列[14]。其基本流程如图1所示。

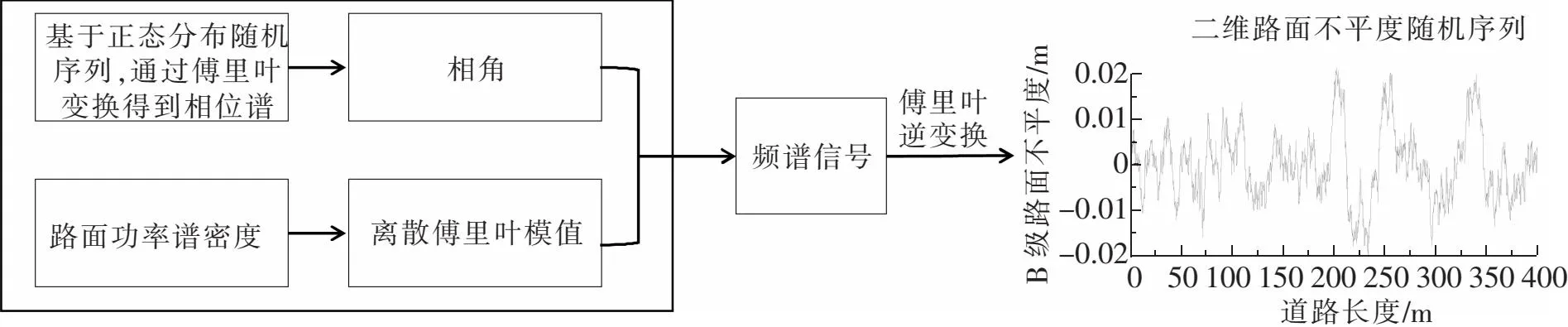
图1 二维路面谱建立流程图

傅里叶变换模值

(2)

式中,Gd(nk)为路面功率谱;N为采样点数;h为采样间隔;|X(k)|为傅里叶变换模值。

图2 B级二维路面不平度

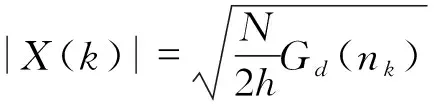
(3)

频域

|X(k)|=|X(k)|ejφk

(4)

式中,φk为相位角,k=0,1,2,…,N-1。

傅里叶变换

(5)

根据上述过程得到B级的二维路面随机激励曲线,如图2所示。

2 三维路面谱的构建

二维路面不能反映路面细节特征,仅能反映纵向上不平度激励,缺乏横向上不平度激励的描述。为了更加贴合实际,需要建立比较精确的三维路面谱。

2.1 基于结构函数法的分形维数确定

分形维数是分形理论中的一个重要参数。对于自相似图形来说,可将自身分成大小相等的N份,每一份的尺度为整体图形的1/r,分形维数D的求取,其相关表达式为[15]

D=lnr/ln(1/r)

(6)

结构函数法能够较好地求取二维路面的分形维数[16],可将路面不平度看作时间序列,其相关公式为

(7)

式中,r为两数值之间的间隔。

将S(r)与r用双对数坐标表示出来,再对其进行线性回归,斜率为幂指数W,此时分形维数D为

(8)

利用Matlab编程得到B级路面标准偏差为7.60,分形维数为1.51。

与国标中B级路面标准偏差进行对比,其数值偏差较小,体现构造二维路面的准确性较高。

2.2 基于正方形细分法的三维路面谱重构

因为二维路面的准确性较高,都具有很强的自相似特性,所以可进行三维路面谱的重构。

正方形细分法是在二维面上对正方形各节点进行高程差值,最终形成一系列三维空间随机点的一种方法[15]。应用该方法生成三维路面不平度,基本过程如图3所示。

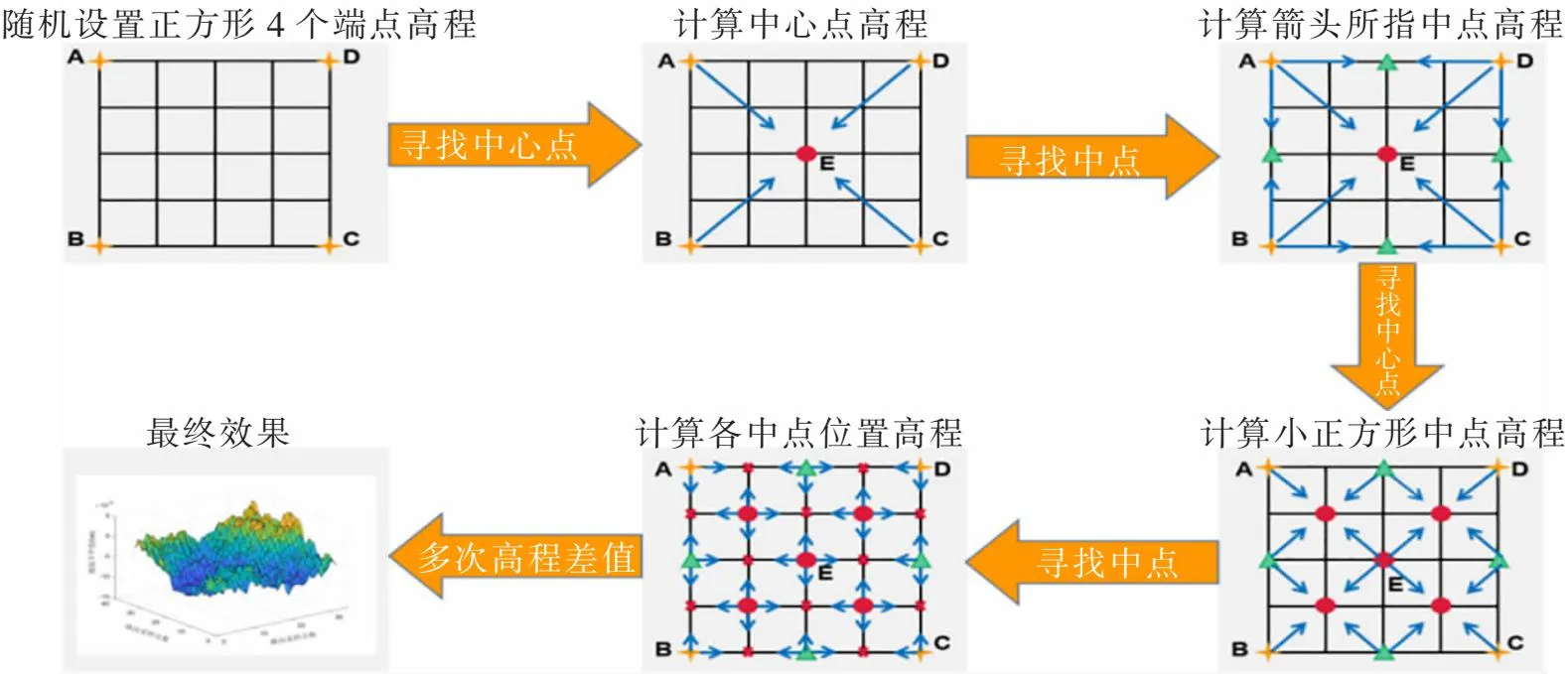
图3 正方形细分法基本过程

图3中中心点高程为所在正方形端点平均值与一个随机值叠加,中点高程为与其相邻两端点平均值与一个随机值的叠加。

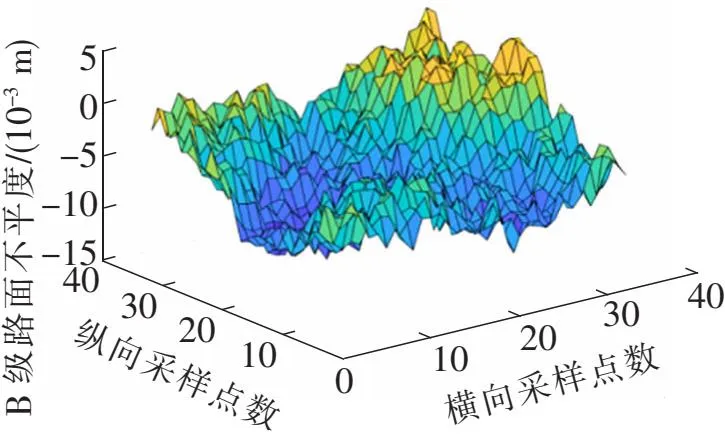
图4 B级路面三维路面图

其中,随机值可确定为

(9)

式中,H为分形参数,H=2-D,在此取分形维数D为1.51;gauss为符合正态分布的随机值;i为迭代次数;di为第i次相邻两点长度。

利用此方法可在二维路面模型基础上重构出B级三维路面,结果如图4所示。

2.3 三维路面重构结果的验证

因为重构的三维路面谱与实际路面是具有一些差别的,所以需要用频谱特性分析来验证路面谱的精确性。在B级三维路面上选取剖面二维曲线,从而得到二维路面不平度曲线,对二维路面谱进行频谱分析并与标准值进行对比,如图5所示。

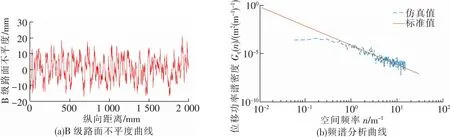
图5 B级路面不平度及频谱分析曲线

从图5可以看出,B级二维路面不平度曲线功率谱密度取值范围在标准值附近,可以验证重构的三维路面谱具有较高的精确性。

3 不同路面模型下侧向瞬态响应区别

三维路面建立后,可将路面信息导入到多体动力学软件中进行,并且在双移线、鱼钩工况和角阶跃典型工况下,对比分析不同路面不同平度模型下横向载荷转移率(LTR)、侧向加速度、横摆角速度和侧倾角4个瞬态响应。LTR表达式为

(10)

式中,Fzli为左侧轮胎的垂向载荷;Fzri为右侧轮胎的垂向载荷;n为总车轴的数目。

由式(10)可知,由于路面是不平稳的,[0～1]为LTR的范围;在其值为0时,左右两侧的垂向载荷之间的差值为0,说明汽车在平稳路面上行驶;在其值为1时,其全部载荷施加在一侧轮胎上,而另一侧并不会分担任何载荷,车辆发生侧翻。

选用B级路面进行仿真分析。其选取的车辆参数见表1。

表1 车辆参数

3.1 双移线工况

设置速度为36 km/h的双移线工况,不同路面模型激励时各响应的变化如图6所示。

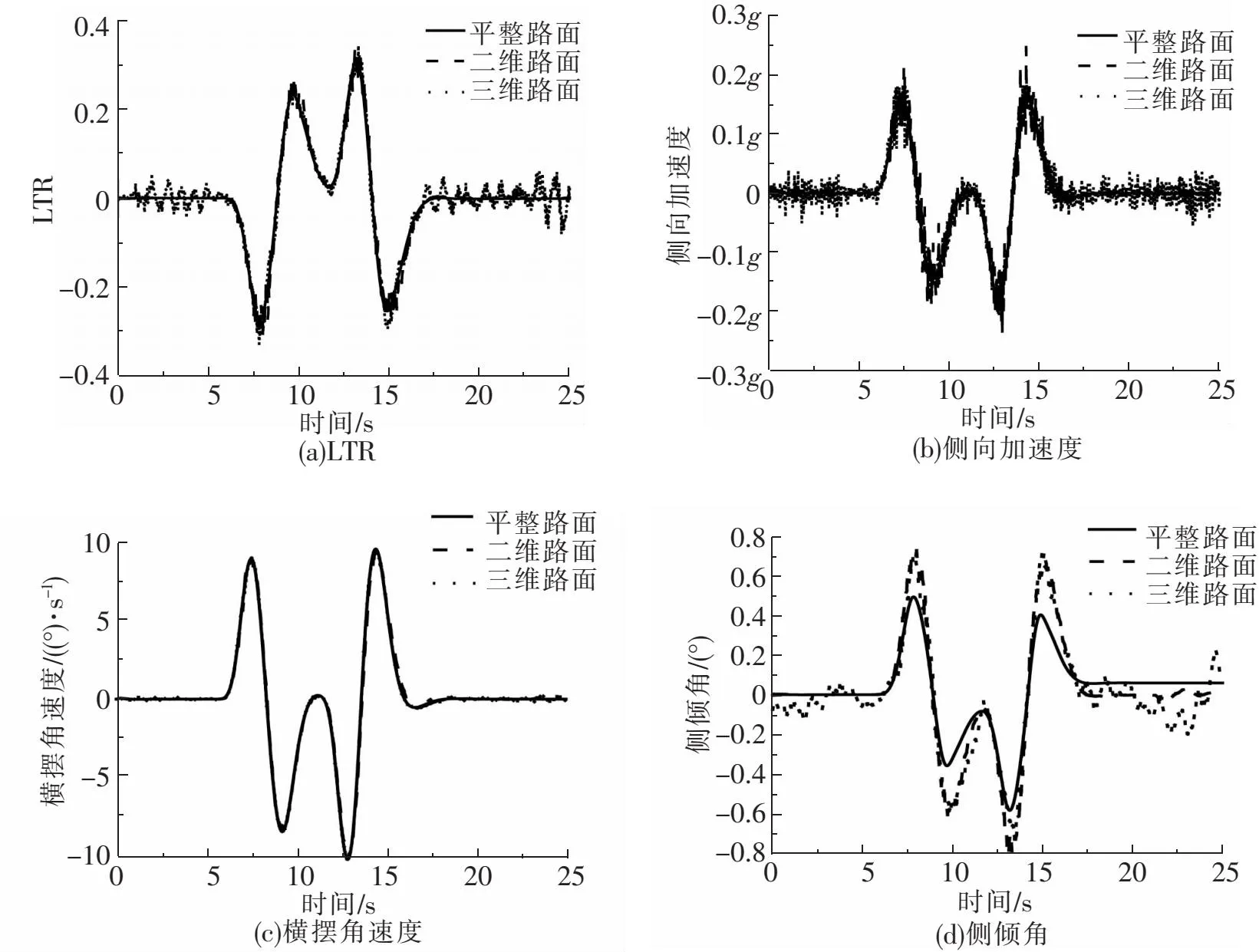
图6 不同路面模型下瞬态相应对比(双移线)

由图6(a)与图6(b)可知,车辆全程未发生侧翻,且在5 s时车辆开始侧向移动,在17 s时完成超车动作;0～5 s与17～25 s内,在三维路面下LTR在-0.080 5～0.027 0内波动,侧向加速度在-0.056g～0.038g内波动,二维路面和平整路面下LTR与侧向加速度的曲线平缓无波动,5～17 s内,三维与二维路面下车辆LTR与侧向加速度曲线都有波动,且三维路面与平整路面的LTR与侧向加速度波动最大差值分别为2.32%和0.019g。由图6(c)可知,3种路面模型下,对横摆角速度变化的影响无明显区别。由图6(d)可知,三维路面下,侧倾角最大为0.72°,最小为-0.68°,二维路面下最大值为0.73°,最小值为-0.68°,平整路面下其最大值为0.49°,最小值为-0.58°。与平整路面相比,二维路面与三维路面激励下,侧倾角最大值和最小值变化较大,且变化快。

3.2 鱼钩工况

设置鱼钩工况速度为60 km/h,方向盘转角1.3～1.7 s内由0°～200°变化,保持0.3 s后以同样速率降到-200°,不同路面模型激励时各参数的变化如图7所示。

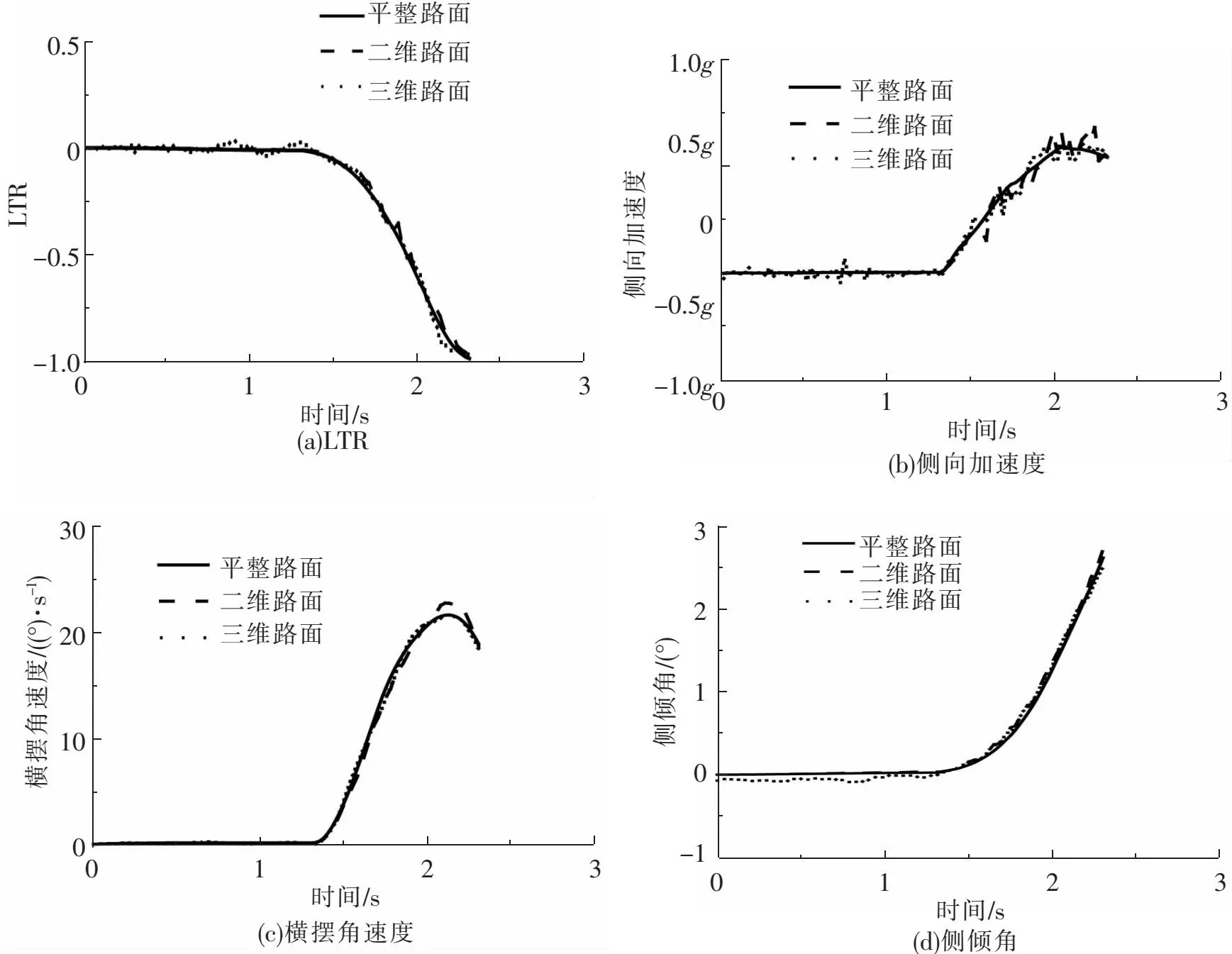
图7 不同路面模型下瞬态相应对比(鱼钩)

由图7(a)与图7(b)可知,车辆在1.5 s时开始转向,由于在2.3 s时LTR绝对值为1,故可判断车辆发生侧翻;0～1.5 s时,在三维路面下车辆LTR在-0.075 7～0.032 1内波动,侧向加速度在-0.046g～0.262g内波动,二维路面和平整路面下LTR与侧向加速度曲线平缓无波动;1.5～2.3 s内三维与二维路面下车辆LTR与侧向加速度曲线都有波动,且三维路面下波动最大,三维路面与二维路面的LTR与侧向加速度波动最大差值分别为0.124 4和0.118g。由图7(c)可知,3种路面模型下,横摆角速度变化无明显区别;由图7(d)可知, 2.3 s发生侧翻时,侧倾角无明显区别。

3.3 角阶跃工况

设置角阶跃工况的速度为80 km/h,方向盘在3 s时开始转向,3.8 s转到240°后保持不变,不同路面模型激励时各参数的变化如图8所示。

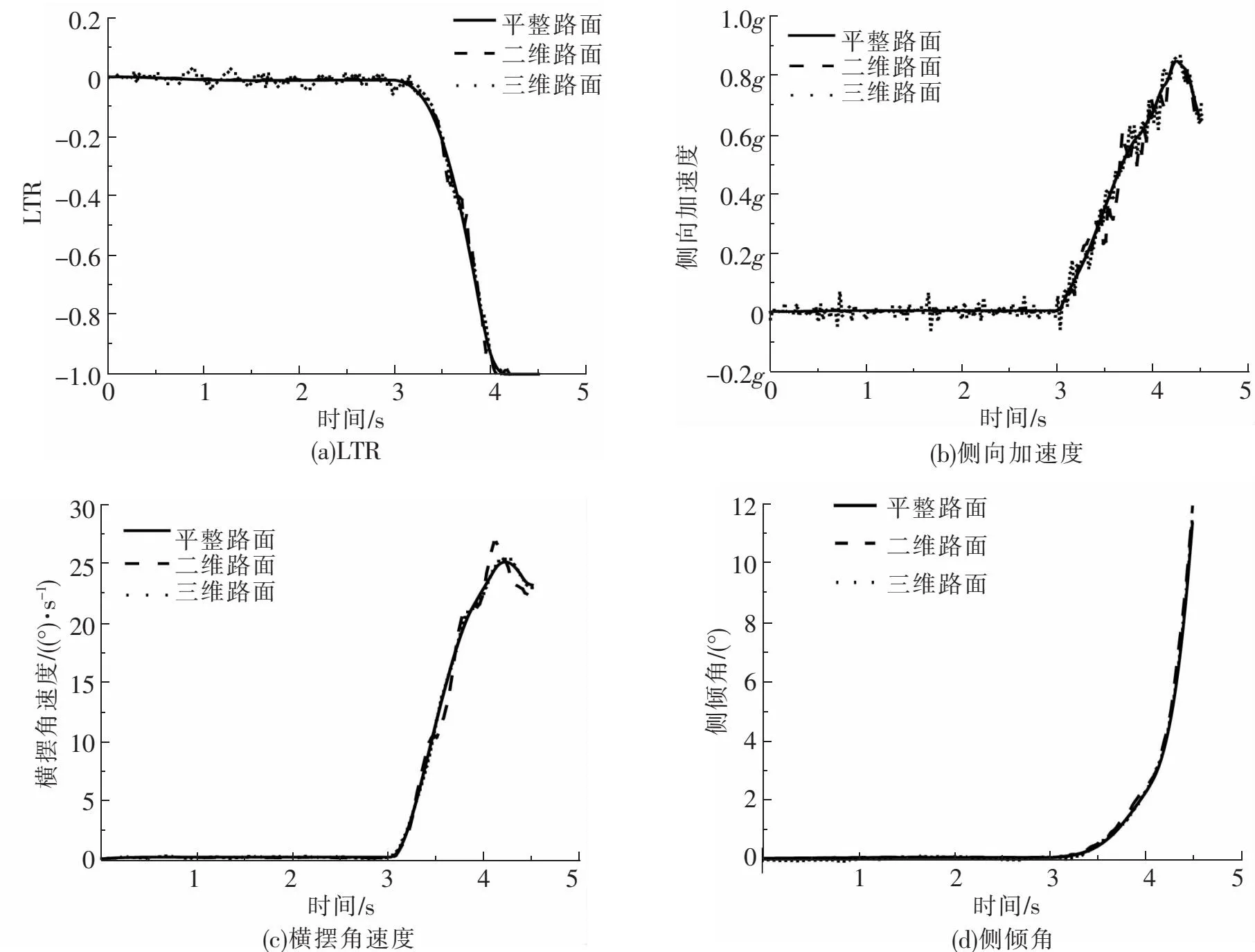
图8 不同路面模型下瞬态相应对比(角阶跃)

由图8(a)和图8(b)可知,车辆在3 s时开始转向,由于在4.1 s时LTR绝对值为1,故可判断车辆发生侧翻;0～3 s内,在三维路面下车辆LTR在-0.061 5～0.028 7内波动,侧向加速度在-0.046g～0.069g内波动,二维路面和平整路面下LTR与侧向加速度曲线平缓无波动;3～4.1 s内三维路面下LTR与侧向加速度曲线波动最大,三维路面与平整路面的LTR与侧向加速度波动最大差值分别为0.043 1和0.063g;由图8(c)与图8(d)可知,0～4.1 s内横摆角速度与侧倾角变化无明显区别。

4 结论

建立了平整路面、二维路面和三维路面模型,考虑了双移线工况、鱼钩工况和角阶跃工况,分别分析了LTR、侧向加速度、横摆角速度和侧倾角曲线时域的变化。得到如下结论:

车辆未转向时,三维路面模型下LTR、侧向加速度和侧倾角变化波动最大,平整路面与二维路面下其曲线无明显波动。车辆转向且未侧翻时,二维与三维路面下车辆LTR、侧向加速度和侧倾角曲线都有波动,且三维路面下波动最大;3种路面模型对横摆角速度变化影响无明显区别。车辆达到侧翻状态时,不同路面模型下LTR、侧向加速度、横摆角速度和侧倾角数值均达到侧翻阈值。