不同宽高比双边箱梁气动特性试验研究

张德旺, 王 欣, 杨 群, 刘小兵,2

(1. 石家庄铁道大学 土木工程学院,河北 石家庄 050043;2. 河北省风工程与风能利用工程技术创新中心,河北 石家庄 050043)

0 引言

对大跨度桥梁而言,风荷载在结构设计时往往起主要甚至决定性作用[1]。随着工程技术的不断发展以及交通量的持续增大,凭借着结构自重轻、施工方便、受力性能好等优点,双边箱梁在桥梁工程中得到较多使用[2-3],如已建成的宜宾盐坪坝大桥等。但因其具有明显的气动钝体外形,当空气流经主梁下侧时,会在下部空间内形成复杂的绕流,使得双边箱梁容易在低风速下发生涡激振动,造成结构的疲劳破坏[4]。为了提高结构的气动稳定性,确定更为安全的宽高比取值成为其结构抗风设计的关键问题之一。因此,有必要探究宽高比对双边箱梁气动特性的影响,从而为选取对结构安全最有利宽高比提供参考。

通过查阅现有文献可知,已有国内外学者针对不同宽高比断面主梁的气动特性进行了研究,研究对象主要为流线型扁平箱梁[5-8]和桁架梁[9]。关于双边箱梁气动特性方面的研究较少,如,王旭等[10]通过计算流体力学方法,在三维风场下研究了不同攻角时双边箱梁的气动三分力系数和流场机理,研究发现,双边箱梁下侧矩形区域的存在使其受到比其他类型梁更复杂的作用,因而稳定性较差,容易发生涡振;戴天帅[11]基于数值模拟方法,与风洞试验结果对照,研究了2种常见的迎风端流线型对双边箱梁静力三分力系数的影响,结果表明,双边箱梁迎风端的流线型程度对阻力系数影响较明显,对升力和升力矩系数影响较弱。可以看出,目前关于双边箱梁气动特性研究的对象主要为固定宽高比梁,对于不同宽高比双边箱梁的气动特性研究较为缺乏。

鉴于以上分析,以某跨海大桥的双边箱梁为研究背景,通过节段模型风洞测力、测压试验来研究不同宽高比双边箱梁的气动力特性、风压分布特性和旋涡脱落特性随风攻角的变化规律,并通过各宽高比模型表面的风压分布特性来解释其气动力系数的变化规律,从而为该类型主梁的实际工程提供参考。

1 试验概况

1.1 工程概况

以某跨海大桥为实际工程背景,如图1所示,该大桥为双塔三跨式斜拉桥,跨径组成为(137.2+324.4+137.2) m=598.8 m,索塔高度为85.1 m。图2所示为该桥主跨的主梁断面形式,该主梁为双索面体系的钢筋混凝土双边箱梁,宽度为17 300 mm,不考虑防撞护栏高度为2 550 mm,宽高比约为6.78。

图1 大桥总体布置图(单位:m)

图2 双边箱梁断面形式(单位:mm)

图3 测力测压试验模型安装

1.2 试验模型与工况

试验在石家庄铁道大学风工程研究中心边界层风洞实验室的高速试验段中进行,该试验段宽2.2 m,高2.0 m,长5.0 m,最大风速可达80.0 m/s,紊流度不超过0.2%。为满足阻塞度不超过5.0%的要求,按照缩尺比1∶30制作该双边箱梁的试验模型。试验模型安装见图3,试验模型采用木质结构,并在模型中部设置通长的钢管,以便固定在两边的测力天平上,在节段模型左右两端设置矩形端板以保证试验的二元性。通过调节两侧测力天平上螺丝的松紧来控制模型围绕钢管轴心的旋转角度,调节来流风攻角。

图4 不同宽高比模型的断面形式及测点布置(单位:mm)

为研究宽高比(即B/D,其中,B和D分别为双边箱梁断面的宽度和高度)对双边箱梁气动特性的影响,对实际工程中的抗风设计提供参考,在实际工程中常见的宽高比范围内选取了3个宽高比5.00、6.78、9.00进行试验,其中6.78为研究中实桥的宽高比。如图4所示,除宽高比为9.00的模型以外,其余2种宽高比的双边箱梁模型均以宽高比为9.00的模型为主体,通过增加补偿段的方法来改变模型的宽高比。此外,对各宽高比模型均设置了从-5°到5°的不同风攻角,变化步长为1°,以研究不同风攻角时宽高比对双边箱梁气动特性的影响。

研究采用刚体模型风洞测压试验与测力试验同步进行的方式来开展。在刚体模型测压试验方面,如图4所示,针对不同宽高比的双边箱梁模型,在模型中部横截面的外缘布置了一圈风压测点,以测量模型表面风压。由于模型表面拐角处的风压变化较为剧烈,因此对拐角附近的测点进行了适当加密。防撞护栏处圆形扶手与下部支座相连接的部分在纵向间隔布置,且圆形扶手尺寸太小,因此没有对这两处布置风压测点。宽高比取值为5.00、6.78和9.00的双边箱梁模型表面风压测点数目分别为124、118和106个。测压试验采用美国Pressure Systems公司生产的DTC系列微型ESP压力扫描阀和DTC Initium数据采集系统对测点处的风压信息进行采集,采样频率为330 Hz,采样时间为30 s。在刚体模型测力试验方面,该双边箱梁模型的两端会被安装在六分量高频测力天平上,从而采集模型整体所受的气动三分力时程信息,该测力设备由美国ATI公司生产,采样频率为1 500 Hz。

1.3 参数定义与可靠性验证

如图5所示,黑色箭头指示模型所受来流风的方向,U∞为模型远前方的来流风速,风攻角用α表示,FD、FL和M分别为风轴坐标系下由测压或测力试验所得到的模型单位长度上的阻力、升力和扭矩。为了表述方便,图5中模型断面的各个角点均用小写英文字母来表示,例如:a点、d点、h点。

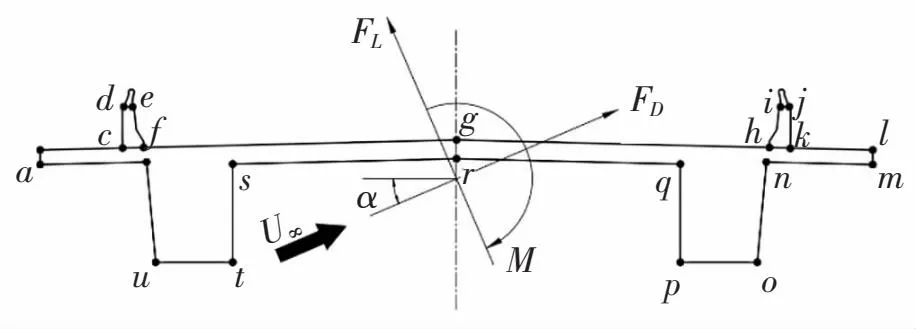
图5 风攻角及三分力系数定义

可采用无量纲风压系数Cp来描述模型表面的风压分布情况,定义为

(1)

式中,Pi为模型表面测点总压;Ps为参考点处的静压;ρ为空气密度。

三分力系数定义如下

(2)

(3)

(4)

各宽高比双边箱梁在不同风攻角下的旋涡脱落特性可用无量纲参数斯托罗哈数表示,定义如下

(5)

式中,f为旋涡脱落频率。

图6给出了宽高比为6.78的双边箱梁模型的测压试验与测力试验结果对比。可以发现,2种试验方法得到的升力系数和扭矩系数十分接近,而阻力系数的测压试验结果稍小于测力试验结果。造成该差异的原因可能有2方面原因:①防撞护栏处圆形扶手及其与下部支座相连接的部分没有布置风压测点,测压试验结果无法考虑这两部分的风阻力;②测压试验无法获取来流在模型表面产生的摩擦力。

图6 宽高比为6.78的双边箱梁模型测力试验和测压试验结果对比

2 试验结果讨论与分析

2.1 气动力特性

图7(a)为不同宽高比双边箱梁阻力系数随风攻角的变化规律。当-5°≤α≤-2°时,随着双边箱梁宽高比的增大,阻力系数先增大后减小,变化幅度较大。当-1°<α≤2°时,随着宽高比的增大,阻力系数表现为先减小后增大的趋势。当2°<α≤5°时,随着宽高比的增大,阻力系数迅速增大,受宽高比变化的影响明显。随风攻角增大,宽高比为5.00和6.78时,双边箱梁的阻力系数先减小后缓慢增大,B/D=9.00时阻力系数在小范围内发生波动。

图7(b)为不同宽高比双边箱梁升力系数随风攻角的变化规律。当-5°≤α<0°时,随着宽高比增大,向上的升力迅速减小,并逐步变为更大的、向下的升力。当0°≤α<3°时,随着宽高比由5.00增大到6.78,较大的升力迅速变为较小的、向下的升力,宽高比为6.78和9时升力系数则较为接近。当3°≤α≤5°时,随着宽高比增大,向上的升力由0附近增大到较大的值。当B/D=5.00,-5°≤α≤2°时向上的升力缓慢增大,并当攻角由2°增加到3°时,骤减到0左右。当B/D=6.78时,负攻角时的升力向下且值较小,随着正攻角的增大升力方向由下变上。当B/D=9.00时,随风攻角的增大,向下的升力由大变小,并当α=3°时减为0,随后由0变为向上的、较大的升力。

图7(c)为不同宽高比双边箱梁扭矩系数随风攻角的变化规律。随着宽高比的增大,扭矩系数均逐渐减小,且其变化幅度随着攻角由-5°变为5°逐渐减小。在较大的负攻角时双边箱梁的扭矩受宽高比变化影响最大,顺时针的扭矩随宽高比的增大迅速减小并变为逆时针方向。当B/D=5.00时,扭矩系数先缓慢增大后逐渐减小;当B/D=6.78时,扭矩系数随攻角的变化较为平缓;当B/D=9.00时,随风攻角由-5°变化到5°,扭矩由逆时针方向变为顺时针方向,且顺时针的扭矩逐渐增大。

图7 不同宽高比双边箱梁气动三分力系数随风攻角变化规律

2.2 风压分布特性

鉴于大攻角时气动力系数变化明显,有必要对大攻角下双边箱梁气动力系数随宽高比的变化机理做出进一步解释,下面将通过研究双边箱梁的表面风压分布特性初步探讨气动力系数的变化机理。

图8为α=-5°时不同宽高比双边箱梁表面的风压系数分布情况。从阻力系数变化来看,当宽高比由5.00增大到6.78时,c-d面风压由较小的负压变为正压,h-i面负压存在小幅减小,均对阻力系数的增大存在正贡献;e-f面上负压存在小范围的减小,且u-v面上正压逐渐减小,对于阻力系数的增大存在负贡献。因为c-d面上的风压变化与u-v面相比较为显著,因此当宽高比由5.00增大到6.78时阻力系数增大。当宽高比由6.78增大到9.00时,c-d面上正压增大的幅度与j-k面上负压减小的幅度较为接近,它们对阻力系数变化存在相反的贡献,因而相互抵消,但e-f面、l-m面、n-o面上负压的明显减小,以及u-v面上正压迅速减小并出现一定范围的负压,均使得阻力系数明显减小。

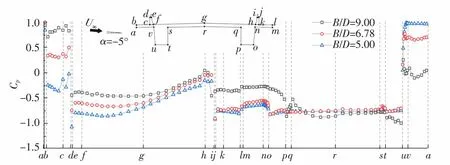
图8 α=-5°时不同宽高比双边箱梁表面风压系数分布

从升力系数的变化来看,随着宽高比的增大,b-c面上的风压由负压变为正压并迅速增大,d-e面、f-g面、g-h面上的负压均存在一定幅度的减小,v-a面上的正压减小并出现一定范围的负压,这些均对升力系数的减小存在正贡献,k-l面、m-n面上风压的变化相似但方向相反,可近似抵消,因此升力系数值迅速减小,升力方向发生变化。

图9为α=5°时不同宽高比双边箱梁表面的风压系数分布情况。对阻力系数而言,随着宽高比增大,a-b面上的正压逐渐增大,c-d面、p-q面上的负压逐渐减小,均对阻力系数的增大起到正贡献,且p-q面上负压减小对阻力系数的增大所带来的正贡献大于s-t面上负压减小所带来的负贡献,使得阻力系数随宽高比增大而明显增大。对于升力系数而言,随着宽高比的增大,q-r面、r-s面和t-u面的负压均有所减小,对升力系数的增大起到正贡献,而b-c面上负压减小对升力系数的增大起到负贡献,使得升力系数有所增大。

图9 α=5°时不同宽高比双边箱梁表面风压系数分布

可以发现,随着宽高比由5.00增大到6.78,关于对阻力系数变化起正贡献的作用面数量与起负贡献作用面数量的差值,α=5°时的差值大于α=-5°时,因此,较大的正攻角对阻力系数的影响大于较大的负攻角。当α=-5°时,对升力系数的变化起到正贡献的作用面数量和有效宽度均超过α=5°时的情况,因此,较大的负攻角对升力系数的影响明显大于较大的正攻角。

2.3 旋涡脱落特性

对3种宽高比双边箱梁在不同风攻角时的升力系数时程进行快速傅里叶变换(FFT)可以得到如图10～图12所示的傅里叶幅值谱图,图10～图12中,AF表示傅里叶幅值。

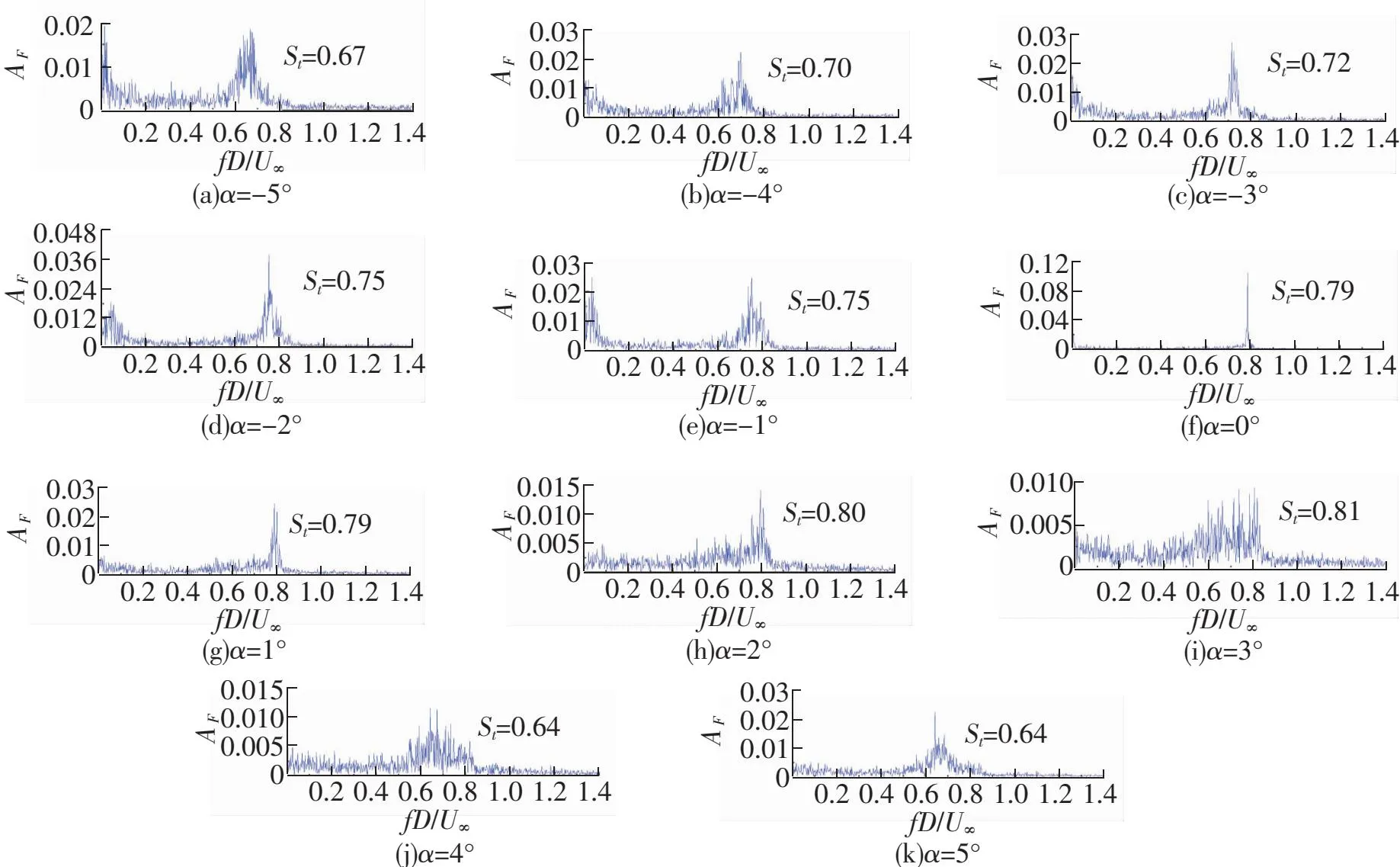
图11 B/D=6.78时双边箱梁不同风攻角下升力系数的傅里叶幅值谱图

图12 B/D=9.00时双边箱梁不同风攻角下升力系数的傅里叶幅值谱图

从图10～图12可以看出,当B/D=5.00时,随着风攻角由-5°变为5°,斯托罗哈数先逐渐增大后缓慢减小,并在α=1°时取得极大值0.66;当B/D=6.78时,随着风攻角由-5°变为5°,斯托罗哈数先逐渐增大后迅速减小,并在α=3°时取得极大值0.81。当B/D=9.00时,随着风攻角由-4°变化到4°,斯托罗哈数先小幅增大,而后基本稳定在0.8左右。当B/D=5.00时,斯托罗哈数的值一般在0.48和0.66之间,当B/D=6.78时,该值一般在0.64和0.81之间,当B/D=9.00时,一般在0.8附近,因此,斯托罗哈数随着宽高比的增大而逐渐增大。

在小攻角时,不同宽高比双边箱梁升力系数的傅里叶幅值谱图上均存在明显的峰值,即不同宽高比双边箱梁在小攻角时均存在明显的旋涡脱落现象。大攻角时,随着双边箱梁宽高比的增大,幅值谱图上的峰值愈发不明显,这说明在大攻角时旋涡脱落现象随着宽高比的增大而逐渐变得不明显。

3 结论

(1)宽高比对双边箱梁阻力系数的影响主要体现在较大的正攻角。随着宽高比的增大,阻力系数逐渐增大。

(2)宽高比对双边箱梁升力系数和扭矩系数的影响主要体现在较大的负攻角。随着宽高比的增大,向上的升力逐渐减小,并变为向下的升力;顺时针的扭矩逐渐减小,并变为逆时针的扭矩。

(3)小攻角下,不同宽高比的双边箱梁均存在明显的旋涡脱落现象,且随着宽高比的增大,斯托罗哈数逐渐增大。大攻角下,随着宽高比的增大,双边箱梁的旋涡脱落现象逐渐变得不明显。