缩比火箭发动机尾焰等离子特性研究

李心阳，王大锐，任牧原，王业军，连 欢

（1.高温气体动力学国家重点实验室，中国科学院力学研究所，北京，100190；2.中国科学院大学，北京，100190；3.北京宇航系统工程研究所，北京，100076）

0 引言

在低空环境下，运载火箭不可避免地与低空荷电的云层发生近场或远场相互作用，由此可带来诸多飞行安全隐患。其中较为突出的便是由火箭本体以及发动机尾喷流与云层间的电磁作用所导致的诱导电流甚至诱导闪电的问题［1］。火箭以超声速在大气层内飞行时，火箭尾焰与环境空气间相互作用，致使尾喷流具有强瞬态、强湍流和高度非线性耦合的特点，呈现出燃烧及电离反应、激波、膨胀波、湍流漩涡、流动分离、边界层分离等多尺度、多物理场耦合共存的复杂流场结构［2］。上述强非定常和非均匀流场意味着分离体受到多重因素耦合作用下的复杂不稳定气动力，影响飞行的稳定性。由此可知，正确理解火箭低空飞行过程中尾部喷流反应流场以及电磁特性，即火箭发动机尾焰等离子特性，是揭示火箭尾焰与荷电云层以及低空稠密大气间气动力/热以及电磁作用机制的基础，对于在低空大气层飞行环境中实现安全、可靠的火箭发射具有一定参考价值。

碱金属热电离产生的离子、自由电子和燃烧化学反应产生的较少量带电离子以及自由电子是尾焰弱电离流场内带电粒子的主要来源［3］。数值模拟方面，主要通过对流场以及燃烧化学反应的仿真得到温度、压强、主要组分浓度等反应流场参数，从而进一步计算出电导率等电磁特性参数，尚需与试验结果进行详细比对［4-7］。试验方面，可以通过对飞行状态下尾喷焰的温度及主要燃烧产物进行测量，基于传统的电磁学理论推断尾焰喷流中等离子体的浓度范围并计算其电导率和相对介电常数等电磁特性［8］，然而飞行试验测得的数据以定性观察为主，无法进行准确的定量分析。地面试验可采用朗缪尔探针测量技术［9］，或者基于微波透射的方法间接测量离子密度等主要火箭发动机尾焰等离子体电磁参数［10］。由于火箭发动机尾焰喷流对于微波的衰减是复杂的物理、化学过程，通过微波透射方法测量等离子体浓度需要引入诸多假设，通常采用测量原理较为清晰明确的朗缪尔探针测量方法［11-15］。

综上，为理解缩比火箭发动机尾焰等离子体特性，需要分别阐明缩比火箭发动机尾焰燃烧组分特征以及尾焰弱电离流场特性。本文首先开展火箭尾焰流场的自发辐射光谱测量，获得了尾焰流场反应流场的主要燃烧特征组分；然后基于朗缪尔探针测量技术获得离子密度、电子密度和电子温度等主要火箭发动机尾焰等离子体电磁参数；最后，给出火箭发动机尾焰电导率轴向分布特性，说明与尾焰电磁特性的相关性较强的弱电离气体流场结构。

1 试验方法

1.1 自发辐射光谱光纤传感器

自发辐射光谱光纤传感器主要用于对光轴方向上燃烧产生的光信号进行径向积分，采集并耦合进多模光纤并传送至光电传感器进行光信号强度测量，本文所使用的自发辐射光谱传感测量系统在设计中采用了基于几何光线追迹模拟与物理光场追迹仿真的交互迭代设计方法，光学上采用单片小数值孔径结构，配合1 000 μm大孔径多模光纤，该准直器可实现对物距50～8 000 mm 范围内95%以上的轴上光信号进行光纤耦合，波长范围为200～1 500 nm。考虑到超高速高温气流冲刷的使用环境，镜片采用高硬度蓝宝石材料，设计中重点优化了系统的温度容差性以及热密封特性。

1.2 朗缪尔探针测量

朗缪尔探针测量是真空环境中测量等离子体特性的常用技术手段，由于应用于朗缪尔探针的等离子体理论模型参数存在海平面压力适用性问题，选择朗缪尔双探针、三探针联合试验方法，实现尾焰电导率测量。

1.2.1 朗缪尔双探针测量原理

朗缪尔双探针通过施加扫频电压，可以得到电压与电流之间的对应关系曲线，典型的双探针伏安特性曲线如图1所示。

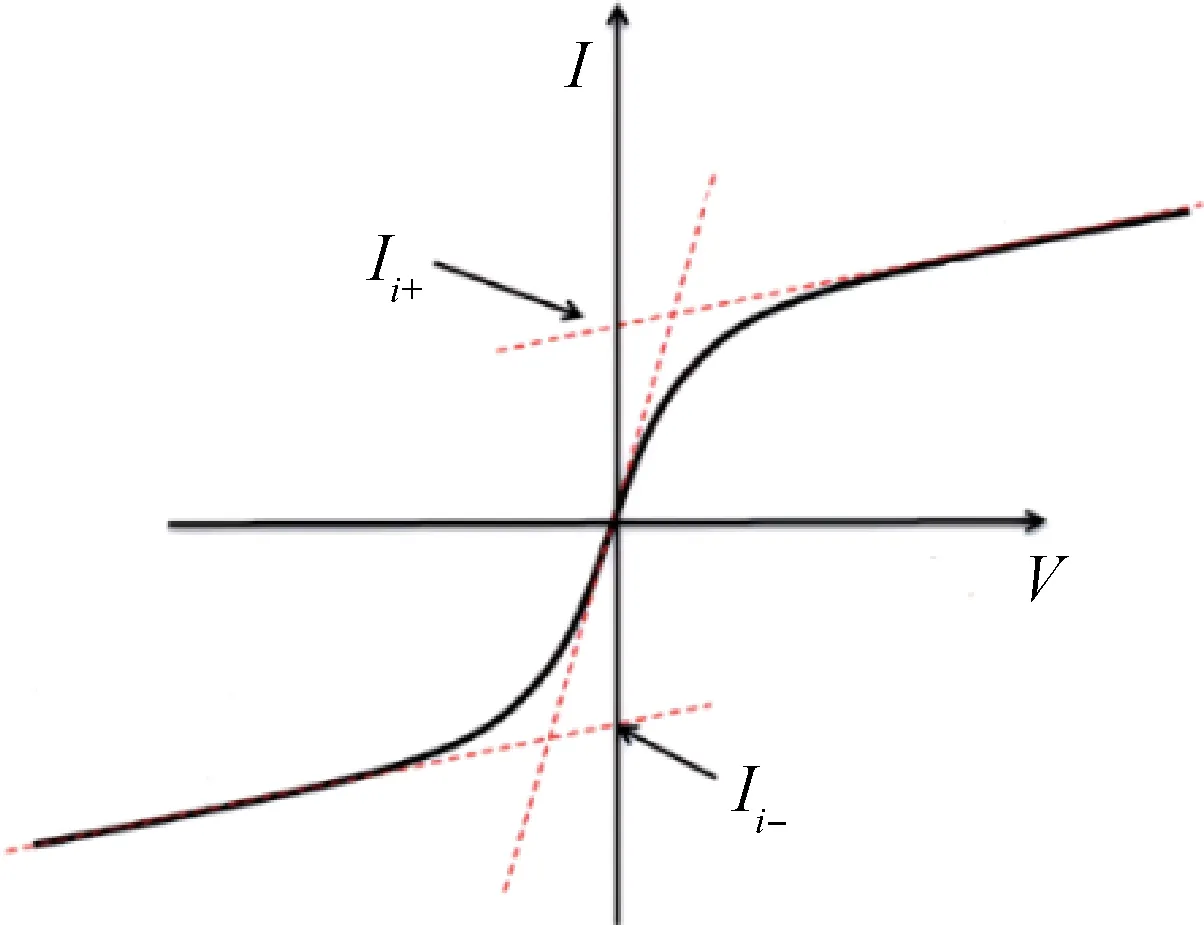
图1 朗缪尔双探针典型伏安特性曲线Fig.1 The typical V-I characteristic curve of a Langerhans dualprobe

根据扫描电压与探针电流的关系可计算离子密度、电子温度等参数［16］。在离子饱和区域对探针电流进行一次线性拟合，得到离子饱和电流Ii，测量值ID与饱和电流之间的关系为

式中e为电荷量；k为玻尔兹曼常数；Te为电子温度；VD为测量电压。求导可得电流测量值和离子电流之间的关系式：

电子温度可以由电压为0时的伏安特性曲线斜率求出：

进一步由离子饱和电流计算离子密度：

式中Ap为探针表面积；mi为离子质量。

1.2.2 朗缪尔三探针测量原理

三探针的计算方法与双探针类似，不同的是三探针结构无须施加扫频电压，根据电路结构不同又进一步分为电压模式和电流模式。图2为两种模式的简化电路模型。

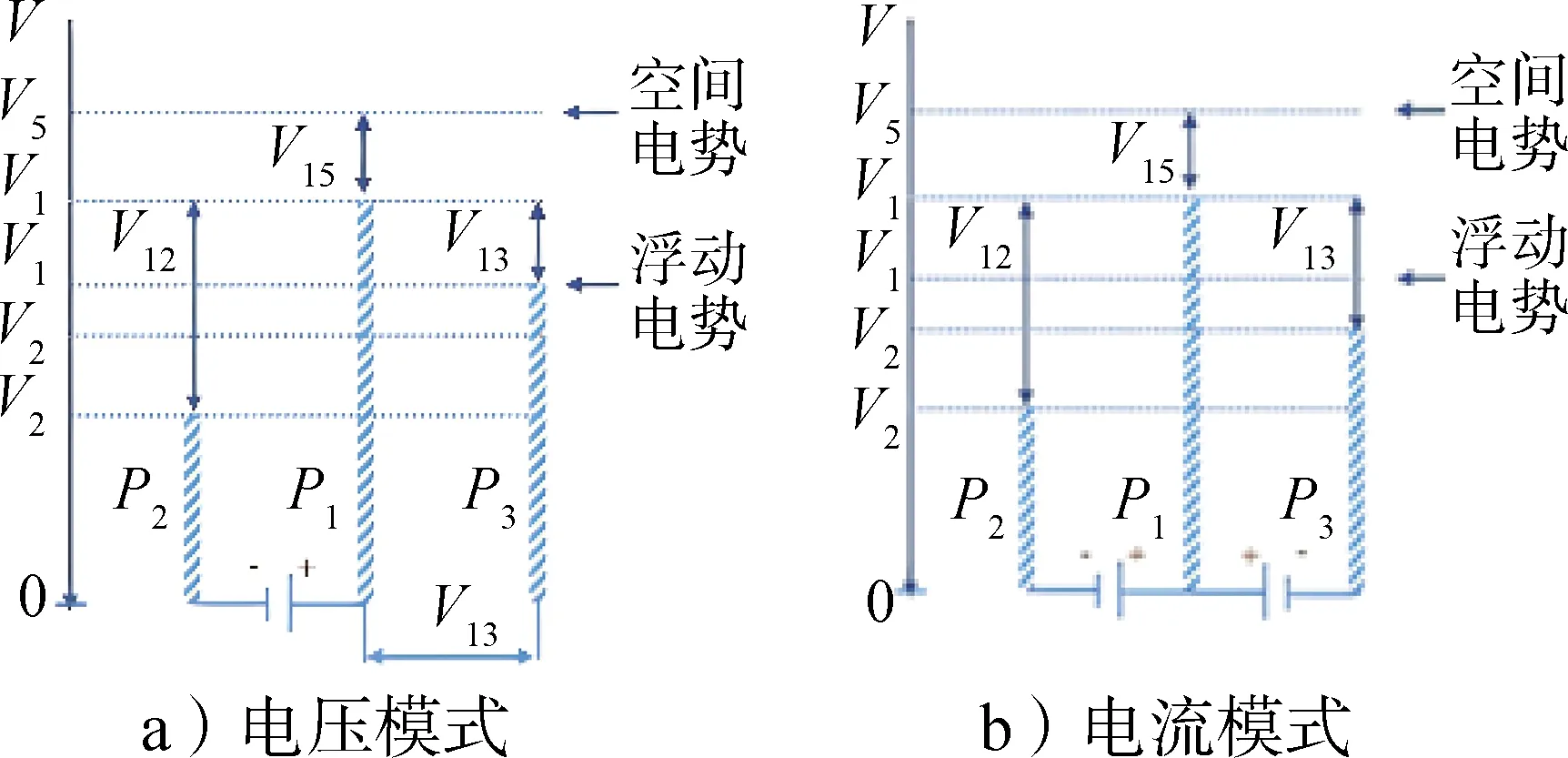
图2 三探针简化电路模型Fig.2 The simplified circuit model diagram of a three-probe setup

本次试验采用的是电压模式的电路结构，通过联合求解式（5）、式（6）可以计算出离子密度、电子密度（由于鞘层内等离子仍近似满足电中性条件，并且在此温度下认为正离子只携带一个正电荷，因此可以认为电子密度与离子密度相等）和电子温度：

式中V13为1、3 探针间电势差；V12为1、2 探针间电势差；ne为电子密度；A为探针表面积，通常认为3个探针表面积相等。

1.3 高精度伺服平台

与微波试验方法相比，朗缪尔探针具有更高的时间分辨率，但仅能完成单点测量，如果要获得整体的更多数据，就需要在等离子体内不同位置设置多个测点。因此本文的研究中，设计了一种伺服驱动平台获得了双探针以及三探针在轴向10 个测量点位的等离子体分布特性。每个测点采样时间为1 s，双探针加载-20 V～+20 V扫频电压，1 s内扫描10次，采样频率10 Hz，三探针加载40 V的偏置电压可实现连续采样，采样频率设置为1 MHz。

本次试验设计的专用高精度伺服驱动平台，同时搭载朗缪尔双探针和三探针，朗缪尔双探针和三探针安装在固定于伺服平台的大臂上，具有相同的轴向坐标，径向坐标有20 mm的差异，通过精确控制伺服平台的占空比实现火箭尾焰等离子体不同轴向测量点位的等离子体特性测量。直线运动模块运动受力示意如图3所示，运动模块组成如图4所示。

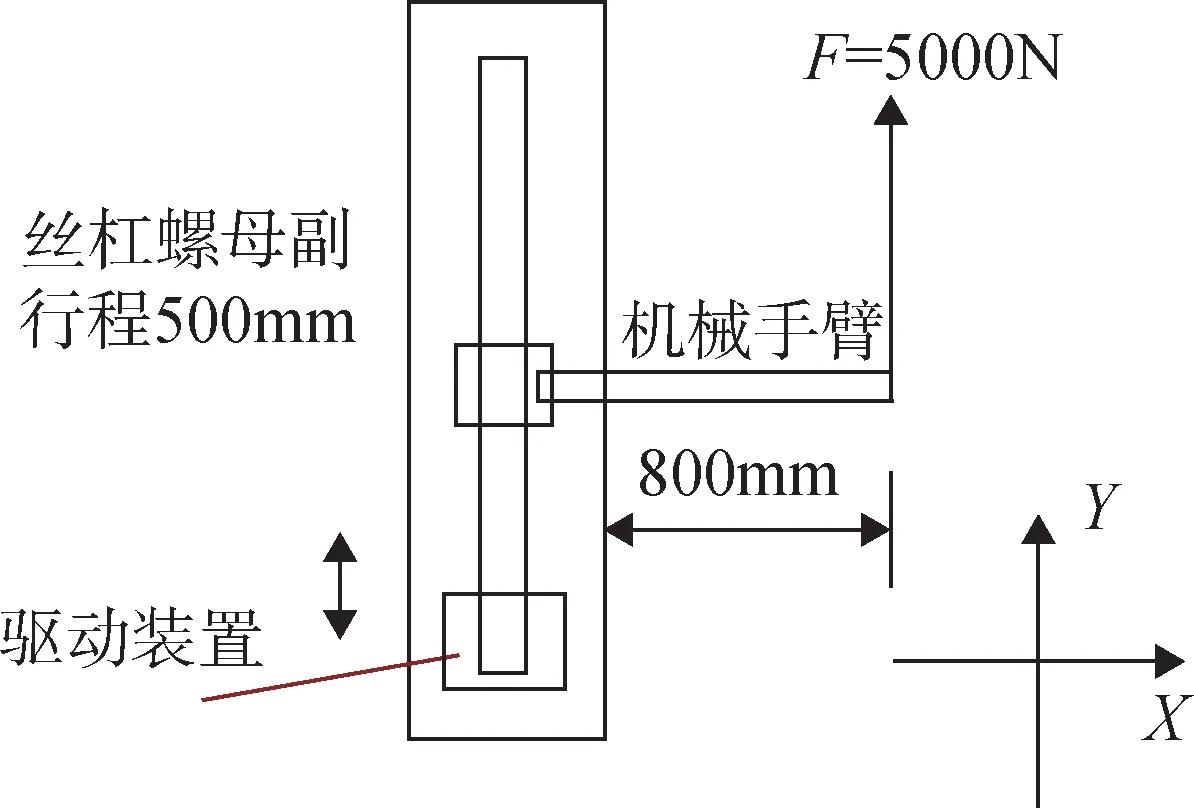
图3 直线运动模块运动受力示意Fig.3 Force analysis of the linear movement module

图4 直线运动模块组成示意Fig.4 Illustration of the linear movement module

如图3 所示，Y方向的运动行程共500 mm，触发开始信号后开始匀速运动1 s，移动50 mm后停止1 s，再运动1 s，移动50 mm 后再停止1 s，重复直至完成500 mm 总行程时运动自动停止。运动和停止过程中整个直线运动模块和机械手臂可承受Y方向5 000 N的力，力臂长度为800 mm。

2 试验结果处理与分析

2.1 自发辐射光谱测量结果

火箭尾焰流场自发辐射220～1 100 nm波段光谱如图5所示。

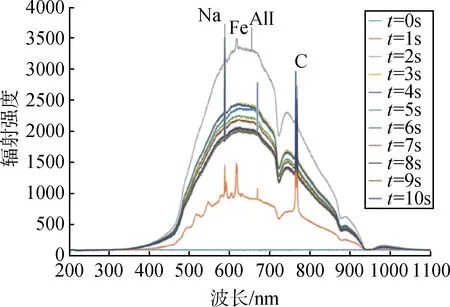
图5 火箭尾焰流场自发辐射220～1100nm波段光谱Fig.5 Chemiluminescence between 220～1100nm

在试车中选择10 s稳定燃烧区间，由于火箭尾喷管安装有伺服作动机构，10 s内测量的火箭尾焰流场自发辐射强度存在一定变化，由图5 可知存在4 个主要的特征峰，对应波段分别是588 nm、619 nm、669 nm、765 nm，且特征峰对应波段不随自发辐射强度变化而偏移，说明所观测的4个光谱特征峰稳定存在。根据标准光谱数据库，这4 个特征峰分别对应Na、Fe、Al、C 元素，其中Na、Fe、Al 碱金属元素对电导率有突出贡献，碱金属元素分别主要来源于大气中含盐成分、合金结构材料以及推进剂燃烧。

2.2 火箭尾焰流场电导率的轴向分布

缩比火箭尾焰流场的二维红外成像如图6所示。

图6 红外温度场分布特性Fig.6 Distribution characteristics of infrared temperature field

根据红外图像提供的温度数据可以代入公式计算出相应的电导率［17］：

式中σi为电导率；Vm为离子碰撞频率；n为中性粒子密度；Ai为粒子碰撞截面面积；vi为粒子热运动速度；Ti为离子温度，与气体温度相同；p为气体压力，取常压；T为气体温度。

设定离子质量为10 g/mol，平均温度为800 K，计算得电导率为2.8×10-3S/m，双探针电导率范围为10-4～10-3S/m 之间，相同条件计算得到的三探针电导率数量级在10-5～10-4S/m，结果如图7～图8所示。

图7 双探针电导率轴向分布Fig.7 Axial distribution of conductivity with double-probe setup

图8 三探针电导率轴向分布Fig.8 Axial distribution of conductivity with three-probe setup

两种探针测算到的电导率数值范围存在差异，测量差异可能主要由于朗缪尔双探针安装于中心轴线，而朗缪尔三探针径向分布安装，体现了电导率沿径向分布衰减的特性。需要说明的是，对于火箭尾焰这种构成复杂的弱电离气体，基于传统等离子体鞘层理论的探针测量原理可能不完全适用，测量结果仍然会存在一定误差，而当前尚未见关于修正的探针鞘层理论方法的相关研究。两种探针总体沿轴向分布趋势类似，即随着轴向距离的增加，电导率分布呈指数减小。应当说明的是，上游靠近喷口测量点附近电导率有一短暂的上升阶段，对应发动机建立稳定工作推力过程。

2.3 朗缪尔双探针离子密度的概率密度分布

利用核密度估计函数分别计算10 个测点处朗缪尔双探针测量得到的离子密度的概率密度分布，结果如图9所示。

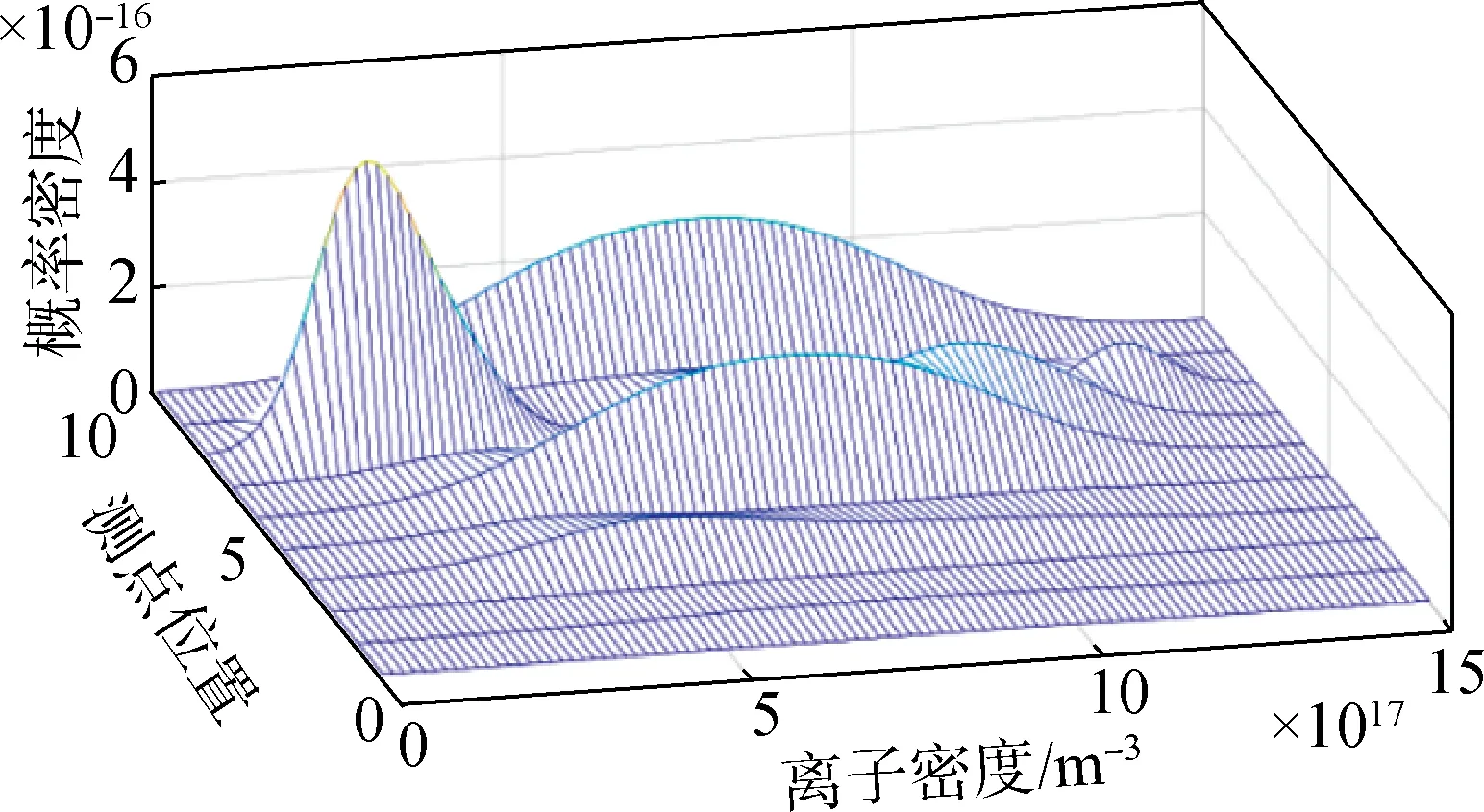
图9 朗缪尔双探针离子密度的概率密度分布Fig.9 Probability density distribution of ion density measured by the double probe configuration

由图9可知，各测点离子密度的概率分布存在显著差异，这很可能是由于尾喷流具有强瞬态、强湍流和高度非线性耦合的特点，呈现出燃烧及电离反应、激波、膨胀波、湍流漩涡、流动分离、边界层分离等多尺度、多物理场耦合共存的复杂流场结构。因此为进一步给出尾焰流场的电导率在全场空间的分布特性，需要着重说明尾焰反应流场结构，并阐明电导率分布与尾焰反应流场结构的相关性。

2.4 朗缪尔双探针离子密度的自相关函数

时间自相关函数表征了随机过程在时间上的相似性。自相关系数为

其中，C(τ)=＜f(t)f(t+τ)＞，C(0)=＜f2(t)＞，f(t)为离子密度测量值。

根据稳态随机过程理论，由时间自相关系数可以定义两种流动时间尺度［18］：积分尺度和泰勒微尺度，定义式分别为

式中Tint为积分尺度；λτ为泰勒微尺度。

为了初步阐明电导率分布与尾焰反应流场结构的相关性，将离子密度数值脉动作为独立随机变量，进而计算各测点离子密度的自相关函数，如图10所示。按照式（13）可计算出按照离子密度自相关系数定义的泰勒时间尺度均在毫秒级。因此，在后续数值计算研究中应重点关注毫秒级泰勒时间尺度的尾焰反应流场结构。

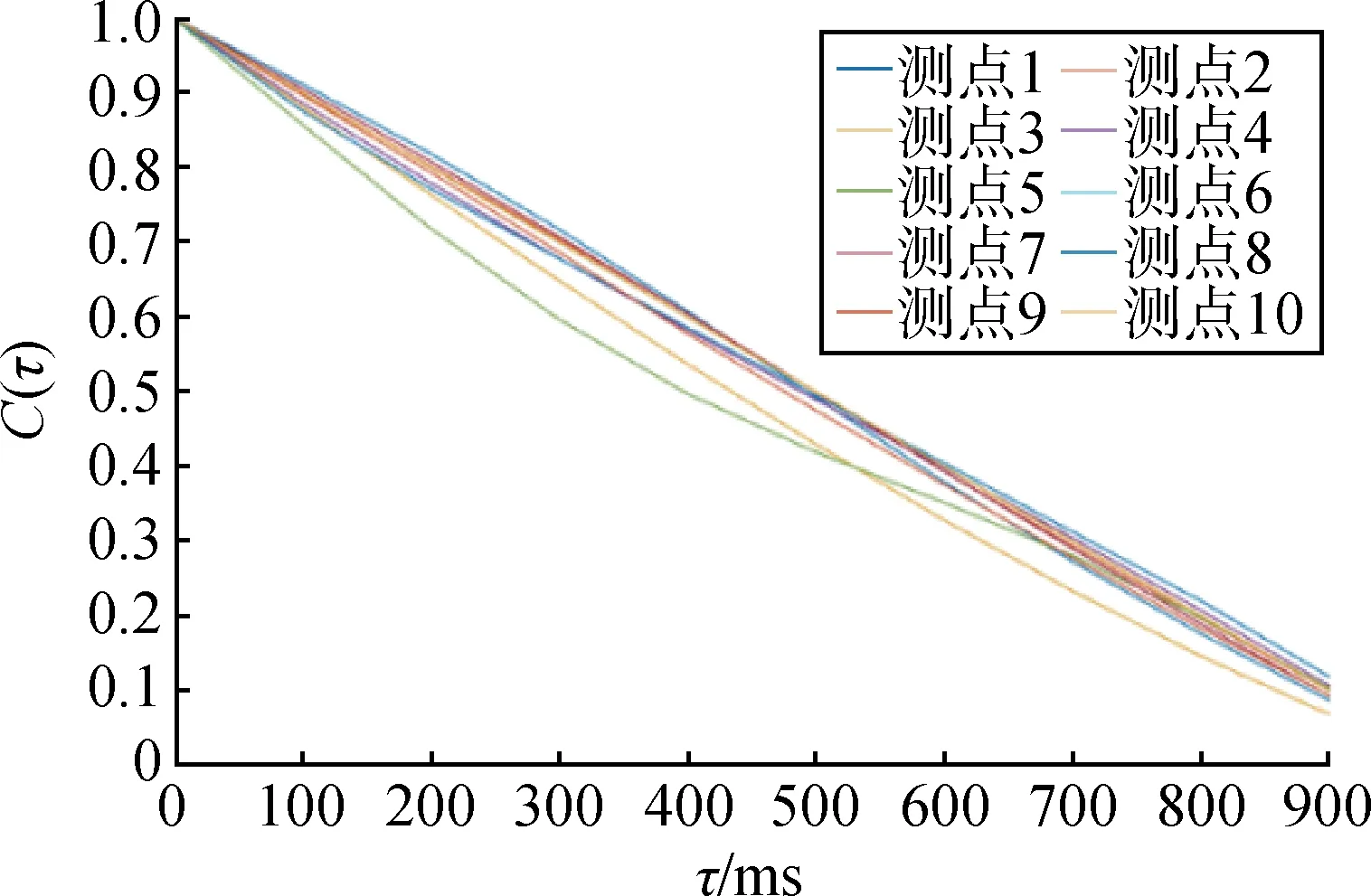
图10 各测点自相关函数Fig.10 Autocorrelation function of each measuring point

2.5 三探针电流的功率谱密度

双探针采样频率仅为10 Hz，无法有效捕捉数值脉动的高频区域，而三探针的采样频率为1 MHz，可以涵盖较高频率的脉动信息。将时域信号通过傅里叶变换到频域来考察脉动信号的频谱特征，图11 为测点1和测点10处探针电流数值的功率谱密度。

图11 电流功率谱密度Fig.11 Power spectral density of current probe

由图11可知，上、下游测点均可观察到50 Hz低频主峰、2 000 Hz以及20 000 Hz高频主峰。低频及高频主峰可能对相应频段电磁信号产生干扰，需要进一步开展数值计算说明尾焰反应流场结构以及电磁振荡特性产生机制。

3 结论

本文针对缩比火箭发动机开展尾焰等离子体特性研究。首先对试验发动机尾焰流场进行了被动自发光谱测量，其次基于朗缪尔双探针和三探针对试验缩比火箭发动机尾焰电导率进行了测量。得到以下结论：

a）缩比火箭发动机尾焰流场被动自发光谱测量存在4个稳定的特征峰，分别对应Na、Fe、Al、C元素，其中Na、Fe、Al 碱金属元素对电导率有突出贡献，碱金属元素分别主要来源于大气中含盐成分、合金结构材料以及推进剂燃烧。

b）朗缪尔双探针测量缩比试验样机电导率约为10-4～10-3S/m，朗缪尔三探针测量电导率约为10-5～10-4S/m，测量差异首先由朗缪尔双探针和朗缪尔三探针的安装位置导致，体现了电导率沿径向分布衰减的特性；其次，基于等离子体鞘层理论的探针测量原理可能不完全适用于火箭发动机尾焰高速弱电离流场，如果要实现更精确的测量，需要对传统探针鞘层理论进行修正。

c）沿该缩比试验发动机样机轴向，朗缪尔双探针、三探针测量电导率均呈指数衰减规律；电导率在上游靠近喷口测量点位呈上升趋势对应发动机建立稳定工作压力的过程。

d）各测点离子密度概率分布存在显著差异，按照离子密度自相关系数定义的泰勒时间尺度均在毫秒级。因此，在后续研究中可重点关注毫秒级泰勒时间尺度的尾焰反应流场结构。

e）上下游测点均可观察到50 Hz 低频主峰、2 000 Hz以及20 000 Hz高频主峰。低频及高频主峰可能对相应频段电磁信号产生干扰，需要进一步开展研究说明尾焰反应流场结构以及电磁振荡特性产生机制。